Transform

2D Transform

Scale

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}s& 0\\ 0& s\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

Reflection

Shear

水平方向的偏移量是和y有关的线性函数，在y = 0的时候，偏移量为0，在y = 1的时候，偏移量为a，得出$$偏移量=ay$$

而$$x^{\prime }=x+偏移量=x+ay$$，转换到矩阵表达式就是在一行二列的位置设a
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& a\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

分析变换的思路：找到变换前后坐标轴的关系

Rotate

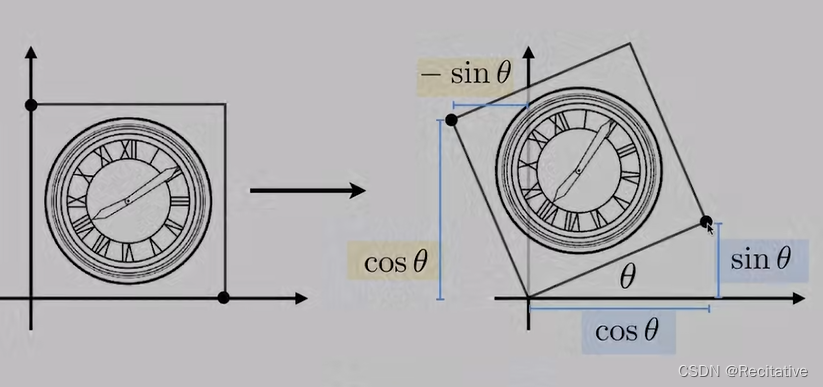
不具体指明的话，旋转默认指围绕原点，逆时针方向。

$$R_{\theta }=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$
推导逻辑：因为任意点都满足旋转公式，则特殊点(1,0)(0,1)也满足该条件。

这个性质3棕1蓝做过说明：在线性变换后，网格线保持平行且等距分布。

写出原始公式
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$
带入特殊点
$$\begin{gathered} \left[\begin{array}{c}\cos \theta \\ \sin \theta \end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}1\\ 0\end{array}\right]\to \{\begin{array}{c}A=\cos \theta \\ C=\sin \theta \end{array} \\ \left[\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}0\\ 1\end{array}\right]\to \{\begin{array}{c}B=-\sin \theta \\ D=\cos \theta \end{array} \end{gathered}$$

如果想要旋转$$-\theta$$角度，则：
$$R_{-\theta }=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]=R_{\theta }^T=R_{\theta }^{-1}$$
即旋转矩阵是一个正交矩阵，根据这个性质，当需要旋转相反角度的时候，可以直接用矩阵的转置来变换。

正交矩阵补充

对于一个矩阵M，如果其转置M^T满足
$$M{M}^T=M^{T}M=I$$
则称该矩阵为正交矩阵。同时，根据矩阵逆的性质$$M{M}^{-1}=M^{-1}M=I$$，可知对正交矩阵，其转置M^T和逆M^-1相等。

正交矩阵转置和逆相等的性质非常有用，可以省去求逆的大量计算，用简单的转置操作求逆矩阵。

判断一个方阵是否为正交矩阵：

对矩阵
$$M=[\mathbf{a},\mathbf{b},\mathbf{c}{]}^T$$
其与转置$$M^T=[\mathbf{a},\mathbf{b},\mathbf{c}]$$的乘积为：
$$\begin{gathered} M{M}^T=\left[\begin{array}{c}\mathbf{a}\\ \mathbf{b}\\ \mathbf{c}\end{array}\right]\left[\mathbf{a},\mathbf{b},\mathbf{c}\right]= \\ \left[\begin{array}{ccc}a\cdot a& a\cdot b& a\cdot c\\ b\cdot a& b\cdot b& b\cdot c\\ c\cdot a& c\cdot b& c\cdot c\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right] \end{gathered}$$
则有下面两条结论：

• 如果一个矩阵是正交矩阵，则矩阵的每个行向量的自点积都为1，即矩阵的每个行向量都是单位矢量.
• 如果一个矩阵是正交矩阵，则矩阵的行向量相互之间的点积为0，即矩阵的行向量相互垂直。

满足这两条的矩阵就是正交矩阵。

Linear Transforms总结

上面所有的变换都可以写成线性表达式，这种变换称为线性变换
$$\begin{gathered} \{\begin{array}{c}{x}^{\prime }=ax+by\\ y^{\prime }=cx+dy\end{array} \\ \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right] \\ {x}^{\prime }=Mx \end{gathered}$$

Homogeneous Coordinate（齐次坐标）

Translation

尝试写成矩阵形式：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$
能够看出来，Translation不是一种线性变换，这种变换称为Affine Map，仿射变换。且线性变换和平移的顺序是，先进行线性变换，再进行平移。

为了避免将Translation当作特例处理，将所有的变换都描述为同一种表示方式，就引入了齐次坐标（Homogeneous Coordinate），所有的仿射变换都可以写为齐次变换。

Homogeneous Coordinate

给2D的点和向量增加一个维度：

• 2D point = (x, y, 1)^T
• 2D vector = (x, y, 0)^T

第三个维度的取值主要看向量表示的是点还是向量

向量后面用0的原因，首先是为了保护向量，保证平移不变性；其次是为了符合下面的运算：

• vector + vector = vector
• point - point = vector
• point + vector = point
• point + point = ??

对于最后一种运算，齐次坐标的点$$\left(\begin{array}{c}x\\ y\\ w\end{array}\right)$$实际表示的是$$\left(\begin{array}{c}x/w\\ y/w\\ 1\end{array}\right)$$在这种定义下，两点之和为两点的中点。

用增加维度后的向量和矩阵表示Translate
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]$$

综上，得到齐次变换和仿射变换的转换关系
$$\begin{gathered} \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}A& B\\ C& D\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right] \\ \left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}A& B& t_x\\ C& D& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}Ax+By+t_x\\ Cx+Dy+t_y\\ 1\end{array}\right] \end{gathered}$$
这里要注意，只有在表示二维仿射变换的情况下，最后一行才是(0, 0, 1)

其他的一些变换

Inverse Transform

对应数学上的逆矩阵。

Composite Transform

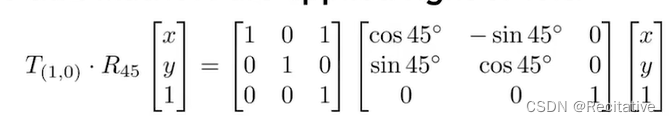
矩阵的乘法，需要从右向左读，因为矩阵乘法不满足交换率，所以不同变换顺序结果不同。

Decomposing Transform

例如想要绕着特定的点c旋转，如下图

因为旋转只能绕原点进行，所以首先要将点移动回原点，然后进行旋转，旋转后再移回去。
$$T(c)\cdot R(\alpha )\cdot T(-c)$$

3D Transform

3维空间也会涉及平移，所以也需要齐次坐标

• 3D point = (x, y, z, 1)^T
• 3D vector = (x, y, z, 0)^T

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{cccc}A& B& C& t_x\\ D& E& F& t_y\\ G& H& I& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$

Scale

$$S(s_x,s_y,s_z)=\left(\begin{array}{cccc}{s}_x& 0& 0& 0\\ 0& s_y& 0& 0\\ 0& 0& s_z& 0\\ 0& 0& 0& 1\end{array}\right)$$

Translation

$$T(t_x,t_y,t_z)=\left(\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right)$$

Rotation

Around x-, y-, or z-axis

$$\begin{gathered} R_x(\alpha )=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \alpha & -\sin \alpha & 0\\ 0& \sin \alpha & \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right) \\ {R}_x(\alpha )=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \sin \alpha & \cos \alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right) \\ {R}_x(\alpha )=\left(\begin{array}{cccc}\cos \alpha & 0& \sin \alpha & 0\\ 0& 1& 0& 0\\ -\sin \alpha & 0& \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right), \\ y是反的原因是，\mathbf{z}\times \mathbf{x}的结果才是+y，而矩阵的顺序是\mathbf{x}\times \mathbf{z}，所以是反过来的 \\ 也可以结合图来推导。 \end{gathered}$$

Compose of R_x, R_y, R_z

$$R_{xyz}(\alpha ,\beta ,\gamma )=R_x(\alpha )R_y(\beta )R_z(\gamma )$$

复杂旋转可以被分解为绕x, y, z轴旋转的方法

使用Rodrigues’ Rotation公式，沿任意轴旋转。

这个公式的结果是一个旋转矩阵，这个矩阵和一个轴n与角度α相关。轴n是默认过原点的，如果想沿着任意起点，可以先translate，再rotation，最后translate回去。

有关最后面的反称矩阵，上一章线性代数，补充了反称矩阵的内容

Viewing Transformation

View / Camera Transformation 视图变换

从模型到图像的过程可以简化为：Model > View > Projection，也就是MVP矩阵

首先要定义相机属性：

• Position $$\mathbf{e}$$
• Look-at / gaze direction $$\hat{g}$$
• Up direction $$\hat{t}$$

将空间中相机的变换和物体的变换，简化为相机固定（位置原点，沿-z看，y轴向上），其他物体变换；

那么首先需要变换相机，使用下面的M_view

• Translate e to origin
• Rotates g to -z
• Rotates t to y
• Rotates (g x t) to x

$$\begin{gathered} M_{view}=R_{view}{T}_{view} \\ {T}_{view}=\left[\begin{array}{cccc}1& 0& 0& -x_e\\ 0& 1& 0& -y_e\\ 0& 0& 1& -z_e\\ 0& 0& 0& 1\end{array}\right] \\ 虽然正向的R_{view}，即g\to -z,t\to y,(g\times t)\to x不是很好写。 \\ 但是其逆矩阵易于求得，即x\to (g\times t),y\to t,z\to -g，易求得： \\ {R}_{view}^{-1}=\left[\begin{array}{cccc}{x}_{g\times t}& x_t& x_{-g}& 0\\ y_{g\times t}& y_t& y_{-g}& 0\\ z_{g\times t}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right] \\ 旋转矩阵满足正交矩阵的条件，因此R_{view}^{-1}=R_{view}^T，故有 \\ {R}_{view}=\left[\begin{array}{cccc}{x}_{g\times t}& y_{g\times t}& z_{g\times t}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right] \end{gathered}$$

Projection

投影是3D到2D的过程，存在两种不同的投影方式：Orthographic和Perspective（正交和透视）。

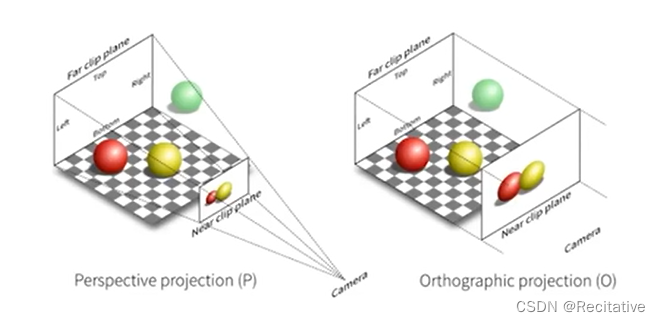
正交投影不会近大远小，而透视投影会。

Orthographic Projection

通俗的来理解，正交投影就是：

• 相机位于原点，看向z轴负向，相机上方为y轴正向
• 抛弃z坐标（从而压扁成一张图像）
• 将结果缩放到[-1,1]²的矩形上

缩放的目的是方便后续操作，例如裁剪和屏幕映射。

在实际的实现过程中，通常为：

• 将空间中的立方体[l, r] x [b, t] x [f, n]，映射到标准立方体（Canonical Cube)[-1, 1]³

  因为看向负z，所以f（远far）要比n（近near）的值小（这是右手系需要注意的问题）。

  OpenGL采用的左手系可以避免，但会产生其他问题

  这个被标准化的立方体是用户自己定义的，也叫Axis-aligned bounding box, AABB，轴对称包围盒，AABB box的面法线与标准基重叠。。

• 第一步，中心移到原点
  $$M_{Translate}=\left[\begin{array}{cccc}1& 0& 0& -\frac{l+r}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

• 第二步，映射到标准立方体(边长为2)
  $$M_{Scale}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]$$

• 合并
  $$\begin{gathered} M_{Ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{l+r}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right] \\ =\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& -\frac{l+r}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{array}\right] \end{gathered}$$

Perspective Projection

使用最广泛的投影，具有近大远小的性质；在视觉上表现为平行线不再平行，而是交于一点。

首先重新强调下齐次坐标中的一条性质（有用）：

• 在齐次坐标下，(x, y, z, 1), (kx, ky, kz, k)(k !=0), (xz, yz, z², z)(z !=0)都表示同一个点(x, y, z)

如何进行透视投影？

• 首先将锥体压成一个立方体（M_persp to M_ortho），有一些规定（使得压缩后结果唯一）：
  • 近平面永远不变
  • 远平面z值不变，只在平面内收缩（注意只是远平面z不变，意味着除了近远平面z都可能变）
  • 远平面中心点挤压后还是中心点。
• 做正交投影（上一节的内容）

x, y行

如图，点(x’, y’, z’)是近平面的点（近平面的点永远不变），以该点为参照，考虑对远平面的点(x, y, z)进行变换

已知变换后的z值不变，y在变换后与y’等高，两者关系根据相似三角形可以推得：
$$y^{\prime }=\frac{n}{z}y$$

该式反映了任意一点的y值如何被挤压成与近平面一致，x值亦同理。

用矩阵来表示的话：
$$\begin{gathered} M_{persp\to ortho}^{4\times 4}\left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}\frac{n}{z}x\\ \frac{n}{z}y\\ unknown\\ 1\end{array}\right) \\ 因为同乘一个非0值，仍然表示同一个点，所以可以同乘z（为了简化计算），则 \\ 上式=\left(\begin{array}{c}nx\\ ny\\ unknown\\ z\end{array}\right) \end{gathered}$$
从而可以部分推得变换矩阵：
$$M_{persp\to ortho}^{4\times 4}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ ?& ?& ?& ?\\ 0& 0& 1& 0\end{array}\right]$$

z行

接着推导z的变换。已知：

• 近平面的点不会变化
• 远平面点的z值不变，远平面中心点不变

开始带入特殊点。设近平面一点(x, y, n, 1)，对其进行变换：
$$M_{persp\to ortho}^{4\times 4}\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)=\left(\begin{array}{c}x\\ y\\ n\\ 1\end{array}\right)==\left(\begin{array}{c}nx\\ ny\\ n^2\\ n\end{array}\right)$$
可以注意到z值变换与x, y无关，则变换矩阵的第三行应该是类似(0 0 A B)的形式。

同理，设远平面中心点(0, 0, f, 1)，进行变换
$$M_{persp\to ortho}^{4\times 4}\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)=\left(\begin{array}{c}0\\ 0\\ f\\ 1\end{array}\right)==\left(\begin{array}{c}0\\ 0\\ f^2\\ f\end{array}\right)$$
可得
$$\begin{gathered} \{\begin{array}{c}An+B=n^2\\ Af+B=f^2\end{array} \\ \to \{\begin{array}{c}A=n+f\\ B=-nf\end{array} \\ {M}_{persp\to ortho}^{4\times 4}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right] \end{gathered}$$

从而推得透视变换的矩阵为：
$$\begin{gathered} M_{Presp}=M_{Ortho}{M}_{Presp\to Ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& -\frac{l+r}{r-l}\\ 0& \frac{2}{t-b}& 0& -\frac{t+b}{t-b}\\ 0& 0& \frac{2}{n-f}& -\frac{n+f}{n-f}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right] \\ =\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& -\frac{l+r}{r-l}& 0\\ 0& \frac{2n}{t-b}& -\frac{t+b}{t-b}& 0\\ 0& 0& \frac{n+f}{n-f}& -\frac{2nf}{n-f}\\ 0& 0& 1& 0\end{array}\right] \end{gathered}$$

Question

对于除了远近平面外任意一个点，在变换后，其z值是否会发生变化？

换句话说，以$$z=\frac{n+f}{2}$$为例，该点在变换后，会被推向近平面还是远平面？

摘自RTR4：One effect of using a perspective transormation is that the computed depth value does not vary linearly with the input p_z value. Using any of Equations to multiply with a point $$\mathbf{p}$$, we can see that
$$\begin{gathered} v=M_{Persp}p=\left(\begin{array}{c}...\\ ...\\ A{p}_z+B\\ \pm p_z\end{array}\right)=\left(\begin{array}{c}...\\ ...\\ \frac{A{p}_z+B}{p_z}\\ \pm 1\end{array}\right) \\ 以上面推导的公式为例，A=\frac{n+f}{n-f},B=-\frac{2nf}{n-f} \end{gathered}$$
可以看出来，z值变化和近远平面的位置有关（Placement of the near and far planes affects the precision of z-buffer）

从上图（同样摘自RTR4）上来看，最终的z值都偏大，即被推向远平面？

进一步思考，近平面离原点越远，透视视体越接近正交视体的形状，在图中表现为，随着近平面距离的增加，曲线越来越接近对角线，且该趋势是单向的，所以z值应当是始终被推向远平面。

透视投影视体的推导

• 变换为正交投影的矩阵，只需要近远平面的z值（即zNear和zFar）。
• 正交投影的变换矩阵，需要定义l, r, b, t（根据视锥体的fov和aspect ratio计算）。

转换为l, r, b, t（近平面的）

• 计算b, t：通过fovY / 2夹角的三角关系。$$\tan \frac{fovY}{2}=\frac{t}{|n|}$$
  $$b=-t$$
• 计算l, r：$$aspectratio=\frac{r}{t}$$

Screen Mapping

将标准立方体的宽度和高度拉伸到屏幕的width和height，z值暂时不处理。

• 标准立方体的边长为2，所以缩放要先除2
  $$\left[\begin{array}{cccc}\frac{width}{2}& 0& 0& 0\\ 0& \frac{height}{2}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

• 还需要对其原点位置，例如以左下角为原点
  $$\left[\begin{array}{cccc}\frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

参考

• GAMES101
• 3blue1brown-线性代数的本质
• 《Unity Shader入门精要》
• 《Real Time Rendering 4th Edition》