Make Decision

Machine learning diagnostic

这里的diagnostic指的是通过一系列测试，了解什么手段对提升模型性能有效，比如决定是否需要花费时间来收集新的数据。

一些常用的提升性能的方法包括：

• 增加数据
• 调整特征
• 调整正则项

Evaluation

在正式开始前，首先来看看如何评估一个模型的好坏

test set

首先可以考虑的方法是划分一部分数据出来作为测试集，在训练集上训练，在测试集中验证模型的性能。常见的划分比例为7：3.

可以使用scikit-learn的sklearn.model_selection.train_test_split，。将数据集划分为train和test两部分

X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33, random_state=1)

以此前的房价预测模型为例，该例子使用linear regression，在训练过程中，仍然最小化损失函数
$$J(\vec{w},b)=\underset{\vec{w},b}{\min }[\frac{1}{2m_{train}}\sum _{i=1}^{m_{train}}(f_{\vec{w},b}(\vec{x})-y{)}^2+\frac{\lambda }{2m_{train}}\sum _{j=1}^n{w}_j^2]$$

并根据在训练集和测试集上的error评估模型，注意这里没有正则项。
$$\begin{gathered} J_{test}(\vec{w},b)=\frac{1}{2m_{test}}[\sum _{i=1}^{m_{test}}(f_{\vec{w},b}({\vec{x}}_{test})-y_{test}{)}^2] \\ {J}_{train}(\vec{w},b)=\frac{1}{2m_{train}}[\sum _{i=1}^{m_{train}}(f_{\vec{w},b}({\vec{x}}_{train})-y_{train}{)}^2] \end{gathered}$$

类似的，对于logistic regression，error可以是
$$\begin{gathered} J_{test}(\vec{w},b)=-\frac{1}{m_{test}}\sum [y_{test}\log (f_{\vec{w},b}({\vec{x}}_{test}))+(1-y_{test}\log (1-f_{\vec{w},b}({\vec{x}}_{test}))] \\ {J}_{train}(\vec{w},b)=-\frac{1}{m_{train}}\sum [y_{train}\log (f_{\vec{w},b}({\vec{x}}_{train}))+(1-y_{train}\log (1-f_{\vec{w},b}({\vec{x}}_{train}))] \end{gathered}$$

不过对分类问题，更常用的是评估有没有分类对

• $J_{test}(\vec{w},b)$为test集中分类错误的比率
• $J_{train}(\vec{w},b)$为train集中分类错误的比率

Model selection

首先用一个简单的例子，理解如何选择合适的模型，假设存在一系列线性回归模型，分别计算出$J_{test}$

我们希望模型能够在新的数据上表现得也很不错，因此应该选择$J_{test}$最小的；

下图是一个过拟合的示例，由于数据过度拟合训练集，导致其在测试集上的表现不佳。

Cross validation

在前面介绍的方法中，我们首先将模型划分为训练集和测试集，然后对不同的模型，求其在测试集上的误差$j_{test}$；现在来进一步改进这个方法：

首先将数据集划分为三个（而不是两个）部分，分别是训练集、交叉验证（cross validation）集和测试集

同样可以使用train_test_split方法，划分两次

X_train, X_, y_train, y_ = train_test_split(X,y,test_size=0.40, random_state=1)
X_cv, X_test, y_cv, y_test = train_test_split(X_,y_,test_size=0.50, random_state=1)

cross validation用来测试（check）模型的有效性（validity）或真实性（accuracy），也有人简称validation set，或者叫development set、dev set。

在每个数据集上计算error
$$\begin{array}{l}{J}_{test}(\vec{w},b)=\frac{1}{2m_{test}}[{\sum }_{i=1}^{m_{test}}(f_{\vec{w},b}({\vec{x}}_{test})-y_{test}{)}^2]\\ J_{cv}(\vec{w},b)=\frac{1}{2m_{cv}}[{\sum }_{i=1}^{m_{cv}}(f_{\vec{w},b}({\vec{x}}_{cv})-y_{cv}{)}^2]\\ J_{train}(\vec{w},b)=\frac{1}{2m_{train}}[{\sum }_{i=1}^{m_{train}}(f_{\vec{w},b}({\vec{x}}_{train})-y_{train}{)}^2]\end{array}$$

使用这三个数据集来选择合适的模型，首先计算$J_{cv}$

选择$J_{cv}$最小的模型。最后再用$J_{test}$评估模型的泛化性能。这个过程可以用代码自动完成。

一种直观的理解方式为：train set拟合了多组模型参数，dev set从这些组中选择了在dev set上表现最好的那一组，被选择的模型已经见过train和dev中的数据了，不适合用来评估模型的泛化能力；而此时test中的数据都是模型没有见过的，因此可以用test中的数据来评估泛化能力。

总结一下，在模型选择阶段，我们只使用train set和dev set；只有在选择了模型只有，我们才会使用test set来评估模型的性能。

$J_{cv}$通常会比$J_{train}$大，因为模型是在train set上训练的，通常会更拟合train set，在dev set上的表现会差一些。

Bias and Variances

在线性回归部分，我们曾讨论过模型的不同拟合情况，可以被描述为欠拟合（underfit，High bias），过拟合（overfit, High variance）或者Just right。试着用$J_{train}$和$J_{cv}$来衡量拟合情况。

• 对欠拟合的情况，由于模型不能很好地拟合train set，因此$J_{train}$一定很高；同理在$J_{cv}$上的表现也不会很好
• 对过拟合的情况，模型在train set表现的很好，$J_{train}$较低；但在新的数据上表现不佳，$J_{cv}$很高

以多项式的阶数d为横轴，$J$为纵轴绘制$J_{train}$和$J_{cv}$的曲线，直觉上，$J_{train}$会随着d的增加不断降低；而$J_{cv}$会随着d的增加，呈倒钟形，如下图所示

由此判断模型是否存在bias和variance问题

• High bias：High $J_{train}$，$J_{cv}\approx J_{train}$
• High variance：$J_{cv}\gg J_{train}$
• High bias & High variance：线性模型通常不会有，但神经网络会出现，High $J_{train}$，$J_{cv}\gg J_{train}$

第三种情况代表模型对某些输入过拟合，但对另外一些输入又欠拟合

对bias-variance problem再做些说明：

• bias error是由于学习算法的假设错误（erroneous assumption）导致的误差，直观理解就是算法没有学习到feature和label之间的关联，表现为欠拟合；
• variance 反应了模型对训练集中微小变化的灵敏度。微小变化可以理解为噪声（noise），用来衡量模型是否过度拟合

可以根据图更直观观察，

两者其实可以类比准确度(accuracy)和精确度(precision)之间的关系：准确度反映了bias，高准确度对应低bias；而精确度反映了variance，高精确度对应低variance

下图是练习lab中绘制的不同degree下的拟合关系。可以更清晰地观察如何选择合适的模型

Regularization and bias/variance

正则化方法同样会影响bias/variance，可以依据两者的关系选择合适的$\lambda$。

直观上理解，当$\lambda$很高的时候，正则项的比重较大，模型不易拟合（更加平滑），且参数逼近0；当$\lambda$很低的时候（例如0），正则项比较不足，模型易过拟合。

选择$\lambda$的过程和选择model的过程类似，选择一系列模型中$J_{cv}$最小那个，并在test集上测试，得到$J_{test}$

下图是在degree = 10的情况下，应用不同量级的正则化获得的模型图像，可以更直观观察正则化对模型的影响

Establishing a baseline level of performance

通过一些具体的数字，来学习如何判断$J$是过高还是过低。

以语音识别任务为例，假设得到了一个模型，$J_{train}=10.8\%$，$J_{cv}=14.8\%$，单从这两个数字来看，似乎无法判别模型到底好还是坏。此时可以引入实际场景中，人类对该任务的表现能力

如图所示，人类在该语音识别任务中的表现能力为$10.6\%$，以这个数值为baseline，模型在训练集上表现得非常不错，相比之下，在验证集上的表现就差一些。因此variance问题要比bias问题大些。

从上图也可以观察到，bias反映了$J_{train}$和beseline的差距，而variance反映了$J_{train}$与$J_{cv}$的差异

建立baseline即意味着建立对该任务能够接受的合理误差范围，常用的baseline参考包括：

• 人类在该任务上的水平
• 其他已有算法的水平
• 根据以往的经验

Learning Curve

当模型表现不好的时候，我们有时会采取增加数据的方式来提高模型性能。在实际开始增加数据之前，有必要判断增加数据的有效性。

可以通过绘制m（train set size）-J（error）曲线，观察$J_{train}$和$J_{cv}$来帮助判断。

如上图所示，在High bias的情况下，模型的假设验证误差不会随着数据的增多而降低。此时比起增加数据，应该考虑其他的方法来优化模型。

$J_{train}$上升是因为随着数据的增加，模型会越来越难拟合数据，而曲线逐渐变平则是由于，随着数据量的增加，数据点会更加反映出真实分布的规律，使得误差更加接近真实分布与假设分布的实际差异。

$J_{cv}$下降是因为随着数据的增加，train set与dev set的差异性会不断减小，使得两者的误差更加接近。

而在High variance的情况下，模型的性能能够随着数据的增加变好，可以通过增加数据的方式来优化模型。

另一种理解方式为，variance反映了对数据采样过程中的随机噪声，即数据集分布与真实分布之间的差异，通过增加数据可以降低该差异，从而提升模型性能。

在实际实践中，可以尝试划分不同大小的数据集自己分别进行测试，绘制类似上面的曲线的方式，来判断是否需要进一步增加数据来提升模型性能。

Debugging

回到最开始的问题，假设房价预测的线性模型
$$J(\vec{w},b)=\underset{\vec{w},b}{\min }[\frac{1}{2m_{train}}\sum _{i=1}^{m_{train}}(f_{\vec{w},b}(\vec{x})-y{)}^2+\frac{\lambda }{2m_{train}}\sum _{j=1}^n{w}_j^2]$$
表现出了高误差，应该如何提升模型性能？根据前面讨论的内容，可以对方法进行分类：

• fix high variance
  • 更多数据
  • 减少特征
  • 增大$\lambda$
• fix high bias
  • 增加特征
  • 设计多项式特征
  • 减小$\lambda$

Applied to Neural Network

大型的神经网络通常都可以很好地拟合训练集，意味着只要神经网络足够大，就可以获得low bias的模型。

因此，在可以获取足够数据的情况下， 可以考虑下图的开发流程，获得具有良好表现的神经网络

首先，检查$J_{train}$，若模型的bias过高，就增大神经网络，直到获得合适大小的网络；然后，检查$J_{cv}$，如果variance过高，就尝试增加数据。在这个过程中，可能随时会出现bias过高或者variance过高，根据实际的情况，选择对应的策略即可。

不断增大模型，这可能会导致两个问题。首先是过度拟合，这个问题可以通过选择合适的正则化方法解决，合理正则化后的模型至少和小模型的效果一样好，甚至更好；第二个是算力，大模型往往需要更多的算力支持，且运行时间更长。

在TensorFlow中，调用正则化的只需要在层定义中增加kernel_regularizer=L2(0.01))，就可以引入L2范数正则化。

model = Sequential([
	Dense(25, activation = 'relu', kernal_regularizer=L2(0.01)),
    Dense(15, activation = 'relu', kernal_regularizer=L2(0.01)),
    Dense(1, activation = 'sigmoid', kernal_regularizer=L2(0.01))
])

正则化方法包含三个关键字：

• kernel_regularizer，对层kernel的weights matrix添加惩罚
• bias_regularizer，对层的bias vector添加惩罚
• activity_regularizer，对层的输出添加乘法。

前两个的差别在于，一个针对权重矩阵做正则化，另一个针对偏移向量做正则化。可以选择的惩罚项包含L1, L2和L1L2。也支持自己设计。

Implements

举一个分类的例子，假设要对下面的数据进行分类，右图是假想的边界线

loss用错误率来表示，编写代码

def eval_cat_err(y, yhat):
    """ 
    Calculate the categorization error
    Args:
      y    : (ndarray  Shape (m,) or (m,1))  target value of each example
      yhat : (ndarray  Shape (m,) or (m,1))  predicted value of each example
    Returns:|
      cerr: (scalar)             
    """
    
    icorrect = (y != yhat)
    cerr = icorrect.mean()
    
    return(cerr)

先试着使用一个非常大的模型（肯定会过拟合），

tf.random.set_seed(1234)
model = Sequential(
    [
        ### START CODE HERE ### 
        Dense(120, activation = 'relu'),
        Dense(40, activation = 'relu'),
        Dense(6, activation = 'linear')
        ### END CODE HERE ### 

    ], name="Complex"
)
model.compile(
    ### START CODE HERE ### 
    loss= SparseCategoricalCrossentropy(from_logits=True),
    optimizer= tf.keras.optimizers.Adam(0.01),
    ### END CODE HERE ### 
)

训练该模型后，绘制边界线，很明显模型出现了过拟合。

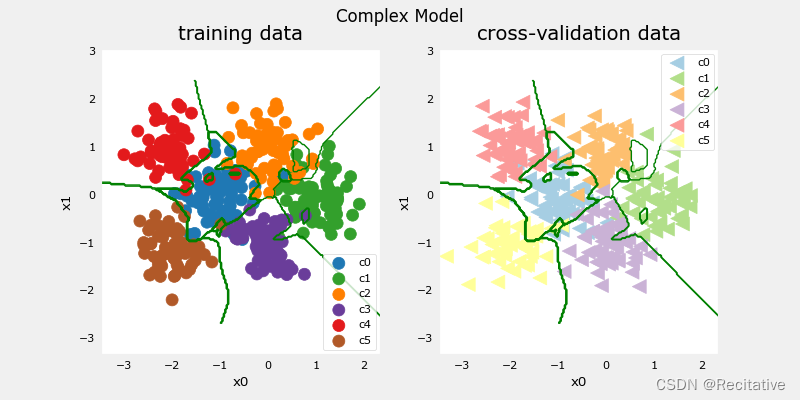
测试一个更简单的模型

tf.random.set_seed(1234)
model_s = Sequential(
    [
        ### START CODE HERE ### 
        Dense(6, activation = 'relu', name = 'L1'),
        Dense(6, activation = 'linear', name = 'Output')
        ### END CODE HERE ### 
    ], name = "Simple"
)
model_s.compile(
    ### START CODE HERE ### 
    loss=SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(0.01),
    ### START CODE HERE ### 
)

比较两个模型的error

categorization error, training, simple model, 0.070, complex model: 0.005
categorization error, cv,       simple model, 0.072, complex model: 0.100

从结果中可以观察到，简单的模型虽然在训练集上表现不如复杂模型，但表现出了更好的泛化能力。

Regularization

对复杂模型的隐层应用正则化

tf.random.set_seed(1234)
model_r = Sequential(
    [
        ### START CODE HERE ### 
        Dense(120, activation = 'relu', kernel_regularizer=tf.keras.regularizers.l2(0.1)),
        Dense(40, activation='relu', kernel_regularizer=tf.keras.regularizers.l2(0.1)),
        Dense(6, activation='linear')
        ### START CODE HERE ### 
    ], name= None
)
model_r.compile(
    ### START CODE HERE ### 
    loss=SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(0.01),
    ### START CODE HERE ### 
)

categorization error, training, regularized: 0.075, simple model, 0.070, complex model: 0.033
categorization error, cv,       regularized: 0.062, simple model, 0.059, complex model: 0.125

正则化之后，模型在训练集上的表现下降，但在验证集上的表现变好了。

Iterate to fime optimal lambda

通过迭代寻找一组$\lambda$中最合适的那个

tf.random.set_seed(1234)
lambdas = [0.0, 0.001, 0.01, 0.05, 0.1, 0.2, 0.3]
models=[None] * len(lambdas) # 好像是一种广播方法，这里用来广播到len长度
for i in range(len(lambdas)):
    lambda_ = lambdas[i]
    models[i] =  Sequential(
        [
            Dense(120, activation = 'relu', kernel_regularizer=tf.keras.regularizers.l2(lambda_)),
            Dense(40, activation = 'relu', kernel_regularizer=tf.keras.regularizers.l2(lambda_)),
            Dense(classes, activation = 'linear')
        ]
    )
    models[i].compile(
        loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
        optimizer=tf.keras.optimizers.Adam(0.01),
    )

    models[i].fit(
        X_train,y_train,
        epochs=1000
    )
    print(f"Finished lambda = {lambda_}")

参考

• 吴恩达《机器学习2022》
• 西瓜书
• tensorflow.org