有穷自动机
有穷自动机(finite automaton)是最简单的计算模型(computational model),又叫有穷状态机(finite state machine);对应马尔科夫链(Markov chain)。这种计算机模型的描述能力和资源极其有限,但却可以完成很多工作。
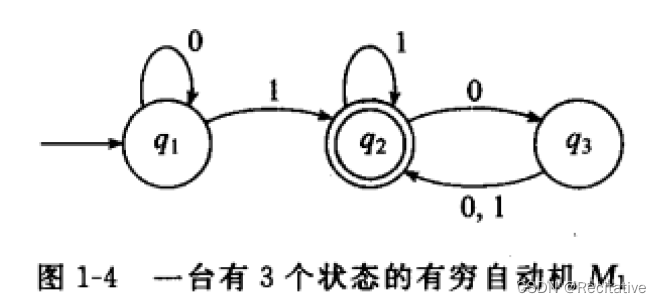
从直觉上定义一个有穷自动机的话,可以理解为一个拥有初始状态 q 0 q_0 q0的机器,会根据有限种可能的输入,在特定规则下不断改变自己的状态,最终停留在某个/多个中的一个输出/终止状态的计算机。我们可以用一张状态图(state diagram)来表述这样一个有穷自动机。
严格定义上,有穷状态机包含以下5个部分:
- 状态集(state set) Q Q Q,包含有限种可能的状态
- 字母表(alphabet) Σ \Sigma Σ,包含所有可能的输入符号
- 转移函数(transition function) δ \delta δ,描述从任意属于 Q Q Q的状态,经 Σ \Sigma Σ中的输入,映射到 Q Q Q中任意状态的函数,可以用转移表(transition table)来描述,记 Q × Σ → Q Q \times \Sigma \to Q Q×Σ→Q
- 起始状态(start state) q 0 ∈ Q q_0 \in Q q0∈Q
- 接受状态集(accept state set),又称终止状态集(final state set) F ⊆ Q F \subseteq Q F⊆Q,包含一系列可行的终止状态
即,我们可以使用5元组 ( Q , Σ , δ , q 0 , F ) (Q, \Sigma, \delta, q_0, F) (Q,Σ,δ,q0,F)来描述一个有穷自动机。以上面的状态图为例,其5元组为:
- Q = { q 1 , q 2 , q 3 } Q = \{q1, q2, q3\} Q={q1,q2,q3}
- Σ = { 0 , 1 } \Sigma = \{0, 1\} Σ={0,1}
- δ = 0 1 q 1 q 1 q 2 q 2 q 3 q 2 q 3 q 2 q 2 \begin{array}{}\delta = & \begin{array}{c|cc} &0&1\\ \hline q_1 & q_1 & q_2\\ q_2&q_3&q_2\\ q_3&q_2&q_2\end{array}\end{array} δ=q1q2q30q1q3q21q2q2q2,或表述为,对任意输入 a ∈ Σ a\in \Sigma a∈Σ,存在 δ ( q i , a ) = q i + 1 \delta(q_i, a) = q_{i+1} δ(qi,a)=qi+1
- q 1 q_1 q1
- F = { q 2 } F=\{q_2\} F={q2}
正则语言
设有穷自动机 M = ( Q , Σ , δ , q 0 , F ) M = (Q, \Sigma, \delta, q_0, F) M=(Q,Σ,δ,q0,F), w = w 1 w 2 … w n w = w_1w_2\dots w_n w=w1w2…wn为 Σ \Sigma Σ中字符组成的字符串,若对应的状态序列 r = r 0 , r 1 , … , r n r = r_0, r_1,\dots,r_n r=r0,r1,…,rn满足:
- r 0 = q 0 r_0 = q_0 r0=q0;
- r n ∈ F r_n \in F rn∈F
- δ ( r i , w i + 1 ) = w i + 1 , i = 0 , 1 , … , n − 1 \delta(r_i, w_{i+1}) = w_{i+1}, i=0,1,\dots,n-1 δ(ri,wi+1)=wi+1,i=0,1,…,n−1
则称字符串 w w w能够被机器 M M M接受。
能够被机器
M
M
M接受的全部字符串组成的集合
A
A
A称为该机器的语言(language),记
L
(
M
)
=
A
L(M) = A
L(M)=A。一个机器可以接受多种字符串,但只能有一个语言。有穷自动机对应的语言为正则语言(regular language)。例如,在前一小节给出的自动机示例,其语言可以写作:
{
w
∣
w
至少含一个
1
,且最后一个
1
后面包含偶数个
0
}
\{w|w至少含一个1,且最后一个1后面包含偶数个0\}
{w∣w至少含一个1,且最后一个1后面包含偶数个0}
有穷自动机的设计
设计能够接受对应字符串的有穷自动机,可遵循以下步骤:
- 确定字母表( Σ \Sigma Σ)
- 画出所有可能的状态(Q)
- 标注初始状态,接受状态( q 0 , F q_0, F q0,F)
- 考虑所有状态转移的可能性( δ \delta δ)
非确定性
如果一个计算,其每步都按唯一方式跟随前一步;或者说,如果一个机器,对给定的符号,只有唯一对应的状态转移,则称这种计算为确定型计算(deterministic computation),否则,称非确定型计算(nondeterministic computation)。
确定型有穷自动机(DFA)与非确定型有穷自动机(NFA)存在若干差别:
- DFA对字母表中任意符号只有一个状态转移,而NFA可以对应0个、1个或多个。
- DFA中的符号都来自字母表,而NFA中的符号可以是 ε \varepsilon ε或字母表中的任意字符,记 Σ ∪ { ε } = Σ ε \Sigma \cup \{\varepsilon\} = \Sigma_\varepsilon Σ∪{ε}=Σε
- DFA的计算是线性的,而NFA的计算是树状的,当存在多个转移的时候,NFA会采取分支并行的策略。
每一台NFA都可以转换成等价的DFA,但有些时候构造NFA要比构造等价的DFA简单得多,且需要的状态数更少(更小),更易于理解。
等价性证明
如果两台机器能够识别同样的语言,则称这两台机器等价。
待证:设 N = ( Q , Σ , δ , q 0 , F ) N = (Q, \Sigma, \delta, q_0, F) N=(Q,Σ,δ,q0,F)为识别语言 A A A的NFA,构造等价的DFA
证明:首先定义 P ( Q ) \mathcal P(Q) P(Q)为 Q Q Q中状态的子集组成的集合,即待构造DFA中的一个状态,相当于 Q Q Q中的一个状态子集(如果觉得抽象,可以参考下文正则计算中,并计算的DFA方法证明)。待构造DFA中的状态记为 R ∈ Q ′ R \in Q' R∈Q′。
定义 E ( R ) E(R) E(R)为从 R R R的任意成员出发,可经 ε \varepsilon ε到达的状态集合,即无输入可抵达的状态。构造DFA M = ( Q ′ , Σ , δ ′ , q 0 ′ , F ′ ) M = (Q', \Sigma, \delta', q_0', F') M=(Q′,Σ,δ′,q0′,F′)
- Q ′ = P ( Q ) Q' = \mathcal P(Q) Q′=P(Q)
- Σ = Σ \Sigma = \Sigma Σ=Σ
- ∀ R ∈ Q ′ , a ∈ Σ , 有 δ ′ ( R , a ) = { q ∣ q = δ ( r , a ) 且 q ∈ Q , r ∈ R } \forall R\in Q', a\in \Sigma,有 \delta'(R, a) = \{q|q = \delta(r, a)且q \in Q, r \in R\} ∀R∈Q′,a∈Σ,有δ′(R,a)={q∣q=δ(r,a)且q∈Q,r∈R}
- q 0 ′ = E ( { q 0 } ) q_0' = E(\{q_0\}) q0′=E({q0})
- F ′ = { R ∣ R 包含 N 的一个可接受状态 } F' = \{R|R包含N的一个可接受状态\} F′={R∣R包含N的一个可接受状态}
由该证明可推出,如果一个语言是正则的,当且仅当一个NFA可以接受该语言,因为NFA可以等价为DFA,而每个语言都有一台能够接受它的DFA。
正则计算
简记一下正则运算的证明。主要推导5种:
- 并: A ∪ B = { x ∣ x ∈ A 或 X ∈ B } A \cup B = \{x|x\in A 或 X \in B\} A∪B={x∣x∈A或X∈B}
- 连接: A ∘ B = { x y ∣ x ∈ A 且 x ∈ B } A \circ B = \{xy|x\in A且x\in B\} A∘B={xy∣x∈A且x∈B}
- 星: A ∗ = { x 1 x 2 … x k ∣ k ≥ 0 且 x i ∈ A } A^* = \{x_1x_2\dots x_k|k\ge0且x_i\in A\} A∗={x1x2…xk∣k≥0且xi∈A}
- 补:$\bar A = {x | x\notin A} $
- 交: A ∩ B = { x ∣ x ∈ A 且 x ∈ B } A \cap B = \{x|x\in A且x \in B\} A∩B={x∣x∈A且x∈B}
5种运算全部封闭,即运算的结果也是正则语言。因为是证明能够识别对应语言的机器 ∃ \exist ∃,所以最好用构造性证明。
并
待证:已知语言 A , B A, B A,B是正则语言,证明 A ∪ B A \cup B A∪B为正则语言
证明(DFA):构造满足条件的自动机,其每个状态 r r r都是 A A A和 B B B的状态组成的数对 ( r 1 , r 2 ) (r_1, r_2) (r1,r2)
- Q = { ( r 1 , r 2 ) ∣ r 1 ∈ A 且 r 2 ∈ B } Q = \{(r_1, r_2)|r_1 \in A 且 r_2 \in B\} Q={(r1,r2)∣r1∈A且r2∈B}, Q Q Q相当于集合 Q 1 , Q 2 Q_1, Q_2 Q1,Q2的笛卡尔积,可记为 Q = Q 1 × Q 2 Q = Q_1 \times Q_2 Q=Q1×Q2
- Σ = Σ 1 + Σ 2 \Sigma = \Sigma_1 + \Sigma_2 Σ=Σ1+Σ2
- q = ( q 1 , q 2 ) q = (q_{1}, q_{2}) q=(q1,q2)
- F = { ( r 1 , r 2 ) ∣ r 1 ∈ F 1 或 r 2 ∈ F 2 } F = \{(r_1, r_2) | r_1\in F_1或r_2 \in F_2\} F={(r1,r2)∣r1∈F1或r2∈F2}
- δ ( ( r 1 , i , r 2 , i ) , a ) = ( δ ( r 1 , i , a ) , δ ( r 2 , i , a ) ) = ( r 1 , i + 1 , r 2 , i + 1 ) \delta((r_{1,i}, r_{2,i}),a) = (\delta(r_{1,i}, a), \delta(r_{2,i}, a)) = (r_{1, i+1}, r_{2, i+1}) δ((r1,i,r2,i),a)=(δ(r1,i,a),δ(r2,i,a))=(r1,i+1,r2,i+1)
笛卡尔积的结果,可以理解为两个集合中的元素,所有可能的组合
证明(NFA):
- Q = { q 0 } ∪ Q 1 ∪ Q 2 Q = \{q_0\} \cup Q_1 \cup Q_2 Q={q0}∪Q1∪Q2, q 0 q_0 q0通过 ε \varepsilon ε迁移到 M 1 , M 2 M_1,M_2 M1,M2的初始状态
- Σ = Σ 1 ∪ Σ 2 \Sigma = \Sigma_1 \cup \Sigma_2 Σ=Σ1∪Σ2
- q 0 q_0 q0
- F = F 1 ∪ F 2 F = F_1 \cup F_2 F=F1∪F2
- δ ( q , a ) = { δ 1 ( q , a ) q ∈ Q 1 δ 2 ( q , a ) q ∈ Q 2 { q 1 , q 2 } q = q 0 且 a = ε ∅ q = q 0 且 a ≠ ε \delta(q, a) = \left\{\begin{array}{}\delta_1(q, a) & q \in Q_1\\ \delta_2(q, a) & q \in Q_2\\ \{q_1, q_2\} & q=q_0且a = \varepsilon\\ \empty & q = q_0且a\ne \varepsilon\end{array}\right. δ(q,a)=⎩ ⎨ ⎧δ1(q,a)δ2(q,a){q1,q2}∅q∈Q1q∈Q2q=q0且a=εq=q0且a=ε
连接
待证:正则语言在连接运算下封闭
- Q = Q 1 ∪ Q 2 Q = Q_1 \cup Q_2 Q=Q1∪Q2
- Σ = Σ 1 ∪ Σ 2 \Sigma = \Sigma_1 \cup \Sigma_2 Σ=Σ1∪Σ2
- q 1 q_1 q1
- F = F 2 F = F_2 F=F2
- δ ( q , a ) = { δ 1 ( q , a ) q ∈ Q 1 且 q ∉ F 1 δ 1 ( q , a ) q ∈ F 1 且 a ≠ ε δ 2 ( q , a ) ∪ { q 2 } q ∈ F 1 且 a = ε δ 2 ( q , a ) q ∈ Q 2 \delta(q, a) = \left\{\begin{array}{}\delta_1(q, a) & q \in Q_1且q\notin F_1\\ \delta_1(q, a) & q \in F_1且a \ne \varepsilon\\ \delta_2(q, a) \cup\{q_2\} & q \in F_1且a = \varepsilon\\ \delta_2(q, a) & q \in Q_2\\\end{array}\right. δ(q,a)=⎩ ⎨ ⎧δ1(q,a)δ1(q,a)δ2(q,a)∪{q2}δ2(q,a)q∈Q1且q∈/F1q∈F1且a=εq∈F1且a=εq∈Q2
星
待证:正则语言在星运算下封闭
- Q = Q 1 ∪ { q 0 } Q = Q_1 \cup \{q_0\} Q=Q1∪{q0}
- Σ = Σ 1 \Sigma = \Sigma_1 Σ=Σ1
- q 0 q_0 q0
- F = F 1 ∪ { q 0 } F = F_1 \cup \{q_0\} F=F1∪{q0}
- δ ( q , a ) = { δ 1 ( q , a ) q ∈ Q 1 且 q ∉ F 1 δ 1 ( q , a ) q ∈ F 1 且 a ≠ ε δ 2 ( q , a ) ∪ { q 1 } q ∈ F 1 且 a = ε { q 1 } q ∈ q 0 且 a = ε ∅ q = q 0 且 a ≠ ε \delta(q, a) = \left\{\begin{array}{}\delta_1(q, a) & q \in Q_1且q\notin F_1\\ \delta_1(q, a) & q \in F_1且a \ne \varepsilon\\ \delta_2(q, a) \cup\{q_1\} & q \in F_1且a = \varepsilon\\ \{q_1\} & q \in q_0且a = \varepsilon\\ \empty & q =q_0且a \ne \varepsilon\\\end{array}\right. δ(q,a)=⎩ ⎨ ⎧δ1(q,a)δ1(q,a)δ2(q,a)∪{q1}{q1}∅q∈Q1且q∈/F1q∈F1且a=εq∈F1且a=εq∈q0且a=εq=q0且a=ε
补
待证:已知 N = ( Q , Σ , δ , q 0 , F ) N = (Q, \Sigma, \delta, q_0, F) N=(Q,Σ,δ,q0,F)识别语言A,证明存在机器识别 A ˉ \bar A Aˉ
- Q ′ = P ( Q ) Q' = \mathcal P(Q) Q′=P(Q).
- Σ \Sigma Σ
- q 0 ′ = P ( q ) q_0' = \mathcal P(q) q0′=P(q),因为也可能从 q 0 q_0 q0出发但和N的状态迁移不一致。
- F ′ = P ( q ) F' = \mathcal P(q) F′=P(q),因为任何状态都可能是接受状态
- δ ′ ( R , a ) = { q ∣ q ∉ δ ( r , a ) , q ∈ Q , r ∈ R } \delta'(R, a) = \{q|q \notin \delta(r,a), q\in Q, r\in R\} δ′(R,a)={q∣q∈/δ(r,a),q∈Q,r∈R}
如果不好理解,不妨想象一个可以接受所有 Σ \Sigma Σ中的字符组成的字符串的全连接网络NFA,每层包含对应 Q Q Q中状态的节点,初始状态 q 0 q_0 q0通过 ε \varepsilon ε迁移到隐层1,隐层数量为可能的最大字符长度。
然后从该网络中剔除状态机N对应的连线,就得到 A ˉ \bar A Aˉ机的转移函数。
交
待证:正则语言的交运算是封闭的
证明:已知 A ˉ , A ∪ B \bar A, A\cup B Aˉ,A∪B都是封闭的,则 A ˉ ∪ B ˉ \bar A \cup \bar B Aˉ∪Bˉ封闭,进而得到 ( A ˉ ∪ B ˉ ) ‾ = A ∩ B \overline{(\bar A \cup \bar B)} = A \cap B (Aˉ∪Bˉ)=A∩B封闭。
正则表达式
证明部分不用想太多,关注正则表达式和自动机怎么相互转换即可。
使用正则运算符来构造语言的表达式称为正则表达式,正则表达式的值是语言。
定义:R为正则表达式的条件:
- R = a , a ∈ Σ R = a, a\in \Sigma R=a,a∈Σ
- R = ε R = \varepsilon R=ε
- R = ∅ R = \empty R=∅
- R R R为正则运算的结果:主要是 ∪ , ∘ , ∗ \cup, \circ, * ∪,∘,∗
上面的定义中, R = ε R=\varepsilon R=ε代表只包含空串的语言, R = ∅ R = \empty R=∅代表不包含任何字符串的语言。由该定义可以得到两个恒等式: R ∪ ∅ = R , R ∘ ε = R R\cup\empty = R, R\circ \varepsilon = R R∪∅=R,R∘ε=R
如果省略括号,则运算的优先级为:星、连接、并(最好还是加上括号)
等价性证明
任何正则表达式都能够转换成能够识别对应语言的自动机,反之亦然。
待证:一个语言是正则的,当且仅当可以使用正则表达式描述该语言。
证明:该证明是充要证明,需要证两个方向。
-
如果一个语言可以使用正则表达式描述,则该语言正则(如何将表达式转换成自动机)
考察正则表达式中的各种情况(构造性证明):
-
R = a R = a R=a,此时可以构建一个双状态NFA来描述这个状态机
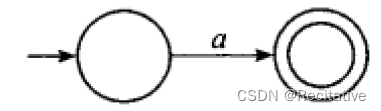
-
R = ε R = \varepsilon R=ε

-
R = ∅ R = \empty R=∅
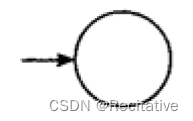
-
前三条成立,且其他类型的语言可以描述为前三种语言的正则运算,得证。
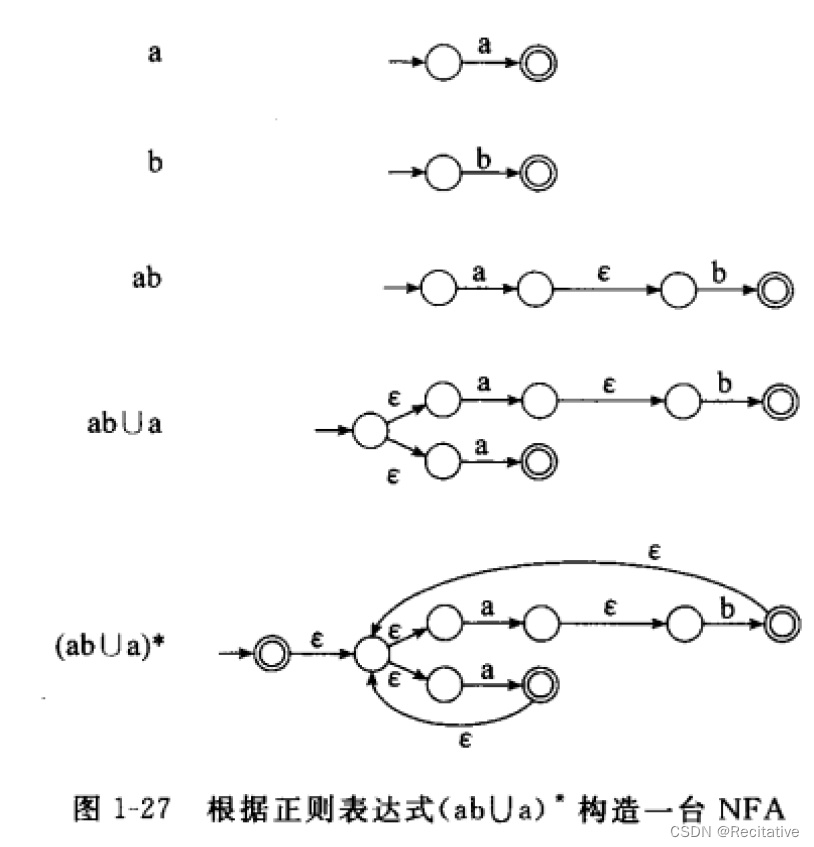
-
-
如果一个语言是正则的,则可以使用正则表达式描述该语言
-
如果语言是正则的,则一定存在一台DFA能够接受该语言(定义证)
-
DFA能够转成等价的正则表达式。
定义广义非确定型有穷自动机(GNFA)为转移箭头为正则表达式的NFA。
遵循以下步骤,将DFA转换为GNFA:
- 添加新的起始状态和新的接受状态;
- 从新的起始状态连接 ε \varepsilon ε到原来的起始状态,从原来的接受状态连接 ε \varepsilon ε到新的接受状态。
- 将多个标记的箭头改为使用 ∪ \cup ∪连接,没有连接的状态之间使用 ∅ \empty ∅连接
-
GNFA能够转换为正则表达式。
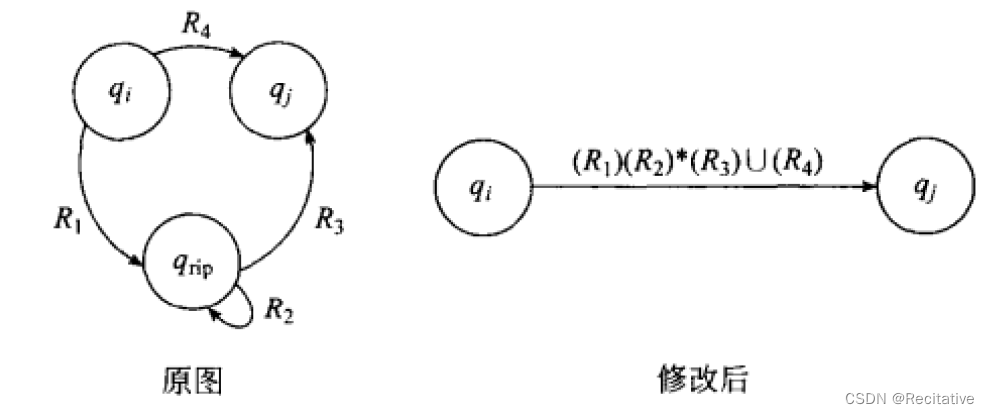
对任意状态数 > 2 >2 >2的GNFA(GNFA必须包含一个起始和一个终止),减少起始和接受之外的状态,然后修改剩下的箭头上的正则表达式,从而从 k k k状态数的GNFA,构造出 k − 1 k-1 k−1状态数的GNFA。
定义GNFA为一个5元组 ( Q , Σ , δ , q s t a r t , q a c c e p t (Q, \Sigma, \delta, q_{start}, q_{accept} (Q,Σ,δ,qstart,qaccept:
- Q为有穷状态集
- Σ \Sigma Σ为字母表
- δ : ( Q − { q a c c e p t } ) × ( Q − { q s t a r t } ) → R \delta:(Q-\{q_{accept}\})\times(Q - \{q_{start}\})\to\mathcal R δ:(Q−{qaccept})×(Q−{qstart})→R
- q s t a r t q_{start} qstart
- q a c c e p t q_{accept} qaccept
使用归纳法证明断言:对任意GNFA G G G,上述转换得到的表达式等价于 G G G
-
对 k = 2 k=2 k=2, G G G只有两个状态,可能只有一个箭头,箭头上的表达式描述了所有能够被接受的字符串,得到该表达式等价于G
-
设对 k − 1 k-1 k−1为真,则对 k k k,设剔除一个状态后的GNFA为 G ′ G' G′,对任意接受分支,G的状态序列为:
q s t a r t , q 1 , q 2 , … , q a c c e p t q_{start},q_1,q_2,\dots,q_{accept} qstart,q1,q2,…,qaccept
如果被剔除的状态 q r i p q_{rip} qrip不在序列中, G ′ G' G′一定可以接受这个运算;如果 q r i p q_{rip} qrip在分支中,设 q r i p q_{rip} qrip的位置为 q i , q r i p , q j q_i, q_{rip},q_j qi,qrip,qj,则可以得到一个新的正则表达式描述剔除该状态后的 q i , q j q_i, q_j qi,qj(相当于 k = 2 k=2 k=2)。归纳成立。
-
综上,正则语言存在一台能够接受该语言的DFA,这个DFA可以转换为一台GNFA,进而转换为正则表达式。
-
非正则证明
通常使用泵引理(pumping lemma)来证明非正则,泵引理指出所有的正则语言都有一种特殊的性质,如果能够反证某个语言不具有该性质,则可以证明该语言不是正则的。
引理:若 A A A为正则语言,则存在数 p p p,称泵长度(pumping length),使得A中任意长度不小于 p p p的字符串 s s s,都可以被分为3段, s = x y z s=xyz s=xyz,且满足:
- ∀ i ≥ 0 , x y i z ∈ A \forall i\ge0, xy^iz\in A ∀i≥0,xyiz∈A
- ∣ y ∣ > 0 |y| > 0 ∣y∣>0
- ∣ x y ∣ ≤ p |xy|\le p ∣xy∣≤p
易知,若没有条件2,定理显然成立。因为若 y y y为空串,则条件1可以任意划分,且对任意划分,都可以满足条件3。
这种找到可以重复任意次的字串的过程称为抽取。
引理证明
待证:设 M = ( Q , Σ , δ , q 1 , F ) M = (Q, \Sigma, \delta, q_1, F) M=(Q,Σ,δ,q1,F)为一台识别A的DFA, p p p为 M M M的状态数。试证泵引理成立。
第一,若 A A A中不存在长度不小于 p p p的字符串,定理显然成立。因为泵引理只对长度大于 p p p的串要求了条件。
第二,若 s ∈ A s\in A s∈A不小于 p p p,设 ∣ s ∣ = n |s| = n ∣s∣=n,则 s s s对应的状态序列长度为 n + 1 n + 1 n+1,因为 n ≥ p n \ge p n≥p,因此状态序列中一定存在重复的状态(因为状态数量大于状态类别总数,总有某个状态被访问多次)。如下图所示,设第一个重复的状态为 q i q_i qi,则可据此将串划分为 x y z xyz xyz三部分
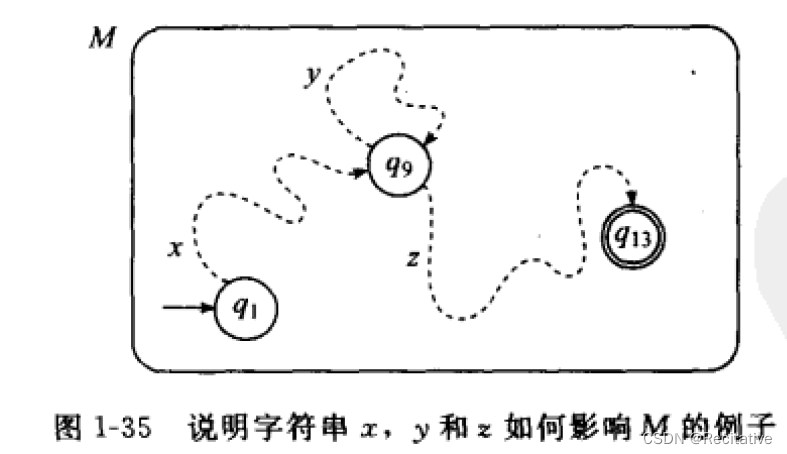
因为序列 y y y会将状态从 q i q_i qi迁移回 q i q_i qi,因此对任意 y i , i ≥ 0 y^i, i\ge 0 yi,i≥0, x y i z xy^iz xyiz都能够被接受;且 y y y显然至少为1;由于 q i q_i qi是第一个重复的状态,一定有 ∣ x y ∣ ≤ p |xy| \le p ∣xy∣≤p。
使用泵引理证明非正则
如果需要证明语言 B B B不是正则的,首先需要假设该语言正则,然后根据泵引理,找到一个不能被抽取的,长度不小于 p p p的字符串 s s s,就可以根据反证法证明。
常见的引发悖论的思路:
- 如果语言中存在不同字符、相同数量,考虑造成数量差异
- 如果语言中存在先后顺序,考虑造成逆序
例1:试证语言 { 0 n 1 n ∣ n ≥ 0 } \{0^n 1^n|n\ge0\} {0n1n∣n≥0}不是正则语言。
证明:设 B = { 0 n 1 n ∣ n ≥ 0 } B = \{0^n 1^n|n\ge0\} B={0n1n∣n≥0}正则,令 p p p为泵长度,可选 0 p 1 p 0^p 1^p 0p1p为长度一定大于 p p p的串。则 y y y串可能有三种情况:
- y y y只包含0,则 x y i z xy^iz xyiz会导致01个数不等,不成立
- y y y只包含1,同理不成立
- y y y包含0和1, x y i z xy^iz xyiz会打乱01的顺序,不成立
综上, B B B不满足泵引理,不是正则语言
简化证明:因为条件3要求 ∣ x y ∣ < p |xy| < p ∣xy∣<p,因此对串 0 p 1 p 0^p 1^p 0p1p,后两种情况会使得条件3不成立,可以简化掉。
因为已知变量只有 p p p,且有 ∣ s ∣ ≥ p |s|\ge p ∣s∣≥p的要求,一般都会围绕 p p p展开证明。
例2:试证 C = { w ∣ w 中 0 和 1 个数相同 } C=\{w|w中0和1个数相同\} C={w∣w中0和1个数相同}不是正则语言。
证明:本例是使用条件3证非正则的范例,仍然可以举前例的 0 q 1 q 0^q1^q 0q1q,由于条件3的存在, y y y只能选择包含0的情况,此时 x y i z xy^iz xyiz会使得01个数不等,因此 C C C不是正则语言。
另一种证明思路是,已知前例 B B B非正则,假设 C C C正则,则 C ∩ 0 ∗ 1 ∗ C \cap 0^*1^* C∩0∗1∗也应该正则,因为 0 ∗ 1 ∗ = 0 ∗ ∘ 1 ∗ 0^*1^*=0^* \circ 1^* 0∗1∗=0∗∘1∗,根据正则运算规律,两者求交应该正则。然而两者求交的结果为 B B B, B B B是非正则的,存在矛盾,故得 C C C非正则。
例3:试证 F = { w w ∣ w ∈ { 0 , 1 } ∗ } F = \{ww|w\in\{0,1\}^*\} F={ww∣w∈{0,1}∗}非正则。
证明: F F F为任意长度、每位可0可1的串。这种前后连接的,很大概率是要利用条件3。假设F正则,设串 s = 1 0 p 1 0 p s = 10^p10^p s=10p10p,根据条件3, x y xy xy只能在前半序列中选择,分类讨论:
- x = ε x = \varepsilon x=ε,此时 y = 1 0 ∗ y = 10^* y=10∗, x y i z = ( 1 0 ∗ ) i 0 p − ∗ 1 0 p ∉ F xy^iz = (10^*)^i0^{p-*}10^p \notin F xyiz=(10∗)i0p−∗10p∈/F,不满足条件1
- x ≠ ε x \ne \varepsilon x=ε,此时 y y y只包含0, x y i z = 1 ( 0 ∗ ) i 0 p − ∗ 1 0 p ∉ F xy^iz = 1(0^*)^i0^{p - *}10^p \notin F xyiz=1(0∗)i0p−∗10p∈/F,不满足条件1
综上, F F F非正则。
例4:试证 D = { 1 n 2 ∣ n ≥ 0 } D = \{1^{n^2}|n \ge 0\} D={1n2∣n≥0}非正则。
证明:设 D D D正则,串 s = 1 q 2 s = 1^{q^2} s=1q2,已知 n 2 = 0 , 1 , 4 , 9 , 16 , 25 , … n^2 = 0, 1, 4, 9, 16, 25, \dots n2=0,1,4,9,16,25,…;
根据条件3, ∣ x y ∣ ≤ p |xy|\le p ∣xy∣≤p,故 ∣ y ∣ ≤ p |y| \le p ∣y∣≤p,则 ∣ x y 2 z ∣ ≤ p 2 + p < p 2 + 2 p + 1 < ( p + 1 ) 2 |xy^2z| \le p^2 + p < p^2 + 2p + 1 < (p + 1)^2 ∣xy2z∣≤p2+p<p2+2p+1<(p+1)2,又因 ∣ y ∣ > 0 |y| > 0 ∣y∣>0, ∣ x y 2 z ∣ > p 2 |xy^2z| > p^2 ∣xy2z∣>p2,因此 ∣ x y 2 z ∣ ∉ n 2 |xy^2z| \notin n^2 ∣xy2z∣∈/n2, D D D非正则。
例5:试证 E = { 0 i 1 j ∣ i > j } E = \{0^i1^j|i>j\} E={0i1j∣i>j}非正则。
证明:设 E E E正则,串 s = 0 p + 1 1 p s = 0^{p + 1}1^p s=0p+11p,根据条件3, y y y只可能包含0。
设 i = 0 i = 0 i=0,则 x y i z = 0 p 1 p ∉ E xy^iz = 0^p1^p\notin E xyiz=0p1p∈/E,不满足泵引理, E E E非正则。
参考
- 《计算理论导引》第二版,机械工业出版社























 1328
1328











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










