【概率论与数理统计】1.1 随机事件及其运算

【配套教材】概率论与数理统计教程（第三版）——茆诗松

1.1.1 随机现象

• 随机现象：在一定的条件下，并不总是出现相同结果的现象称为随机现象。

例如：掷一颗骰子，结果不止一个，哪一个结果出现，人们事先也不知道。

• 确定性现象：只有一个结果的现象称为确定性现象。

例如：太阳从东方升起，水往低处流，异性电荷相吸等等。

• 随机试验：对在相同条件下可以重复的随机现象的观察、记录、试验称为随机试验。

1.1.2 样本空间

• 样本空间：随机现象的一切可能基本结果组成的集合称为样本空间，记为$\Omega$ = { $\omega$ }，其中 $\omega$ 表示基本结果，又称为样本点，样本点是今后抽样的最基本单元。

例如，抛一枚硬币的样本空间为${\Omega }_1$ = { ${\omega }_1，{\omega }_2$}，其中${\omega }_1$表示正面朝上，${\omega }_2$表示反面朝上。

注意：

（1）样本空间中的元素可以是数也可以不是数。

（2）随机现象的样本空间至少有两个样本点，如果将确定性现象放在一起考虑，则含有一个样本点的样本空间对应的为确定性现象。

（3）按样本点的个数可分为离散样本空间与连续样本空间。

1.1.3 随机事件

• 随机事件：随机现象的某些样本点组成的集合称为随机事件，简称事件，常用大写字母表示。
• 维恩（Venn）图：在概率论中常用一个长方形表示样本空间$\Omega$，用其中一个圆或者其他几何图形表示事件，这类图形称为维恩（Venn）图。

注意：

由样本空间$\Omega$中的单个元素组成的子集称为基本事件，而样本空间$\Omega$的最大子集（即$\Omega$本身）称为必然事件，样本空间$\Omega$的最小子集（即空集$\varnothing$）称为不可能事件。

1.1.4 随机变量

• 随机变量：用来表示随机现象结果的变量称为随机变量。

1.1.5 事件间的关系

• 包含关系

如果属于A的样本点必属于B，则称A被包含在B中（如图1），或称B包含A，记为A$\subset$B，或B$\supset$A。用概率论的语言说：事件A发生必然导致事件B发生。

例如，掷一颗骰子，事件A=“出现4点”，事件B=“出现偶数点”，事件A的发生必然导致事件B的发生，故A$\subset$B。

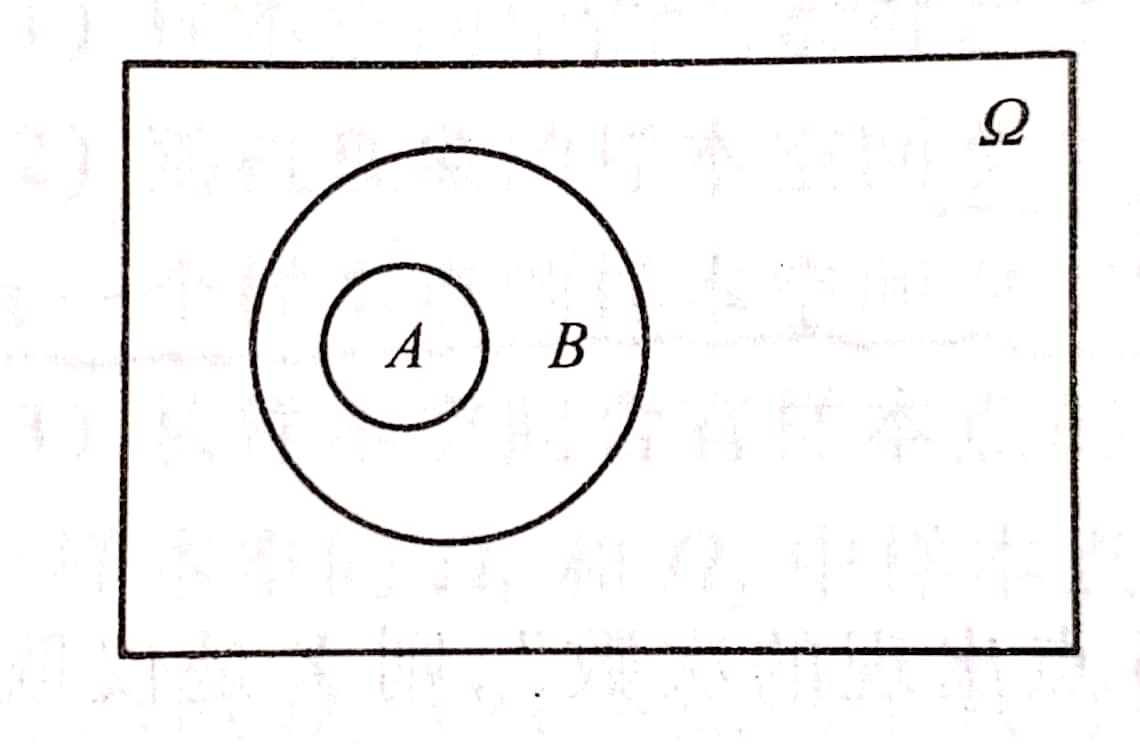
图1 包含关系

• 相等关系

如果事件A与事件B满足：属于A的样本点必属于B，而且属于B的样本点必属于A，即A$\subset$B且B$\subset$A，则称事件A与B相等，记为A=B。

例如，掷两颗骰子，以A记事件“两颗骰子的点数之和为奇数”，以B记事件“两颗骰子的点数为一奇一偶”。很容易证明：A发生必然导致B发生，而且B发生也必然导致A发生，所以A=B。

• 互不相容

如果A与B没有相同的样本点（如图2），则称A与B互不相容。用概率论的语言说：A与B互不相容就是事件A与事件B不可能同时发生。

例如，在电视机寿命试验中，“寿命小于1万小时”与“寿命大于5万小时”是两个互不相容的事件，因为它们不可能同时发生。

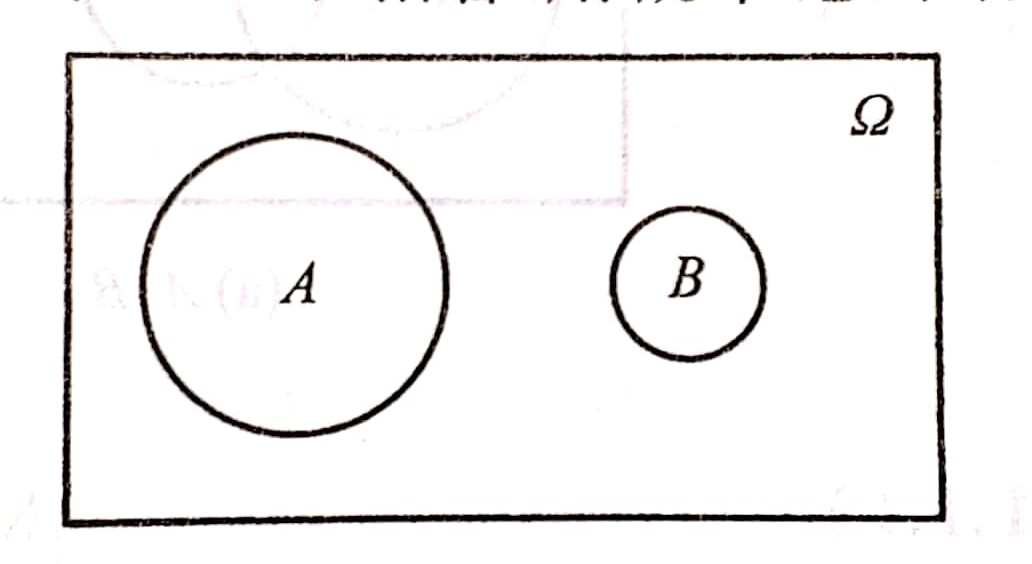
图2 互不相容

1.1.6 事件间的运算

• 事件A与B的并

记为A$\cup$B，事件A与B中至少有一个发生（如图3左）。

例如，在掷一颗骰子的试验中，记事件A=“出现奇数点”={1,3,5}，记事件B=“出现的点数不超过3”={1,2,3}，则A与B的并为A$\cup$B={1,2,3,5}。

• 事件A与B的交

记为A$\cap$B，事件A与B同时发生（如图3右）。

例如，在掷一颗骰子的试验中，记事件A=“出现奇数点”={1,3,5}，记事件B=“出现的点数不超过3”={1,2,3}，则A与B的交为A$\cap$B={1,3}。

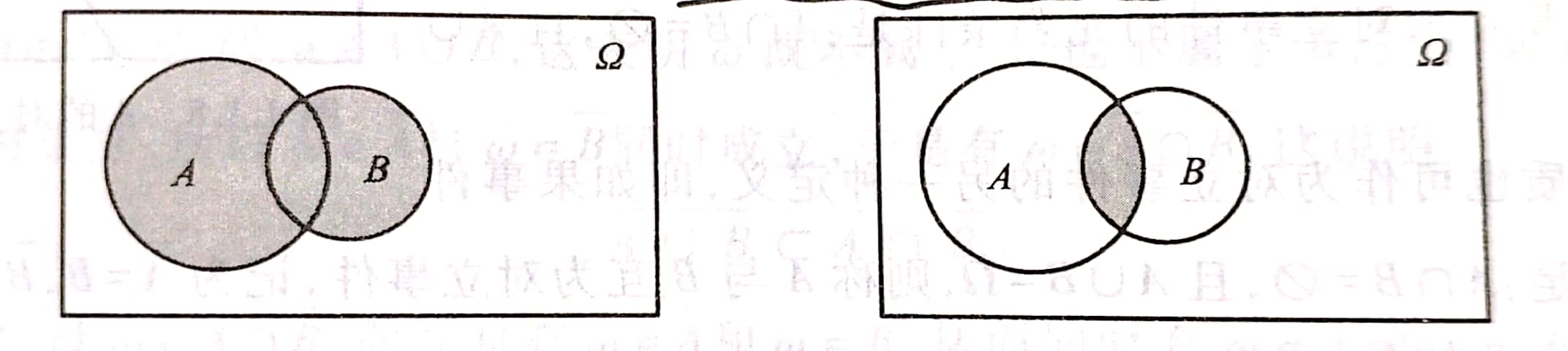
图3 并与交

• 事件A对B的差

记为A-B，事件A发生而B不发生（如图4）。

例如，在掷一颗骰子的试验中，记事件A=“出现奇数点”={1,3,5}，记事件B=“出现的点数不超过3”={1,2,3}，则A与B的交为A-B={5}。

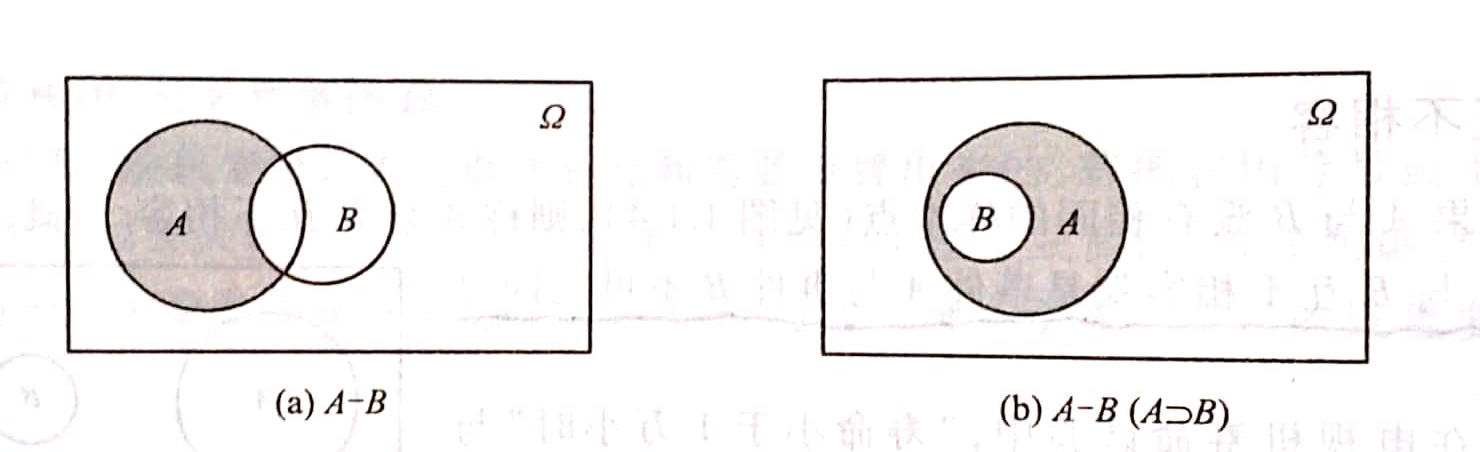
图4 差

• 对立事件

事件A的对立事件，记为$\overline{A}$，也就是A不发生，即$\overline{A}=\Omega -A$。

例如，在掷一颗骰子的试验中，事件A=“出现奇数点”={1,3,5}的对立事件是$\overline{A}$={2,4,6}。

注意：

（1）对立事件一定是互不相容的事件，即$A\cap \overline{A}=\varnothing$。但互不相容的事件不一定是对立事件。

（2）$A-B$可以记为$A\overline{B}$。

• 事件的运算性质

（1）交换律
$$A\cup B=B\cup A，AB=BA$$
（2）结合律
$$（A\cup B）\cup C=A\cup (B\cup C)$$
$$(AB)C=A(BC)$$

（3）分配律
$$(A\cup B)\cap C=AC\cup BC$$

$$(A\cap B)\cup C=(A\cup C)\cap (B\cup C)$$

（4）对偶律（德摩根公式）
$$\overline{A\cup B}=\overline{A}\cap \overline{B},\overline{A\cap B}=\overline{A}\cup \overline{B}$$

1.1.7 事件域

设$\Omega$为一样本空间，$\mathcal{F}$为$\Omega$的某些子集所组成的集合类。如果$\mathcal{F}$满足：

（1）$\Omega \in \mathcal{F}$；

（2）若$A\in \mathcal{F}$，则对立事件$\overline{A}\in \mathcal{F}$；

（3）若$A_n\in \mathcal{F}$，$n=1,2，...$，则可列并${\bigcup }_{n=1}^{\infty }{A}_n\in \mathcal{F}$

则称$\mathcal{F}$为一个事件域，又称为$\sigma$域或$\sigma$代数。

在概率论中，又称（$\Omega ，\mathcal{F}$）为可测空间。

例如，若样本空间只含有两个样本点$\Omega$={ ${\omega }_1，{\omega }_2$ }，记$A$={ ${\omega }_1$ }，$\overline{A}$={ ${\omega }_2$ }，则其事件域为$\mathcal{F}$=
{ $\varnothing ，A，\overline{A}，\Omega$ }。