KMP算法

问题引入

给定一个长度为 $n$ 的源串 $S$，长度为 $m,m\le n$ 的匹配串 $T$，求出 $T$ 在 $S$ 中第一次出现的位置（匹配子串后第一个字符的位置），若没有出现则输出 $-1$。

暴力匹配

对于源串 $S$ 的任意位置 $i(0\le i<n)$ ，枚举模式串 $T$ 的所有位置 $j(0\le j<m)$ ，如果某次检查 $m$ 个位置刚好照应，显然匹配成功。

char s[maxn], t[maxn];
int n, m;

int brouteforce() {
	for (int i = 0; i < n - m + 1; i++) {
        bool flag = 1;
        for (int j = 0; j < m; j++)
            if (s[i + j] != t[j]) {
                flag = 0;
                break;
            }
        if (flag) return i;
    }
    return -1;
}

这样做的时间复杂度显然是 $O(nm)$。

KMP算法

对于如下的例子，在 $S[5]$ 失配：

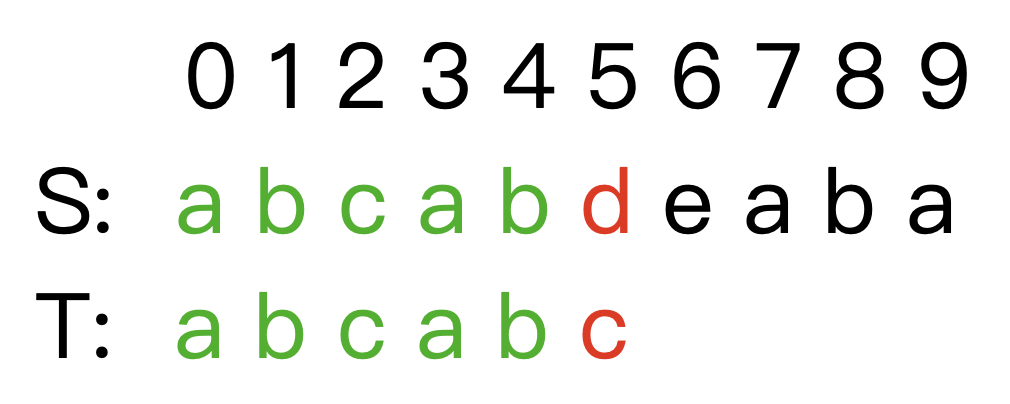
对于暴力算法，我们不难发现，如果匹配到不相同的字符，但是在最后一个不匹配的字母前已经有若干个字符匹配成功。如果只向后移动一个字符，在前面字符不重复的情况是肯定不会匹配成功，也就是说右移一次继续判断的操作是无用功。那么仔细观察已经匹配的模式串前缀部分，我们发现它可能是一个回文字符串，那么移动的时候我们就可以根据前缀回文的性质，向后移动该前缀串的最大前后缀匹配长度 $k$。

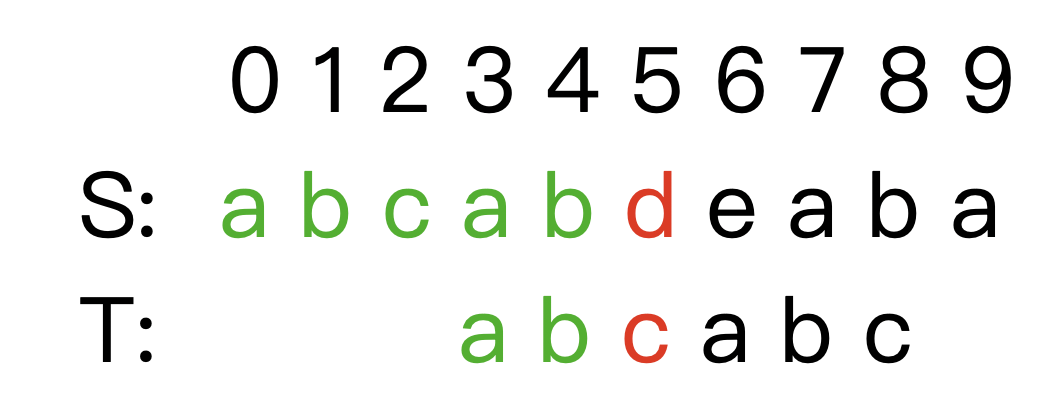
如果每次都是按照已经匹配的部分前缀来向后移动，显然时间复杂度大大降低。模式串每个前缀串 $T[0\to i]$ 的最大前后缀匹配长度为 $next[i]$。规定长度为 $i+1$ 的前缀串 $T[0\to i]$ 的 $next[i]$ 最大为 $i$，如果为 $i+1$ 代表串本身去匹配，没有意义。特别的，一个前缀若没有最大前后缀匹配，则 $next=0$。

先不考虑如何得到，假设已经得到了它，那么我们进行字符串匹配的函数如下：

设置两个指针 $i,j$ 分别指向源串和模式串，不断移动两个指针。判断两个指针位置的字符是否相等，若相等，则两个指针分别向后移动一位；若不等，则要考虑模式串的指针 $j$ 的前缀 $T[0\to j-1]$，若 $next[j-1]>0$，前缀 $T[0\to j-1]$ 存在最大前后缀匹配，这时令指针 $j=next[j-1]$，否则代表 $j$ 指向模式串的第一个字符，只需要将源串的指针向后移动。

char s[maxn], t[maxn];
int n, m, Next[maxn];

int kmp() {
    int i = 0, j = 0;
    while(i < n && j < m) {
        if(s[i] == t[j]) i++, j++;
        else {
            if(j) j = Next[j - 1];
            else i++;
        }
    }
    return j == m ? i - 1 : -1;
}

上述算法的时间复杂度为 $O(n+m)$，但是 $next$ 数组如何求？

如果考虑暴力的算法，就是对每个前缀做一次双指针扫描，这样预处理的时间复杂度为 $O(m^2)$。

$next$ 数组的核心思想是前后缀的自我匹配，考虑递推预处理，假设我们已经得到了 $next[0\to i-1]$ 了，加下来需要求 $next[i]$ ，那么分类讨论：

因为 $next[i-1]$ 已知 ，假设指针 $now=next[i-1]$ ，如果 $t[now]=t[i]$，那么显然可以在 $now$ 的基础上向后扩展一位，即 $next[i]=now+1$。

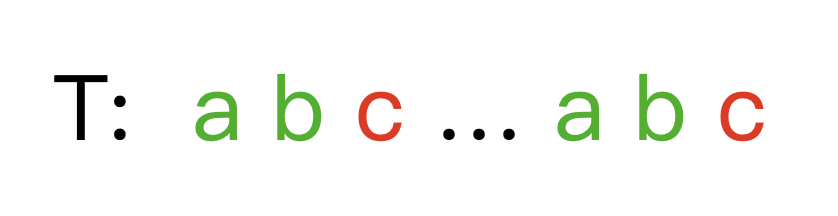
否则，如果出现了失配的情况：

这时显然需要缩短一下 $now$ 的指向，来查看是否匹配，因此在保持 “$t[0\to i-1]$ 的 k-前缀仍然等于 k-后缀”的前提下，让这个新的 $now$ 尽可能大一点。注意到现在子串 A 和子串 B 是相等的，因此使得上图左边的绿色部分的 k-前缀等于右边绿色部分的 k-后缀的最大的 $k$，其实就是子串 A 的最长公共前后缀的长度 —— $next[now-1]$ 。

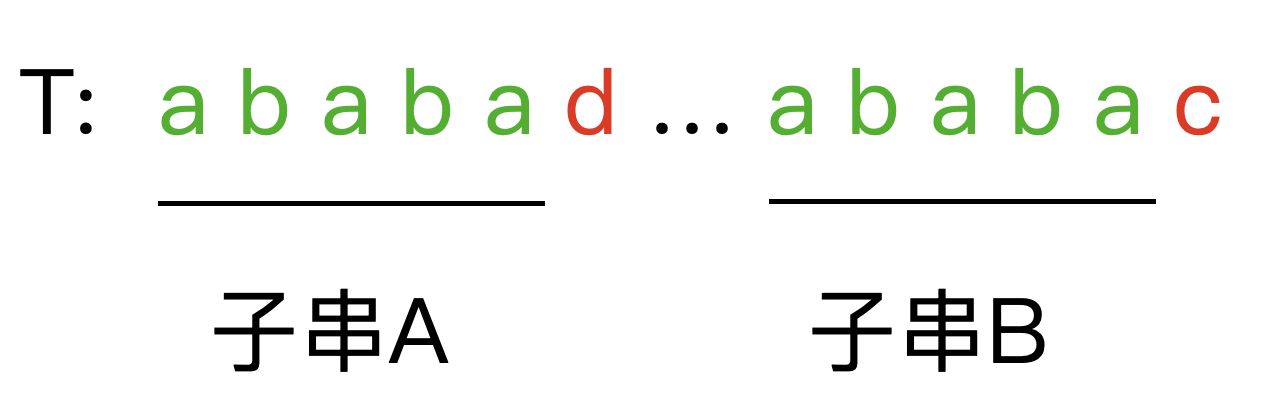
然后再考虑特殊情况，即 $now=0$ 的情况，此时显然已经没有最大前后缀匹配，那么直接令 $next[i]=0$。

int n, m;
char s[maxn], t[maxn];
int Next[maxn];


void getNext() {
    n = strlen(s), m = strlen(t);
    Next[0] = 0;
    int now = 0;
    for(int i = 1; i < m; i++) {
        while(now && t[now] != t[i]) now = Next[now - 1];
        if(t[now] == t[i]) Next[i] = ++now;
        else Next[i] = 0;
    }
}

综上，我们得到 KMP 算法如下：

int n, m;
char s[maxn], t[maxn];
int Next[maxn];


void getNext() {
    n = strlen(s), m = strlen(t);
    Next[0] = 0;
    int now = 0;
    for(int i = 1; i < m; i++) {
        while(now && t[now] != t[i]) now = Next[now - 1];
        if(t[now] == t[i]) Next[i] = ++now;
        else Next[i] = 0;
    }
}

int kmp() {
    int i = 0, j = 0;
    while(i < n && j < m) {
        if(s[i] == t[j]) i++, j++;
        else {
            if(j) j = Next[j - 1];
            else i++;
        }
    }
    return j == m ? i - 1 : -1;
}