最长上升子序列

动态规划解决最长上升子序列

问题描述：
　　给定一个任意顺序的数字序列，找出其中的最长上升子序列。给定一个数字序列$A_i$，它可以得到多个上升的子序列，不要求连续，但要求先后顺序，保证子序列后一个元素一定比前一个元素大。这些上升的子序列中的最长的一个，就是它的最长上升子序列。
　　如：给定数字序列为A={1,7,3,5,9,4,8}，它的上升子序列有{1,7}，{1,3}，{1,3,5}，{1,3,5,9}等等，最长上升子序列为{1,3,5,9}，它的最长上升子序列的长度就是4。

---

解题思路：

1. 找子问题：
   　　求以$A_k(k=0,1,2,3\dots \dots n-1)$为终点的最长上升子序列的长度。“终点”是指一个上升子序列中最右边的那个数。

【分析】：
　　这个子问题乍一看好像和原问题并不完全一样，原问题是要求整个序列的最长上升子序列，并没有指定它的终点，这个子问题却指定了它的终点。但是呢，如果以每个元素为终点的最长上升子序列都解决了，那么，整个数列的最长上升子序列不就是这ｎ个最长上升子序列中的最大值吗。

2. 确定状态：
   　　每个子问题只和一个变量的位置相关，那么，整个位置 $k$ 就是这个题的状态。每个状态对应的“值”就是以 $A_k$ 为终点的最长上升子序列的长度。

3. 递归方程：
   　　我们使用动态规划解决问题的基本思路是先确定递归方程，然后分析递归方程，再做出一些改进。这个题中我们设一个数组 MaxLen[N] 来存放以 $A_k$ 为终点的最长上升子序列的长度。
   M a x L e n [ k ] = { 1 , 初始值 m a x { M a x L e n [ k ] , M a x L e n [ j ] + 1 } , 0<=j<k MaxLen[k]=\begin{cases}1, & \text{初始值} \\max\{MaxLen[k],MaxLen[j]+1\}, & \text{0<=j<k}\end{cases} MaxLen[k]={1,max{MaxLen[k],MaxLen[j]+1},​初始值0<=j<k​　　即：
   　　（1）初始时，每个元素的最长上升子序就是它本身，长度就为1。
   　　（2）其次，元素 $A_k$ 的最长上升子序的长度就是，在 $A_k$ 左边，“终点”的数值小于 $A_k$ 且长度最大的那个上升子序列的长度加一。因为 $A_k$ 左边任何终点小于 $A_k$ 的子序列加上 $A_k$后就能形成一个更长的上升子序列。
   　　（3）如果找不到这样的一个满足条件的“终点”，那就不改变当前元素的最长子序列长度，它还是1，因为我们初始化时，每个值的最长上升子序列都初始化为1。

4. 时间复杂度：　时间复杂度 = 状态 * 每个状态的计算量。
   　　这个问题有 n 个状态，每个状态需要一个循环来计算，所以每个状态的时间复杂度是 $O(n)$，所以，这个题是时间复杂度就是 $O(n^2)$

---

写出递推代码：

#include<iostream>
using namespace std;
const int N = 100;
int max(int a, int b)
{
	int m = a > b ? a : b;
	return m;
}
int main()
{
	int n,i,j;
	cin >> n;
	int A[N];//存放原始数据
	int MaxLen[N];//存放Ak为终点的最长子序长度
	for (i = 0; i < n; i++)
	{
		cin >> A[i];
		MaxLen[i] = 1;//初始化为1

	}
	for (i = 1; i < n; i++)//求以Ai为终点的最长上升子序列的长度
	{
		for (j = 0; j < i; j++)//查看Ak左边的的元素的最长上升子序列。
		{
			if (A[i]>A[j])
			{
				MaxLen[i] = max(MaxLen[i], MaxLen[j] + 1);//每次更新
			}
		}
		
	}
	int max = MaxLen[0];
	for (i = 0; i < n; i++)
	{
		if (MaxLen[i] > max)
			max = MaxLen[i];
	}
	cout << max << endl;
	return 0;
}

可能有人会问，MaxLen[i] = max(MaxLen[i], MaxLen[j] + 1);这一句为什么不直接把MaxLen[j] + 1)赋值给MaxLen[i]呢？为什么还要进行一次比较？
　　因为MaxLen[i]的值在前面可能经过更新，它比MaxLen[j] + 1)还要大，所以，需要一次比较。
将上面那个数列 A={1,7,3,5,9,4,8} 做一点改变，将 4 改为 2 ，B={1,7,3,5,9,2,8}。

初始：

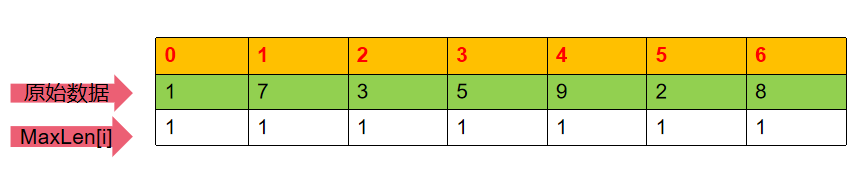
经过几次循环，计算出前6个元素以每个元素为终点的最长子序列如下表：

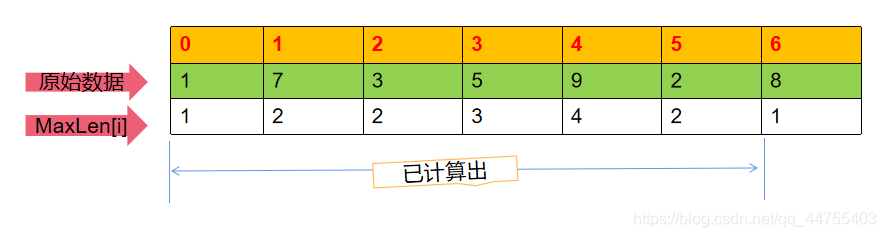
现要计算以最后一个元素为“终点”在最长上升子序列，由前面五个元素（1,7,3,5,9）进行递推，得出8的“暂时”上升子序列长度为4，再和元素2进行比较，满足if (A[i]>A[j])的关系，如果这时直接将MaxLen[j] + 1赋值给MaxLen[i]，那么，元素8的最长上升子序列就变成了3，而不是正确的4。所以，就会发生错误。

所以，需要进行MaxLen[i] = max(MaxLen[i], MaxLen[j] + 1);，取较大值。

---

其他的动态规划问题：

浅谈动态规划
动态规划解决数字三角形问题
动态规划解决最长公共子序列

学海无涯