局部最优解的误区与真相

本文原文来自微信平台我的个人公众号：算法仓库，直接复制的，里面有些数学公式，可能没有完全黏贴，原文链接：如下：局部最优解的误区与真相

1. 概念

局部最优解和全局最优解是我们在优化中经常提到的概念，今天让我们来探讨一下优化算法中局部最优解与全局最优解的概念。首先，我们需要明确这两个术语的定义。

在优化问题中，全局最优解是指在所有可能的解中，目标函数值最佳的解。换句话说，它是整个解空间中的最高点（或最低点，具体取决于问题的设定）。

而局部最优解则是在解空间的某个局部区域内，目标函数值最佳的解。因此，局部最优解虽然在其邻近区域是最优的，但并不一定是全局最优解。

2. 举例说明

2.1 宏观说明

为了更直观地理解这一概念，我们可以想象一个山地景观。假设你站在一个山峰上，环顾四周，你所处的位置比周围的任何地方都要高。然而，这并不意味着你已经达到了世界之巅。或许在更远的地方，存在一个更高的山峰。在这个比喻中，你所站的山峰就是一个局部最优解，而那个更高的山峰则是全局最优解。

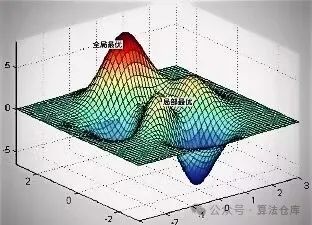
这张图片是一个三维函数的图形，用于展示局部最优解和全局最优解的概念。图中的曲面代表了某个函数的值，随着x和y两个变量的变化而变化。

（1）全局最优：图中用红色标注的点是全局最优解。这个点位于曲面的最高点，表示在整个定义域内，这个点的函数值是最大的。

（2）局部最优：图中用黄色标注的点是局部最优解。这个点位于曲面的一个较高点，但不是最高点。在这一点的周围，函数值都比它低，所以它是局部最优的。然而，当我们考虑整个定义域时，全局最优解（红色点）的函数值更大。

为了更好地从直观说明优化算法中的搜索过程和局部最优解的概念。我们看下图。这个图形直观地展示了优化算法在复杂函数表面上寻找最优解的过程图中的搜索路径显示了算法如何在函数表面上移动，尝试找到最优解。

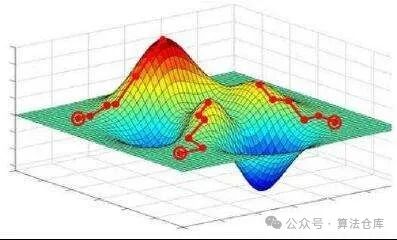
让我带着读者分析一下上图中的元素，首先

（1）三维曲面：图中的曲面代表了某个函数的值，随着x和y两个变量的变化而变化。颜色通常用来表示函数值的大小，例如，红色可能较高的函数值，而蓝色可能代表较低的函数值。

（2）全局最优解：图中最高的红色点代表全局最优解，即在整个定义域内函数值最大的点。

（3）局部最优解：图中除了全局最优解之外，还有其他一些较高的点，这些可能是局部最优解。局部最优解在其邻域内是最优的，但在整个定义域内不是最优的。

（4）搜索路径：图中用红线连接的一系列红色圆圈可能代表了优化算法的搜索路径。这些点显示了算法在寻找最优解过程中的迭代步骤。

（5）鞍点：在全局最优解和局部最优解之间的低点可能是鞍点。鞍点是函数在某些方向上是局部最大值，在其他方向上是局部最小值的点。

2.2 实例说明

接下来，我们可以通过一个具体的例子来进一步说明这一点。假设我们有一个函数。为了找到它的最小值，我们可以对函数求导并令导数为零。具体步骤如下：

令，解得：

将 代入原函数，得到：

因此， 是函数 的一个临界点。为了确定它是最小值点，我们可以进一步检查二阶导数：

由于，说明 是一个局部最小值点。在这个例子中，由于函数 是一个开口向上的抛物线，我们会想到这个局部最小值点同时也是全局最小值点。

且慢，这真的是全局最小值吗？让我们细细思量。函数可以重写为。由于平方总是非负的，因此当时，函数取得最小值0。由此可见，在这种情况下，局部最小值实际上也是全局最小值。

然而，若函数有多个局部最小值和最大值，情况又将如何呢？以为例，我来带着读者朋友来详细一步一步探讨一番。

首先，求导数：

令导数等于零：

利用二次公式求解：

因此，临界点为 和。接下来，我们通过二阶导数来判断这些点的性质：

在第一个临界点处求值：

因此，这是一个局部最小值点。

在第二个临界点处：

因此，此处为局部最大值。

若将此函数绘制成图，可见函数在 处达到局部最大值，随后下降至 处的局部最小值，再逐渐上升。然而，全局最小值又在何处？随着 趋向于正无穷或负无穷，函数值亦随之趋向于正无穷，故此函数无全局最小值——它在局部最小值处下降，但无下界。

如此，我们已理解了局部最优解与全局最优解的概念。

因此，总结而言，全局最优解是整个解空间中最佳的解，而局部最优解则是其邻域内最佳的解，但未必是全局最优解。优化算法可能陷入局部最优解，特别是当存在多个局部最优解时，找到全局最优解颇具挑战!

注：图中两个图片来源于图片百度