求相关树变形题目持续更新

下面的题目不要构造辅助函数求解：

单值二叉树

1.题目描述

2.题目链接

力扣

3.解题思路

class Solution {
public:
    bool isUnivalTree(TreeNode* root) 
    {
        if(root==NULL)
        {
            return true;
        }
        if(root->left&&root->val!=root->left->val)
        {
            return false;
        }
        if(root->right&&root->val!=root->right->val)
        {
            return false;
        }

        return isUnivalTree(root->left)&&isUnivalTree(root->right);
    }
};

相同的树

1.题目描述

2.题目链接

力扣

3.解题思路

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) 
    {
        if(p==NULL&&q==NULL)
        {
            return true;
        }
        if(q==NULL||p==NULL)
        {
            return false;
        }

        if(p->val!=q->val)
        {
            return false;
        }

        return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
    }
};

求二叉树的最大深度

1.题目描述

2.题目链接

牛客
力扣

3.解题思路

int maxDepth(struct TreeNode* root)
{
    if(root==NULL)
    {
        return 0;
    }
    int RightDepth=maxDepth(root->right);
    int LeftDepth=maxDepth(root->left);
    return RightDepth>LeftDepth?RightDepth+1:LeftDepth+1;
}

翻转二叉树

1.题目描述

2.题目链接

力扣

3.解题方法

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) 
    {
        if(root==NULL)
        {
            return root;
        }

        TreeNode* left=invertTree(root->left);
        TreeNode* right=invertTree(root->right);
        root->right=left;
        root->left=right;
        return root;
    }
};

二叉树的镜像

1.题目描述

2.题目链接

力扣
牛客

3.解题方法

class Solution {
public:
    TreeNode* mirrorTree(TreeNode* root) 
    {
        if(root==NULL)
        {
            return root;
        }
        
        TreeNode* left=mirrorTree(root->left);
        TreeNode* right=mirrorTree(root->right);

        root->right=left;
        root->left=right;
        return root;
    }
};

另一颗树的子树(这题不是剑指offer，是普通题目和剑指offer不一样测试用例）

1.题目描述

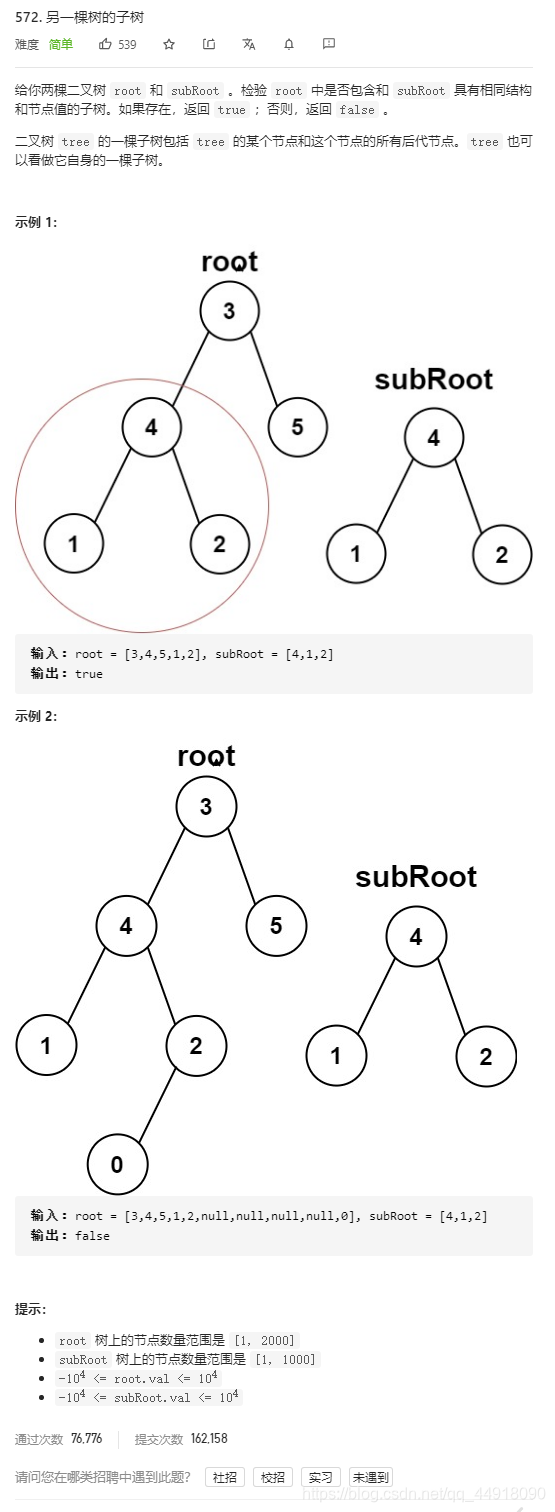
2.题目链接

力扣

3.解题思路

class Solution {
public:
    bool IsSameTree(TreeNode* p,TreeNode* q)
    {
        if(p==NULL&&q==NULL)
        {
            return true;
        }
        if(p==NULL||q==NULL)
        {
            return false;
        }
        if(p->val!=q->val)
        {
            return false;
        }
        return IsSameTree(p->left,q->left)&&IsSameTree(p->right,q->right);
    }
    bool isSubtree(TreeNode* root, TreeNode* subRoot) 
    {
        if(root==NULL||subRoot==NULL)
        {
            return false;
        }
        if(IsSameTree(root,subRoot))
        {
            return true;
        }
        return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
    }
};

合并二叉树

1.题目描述

2.题目链接

力扣

3.解题思路

class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) 
    {
        if(root1==NULL)
        {
            return root2;
        }
        if(root2==NULL)
        {
            return root1;
        }
        if(root1&&root2)
        {
            root1->val=root1->val+root2->val;
        }

        root1->left=mergeTrees(root1->left,root2->left);
        root1->right=mergeTrees(root1->right,root2->right);
        return root1;
    }
};

下面的题目要构造辅助函数求解：

对称二叉树

1.题目描述

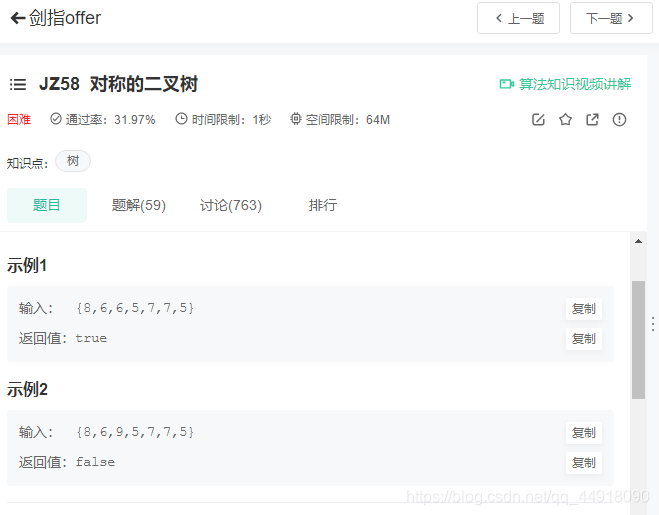
2.题目链接

力扣
牛客

3.解题思路

class Solution {
public:
    bool isMirror(TreeNode* p,TreeNode* q)
    {
        if(p==NULL&&q==NULL)
        {
            return true;
        }
        if(p==NULL||q==NULL)
        {
            return false;
        }

        if(p->val!=q->val)
        {
            return false;
        }
        
        return isMirror(p->left, q->right)&&isMirror(p->right, q->left);
    }
    bool isSymmetrical(TreeNode* pRoot) 
    {
        if(pRoot==NULL)
        {
            return true;
        }
        return isMirror(pRoot->left,pRoot->right);
    }

};

求树的子结构

1.题目描述

2.题目链接

牛客
力扣

3.解题思路

注释

class Solution {
public:
bool hasSubStructure(TreeNode*A, TreeNode*B)
{
    if(B==NULL)       //递归结束条件1：A的一个节点B的对应位置没有,可以认为是子结构
        return true;
    if(A==NULL)
    {
        return false;
    }

    //递归结束条件2：B的一个节点A的对应位置没有 / A,B对应位置节点值不同，此时必然不可能是子结构
    if ( A->val != B->val)  
    {
        return false;       
    }        

    return hasSubStructure(A->left, B->left) && hasSubStructure(A->right, B->right); 
    //返回值：继续在对应位置递归判断
}


bool isSubStructure(TreeNode *A, TreeNode *B)
{
    if(A==NULL||B==NULL)
    {
        return false;
    }
    // 根节点相同的话直接进入比较，根节点不相同看B是不是A的左/右子树的子结构
    if( hasSubStructure(A, B))
    {
        return true;
    }
    return  isSubStructure(A->left, B) || isSubStructure(A->right, B);
}

};

---

class Solution {
public:
    bool IsSameTree(TreeNode* p,TreeNode* q)
    {
        if(q==NULL)
        {
            return true;
        }
        if(p==NULL)
        {
            return false;
        }
        if(p->val!=q->val)
        {
            return false;
        }
        return IsSameTree(p->left,q->left)&&IsSameTree(p->right,q->right);
    }
    bool isSubStructure(TreeNode* A, TreeNode* B) 
    {
        if(A==NULL||B==NULL)
        {
            return false;
        }
        if(IsSameTree(A,B))
        {
            return true;
        }
        return isSubStructure(A->left,B)||isSubStructure(A->right,B);
    }
};

平衡二叉树

1.题目描述

2.题目链接

牛客
力扣

3.解题方法

判空以及递归跳出条件
int leftDepth = Depth(root->left); // 获取左子树深度
int rightDepth = Depth(root->right); // 获取右子树深度
满足三个条件才是平衡二叉树

1. 左子树和右子树深度差不超过1
2. 递归判断左子树为平衡二叉树
3. 递归判断右子树为平衡二叉树

class Solution {
public:
    int maxDepth(TreeNode* root)
    {
        if(root==NULL)
        {
            return 0;
        }

        int leftDepth=maxDepth(root->left);
        int rightDepth=maxDepth(root->right);

        return leftDepth>rightDepth?leftDepth+1:rightDepth+1;
    }
    bool isBalanced(TreeNode* root) 
    {
        if(root==NULL)
        {
            return NULL;
        }

        int leftDepth=maxDepth(root->left);
        int rightDepth=maxDepth(root->right);

        return abs(leftDepth-rightDepth)<2&&isBalanced(root->left)&&isBalanced(root->right);
    }
};