近红外数据处理-2

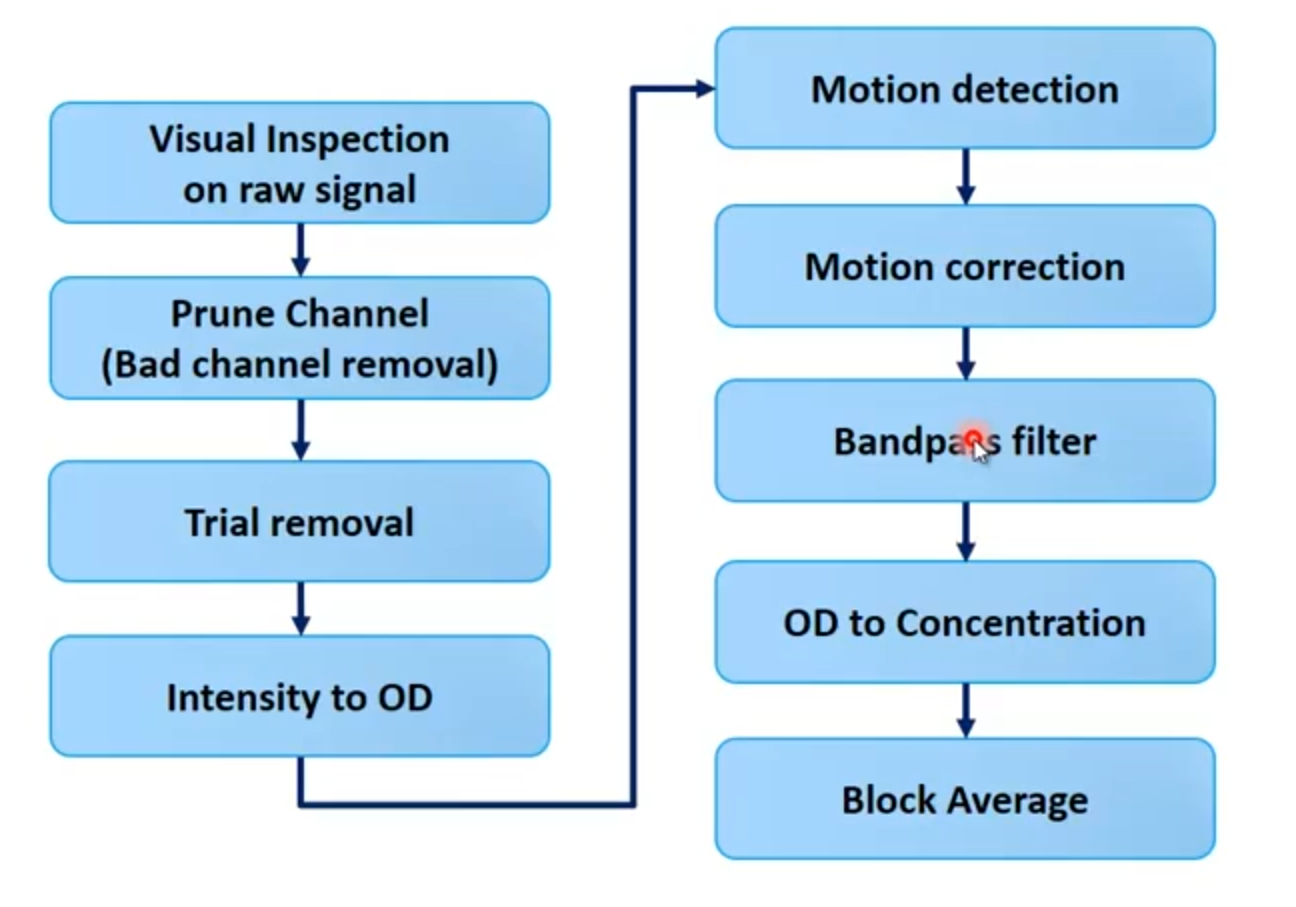
卢家峰处理的工作流

0.01-0.1或者0.2Hz的这个频率区间范围内。
0.2-2.5HZ的有心跳呼吸等非脑功能血氧相关的特征。

查看信号

因为头部的动作会带来血氧信号的改变，所以我们对于近红外数据可以进行相关的剔除。但是我使用的数据，Aux(加速度计感应信号并不存在)。

在Homer2中的View中查看plot power spectrum

Homer2和Homer3存在差异。

我们可以看到这些信号的主要分析频率集中在2.5Hz以下。
真正有效的信号是0.01Hz到0.1Hz之间。
心跳周期在0.83Hz左右，会有心跳。
因为运动任务心跳会加速，可能在1.1Hz左右。

好像确实找不到心跳的peak。

血管壁的是0.1HZ左右。

近程红外处理器的剔除

数据的筛查

刺激的设置

新版本的homer3设置为了tsv文件编辑器

对于同样事件的处理，我们可以删除剩余的时间标记，使用次数和实验时长来切割。

如果有这个选项，可以通过这个信号来进行运动起始的更准确的判断。

分析流

推荐的处理流程

对于channel的判断和移除

裁剪后，做插值，
使用小波和
（需要先计算出两个值之后再使用）CBSI都比较好用。CBSI 的核心思想是利用氧合血红蛋白（HbO）和脱氧血红蛋白（HbR）信号之间的负相关关系来校正信号。

多次运动矫正，处理的效果最好。
并非是最优的，但是可以覆盖很多场景。

如果stmi处理好的话，可以直接来一个hmrR_BlockAvg。

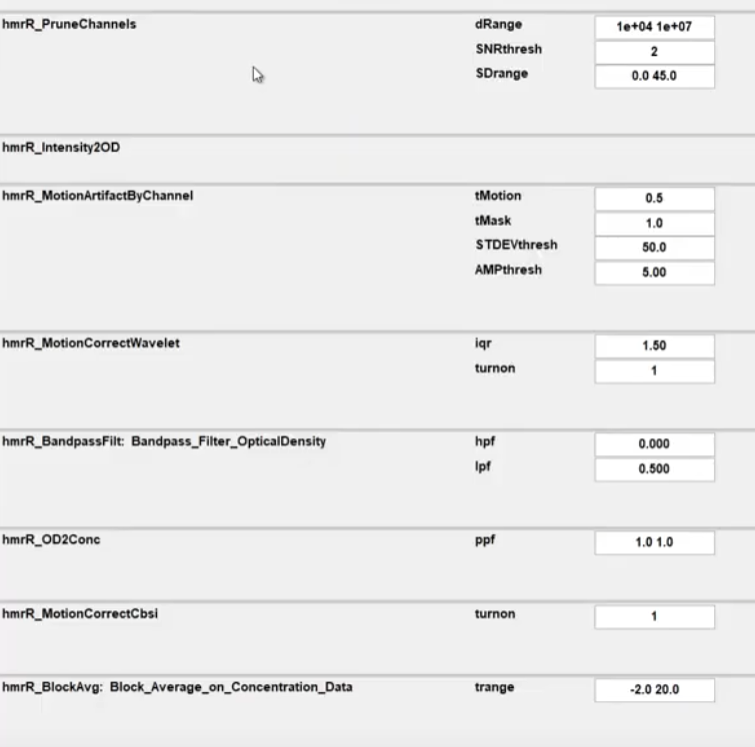
参数的选择，因为如果是光的强度信息（其强度一般在几千到几万）但具体范围取决于设备、光源功率、探测器灵敏度以及实验设置。

所以视频中的大概率是光密度的raw data

这是推荐的参数，但是仍然需要根据实际的数据进行调整。
因为涉及到的传感器的单位，测得的值的域比较奇怪，所以不进行通道的滤除。

处理之后的HbO和HbR单位不太对。

其变化趋势是正确的。但是数值不太对应的上。
通过一些

在研究 fNIRS 数据的变化性时，可以使用多种指标来量化信号的变化特征。这些指标可以帮助你更好地理解大脑活动的动态特性。以下是常用的变化性指标及其计算方法：
通常使用变异系数来判断有效性。

---

1. 标准差（Standard Deviation, SD）

• 定义：标准差是衡量数据离散程度的指标，反映了信号围绕均值的波动情况。
• 适用场景：用于评估信号的整体波动性。
• 公式：
  $$SD=\sqrt{\frac{1}{N-1}\sum _{i=1}^N(x_i-\bar{x}{)}^2}$$
  其中：
  • ( x_i ) 是第 ( i ) 个时间点的信号值。
  • ( \bar{x} ) 是信号的均值。
  • ( N ) 是时间点的总数。

---

2. 变异系数（Coefficient of Variation, CV）

• 定义：变异系数是标准差与均值的比值，用于比较不同信号之间的相对变化性。
• 适用场景：适用于比较不同通道或不同受试者之间的变化性。
• 公式：
  $$CV=\frac{SD}{\bar{x}}$$

---

3. 均方根（Root Mean Square, RMS）

• 定义：均方根是信号幅度的平均值，反映了信号的整体强度。
• 适用场景：用于评估信号的整体能量。
• 公式：
  $$RMS=\sqrt{\frac{1}{N}\sum _{i=1}^N{x}_i^2}$$

---

4. 信号幅度面积（Signal Amplitude Area, SAA）

• 定义：信号幅度面积是信号绝对值的时间积分，反映了信号的总变化量。
• 适用场景：用于评估信号的总变化量。
• 公式：
  $$SAA=\sum _{i=1}^N|x_i|$$

---

5. 动态范围（Dynamic Range）

• 定义：动态范围是信号最大值与最小值的差值，反映了信号的波动范围。
• 适用场景：用于评估信号的极端变化。
• 公式：
  $$DynamicRange=\max (x_i)-\min (x_i)$$

---

6. 近似熵（Approximate Entropy, ApEn）

• 定义：近似熵是衡量信号复杂性的指标，反映了信号的随机性和不可预测性。
• 适用场景：用于评估信号的复杂性。
• 计算方法：
  • 需要设置参数 ( m )（嵌入维度）和 ( r )（容差）。
  • 具体计算方法较为复杂，可以参考相关文献或使用工具箱（如 MATLAB 的 approximateEntropy 函数）。

---

7. 样本熵（Sample Entropy, SampEn）

• 定义：样本熵是近似熵的改进版本，用于衡量信号的复杂性。
• 适用场景：用于评估信号的复杂性，适用于短时间序列。
• 计算方法：
  • 类似于近似熵，但更稳定。

---

8. 功率谱密度（Power Spectral Density, PSD）

• 定义：功率谱密度是信号在频域上的能量分布，反映了信号的频率特性。
• 适用场景：用于分析信号的频率成分。
• 计算方法：
  • 使用傅里叶变换计算信号的功率谱。
  • 可以提取特定频带（如 0.01-0.1 Hz）的能量作为变化性指标。

---

9. 滑动窗口分析（Sliding Window Analysis）

• 定义：在时间序列上滑动一个固定大小的窗口，计算每个窗口内的变化性指标（如标准差、RMS 等）。
• 适用场景：用于分析信号的变化性随时间的变化。

---

10. 分形维数（Fractal Dimension, FD）

• 定义：分形维数是衡量信号自相似性的指标，反映了信号的复杂性和不规则性。
• 适用场景：用于评估信号的复杂性。
• 计算方法：
  • 常用的方法包括 Higuchi 分形维数和盒计数法。

---

11. Hurst 指数（Hurst Exponent）

• 定义：Hurst 指数是衡量时间序列长期依赖性的指标，反映了信号的自相似性。
• 适用场景：用于评估信号的长程相关性。
• 计算方法：
  • 使用重标极差分析（R/S 分析）或小波变换。

---

12. 相位同步（Phase Synchronization）

• 定义：相位同步是衡量两个信号之间相位关系的指标，反映了信号之间的协同性。
• 适用场景：用于分析不同通道或区域之间的功能连接。

---

代码示例

以下是一个 MATLAB 代码示例，计算 HbO 信号的标准差和变异系数：

% 假设 HbO 是一个时间序列（nTimePoints × 1）
HbO = data.procResult.conc_HbO(:, 1); % 取第一个通道的 HbO 数据

% 计算标准差
SD = std(HbO);
fprintf('Standard Deviation: %.4f\n', SD);

% 计算变异系数
CV = std(HbO) / mean(HbO);
fprintf('Coefficient of Variation: %.4f\n', CV);

---

相关文献

以下是一些关于 fNIRS 变化性指标的文献：

1. 标准差和变异系数：

   • Scholkmann, F., Kleiser, S., Metz, A. J., Zimmermann, R., Mata Pavia, J., Wolf, U., & Wolf, M. (2014). A review on continuous wave functional near-infrared spectroscopy and imaging instrumentation and methodology. NeuroImage, 85, 6-27.

2. 近似熵和样本熵：

   • Richman, J. S., & Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology, 278(6), H2039-H2049.

3. 分形维数和 Hurst 指数：

   • Higuchi, T. (1988). Approach to an irregular time series on the basis of the fractal theory. Physica D: Nonlinear Phenomena, 31(2), 277-283.

4. 功率谱密度：

   • Welch, P. D. (1967). The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Transactions on Audio and Electroacoustics, 15(2), 70-73.

---

总结

• 变化性指标可以帮助你量化 fNIRS 信号的动态特性。
• 常用的指标包括标准差、变异系数、均方根、近似熵、功率谱密度等。
• 根据研究目标选择合适的指标，并结合具体实验设计进行分析。

如果你有更多问题或需要进一步的帮助，请随时告诉我！

ai生成的

使用ai，构建一个数据处理的流程说明：
未测试。

回顾任务目标和数据处理流程来明确需要提取的数据。以下是详细的梳理：

---

1. 任务回顾

• 任务目标: 评估帕金森病人的运动能力，使用近红外脑功能数据（fNIRS）。
• 运动范式: 手指对捏、拿方块、握拳维持。
• 数据类型: 近红外脑功能数据（fNIRS），主要关注氧合血红蛋白（Oxy-Hb）、脱氧血红蛋白（Deoxy-Hb）和总血红蛋白（Total-Hb）的变化。
• 回归目标: 可能是运动能力评分、任务完成时间或准确率等连续变量。

---

2. 需要提取的数据

根据任务目标，您需要提取以下数据：

(1) 血红蛋白浓度数据

• 氧合血红蛋白（Oxy-Hb）: 反映大脑皮层的神经活动。
• 脱氧血红蛋白（Deoxy-Hb）: 反映局部氧耗。
• 总血红蛋白（Total-Hb）: 反映局部血流量变化。

(2) 试次数据

• 每个试次（手指对捏、拿方块、握拳维持）的血红蛋白浓度变化。
• 试次的基线数据（任务前的静息状态）。
• 试次的任务数据（任务执行期间）。

(3) 时间序列特征

• 均值: 试次期间血红蛋白浓度的平均值。
• 标准差: 试次期间血红蛋白浓度的波动情况。
• 峰值: 试次期间血红蛋白浓度的最大值。
• 斜率: 血红蛋白浓度随时间的变化趋势。

(4) 频域特征

• 功率谱密度: 反映血红蛋白浓度变化的频率特性。

(5) 运动分型相关数据

• 根据运动分型量表（震颤/中轴症状得分），提取不同分型病人的血红蛋白浓度特征。

---

3. 数据提取流程

以下是具体的数据提取步骤：

(1) 提取血红蛋白浓度数据

• 使用 hmrOD2Conc 将光密度（OD）数据转换为血红蛋白浓度数据。
• 提取 Oxy-Hb、Deoxy-Hb 和 Total-Hb 的时间序列。

(2) 提取试次数据

• 根据任务时间标记，截取每个试次的数据。
• 提取基线时间段（如任务前 5 秒）和任务时间段（如任务执行期间 10 秒）。

(3) 计算时间序列特征

• 对每个试次，计算 Oxy-Hb、Deoxy-Hb 和 Total-Hb 的均值、标准差、峰值和斜率。

(4) 计算频域特征

• 对每个试次，使用傅里叶变换或小波变换计算功率谱密度。

(5) 结合运动分型

• 根据运动分型量表，将病人分为步态障碍为主、震颤为主、强直-迟缓型。
• 提取不同分型病人的血红蛋白浓度特征。

---

4. 代码示例

以下是一个简单的 MATLAB 代码示例，展示如何提取试次数据和计算特征：

% 假设 conc 是血红蛋白浓度数据，shape 为 (时间点, 通道数, 血红蛋白类型)
% trials 是试次时间标记，shape 为 (试次数, 2)，每行包含试次的开始和结束时间

% 提取试次数据
baseline_window = 5 * fs; % 基线时间段（5秒）
task_window = 10 * fs; % 任务时间段（10秒）

for i = 1:size(trials, 1)
    start_time = trials(i, 1);
    end_time = trials(i, 2);
    
    % 提取基线数据
    baseline_data = conc(start_time - baseline_window : start_time, :, :);
    
    % 提取任务数据
    task_data = conc(start_time : end_time, :, :);
    
    % 计算均值
    baseline_mean = mean(baseline_data, 1);
    task_mean = mean(task_data, 1);
    
    % 计算标准差
    baseline_std = std(baseline_data, 0, 1);
    task_std = std(task_data, 0, 1);
    
    % 计算峰值
    baseline_peak = max(baseline_data, [], 1);
    task_peak = max(task_data, [], 1);
    
    % 计算斜率
    baseline_slope = polyfit(1:size(baseline_data, 1), baseline_data, 1);
    task_slope = polyfit(1:size(task_data, 1), task_data, 1);
    
    % 保存结果
    trial_features(i).baseline_mean = baseline_mean;
    trial_features(i).task_mean = task_mean;
    trial_features(i).baseline_std = baseline_std;
    trial_features(i).task_std = task_std;
    trial_features(i).baseline_peak = baseline_peak;
    trial_features(i).task_peak = task_peak;
    trial_features(i).baseline_slope = baseline_slope;
    trial_features(i).task_slope = task_slope;
end

---

5. 总结

您需要提取的数据包括：

1. 血红蛋白浓度数据（Oxy-Hb、Deoxy-Hb、Total-Hb）。
2. 试次数据（基线数据和任务数据）。
3. 时间序列特征（均值、标准差、峰值、斜率）。
4. 频域特征（功率谱密度）。
5. 运动分型相关特征。

通过以上步骤，您可以系统地提取所需数据，并为后续的回归分析提供高质量的特征输入。如果有进一步的问题，欢迎随时提问！
针对您的任务（帕金森病人的运动能力评估，使用近红外脑功能数据），以下是推荐的预处理流程及对应的 Homer2 函数：

---

1. 数据导入与初步整理

• 函数: hmrFlowInput
• 作用: 导入原始数据并进行初步整理，确保数据格式正确。

---

2. 光强度数据转换为光密度（OD）

• 函数: hmrIntensity2OD
• 作用: 将原始光强度数据转换为光密度（OD）数据，这是后续分析的基础。

---

3. 去除全局噪声与漂移

• 函数: hmrBandpassFilt
• 作用: 使用带通滤波器（如 0.01-0.5 Hz）去除低频漂移和高频噪声（如心跳、呼吸）。
• 参数建议:
  • 低频截止频率：0.01 Hz（去除漂移）。
  • 高频截止频率：0.5 Hz（去除心跳等高频噪声）。

---

4. 运动伪影检测与校正

• 函数: hmrMotionArtifact + hmrMotionCorrectWavelet（或 hmrMotionCorrectPCA）
• 作用:
  • 先使用 hmrMotionArtifact 检测运动伪影。
  • 然后使用 hmrMotionCorrectWavelet（小波变换）或 hmrMotionCorrectPCA（PCA方法）校正运动伪影。
• 选择依据:
  • 如果数据中运动伪影较多且复杂，推荐使用 hmrMotionCorrectWavelet。
  • 如果数据中运动伪影较少且简单，推荐使用 hmrMotionCorrectPCA。

---

5. 剔除无效通道

• 函数: enPruneChannels
• 作用: 剔除信号质量较差或无效的通道，确保后续分析的可靠性。

---

6. 光密度数据转换为血红蛋白浓度

• 函数: hmrOD2Conc
• 作用: 将光密度（OD）数据转换为氧合血红蛋白（Oxy-Hb）、脱氧血红蛋白（Deoxy-Hb）和总血红蛋白（Total-Hb）浓度数据。

---

7. 剔除刺激相关伪影

• 函数: enStimRejection
• 作用: 剔除与任务刺激相关的伪影或噪声，确保数据纯净。

---

8. 数据标准化

• 函数: 自定义标准化（如 z-score 标准化）
• 作用: 对每个通道的数据进行标准化，消除通道间的基线差异。
• 实现方式:
  • 使用 MATLAB 或 Python 的标准化函数（如 zscore）。

---

9. 试次截取与基线校正

• 函数: 自定义脚本
• 作用:
  • 根据任务时间标记截取每个试次的数据。
  • 使用试次前的基线时间段（如任务前 5 秒）进行基线校正。
• 实现方式:
  • 使用 Homer2 的 hmrBlockAvg 或自定义脚本。

---

10. 数据可视化与检查

• 函数: plotTrials
• 作用: 绘制试次数据，检查预处理效果。

---

完整预处理流程示例

% 1. 导入数据
rawData = hmrFlowInput('your_data_file.nirs');

% 2. 光强度转光密度
dod = hmrIntensity2OD(rawData);

% 3. 带通滤波
dod_filtered = hmrBandpassFilt(dod, 0.01, 0.5, rawData.fs);

% 4. 运动伪影检测与校正
[motionArtifact, motionIndex] = hmrMotionArtifact(dod_filtered, rawData.fs);
dod_corrected = hmrMotionCorrectWavelet(dod_filtered, motionIndex);

% 5. 剔除无效通道
dod_pruned = enPruneChannels(dod_corrected);

% 6. 光密度转浓度
conc = hmrOD2Conc(dod_pruned, rawData.ppf);

% 7. 剔除刺激相关伪影
conc_clean = enStimRejection(conc, rawData.stim);

% 8. 数据标准化
conc_normalized = zscore(conc_clean);

% 9. 试次截取与基线校正
% 假设 trials 是试次时间标记
trials = [start1, end1; start2, end2; ...];
baseline_window = 5 * rawData.fs; % 基线时间段（5秒）
conc_trials = hmrBlockAvg(conc_normalized, trials, baseline_window);

% 10. 数据可视化
plotTrials(conc_trials);

---

总结

通过以上步骤，您可以完成近红外数据的预处理，包括：

1. 数据导入与转换。
2. 噪声去除与运动伪影校正。
3. 通道筛选与数据标准化。
4. 试次截取与基线校正。

函数说明

function dod = hmrFlowInput( d )

for i = 1:size(d,2);
lst = find(isnan(d(:,i)));
d(lst,i) = nanmean(d(:,i));
clear lst
end

% percent change
dm = mean(abs(d),1);
nTpts = size(d,1);
dod = (abs(d)./(ones(nTpts,1)*dm));

if ~isempty(find(d(:)<=0))
    warning( 'WARNING: Some data points in d are zero or negative.' );
end

这个函数 hmrFlowInput 的主要用途是对输入的近红外光强度数据进行预处理，具体包括以下步骤：

---

1. 处理缺失值（NaN）

• 代码:

  for i = 1:size(d,2)
      lst = find(isnan(d(:,i)));
      d(lst,i) = nanmean(d(:,i));
      clear lst
  end
  

• 作用:
  • 检查每一列（通常是每个通道的光强度数据）是否存在缺失值（NaN）。
  • 如果存在缺失值，用该列的均值（忽略 NaN 计算）填充缺失值。
• 意义:
  • 确保数据中没有缺失值，避免后续计算出错。

---

2. 计算光强度的百分比变化

• 代码:

  dm = mean(abs(d),1);
  nTpts = size(d,1);
  dod = (abs(d)./(ones(nTpts,1)*dm));
  

• 作用:
  • 计算每个通道的光强度均值 dm。
  • 将每个通道的光强度数据除以其均值，得到百分比变化（dod，即光密度变化）。
• 意义:
  • 将光强度数据标准化为相对于均值的百分比变化，消除不同通道之间的基线差异。

---

3. 检查数据有效性

• 代码:

  if ~isempty(find(d(:)<=0))
      warning( 'WARNING: Some data points in d are zero or negative.' );
  end
  

• 作用:
  • 检查数据中是否存在零或负值。
  • 如果存在，发出警告提示。
• 意义:
  • 光强度数据应为正值，零或负值可能是数据采集错误或异常，需要进一步检查。

---

4. 输出结果

• 输出变量:
  • dod: 光密度变化数据，表示光强度相对于均值的百分比变化。

---

总结

这个函数的主要用途是对近红外光强度数据进行预处理，包括：

1. 处理缺失值（NaN）。
2. 计算光强度的百分比变化（光密度变化，dod）。
3. 检查数据中是否存在零或负值，并发出警告。

适用场景:

• 在近红外数据分析中，光强度数据通常需要转换为光密度变化（dod），以便后续分析（如计算血红蛋白浓度）。
• 这个函数是数据预处理的一部分，通常会在 hmrIntensity2OD 或其他光密度转换函数之前使用。

---

示例

假设输入数据 d 是一个矩阵，表示多个通道的光强度数据（每列是一个通道，每行是一个时间点）：

d = [100, 200, 300; 
     NaN, 210, 310; 
     110, 220, 320];
dod = hmrFlowInput(d);

输出 dod 是光密度变化数据，表示每个通道的光强度相对于其均值的百分比变化。
截取一部分时间点来观察处理后的图像