数据结构与算法面试分享(二十八)：分治算法

最新推荐文章于 2024-07-20 15:35:45 发布

之乎者也·

最新推荐文章于 2024-07-20 15:35:45 发布

阅读量397

点赞数 8

分类专栏：数据结构与算法文章标签：面试算法分治算法

本文链接：https://blog.csdn.net/qq_45038038/article/details/135195836

版权

数据结构与算法专栏收录该内容

33 篇文章 1 订阅

订阅专栏

刷题网站相关题目：

剑指51.数组中的逆序对【困难】169.多数元素【简单】53.最大子序和【简单】50.Pow(x,n)【中等】4.寻找两个正序数组的中位数【困难】932.漂亮数组【中等】514.自由之路【困难】903.DI 序列的有效排列【困难】327.区间和的个数【困难】...

一、汉诺塔问题

1.1、问题描述

汉诺塔问题是一个益智游戏，有三根杆子和一些圆盘，圆盘的大小各不相同，初始时所有圆盘都堆叠在一根杆子上，按照从上到下递减的顺序排列。游戏的目标是将所有圆盘从初始杆子移动到目标杆子，同时遵循以下规则：

每次只能移动一个圆盘。
大圆盘不能放在小圆盘上面。

1.2、解题思路

使用分治法来解决汉诺塔问题的思路如下：

如果只有一个圆盘（n=1），直接将它从初始杆子移动到目标杆子。
如果有多个圆盘（n>1），可以将问题分解为三个子问题：
1. 将n-1个圆盘从初始杆子移动到辅助杆子，借助目标杆子。
2. 将第n个圆盘从初始杆子移动到目标杆子。
3. 将n-1个圆盘从辅助杆子移动到目标杆子，借助初始杆子。

通过递归地解决这三个子问题，最终可以将所有圆盘从初始杆子移动到目标杆子，遵循汉诺塔问题的规则。

1.3、代码示例

下面是用C++实现的示例代码：

#include <iostream>
// 函数定义：将n个圆盘从source杆移动到target杆，借助auxiliary杆
void hanoi(int n, char source, char auxiliary, char target) {
    if (n == 1) {
        // 只有一个圆盘时，直接移动
        std::cout << "Move disk 1 from " << source << " to " << target << std::endl;
    } else {
        // 先将n-1个圆盘从source杆移动到auxiliary杆，借助target杆
        hanoi(n - 1, source, target, auxiliary);
        
        // 移动第n个圆盘
        std::cout << "Move disk " << n << " from " << source << " to " << target << std::endl;
        
        // 再将n-1个圆盘从auxiliary杆移动到target杆，借助source杆
        hanoi(n - 1, auxiliary, source, target);
    }
}

int main() {
    int n = 3; // 圆盘数量
    hanoi(n, 'A', 'B', 'C'); // 调用hanoi函数解决问题
    return 0;
}

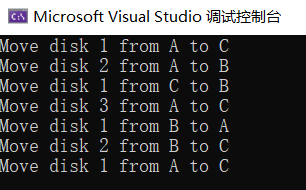
结果输出：

二、最大子数组和问题

2.1、问题描述

给定一个包含整数的数组 nums，我们需要找到一个连续的子数组，使得子数组的和最大。我们要求返回这个最大的子数组和。

2.2、解题思路

使用分治法解决最大子数组和问题的思路如下：

将原始数组分成两半：left 和 right。
递归地计算 left 和 right 子数组的最大子数组和，分别记为 leftMax 和 rightMax。
计算横跨左右两个子数组的最大子数组和。从数组中间开始向左右两边扩展，分别计算左边和右边的子数组的最大和。最后将这两个和相加，得到横跨的子数组的最大和，记为 crossMax。
最大子数组和要么在 leftMax、rightMax、crossMax 中，要么跨越左右两个子数组。因此，最终的最大子数组和是这三者中的最大值。

2.3、代码示例

#include <iostream>
#include <vector>
#include <algorithm>

int maxCrossingSum(std::vector<int>& nums, int left, int mid, int right) {
    int leftSum = INT_MIN;
    int sum = 0;
    
    for (int i = mid; i >= left; --i) {
        sum += nums[i];
        leftSum = std::max(leftSum, sum);
    }
    
    int rightSum = INT_MIN;
    sum = 0;
    
    for (int i = mid + 1; i <= right; ++i) {
        sum += nums[i];
        rightSum = std::max(rightSum, sum);
    }
    
    return leftSum + rightSum;
}

int maxSubarraySum(std::vector<int>& nums, int left, int right) {
    if (left == right) {
        return nums[left];
    }
    
    int mid = (left + right) / 2;
    
    int leftMax = maxSubarraySum(nums, left, mid);
    int rightMax = maxSubarraySum(nums, mid + 1, right);
    int crossMax = maxCrossingSum(nums, left, mid, right);
    
    return std::max({leftMax, rightMax, crossMax});
}

int maxSubArray(std::vector<int>& nums) {
    if (nums.empty()) {
        return 0;
    }
    
    int left = 0;
    int right = nums.size() - 1;
    
    return maxSubarraySum(nums, left, right);
}

int main() {
    std::vector<int> nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
    int result = maxSubArray(nums);
    std::cout << "Maximum subarray sum: " << result << std::endl;
    
    return 0;
}

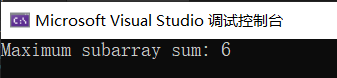
结果输出：

三、最接近点对问题

3.1、问题描述

最接近点对问题是一个计算几何学问题，它要求在一个平面上给定一组点，找到其中最接近的两个点对（点对之间的距离最小）。

给定平面上的一组点 P = {p1, p2, ..., pn}，其中每个点 pi 都有一个二维坐标 (xi, yi)，我们需要找到一对点 (p_i, p_j) 使得它们之间的欧氏距离 ||pi - pj|| 最小。

3.2、解题思路

首先，对点集 P 按照 x 坐标进行排序，得到一个按 x 坐标递增排列的点集 Px。同时，对点集 P 按照 y 坐标进行排序，得到一个按 y 坐标递增排列的点集 Py。
利用分治法，将点集 Px 分成两部分：左半部分 Pl 和右半部分 Pr，同时也将点集 Py 分成相应的左半部分 Ql 和右半部分 Qr。
递归地在左半部分 Pl 和 Pr 中分别寻找最接近点对（使用相同的算法），得到左半部分的最近点对 d1 和右半部分的最近点对 d2。
找到两个最近点对 d1 和 d2 中距离较小的那一个，记为 delta。
然后，检查以 delta 距离内的所有点，查看是否有更近的点对。这一步可以在 Px 和 Py 中同时进行，因为我们只需要考虑在 delta 范围内的点。
最后，返回最接近点对的距离。

3.3、代码示例

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <limits>

// 定义一个点的结构体
struct Point {
    double x;
    double y;
};

// 按照 x 坐标进行比较的比较函数
bool compareX(const Point& p1, const Point& p2) {
    return p1.x < p2.x;
}

// 按照 y 坐标进行比较的比较函数
bool compareY(const Point& p1, const Point& p2) {
    return p1.y < p2.y;
}

// 计算两点之间的欧氏距离
double euclideanDistance(const Point& p1, const Point& p2) {
    double dx = p1.x - p2.x;
    double dy = p1.y - p2.y;
    return sqrt(dx * dx + dy * dy);
}

// 求解最接近点对的函数
double closestPairUtil(std::vector<Point>& Px, std::vector<Point>& Py, int left, int right) {
    if (right - left <= 2) {
        // 如果点数小于等于3，直接暴力计算最近点对距离
        double minDistance = std::numeric_limits<double>::max();
        for (int i = left; i < right; ++i) {
            for (int j = i + 1; j < right; ++j) {
                minDistance = std::min(minDistance, euclideanDistance(Px[i], Px[j]));
            }
        }
        return minDistance;
    }
    
    // 将 Px 和 Py 分成左右两部分
    int mid = (left + right) / 2;
    
    std::vector<Point> Plx(Px.begin() + left, Px.begin() + mid);
    std::vector<Point> Prx(Px.begin() + mid, Px.begin() + right);
    
    std::vector<Point> Ply, Pry;
    
    double midX = Px[mid].x;
    
    for (const Point& p : Py) {
        if (p.x < midX) {
            Ply.push_back(p);
        } else {
            Pry.push_back(p);
        }
    }
    
    // 递归地计算左右两部分的最近点对距离
    double delta1 = closestPairUtil(Plx, Ply, 0, mid - left);
    double delta2 = closestPairUtil(Prx, Pry, 0, right - mid);
    
    double delta = std::min(delta1, delta2);
    
    // 查找跨越两个子数组的最近点对
    std::vector<Point> strip;
    for (const Point& p : Py) {
        if (fabs(p.x - midX) < delta) {
            strip.push_back(p);
        }
    }
    
    // 在 strip 中查找最近点对
    int stripSize = strip.size();
    for (int i = 0; i < stripSize; ++i) {
        for (int j = i + 1; j < stripSize && (strip[j].y - strip[i].y) < delta; ++j) {
            delta = std::min(delta, euclideanDistance(strip[i], strip[j]));
        }
    }
    
    return delta;
}

// 计算最接近点对的主函数
double closestPair(std::vector<Point>& points) {
    int n = points.size();
    
    // 将点按照 x 坐标进行排序
    std::vector<Point> Px = points;
    std::sort(Px.begin(), Px.end(), compareX);
    
    // 将点按照 y 坐标进行排序
    std::vector<Point> Py = points;
    std::sort(Py.begin(), Py.end(), compareY);
    
    return closestPairUtil(Px, Py, 0, n);
}

int main() {
    std::vector<Point> points = {{1, 2}, {3, 4}, {5, 6}, {7, 8}, {9, 10}};
    
    double minDistance = closestPair(points);
    
    std::cout << "最接近点对的距离是：" << minDistance << std::endl;
    
    return 0;
}

首先对点集按照 x 坐标和 y 坐标分别排序，然后通过递归的方式找到最近点对的距离。在找到最近点对的过程中，还考虑了跨越左右两个子数组的情况。

结果输出：

四、矩阵乘法问题

4.1、问题描述

给定两个矩阵 A 和 B，我们的任务是计算它们的乘积 C，其中 C = A * B。矩阵的乘法规则是：C 的每个元素 C[i][j] 等于 A 的第 i 行与 B 的第 j 列对应元素的乘积之和。

4.2、解题思路

将两个矩阵 A 和 B 分别划分成四个子矩阵，分别记为 A11、A12、A21、A22 以及 B11、B12、B21、B22。这个划分可以通过将原始矩阵分成四个等大小的子矩阵来实现。
使用递归的方式计算子矩阵的乘积，即计算 P1 = A11 * (B12 - B22)，P2 = (A11 + A12) * B22，P3 = (A21 + A22) * B11，P4 = A22 * (B21 - B11)，P5 = (A11 + A22) * (B11 + B22)，P6 = (A12 - A22) * (B21 + B22)，P7 = (A11 - A21) * (B11 + B12)。
利用这些子问题的解 P1 到 P7，计算矩阵 C 的四个子矩阵：C11 = P5 + P4 - P2 + P6，C12 = P1 + P2，C21 = P3 + P4，C22 = P5 + P1 - P3 - P7。
最后，将这些子矩阵合并成矩阵 C，即 C = [C11, C12; C21, C22]。

4.3、代码示例

#include <iostream>
#include <vector>

// 函数用于将两个矩阵相加
std::vector<std::vector<int>> matrixAdd(const std::vector<std::vector<int>>& A, const std::vector<std::vector<int>>& B) {
    int n = A.size();
    int m = A[0].size();
    std::vector<std::vector<int>> result(n, std::vector<int>(m));

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            result[i][j] = A[i][j] + B[i][j];
        }
    }

    return result;
}

// 函数用于将两个矩阵相减
std::vector<std::vector<int>> matrixSubtract(const std::vector<std::vector<int>>& A, const std::vector<std::vector<int>>& B) {
    int n = A.size();
    int m = A[0].size();
    std::vector<std::vector<int>> result(n, std::vector<int>(m));

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            result[i][j] = A[i][j] - B[i][j];
        }
    }

    return result;
}

// 函数用于分治矩阵乘法
std::vector<std::vector<int>> matrixMultiply(const std::vector<std::vector<int>>& A, const std::vector<std::vector<int>>& B) {
    int n = A.size();

    // 如果矩阵大小为1x1，则直接相乘
    if (n == 1) {
        std::vector<std::vector<int>> result(1, std::vector<int>(1));
        result[0][0] = A[0][0] * B[0][0];
        return result;
    }

    // 将矩阵分为四个子矩阵
    int half_size = n / 2;
    std::vector<std::vector<int>> A11(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> A12(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> A21(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> A22(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> B11(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> B12(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> B21(half_size, std::vector<int>(half_size));
    std::vector<std::vector<int>> B22(half_size, std::vector<int>(half_size));

    // 将输入矩阵分割为子矩阵
    for (int i = 0; i < half_size; ++i) {
        for (int j = 0; j < half_size; ++j) {
            A11[i][j] = A[i][j];
            A12[i][j] = A[i][j + half_size];
            A21[i][j] = A[i + half_size][j];
            A22[i][j] = A[i + half_size][j + half_size];

            B11[i][j] = B[i][j];
            B12[i][j] = B[i][j + half_size];
            B21[i][j] = B[i + half_size][j];
            B22[i][j] = B[i + half_size][j + half_size];
        }
    }

    // 递归计算子矩阵的乘积
    std::vector<std::vector<int>> P1 = matrixMultiply(A11, matrixSubtract(B12, B22));
    std::vector<std::vector<int>> P2 = matrixMultiply(matrixAdd(A11, A12), B22);
    std::vector<std::vector<int>> P3 = matrixMultiply(matrixAdd(A21, A22), B11);
    std::vector<std::vector<int>> P4 = matrixMultiply(A22, matrixSubtract(B21, B11));
    std::vector<std::vector<int>> P5 = matrixMultiply(matrixAdd(A11, A22), matrixAdd(B11, B22));
    std::vector<std::vector<int>> P6 = matrixMultiply(matrixSubtract(A12, A22), matrixAdd(B21, B22));
    std::vector<std::vector<int>> P7 = matrixMultiply(matrixSubtract(A11, A21), matrixAdd(B11, B12));

    // 计算结果矩阵的四个分块
    std::vector<std::vector<int>> C11 = matrixAdd(matrixSubtract(matrixAdd(P5, P4), P2), P6);
    std::vector<std::vector<int>> C12 = matrixAdd(P1, P2);
    std::vector<std::vector<int>> C21 = matrixAdd(P3, P4);
    std::vector<std::vector<int>> C22 = matrixAdd(matrixSubtract(matrixAdd(P5, P1), P3), P7);

    // 合并结果矩阵
    std::vector<std::vector<int>> result(n, std::vector<int>(n));
    for (int i = 0; i < half_size; ++i) {
        for (int j = 0; j < half_size; ++j) {
            result[i][j] = C11[i][j];
            result[i][j + half_size] = C12[i][j];
            result[i + half_size][j] = C21[i][j];
            result[i + half_size][j + half_size] = C22[i][j];
        }
    }

    return result;
}

int main() {
    // 示例矩阵 A 和 B
    std::vector<std::vector<int>> A = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}, {13, 14, 15, 16}};
    std::vector<std::vector<int>> B = {{17, 18, 19, 20}, {21, 22, 23, 24}, {25, 26, 27, 28}, {29, 30, 31, 32}};

    // 计算矩阵乘积
    std::vector<std::vector<int>> result = matrixMultiply(A, B);

    // 打印结果
    int n = result.size();
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            std::cout << result[i][j] << " ";
        }
        std::cout << std::endl;
    }

    return 0;
}

矩阵分为四个子矩阵，递归计算子矩阵的乘积，然后将它们组合成最终的结果矩阵

结果输出：

五、多项式乘法问题

5.1、问题描述

给定两个多项式：

A(x) = a_n * x^n + a_(n-1) * x^(n-1) + ... + a_1 * x^1 + a_0B(x) = b_m * x^m + b_(m-1) * x^(m-1) + ... + b_1 * x^1 + b_0

其中，n 和 m 分别表示多项式 A 和 B 的次数。要求计算它们的乘积：

C(x) = A(x) * B(x)

5.2、解题思路

将多项式 A 和 B 均分为两部分，得到：

A(x) = A0(x) + A1(x)B(x) = B0(x) + B1(x)

递归计算四个子问题：

C0(x) = A0(x) * B0(x)C1(x) = A0(x) * B1(x)C2(x) = A1(x) * B0(x)C3(x) = A1(x) * B1(x)

计算结果多项式 C(x) 的系数，其中：

C(x) = C0(x) * x^(n/2) + C1(x) * x^(n/2) + C2(x) * x^(n/2) + C3(x)

5.3、代码示例

#include <iostream>
#include <vector>

// 函数用于将两个多项式相乘
std::vector<int> polynomialMultiply(const std::vector<int>& A, const std::vector<int>& B) {
    int n = A.size();
    int m = B.size();

    // 如果多项式的长度为1，则直接相乘
    if (n == 1 || m == 1) {
        std::vector<int> result(n + m - 1, 0);
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                result[i + j] += A[i] * B[j];
            }
        }
        return result;
    }

    // 将多项式 A 和 B 分为两部分
    int half = std::max(n, m) / 2;
    std::vector<int> A0(A.begin(), A.begin() + std::min(half, n));
    std::vector<int> A1(A.begin() + std::min(half, n), A.end());
    std::vector<int> B0(B.begin(), B.begin() + std::min(half, m));
    std::vector<int> B1(B.begin() + std::min(half, m), B.end());

    // 递归计算四个子问题
    std::vector<int> C0 = polynomialMultiply(A0, B0);
    std::vector<int> C2 = polynomialMultiply(A1, B1);

    // 计算中间多项式 D(x) = (A0 + A1)(B0 + B1) - C0 - C2
    std::vector<int> D(n + m - 1, 0);
    std::vector<int> A0A1(A0);
    A0A1.insert(A0A1.end(), A1.begin(), A1.end());
    std::vector<int> B0B1(B0);
    B0B1.insert(B0B1.end(), B1.begin(), B1.end());
    std::vector<int> C1 = polynomialMultiply(A0A1, B0B1);
    for (int i = 0; i < n + m - 1; ++i) {
        D[i] = C1[i] - C0[i] - C2[i];
    }

    // 合并结果
    std::vector<int> result(n + m - 1, 0);
    for (int i = 0; i < n + m - 1; ++i) {
        result[i] = C0[i] + D[i] * (1 << half) + C2[i] * (1 << (2 * half));
    }

    return result;
}

int main() {
    // 示例多项式 A 和 B 的系数
    std::vector<int> A = {1, 2, 3};
    std::vector<int> B = {4, 5, 6};

    // 计算多项式乘积
    std::vector<int> result = polynomialMultiply(A, B);

    // 打印结果
    for (int i = 0; i < result.size(); ++i) {
        std::cout << result[i];
        if (i < result.size() - 1) {
            std::cout << "x^" << i << " + ";
        }
    }

    return 0;
}

六、寻找中位数问题

6.1、问题描述

给定一个包含整数的无序数组，找出该数组的中位数。中位数是指将数组按升序排列后，位于数组中间的那个数。如果数组有偶数个元素，则中位数是中间两个数的平均值。

6.2、解题思路

选择数组中的一个元素作为"枢轴"（pivot）。
将数组中小于枢轴的元素放在枢轴的左边，将大于枢轴的元素放在枢轴的右边。这个过程叫做分区（partition）。
如果枢轴的位置恰好是数组的中间位置（即，它的左边有 n/2 个元素，右边也有 n/2 个元素），那么枢轴就是中位数，直接返回。
如果枢轴的位置在中位数的左边（即，它的左边有 n/2 个元素，右边有 n/2+1 个元素），那么中位数必然在枢轴的右边，递归地在右半部分查找中位数。
如果枢轴的位置在中位数的右边（即，它的左边有 n/2+1 个元素，右边有 n/2 个元素），那么中位数必然在枢轴的左边，递归地在左半部分查找中位数。

这个算法的关键是每次分区都能将枢轴放在中位数的位置上，从而不断缩小查找范围，最终找到中位数。

6.3、代码示例

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int partition(vector<int>& nums, int left, int right) {
    int pivot = nums[right]; // 选择最右边的元素作为枢轴
    int i = left - 1; // 左边界的前一个位置

    for (int j = left; j < right; j++) {
        if (nums[j] <= pivot) {
            i++;
            swap(nums[i], nums[j]);
        }
    }

    swap(nums[i + 1], nums[right]); // 将枢轴放在正确的位置
    return i + 1;
}

int findMedian(vector<int>& nums, int left, int right, int k) {
    if (left == right) {
        return nums[left];
    }

    int pivotIndex = partition(nums, left, right);
    int count = pivotIndex - left + 1;

    if (count == k) {
        return nums[pivotIndex];
    } else if (count < k) {
        return findMedian(nums, pivotIndex + 1, right, k - count);
    } else {
        return findMedian(nums, left, pivotIndex - 1, k);
    }
}

double findMedian(vector<int>& nums) {
    int n = nums.size();
    if (n % 2 == 0) {
        int median1 = findMedian(nums, 0, n - 1, n / 2);
        int median2 = findMedian(nums, 0, n - 1, n / 2 + 1);
        return (static_cast<double>(median1) + static_cast<double>(median2)) / 2.0;
    } else {
        return findMedian(nums, 0, n - 1, n / 2 + 1);
    }
}

int main() {
    vector<int> nums = {3, 1, 4, 2, 5};
    double median = findMedian(nums);
    cout << "Median: " << median << endl;
    return 0;
}

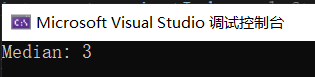
时间复杂度：O(n)

结果输出：

七、最近邻问题

7.1、问题描述

给定平面上的一组点，找到其中最近的两个点。这个问题通常被称为最近邻问题（Nearest Neighbor Problem）。在二维平面上，我们可以使用欧几里得距离来度量两点之间的距离。

7.2、解题思路

将平面上的点分成两部分，然后递归地找到每一部分中的最近邻点，最后再比较这两个部分中的最近邻点，取距离最小的那一对点。

具体步骤如下：

如果点的数量小于等于3个（或其他合适的小规模），直接计算它们之间的距离并返回最小的距离对。
如果点的数量大于3个，将点集分成两部分，分别处理左边和右边的子集。
递归地找到左边子集和右边子集中的最近邻点对，分别记为(d1, p1)和(d2, p2)。
计算左边子集和右边子集之间的最短距离，记为d。
如果d1小于d2，则最近邻点对是(d1, p1)；否则，最近邻点对是(d2, p2)。
最后，需要考虑跨越左右两个子集的最近邻点对，这个距离不会超过d。

7.3、代码示例

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#include <limits>

using namespace std;

struct Point {
    double x, y;
};

bool compareX(const Point& p1, const Point& p2) {
    return p1.x < p2.x;
}

bool compareY(const Point& p1, const Point& p2) {
    return p1.y < p2.y;
}

double euclideanDistance(const Point& p1, const Point& p2) {
    double dx = p1.x - p2.x;
    double dy = p1.y - p2.y;
    return sqrt(dx * dx + dy * dy);
}

pair<Point, Point> closestPair(vector<Point>& points, int left, int right) {
    if (right - left <= 3) {
        double minDistance = numeric_limits<double>::max();
        pair<Point, Point> closest;
        for (int i = left; i < right; i++) {
            for (int j = i + 1; j < right; j++) {
                double dist = euclideanDistance(points[i], points[j]);
                if (dist < minDistance) {
                    minDistance = dist;
                    closest = {points[i], points[j]};
                }
            }
        }
        return closest;
    }

    int mid = (left + right) / 2;
    pair<Point, Point> leftClosest = closestPair(points, left, mid);
    pair<Point, Point> rightClosest = closestPair(points, mid, right);

    double minDistance = min(euclideanDistance(leftClosest.first, leftClosest.second),
                             euclideanDistance(rightClosest.first, rightClosest.second));

    vector<Point> strip;
    for (int i = left; i < right; i++) {
        if (abs(points[i].x - points[mid].x) < minDistance) {
            strip.push_back(points[i]);
        }
    }

    sort(strip.begin(), strip.end(), compareY);

    for (int i = 0; i < strip.size(); i++) {
        for (int j = i + 1; j < strip.size() && strip[j].y - strip[i].y < minDistance; j++) {
            double dist = euclideanDistance(strip[i], strip[j]);
            if (dist < minDistance) {
                minDistance = dist;
                leftClosest = {strip[i], strip[j]};
            }
        }
    }

    return min(leftClosest, rightClosest);
}

pair<Point, Point> findClosestPair(vector<Point>& points) {
    sort(points.begin(), points.end(), compareX);
    return closestPair(points, 0, points.size());
}

int main() {
    vector<Point> points = {{0, 0}, {1, 1}, {2, 2}, {3, 3}, {4, 4}};
    pair<Point, Point> closest = findClosestPair(points);
    cout << "Closest pair: (" << closest.first.x << ", " << closest.first.y << ") and ("
         << closest.second.x << ", " << closest.second.y << ")" << endl;
    return 0;
}

时间复杂度：n(nlogn)

之乎者也·

关注

8
点赞
踩
7

收藏

觉得还不错? 一键收藏
打赏
0
评论
数据结构与算法面试分享(二十八)：分治算法

使用递归的方式计算子矩阵的乘积，即计算 P1 = A11 * (B12 - B22)，P2 = (A11 + A12) * B22，P3 = (A21 + A22) * B11，P4 = A22 * (B21 - B11)，P5 = (A11 + A22) * (B11 + B22)，P6 = (A12 - A22) * (B21 + B22)，P7 = (A11 - A21) * (B11 + B12)。将数组中小于枢轴的元素放在枢轴的左边，将大于枢轴的元素放在枢轴的右边。
复制链接

扫一扫