三种背包问题+滚动数组优化

三种背包问题+滚动数组优化

滚动数组

滚动数组简单的理解就是让数组滚动起来，起到节省存储空间的作用。主要应用在递推或动态规划中。

举个适合使用滚动数组的例子:
斐波那契数列为1、1、2、3、5、8、13、21、34……此数列从第3项开始，每一项都等于前两项之和。
递推公式为F(n)=F(n-1)+F(n-2)，n≥3，F(1)=1，F(2)=1。

假如我们要求斐波拉切数列的第80项，我们常规的方法是定义一个80大小的数组，然后进行如下的循环。

那么我们要求第2e7项的斐波拉契，我们不可能去定义一个2e7的数组。通过观察，我们可以发现其实每一次循环都只用到前两位的数组，使用过后就不会使用了，很浪费空间。我们可以使用滚动数组来解决。

使用滚动数组的话，我们就只需要定义一个3大小的数组(仔细想想我们滚动话只需要3个数就够了)。

滚动数组的使用重在对于取余(%)的理解下面来演示一下。

无论多大的数取余某个数时，得到的数都在0到这个数之间。当下标对循环长度取余，则对于n长度的环，第n-1个的下一个将会是第0个，从而实现了循环。

滚动数组只能节约空间复杂度，时间复杂度还是和原来一样。

01背包

描述:
有n件物品和一个容量为m的背包。第i件物品的费用是v[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。

状态转移方程:

二维数组

用 dp[i][j]表示前i种物品放入一个容量为j的背包的最大价值
dp[i][j]=j<w[i]? dp[i-1][j]:max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]); (1<=i<=n,0<=j<=m)

下面通过图表样例理解下




此时我们可以发现我们得到了这么一个数组，dp[i][j]即表示在前i个物品中选取任意物品装填承重j背包时可得到的最大价值和。

通过对上面图表的分析理解我们发现，我们只需要前两行的值就能得出新的一行，和斐波拉契很相似，我们可以使用滚动数组。

滚动数组

代码解析:

但是仅仅滚动数组的优化通常来说是不够的。毕竟不管怎么样还是一个二维数组，优化始终是有限的。

优化版

用dp[j]表示当前总重量为j的所有方案中的最大价值
dp[j]=max(dp[j],dp[j-w[i]]+v[i]); (1<=i<=n ,w[i]<=j<=W)

代码解析:

这里的一维数组的优化是最优的。

核心是基于一维数组做反向迭代，这样的话j<w[i]的部分直接不用复制了，且由于是反向的线性更新也不会发生冲突。

举个例子

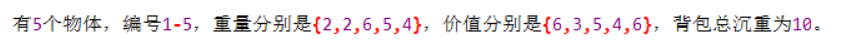
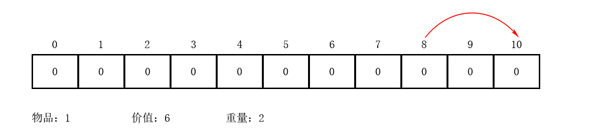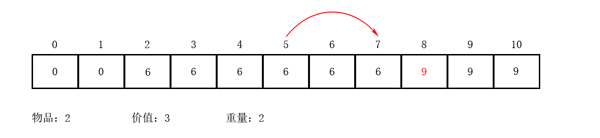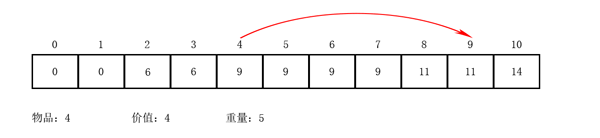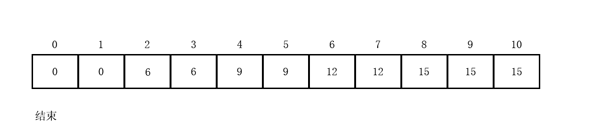
结合动图理解这里的反向迭代的巧妙。

完全背包

描述:
N种物品，第i种的物品重量是w[i],价值是v[i]，每种物品有无限件，求总重量在背包承重m以内的最大总价值。

状态转移方程:

二维数组

用dp[i][j]表示前i种物品放入一个容量为j的背包的最大价值类似于简化为01背包。
dp[i][j] = max(dp[i][j], dp[i-1][j-kw[i]] + kv[i]]) (1<=i<=n,0<=j<=m) (0 <= k*w[i] <= j)

代码解析:

这里可以理解为变相的01背包，重量为kw[i],价值为kv[i]。

小优化版:用dp[i][j]表示前i种物品放入一个容量为j的背包的最大价值,
dp[i][j] = max(dp[i-1][j],dp[i][j-w[i]+v[i]) (1<=i<=n,0<=j<=W)

代码解析:

核心在于将已装载的dp[i][j]用于后续dp，因为物品无限件，同一物品可以选取多次。这是其与01背包的主要区别。

01背包 dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
完全背包 dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);

这个已装载怎么理解？
举个例子:
遍历到第5个物品，其重量是3：
那么dp[5][3]处在此次迭代中会存: 以3容量的背包选取前4种物品 和 选取一个桃子后以0容量的背包选取前四种物品中的最优情况。dp[i][j]=max(dp[i-1][j],dp[i][j-w[i]]+v[i]);

如果此时选择第5个的情况是最优情况，被存储了，那就表示已装载。因为能在后续的遍历中多次拿到第5个物品。

如果已经dp[5][3]拿到了第5个物品那么在后续的dp[5][6]只需要存: 以6容量的背包选取前4种物品 和 再拿一个第5个物品加上dp[5][3]中的最优情况。

---

看一下和01背包的区别
在01背包中：
假如遍历到第5个物品，其重量是3：
那么dp[5][3]在此处迭代会存:以3容量的背包选取前4种物品 和 选取一个桃子后以0容量的背包选取前四种物品中的最优情况。dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
而dp[5][6]则是存以6容量的背包选取前4种物品 和 (以3容量的背包选取前4种物品+一个第5中物品的价值)的最优情况。
dp[5][6]与dp[5][3]没有直接的迭代关系。

滚动数组

完全背包的滚动数组和01背包类似。

代码解析:

但是仅仅滚动数组的优化通常来说是不够的。

优化版

用dp[j]表示当前总重量为j的所有方案中的最大价值
dp[j]=max(dp[j],dp[j-w[i]]+v[i]); (1<=i<=n,0<=j<=W)

代码解析:

核心在于类似01背包的反向迭代

举个例子

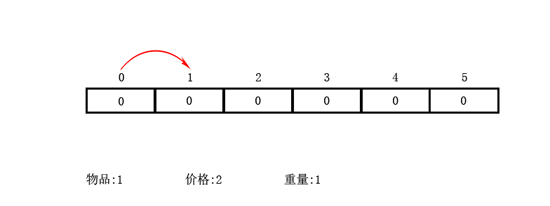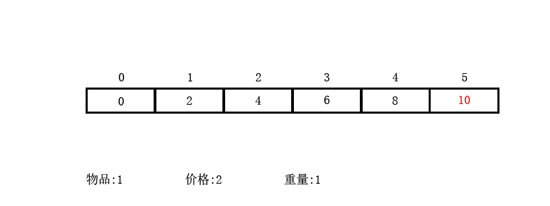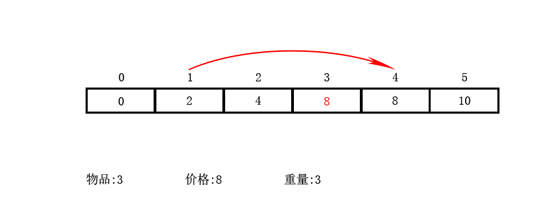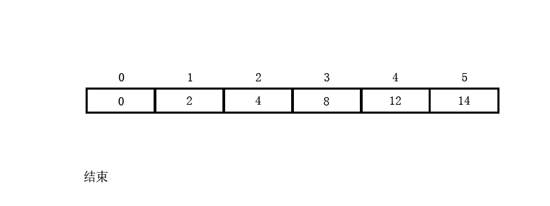
结合01背包的动图，理解其区别。

多重背包

描述
有n种物品，第i种物品的重量是w[i],价值是w[i],每种物品的数量有限k[i],如何在m重量内，让总价值尽可能最大。

普通的二维解法和完全背包很类似。

二维数组

代码解析:

这里与完全背包唯一不同的就是不但要满足背包大小，还要满足物品个数。

滚动数组

滚动数组多重背包

代码解析:

二进制优化

这里三个for循环复杂度太高，不适合很多题目，我们要进行优化。

首先我们要知道我们的目的是什么，目的是将单种物品分解为概念上的多个不同物品然后做01背包。而且分解不是乱分解的，我们需要做到首先不能重复，其次需要将所有的分解的情况都要表示出来，比如有10个x物品，我们需要把0-10的组合情况全部都能表示出来。

优化解法 (二进制优化)
1.如果限制的数量*物品容量>=当前最大容量
直接考虑成完全背包问题来处理，把物品数量当成无限数量来考虑。

2.如果限制的数量物品容量<当前最大容量
将单种物品二进制分解为概念上的多个不同物品然后做01背包*

普通情况直接完全背包很好理解，特殊的二进制分解我们可以根据例子来理解:

假如给了我们 价值为 2，但是数量却是10 的物品，我们应该把10给拆开，要知道二进制能够表示任何数的，所以10 就是可以有1,2,4,8之内的数把它组成，一开始我们选上 1了，然后让10-1=9，再选上2，9-2=7，在选上 4，7-4=3，而这时的3<8了，所以我们就是可以得出 10由 1,2,4,3来组成。

我们能发现1,2,3,4能组成1-10以内的任何数。

那么他们的价值是什么呢，是2,4,6,8，也就说给我们的价值为2，数量是10的这批货物，已经转化成了价值分别是2,4,6,8元的货物了，那么最后在进行dp选择的时候，就能通过他们的最优解选择，组成出我们需要的组成物品。形成概念上的01背包。