概率论与数理统计
- 引言
- ``第一章``
- 一、随机试验与随机事件
- 二、样本空间与事件的集合表示
- 三、事件间的关系
- 四、概率的初等描述
- 五、古典概型
- 七、几何概率模型
- 八、频率与概率
- 九、公理化
- 十、条件概率
- 十一、乘法公式
- 十二、全概率模型
- 十二、贝叶斯公式
- 十三、事件的独立性
- 十四、伯努利模型
- ``第二章``
- 一、随机变量的概念
- 二、离散型随机变量及其概率分布
- 三、连续性随机变量及其概率密度函数
- 四、分布函数
- 五、离散型的分布函数
- 六、连续型的分布函数
- 七、0-1分布
- 六、几何分布
- 七、二项分布(X~B(n,p))
- 八、泊松分布(X~P(λ))
- 九、超几何分布
- 十、均匀分布(X~U[a,b])
- 十一、指数分布
- 十二、正态分布
- 十三、随机变量函数的分布(离散型)
- 十四、随机变量函数的分布(连续型)
- ``第三章``
- 一、二维随机变量及其分布函数
- 二、二维连续型的联合分布与边缘分布
- 三、二维连续型随机变量的边缘密度函数
- 四、条件分布的定义
- 五、离散型随机变量的条件分布
- 六、连续型随机变量的条件分布
- 七、随机变量的独立性
- 八、二维离散型随机变量函数的分布
- 九、二维连续型随机变量函数的分布
- ``第四章``
- 一、离散型变量的数学期望
- 二、连续型变量的数学期望
- 三、随机变量函数的数学期望
- 四、数学期望的性质
- 五、条件期望
- 六、方差的定义
- 七、方差的性质
- 八、常见离散型的期望与方差
- 九、常见连续型的期望与方差
- 十、协方差
- 十一、相关系数
- 十二、中心矩与原点矩
引言
确定性(必然)现象:一定发生
随机(偶然)现象:可能发生
统计规律:做大量重复实验,试图找出某种规律
第一章
一、随机试验与随机事件
-
随机实验 E :
(1)在相同的条件下可重复
(2)实验结果不止一个
(3)无法预测出现什么结果 -
事件:实验的结果
随机事件:可能发生的实验结果 -
基本事件:相对于实验目的不能(不必)再分
【投掷硬币只需观察正反,不观察落地的坐标】 -
复合事件:由基本事件复合
【例子:骰子小于4的事件】 -
必然事件 Ω:一定发生的
不可能事件 :一定不发生
二、样本空间与事件的集合表示
-
样本空间 Ω:所有基本事件的集合
-
样本点 :样本空间的元素
平面内扔一个质子:Ω={(x,y)|x,y∈R}
- 事件的集合表示:
骰子不大于3的事件表示:C={1,2}

三、事件间的关系
- 包含

任意事件满足:Ø⊂A⊂Ω
-
相等
A⊂B且B⊂A -->A=B -
并(和)
A∪B、A+B
A与B至少有一个发生
A⊂A+B
A+A=A
A+Ø=A
A+Ω=Ω
- 交(积)
A∩B、AB
A与B同时发生
AB⊂A
AA=A
AØ=Ø
AΩ=A
- 差
A-B
A发生而B不发生
属于A不属于B
- 互不相容事件
A,B不同时发生,AB=Ø
n个事件A1、A2……An互不相容:
AiAj = Ø
- 对立事件
A与B互不相容,且A∪B=Ω

对立事件可称为对方的逆。
AB=Ø,且A+B=Ω
(1)
(2)
互不相容与对立区别:
(1)两事件对立,则一定是互不相容的
(2)互不相容适用于多个事件,对立对应于2个事件
(3)互不相容事件不能同时发生,可以都不发生。对立事件有且仅有一个发生
-
完备事件组
A1A2……An两两互不相容,且A1 ~ An的并为Ω
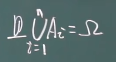
-
运算律

-
例子:

四、概率的初等描述
-
概率:事件A发生的大小。P(A)
-
性质 :
(1)P(Ω)=1
(2)P(Ø)=0
(3)0≤P(A)≤1
五、古典概型
-
条件:
(1)有限个样本点
(2)样本点等可能性 -
P(A)=A的有利样本点/Ω中样本点数=A中包含的基本事件数/基本事件总数
-
排列组合
(1)加法原理:做某事有几种方案
(2)乘法原理:做某事分几步
不重复排列:从n个不同元素中取出m个不同排列
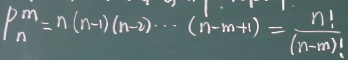
-
全排列:
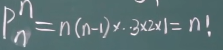
0!=1
-
重复排列:从n个不同元素中取m个排列
n * n*n……*n=nm -
组合:从n个不同元素中取出m个不同元素
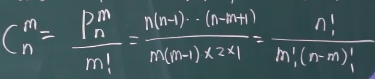
-
例子:

-
古典概率模型性质:
(1)非负性 0≤P(A)≤1
(2)规范性 P(Ω)=1 P(Ø)=0
(3)有限可加
(4)等概率
七、几何概率模型
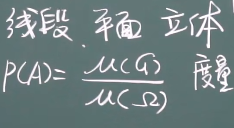
- 蒲风投针
长度为l的针(l<d),投掷到宽为d的两平行线中,与平行线相交的概率?
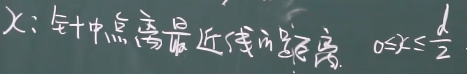
满足上述x才存在相交可能性,
还需要考虑角度

所以该事件得全局是
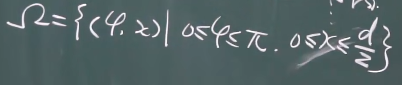
如何才能相交?
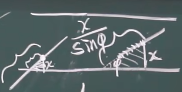
当斜边比l一半小才能相交,所以相交的情况满足下述条件
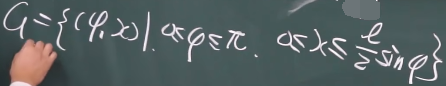
求G在Ω中的面积即可:
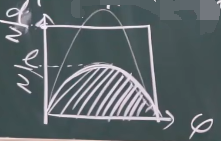
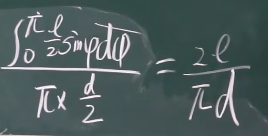
- 几何概率模型具有完全可加性
八、频率与概率
-
频率:
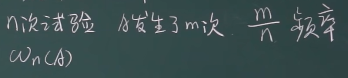
-
频率性质:
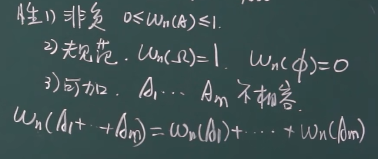
-
频率接近于一个值,这个值就叫做统计概率
九、公理化
-
公理一:(非负)0≤P(A)≤1
公理二:(规范)P(Ω)=1
公理三:(完全可加)A1A2……An互不容,P(A1+A2+……+An)=P(A1)+P(A2)+……+P(An) -
性质一:P(Ø)=0
性质二:有限相加,A1A2……An互不容,P(A1+A2+……+An)=P(A1)+P(A2)+……+P(An)
性质三:
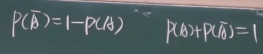
推论:A1A2……An完备事件组,P(Ω)=P(A1+A2+……+An)=P(A1)+P(A2)+……+P(An)=1
性质四:
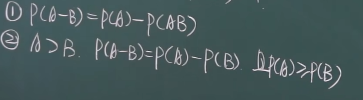
性质五:(加法)P(A+B)=P(A)+P(B)-P(AB)
P(A+B+C)=P(A)+P(B)+P©-P(AB)-P(AC)-P(BC)+P(ABC)
十、条件概率
-
例子:在吃到月饼情况下的概率

-
条件概率定义:Ω样本空间中,有A与B两个事件,P(B)>0。在B发生的条件下A发生的概率,既A对B的条件概率:P(A|B)。

-
计算条件概率
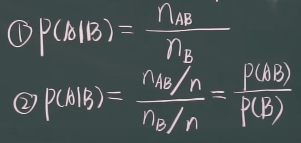
-
性质
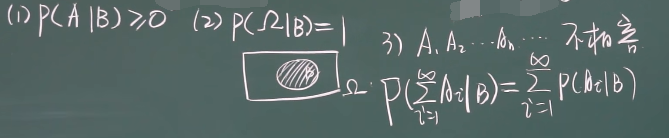
十一、乘法公式
P(AB) = P(B)*P(A|B)
P(AB) = P(A)*P(B|A)
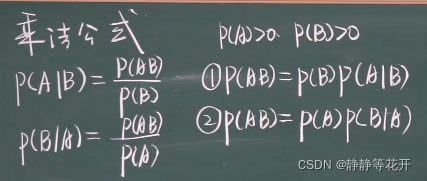
公式解释;
P(AB) = P(B)*P(A|B)
事件A和事件B同时发生的概率=事件B发生的概率 x 事件B发生下A发生的概率看成闯关:
A、B两关都过的概率 = 先过B关的概率 * 过了B关再过A关的概率
扩:
P(A1A2……An) = P(A1)P(A2|A1)P(A3|A1A2)……P(An|A1……An-1)
P(ABC) = P(A)P(B|A)P(C|AB)
例子:
产品100件,次品率是10%,不放回第三次才取到合格品的概率。
解:(┐表示非)
A1、A2、A3表示第1、2、3次取合格产品(┐A表示取到不合格产品)
P(┐A1 ┐A2 A3) = P(┐A1)P(┐A2|┐A1)P(A3|┐A2┐A1)=10/100 x 9/99 x 90/98
十二、全概率模型
- 定理:
A1、A2……An是个完备事件组
P(B) = ∑P(Ai)P(B|Ai)=P( A1)P(B|A1)+……+P(An)P(B|An)
文字解释:
B事件发生的概率=各情况下发生B的概率之和
.
A1、A2……An不一定得是个完备事件组,只要A1、A2……An包含事件B即可
- 例子:
有四条生产线:第一条生产线生产15%的商品,商品合格率为0.05;第二条生产线生产20%的商品,商品合格率为0.04;第三条生产线生产30%的商品,商品合格率为0.03;第一条生产线生产35%的商品,商品合格率为0.02。
问:
从生产产品抽出一件不合格产品的概率
解:
A1、A2、A3、A4分别为抽一、二、三、四生产线的产品,B为抽出不合格事件
P(B) = P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)+P(A4)P(B|A4) = 0.150.05+0.20.04+…30.03+0.350.02 = 0.0315
十二、贝叶斯公式
- 全概率公式:知道原因推结果。
例子:
因:感冒、肺炎、白血病、自恋
果:发烧
全概率:知道病因,推发烧的概率
- 贝叶斯公式:知道结果推原因
例子:
因:感冒、肺炎、白血病、自恋
果:发烧
贝叶斯:知道结果,推何种原因导致的概率最大
-
例子:
有四条生产线:第一条生产线生产15%的商品,商品合格率为0.05;第二条生产线生产20%的商品,商品合格率为0.04;第三条生产线生产30%的商品,商品合格率为0.03;第一条生产线生产35%的商品,商品合格率为0.02。
问:
从生产产品抽出一件不合格产品,该产品是四号生产线的概率
解:
设A1、A2、A3、A4分别为抽一、二、三、四生产线的产品,B为抽出不合格事件
P(A4B) = P(B)P(A4|B) = P(A4)P(B|A4)
P(A4|B) = P(A4B)/P(B) = {P(A4)P(B|A4)} / P(B) -
定理:
A1、A2……An是个完备事件组,P(Ak|B) = P(Ak)P(B|Ak) / ∑P(Ai)P(B|Ai) = P(AkB)/P(B)
文字解释:
在Ak条件下发生的概率=Ak和B同时发生的概率÷B发生的概率
.
P(Ai)为先验概率—原因的占比,比较好求
P(Ai|B)为后验概率–在结果已知下原因的占比,比较难求
十三、事件的独立性
- 定义:
P(A)>0、P(B)>0
A的概率不受B发生与否的影响,P(A|B) = P(A) - 定理:
P(A)>0、P(B)>0
A、B独立<==>P(AB)=P(A)P(B)
P(A)=0或P(B)=0也成立
所有,有定义:
A、B独立<==>P(AB)=P(A)P(B)
- ∅,Ω与任意事件A都独立
∅与A:
P(∅A) = P(∅) =0
P(∅)P(A)=0
∴∅与A独立
.
Ω与A:
P(ΩA) = P(A)
P(Ω)P(A)=P(A)
∴∅与A独立
- 定理:
(1)若A、B独立,则A与B逆、A逆与B、A逆与B逆独立
(2)若P(A)=0或P(A)=1,则A与任何事件独立 - 独立和互不相容
(1)独立:两个人很陌生,上自习不受彼此的影响
互不相容:有你没我,有我没你,上自习不在一个教室
(2)P(A)>0、P(B)>0时,独立和互不相容不同时成立
A、B独立,P(AB)=P(A)P(B)>0
AB=∅,P(AB)=0、P(A)P(B)>0
- .
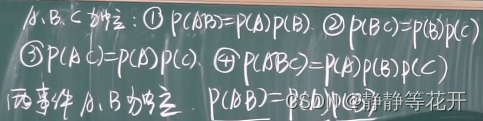
- 例子:
P(A+B) = 0.9,P(A)=0.4,求P(B)
(1)当A、B互不相容
既AB=AB=∅,P(AB)=0
P(A+B) = P(A)+P(B)-P(AB)
0.9 = 0.4 + P(B)-0
P(B)=0.5
(2)A、B独立,P(AB)=P(A)P(B)
P(A+B) = P(A)+P(B)-P(AB)
0.9 = 0.4 +P(B) -0.4P(B)
P(B) = 5/6
十四、伯努利模型
-
概念
(1)独立实验序列:
E1……En这n个实验序列都独立
(2) n重独立实验:
E、E、……E把一个实验做n次,En
(3) 伯努利实验:
结果只有两种,Ω={A,A逆}
(4) n重伯努利实验:
做n次独立实验,且实验结果只有两种 -
定理:
A的概率P(0<P<1),则A逆=1-P,n重伯努利中A发生k次的概率:Pn(k)=CnkPk(1-P)n-k =CnkPkqn-k(q=1-P) 【二项概率公式】 -
例子:
产品废品率为0.1,合格率为0.9,每次取一个放回,取三次。
(1)恰有一次取废品:C310.1*(0.9)2
(2)恰有两次取废品:C32(0.1)20.9
(3)三次取废品:C33(0.1)3
(4)三次取正品:C30*(0.9)3
第二章
一、随机变量的概念
- 例子:
丢骰子:随机变量X可以为1、2、3、4、5、6
丢硬币:随机变量X可以为0、1
灯泡寿命:随机变量X可以为[0,+∞] - 定义:X=X(w)实值函数的值可映射到样本空间Ω
- {w|X(w)=a}事件 <==> {X=a}
该事件发生概率:P{X=a} - 例子:
有一个公交站,每5分钟发一趟,讨论乘客候车时间。
X可为[0,5],P{X≥0}=1,P{X>6}=0 - 离散型:有限个,无限可列个
非离散型:连续性
二、离散型随机变量及其概率分布
- 定义:
X的所有取值Xk(k=1,2……)有限可列个,P{X=Xk}=Pk为其概率函数(分布)。 - 性质:
(1)Pk≥0
(2)∑Pk=1 - 例子:
有5个黑球,3个白球,每抽一个不放回,直到取到黑球,X为取白球的数目。
问:P{-1<X<0},P{1<X<3}、P{X≤3}
解:
X=0,P{X=0}=5/8
X=1,P{X=1}=3/85/7
X=2,P{X=2}=3/82/75/6
X=3,P{X=2}=3/82/71/65/5
P{-1<X<0}=0
P{1<X<3}=P{X=2}
P{X≤3}=P{X=0}+P{X=1}+P{X=2}+P{X=3}
三、连续性随机变量及其概率密度函数
- 例子
统计了99年的降水量,其中降水量在670-770的有1年(频率:0.01),降水量在770-870的有8年(频率:0.081),降水量在870-970的有9年,降水量在970-1070的有19年,降水量在1070-1170的有20年,降水量在1170-1270的有18年,降水量在1270-1370的有10年,降水量在1370-1470的有7年,降水量在1470-1570的有4年,降水量在1570-1670的有3年。
频数直方图:
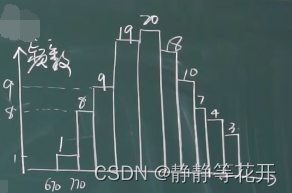
频率密度直方图:(纵坐标为频率/组距)

频率直方图性质:
(1)每个小长方形面积等于该组的频率
(2)所有长方形面积之和为1
(3)介于x=a、x=b之间的面积近似于(a,b]的频率
(4)当组距取得很小,形成一条光滑曲线,该曲线可看作概率密度函数
- 概率密度函数定义:
非负可积f(x),f(x)≥0,P{a<x≤b}=∫abf(x)dx;
【x-连续性随机变量,f(x)-概率分布密度函数】
性质:
(1)f(x)≥0
(2)∫+∞-∞f(x)dx = 1
(3)连续变量取个别值的概率为0。(概率为0的事件2未必是不可能事件)
(4)连续情况下,端点无所谓。P{a≤x≤b}=P{a<x<b}
- 概率密度函数f(x)的值:X取x附近值的大小,既P{x<X<x+Δx}
第一行对上下同时趋于0,用洛必达对Δx求导
四、分布函数
- 分布函数的定义:
F(x) = P(X≤x),既X取值不超过x的概率 - 性质:
(1)0≤F(x)≤1,x∈(-∞,+∞)
(2)F(x)不减,x1<x2,F(x1)≤F(x2)
(3)
(4)

(5)F(x) = P{X≤x}
P{X≤a} = F(a)
P{X>a} = 1-P{X≤a} = 1-F(a)
P{a<X≤b} = P{X≤b}-P{X≤a}=F(b)-F(a)
五、离散型的分布函数
- 例子:
| X | -1 | 2 | 3 |
|---|---|---|---|
| P | 1/2 | 1/3 | 1/6 |
问:
求概率分布函数
解:
x<-1,F(x) = P(X≤x)=0
-1≤x<2,F(x) = P(X≤x)=P(X=-1)=1/2
2≤x<3,F(x) = P(X≤x)=P(X=-1)+P(X=2)=5/6
3≤x,F(x) = P(X≤x)=P(X=-1)+P(X=2)+P(X=3)=1
画图时,实心点在线段的左端。
- 分布函数求概率密度函数:
间断点xk是X的取值
P(X=xk) = F(xk) - F(xk-0),既F(xk)减去朝左偏一点点的值
六、连续型的分布函数
-
F(x) = P{X≤x}=∫x-∞f(t)dt,该F(x)是连续的,F’(x)=f(x)
-
例子:
 问:
问:
已知道概率密度函数,求分布函数
解:
x<0时,F(x) = ∫x-∞0dt=0
0≤x<2时,F(x) = ∫x-∞ f(t)dt=∫0-∞ 0dt+∫x-∞ (-1/2t+1)dt = -1/4x2+x
2≤x时,F(x) = ∫x-∞ f(t)dt=∫0-∞ 0dt+∫2-0 (-1/2t+1)dt+∫x2 0dt = 1
七、0-1分布
- 只有两种结果,且只做一次
| X | 0 | 1 |
|---|---|---|
| P | p | 1-p |
- P{X=k} = pk(1-p)1-k,k=0,1
六、几何分布
- P(A)=p;第k次首次发生,前k-1次没发生:P{X=k}=(1-p)k-1p
- 例子:
射中目标的概率为0.6,X:直到射中目标的次数
P{x=k}=0.4k-1*0.6
七、二项分布(X~B(n,p))
- P(A)=p;n次实验发生了k次:P{X=k}=Cnkpk(1-p)n-k,k=0,1,2……n
- 最可能值:
(1)(n+1)*p不为整数,[(n+1)*p] (取整)达到最大值
(1)(n+1)*p为整数,(n+1)*p和(n+1)*p-1都是最大值 - 例子:
存在报警器,当发生危险时报警器报警的概率是0.8;若要保证发生危险时99%的可能报警。需要安装多少台报警器。
解:
X:发生危险时报警的台数,n:安装台数。X~B(n,p)
既求0.99≤P{X≥1}=1-P{X=0}=1-C0n0.2n
八、泊松分布(X~P(λ))
-
可用于近似二项分布
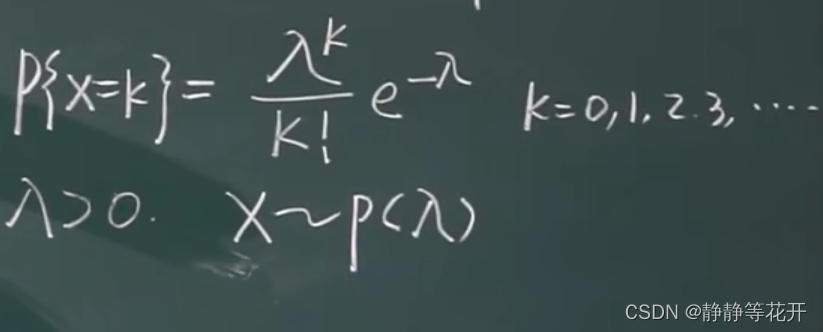
-
泊松分布表
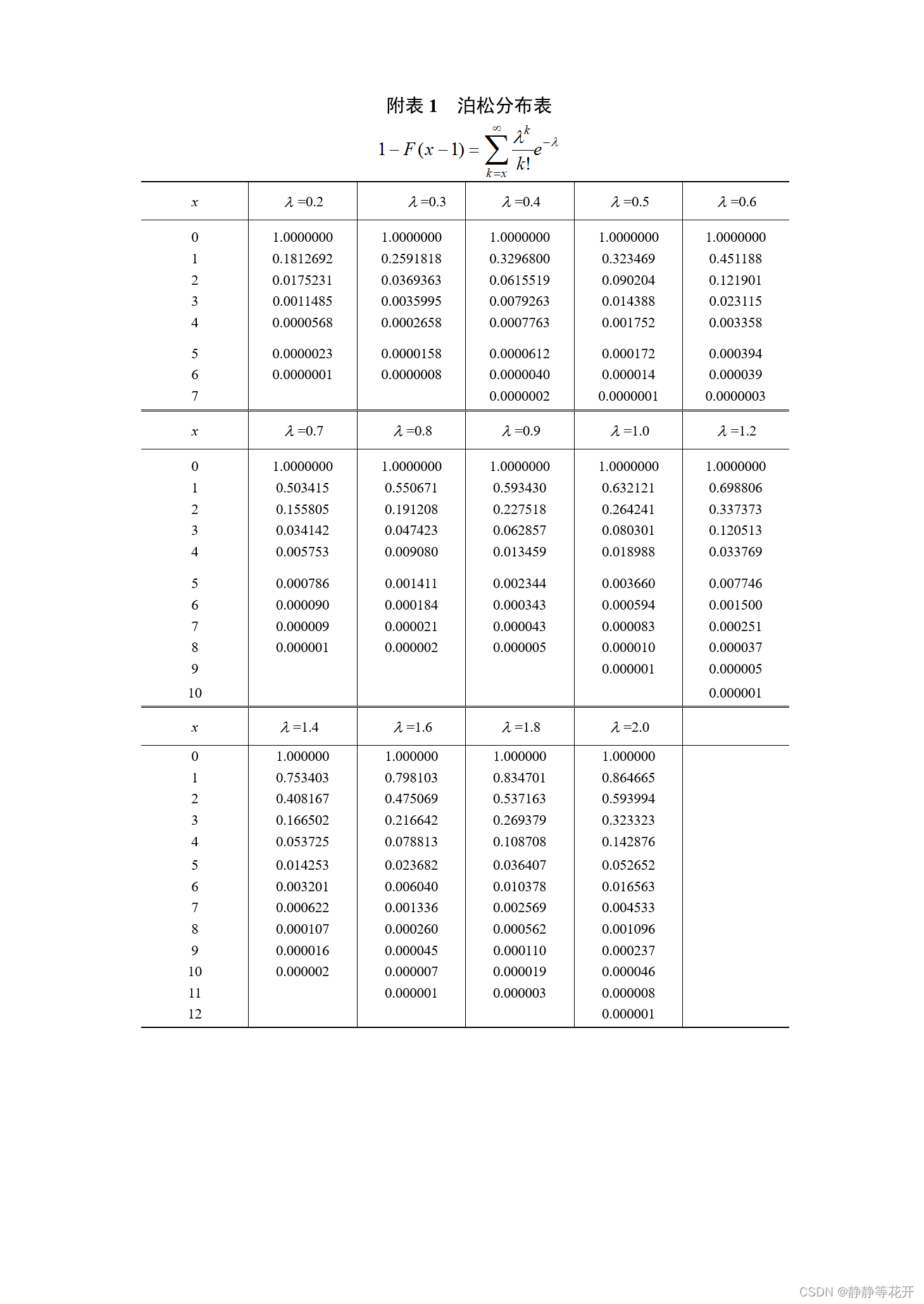
-
当二项分布的n比较大、p比较小、np适中(n≥100,np≤10),可用泊松分布来近似计算(λ=np)
-
例子:
电话台用户呼叫次数X~P(3),λ=3。
问:用户呼叫不超过5次的概率
解:
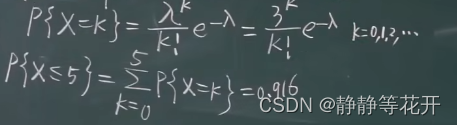
-
例子:
证券部有1000个账户,每户10万元,每户提20%的概率是0.006。
问:准备多少现金95%以上的概率能满足用户
解:
X:提钱的用户数 X~B(1000,0.006)满足二项分布
准备现金x元,既求P{2万元*X≤x}≥0.95–>P{X≤x/2}≥0.95
可用泊松分布近似:

得出x/2≥10
九、超几何分布
-
N个元素:N1个属于第一类,N2个属于第二类;取n个,X:n个属于第一类的个数
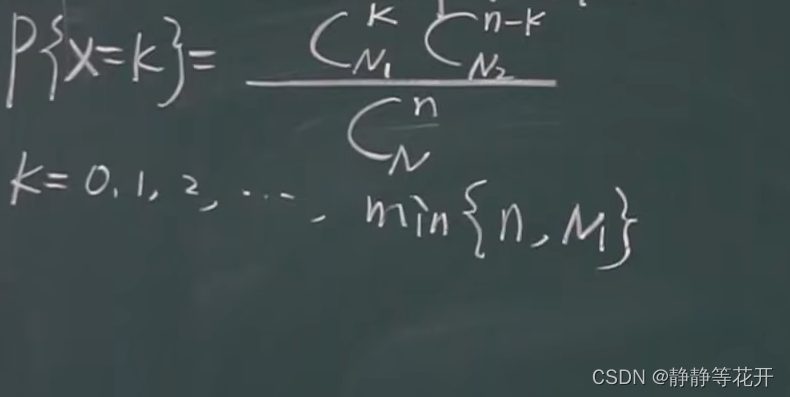
-
例子:
20名(5女、15男),任取4名;X:4名中女生的人数

-
超几何分布可以用来描述不放回抽样实验
N很大时,n相对于N很小,p改变会很小
例子:
有10000粒种子,发芽率99%;取200粒,问至多一粒不发芽的概率。
【抽种子会影响到发芽率p,但是200相对10000很小,可用超几何分布来描述】
解:
10000*1% = 100粒----不发芽
所以:N1:9900 N2:200 n=200
计算很麻烦,所以我们用二项分布来近似
计算仍然很麻烦
可以进一步用泊松分布来近似
- 总结:
二项分布:n≥100,np≤10时,用泊松分布近似。
超几何分布N很大,n/N很小时,可以用二项分布来近似,再进一步用泊松分布近似
十、均匀分布(X~U[a,b])
-
定义:

概率函数图:
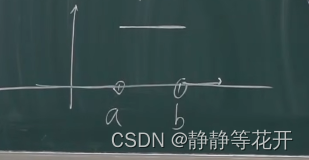
-
分布函数
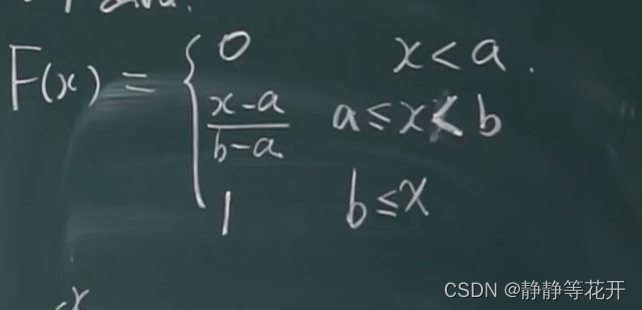
-
某区间的概率=某区间长度/总区间长度

-
例子:

解:
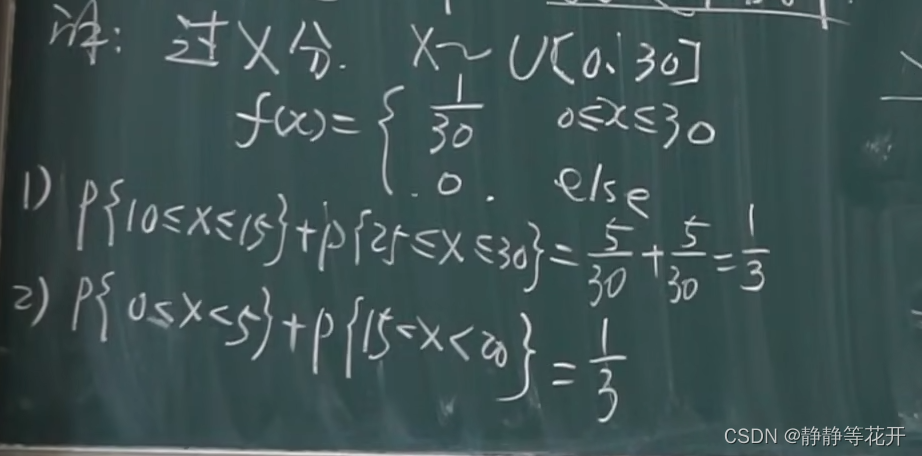
十一、指数分布
-
概率密度函数
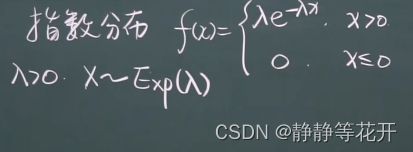
-
分布函数:

-
例子:
灯泡的使用寿命为X,其概率密度函数为:

灯泡有三个元件,各元件都未损坏时的才可正常工作。
问:
求灯泡工作大于1000小时的概率
解:

(1)指数分布没有记忆性,既灯泡的使用寿命与当地寿命无联系。
(2)X~指数分布,s>0,t>0;P{X>s+t|X>s}=P{X>t}
十二、正态分布
-
概率密度函数
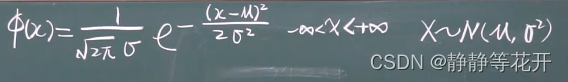
-
分布函数(积不出来)

-
性质:
(1)y=Φ(x)以x=u为对称轴
(2)x=u时,Φ(x)取到最大值
(3)y=Φ(x)以x轴为渐近线,x±σ为拐点
(4)σ固定,u变化,图像左右移动;u固定,σ变小,最高点上移,σ变大,最高点下移 -
标准正态分布:u=0,σ=1
概率密度函数:

性质:
(1)y轴是对称轴,为偶函数
(2)概率密度函数:Φ0(x)=Φ0(-x)
(3)分布函数:Φ0(-x)=1-Φ0(x)
- 正态分布的标准化:
概率密度函数:

分布函数:

- 例子:X~N(1,4),u=1,σ2=4。
问:
P{0<X<1.6}=?
解:
X非标准正态分布,先转换成标准正态分布
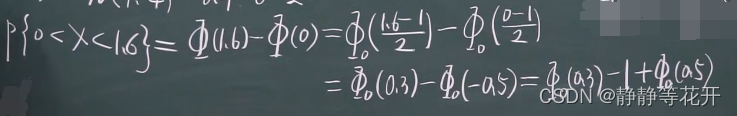
- X~N(0,1),给定a(0<a<1),找U a,使P{X>Ua}。(Ua叫上a分位数)
例子:
对于U0.05,P{X>1.645}=0.05,所以U0.05=1.645。
0.05–>x=1.645右侧阴影部分面积
十三、随机变量函数的分布(离散型)
-
探讨问题类型:已知X是某分布,Y=aX+b是什么分布?
-
例子:
| X | -1 | 0 | 1 | 2 |
|---|---|---|---|---|
| P | 0.1 | 0.3 | 0.4 | 0.2 |
对于Y=4X
| X | -4 | 0 | 4 | 8 |
|---|---|---|---|---|
| P | 0.1 | 0.3 | 0.4 | 0.2 |
对于Z=X2
| X | 1 | 0 | 4 |
|---|---|---|---|
| P | 0.5 | 0.3 | 0.2 |
对于重复的1要进行合并
十四、随机变量函数的分布(连续型)
- 讨论问题类型:
设X的概率密度函数为fx(x);构造新的变量y = g(x);Y=g(x),问Y的概率密度函数
(1)将Y的分布函数变为X的分布函数:FY(x)–>FX(x)
(2)FY(x)–>FX(x)左右求导得到概率密度函数:fY(x)<–fX(x)
FY(x) = P{Y≤x}
FX(x) = P{X≤x}
- 例子:
X的密度函数fx(x),Y=3x+2
(1)FY(x) = P{Y≤x} = P{3X+2≤x} = P{X≤(x-2)/3} = FX((x-2)/3)
(2)对FY(x)=FX((x-2)/3)求导, fY(x) = 1/3*fX((x-2)/3) - 若X服从[a,b]均匀分布,Y=kx+c(k≠0)服从相应区间上的均匀分布
- X~N(u,σ),进行Y=(X-u)/σ的线性变化,转换为N(0,1)
- 定理
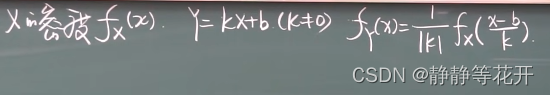
第三章
一、二维随机变量及其分布函数
-
假设E是随机试验,Ω是样本空间,X、Y是Ω的两个变量;(X,Y)向量就叫做二维随机变量。
X、Y来自同一个样本空间 -
分布函数:
,称为X、Y的联合分布
取左下方部分

-
性质:
(1)0≤F(x,y) ≤1
(2)F(x,y) 不减:y固定,x1<x2,F(x1,y)<F(x2,y)
(3)F(-∞,y)=F(x,-∞)=F(-∞,-∞)=0,
F(+∞,+∞)=1
(4)F(x,y)关于x和y右连续
(5)x1<x2,y1<y2,P{x1<X≤x2,y1<Y≤y2} = F(x2,y2) - F(x2,y1)-F(x1,y2)+F(x1,y1) -
X的边缘分布:FX(x) = P{X≤x} = F(x,+∞) = P{X≤x,Y<+∞}
Y的边缘分布:FY(y) = P{Y≤y} = F(+∞,y) = P{X<+∞,Y≤y}
二、二维连续型的联合分布与边缘分布
- X、Y取离散值
例子:
分布表:
性质:
-
分布函数:
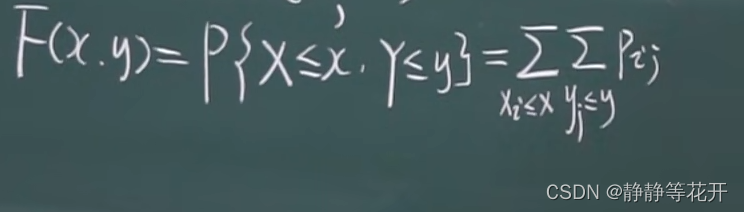
-
边缘分布
| X\Y | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 0 | 1/2 | 1/8 |
| 2 | 1/8 | 1/8 | 1/8 |
X的边缘分布:(不看Y)
| X | 1 | 2 |
|---|---|---|
| P | 5/6 | 3/8 |
Y的边缘分布:(不看X)
| Y | 1 | 2 | 3 |
|---|---|---|---|
| P | 1/8 | 5/8 | 1/4 |
(1)联合分布可唯一确定边缘分布
(2)边缘分布不能确定联合分布(X、Y独立除外)
- F(x,y) = P{X≤x,Y≤y} = ∫x-∞∫y-∞f(s,t)dsdt
F(x,y)是分布函数,f(s,t)是联合密度
f(s,t)性质:
概率密度函数的体积,为对应的概率分布函数值
三、二维连续型随机变量的边缘密度函数
- Fx(x) = F(x,+∞) = ∫x+∞[∫-∞+∞f(s,t)dt]ds
Fx`(x) = fx(x)=∫-∞+∞f(x,t)dt=∫-∞+∞f(x,y)dy - (1)二维正太分布的边缘分布也是正态分布
(2)两个边缘分布是整体分布,其二维分布并非是正太分布
四、条件分布的定义
- 在一个事件A的发生之下的分布:F(x|A) = P{X≤x|A}
- 例子:
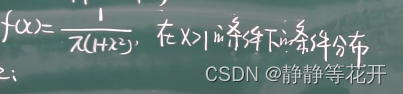
解:
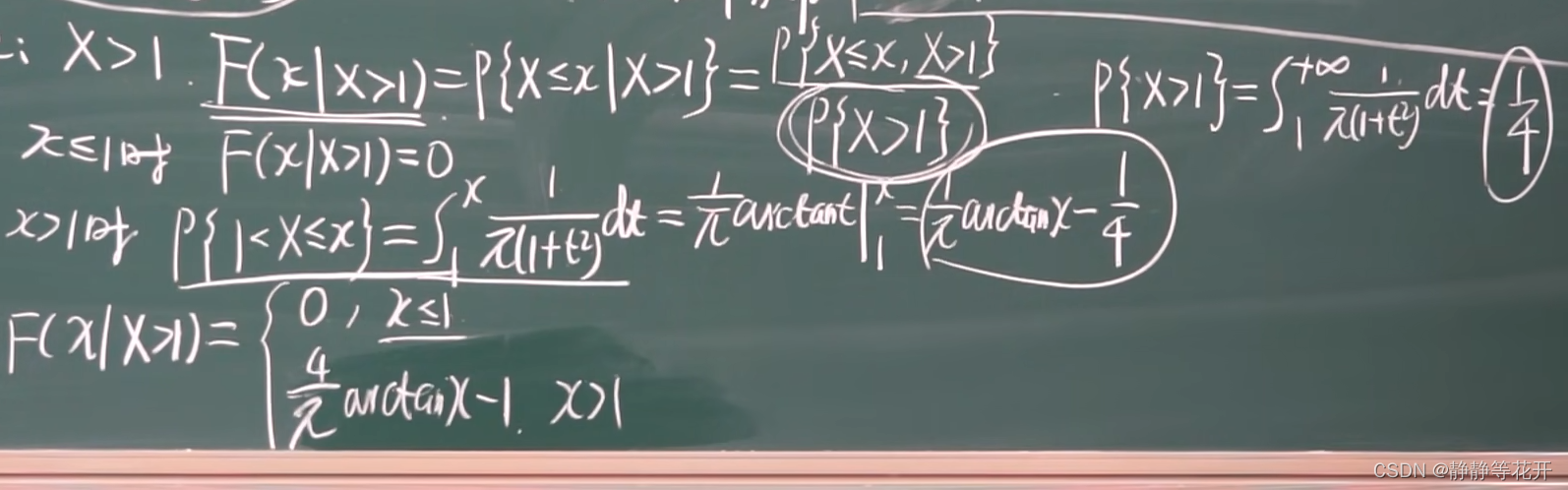
五、离散型随机变量的条件分布
- 例子
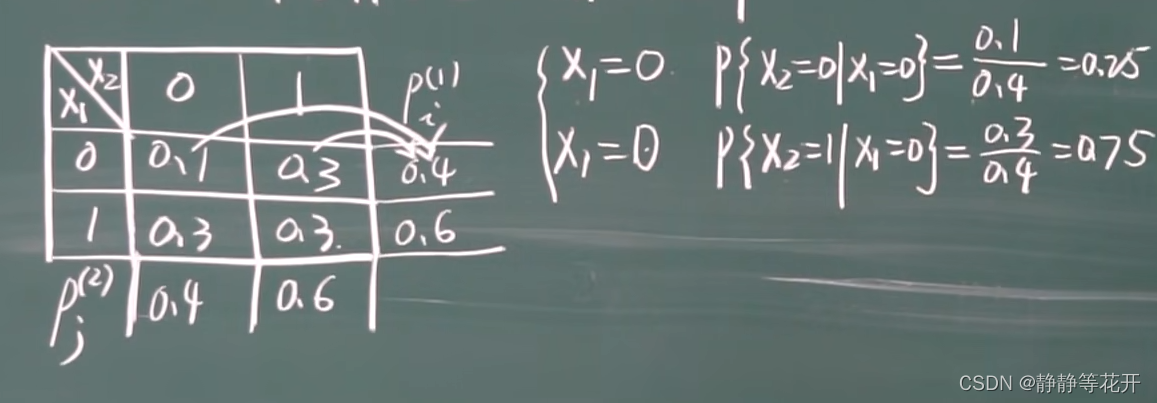
六、连续型随机变量的条件分布
- 定义:(X,Y)-二维随机变量,f(x,y)-概率密度函数,fX(x)、fY(y)-边缘密度函数。若fY(y)>0,在Y=y的条件下,F(x|y) = ∫x-∞f(u,y)/fY(y)du,f(x|y) = f(x,y)/fY(y)
- P{X≤x|Y≤y} = P{X≤x,Y≤y}/P{Y=y},若P{Y=y}=0如何解决?
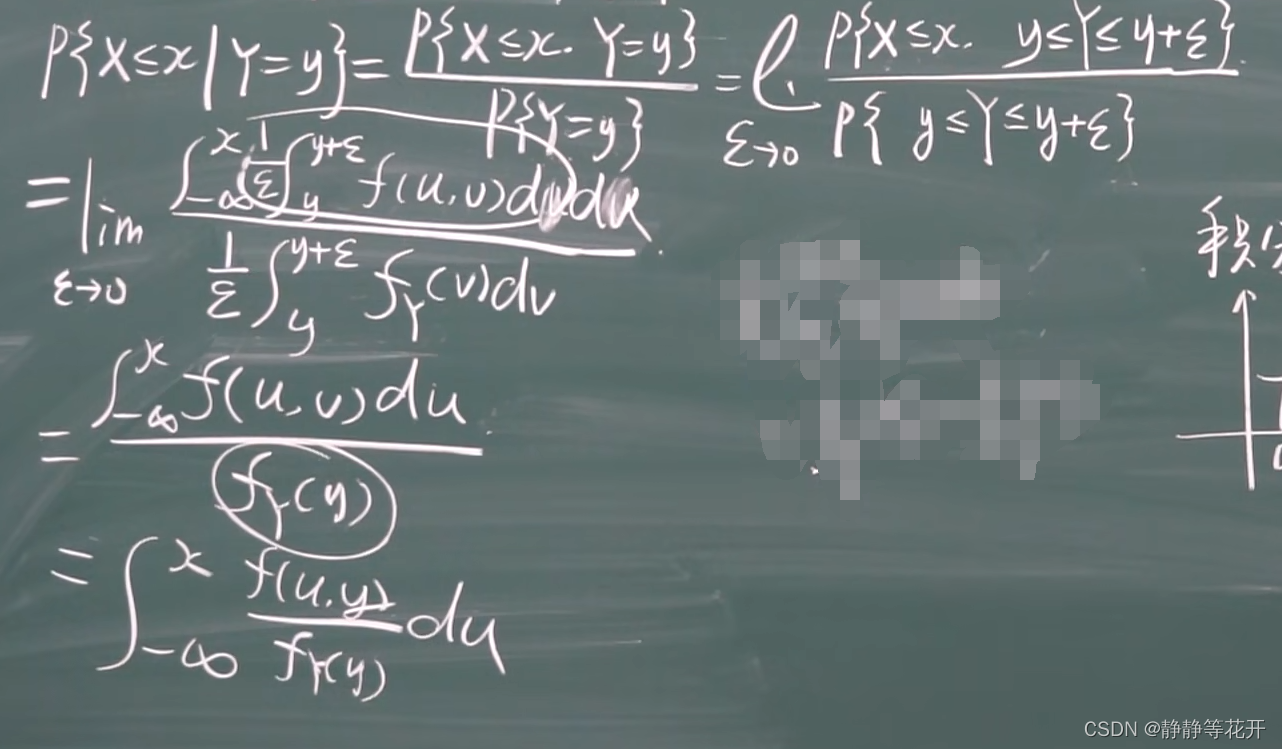
第二到第三行用到积分中值定理
七、随机变量的独立性
- f(x|y) = fx(x) = f(x,y)/fY(y),所以:
随机变量相互独立= =>
(1)f(x,y)=fX(x) *fY(y)
(2)F(x,y)=FX(x) *FY(y)
随机变量相互独立<= =>P{X∈Sx,Y∈Sy}=P{X∈Sx}*P{Y∈Sy} - 例子:
经理会在8-12点到办公室,秘书会在7-9小时到办公室,他们到办公室的时间是独立的。
问:
他们到办公室时间不超过5分钟(1/12小时)的概率
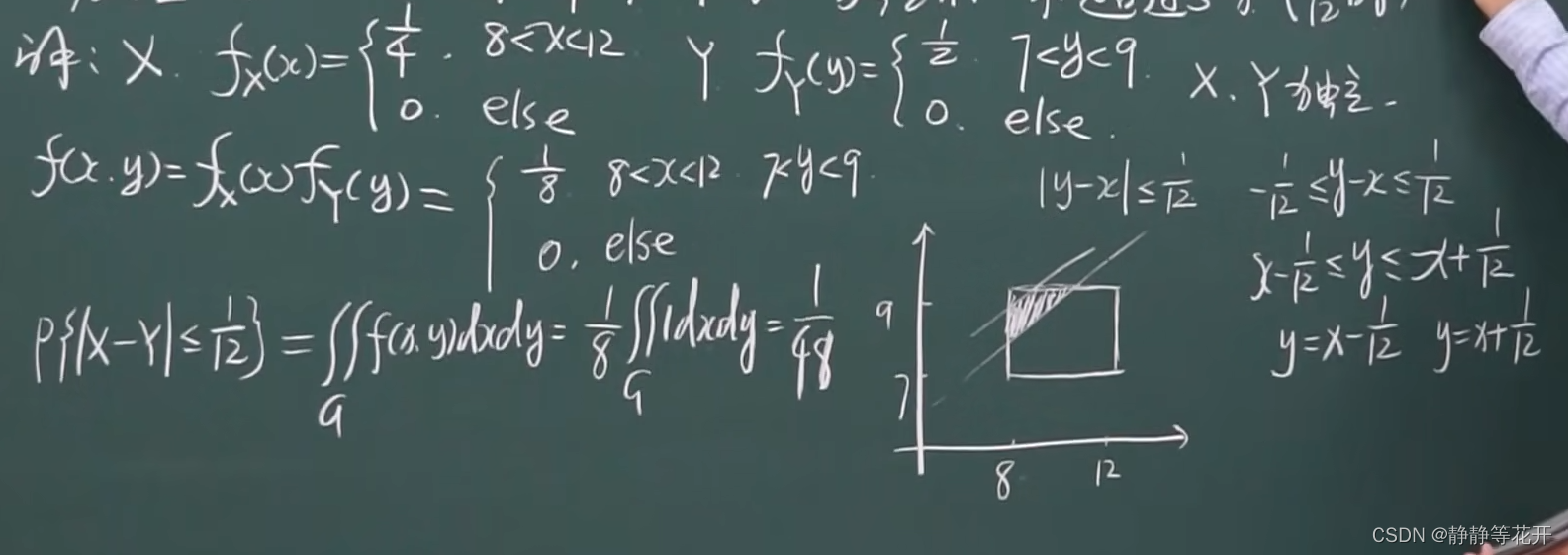
- 定理:
X、Y独立,g1(x)和g2(x)也独立
八、二维离散型随机变量函数的分布
- 例子:
设测量某物的长、宽分别为:X、Y
| X\Y | 4 | 4.2 |
|---|---|---|
| 5 | 0.2 | 0.4 |
| 5.1 | 0.3 | 0.1 |
则面积的Z=XY
| Z | 20 | 21 | 20.4 | 21.4 |
|---|---|---|---|---|
| P | 0.2 | 0.4 | 0.3 | 0.1 |
九、二维连续型随机变量函数的分布
- 存在随机变量X、Y,概率密度函数f(x,y);现构造一个新的随机变量Z=g(x,y),求Z的的分布。
(1)FZ(z) = P{Z≤z} = P{g(x,y)≤z}=∫∫Dzf(x,y)dxdy,Dz = {(x,y)|g(x,y)≤z}
(2)FZ(z) = ∫∫Dzf(x,y)dxdy左右求导,F`Z(z)=fZ(z) - 扩展
- 卷积公式:
对于随机变量X、Y,相互独立,Z=X+Y
则:
(1)fZ(z) = ∫+∞-∞f(x,z-x)dx = ∫+∞-∞fX(x)fY(z-x)dx
(2)fZ(z) = ∫+∞-∞f(z-y,y)dy = ∫+∞-∞fX(z-y)fY(y)dy- 两个正态分布相加
X~ N(u1,σ12),Y ~N(u 2,σ22),X+Y~N(u 1+u2,σ12+σ22)
第四章
一、离散型变量的数学期望
- 3位评委打分,专业评委打90分,普通评委打80分,最次的评委打60分。
(1)平均数:(90+80+60)/3
(2)加权平均数:专业评委打分占比90%,普通占9%,最次占1%,90* 0.9+80* 0.09+60*0.01 - 离散型的期望
P(X=xk)=Pk,若∑xk*Pk (k=1~ ∞)收敛,则EX=∑xk*Pk (k=1~ ∞) - 例子
甲、乙每天各生产的产品数x1、x2件次品数,
| X1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.3 | 0.3 | 0.2 | 0.2 |
| X2 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| P | 0.2 | 0.5 | 0.3 | 0 |
问:谁的技术水平高?
解:
EX1=0x0.3+1x0.3+2x0.2+3x0.2=1.3
EX2=0x0.2+1x0.5+2x0.3+3x0=1.1
甲牛一些
二、连续型变量的数学期望
- 变量X,概率密度函数f(x),∫+∞-∞xf(x)dx绝对收敛,EX = ∫+∞-∞xf(x)dx
∫+∞-∞xf(x)dx—x看作取值,f(x)看作概率
- 例子:
某灯泡先用后付款,灯泡寿命符合λ=1/10的泊松分布;设寿命为X,X≤1年,付费1500;1<X≤2年,付费2000;2<X≤3年,付费2500;3<X≤4年,付费3000。

三、随机变量函数的数学期望
- 存在变量X和Y,Y=g(x),
(1)(离散)X数学期望为∑xiPi,Y数学期望为∑g(xi)Pi
(2)(连续)X数学期望为∫+∞-∞xf(x)dx,Y数学期望为∫+∞-∞g(x)f(x)dx - 二位变量函数
存在二维变量(X,Y),求Z=g(X,Y)的期望
(1)离散:
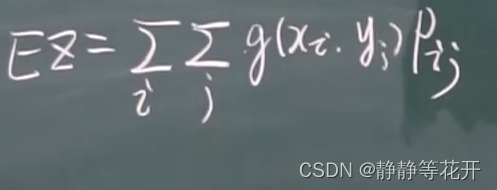
例子:
(2)连续:
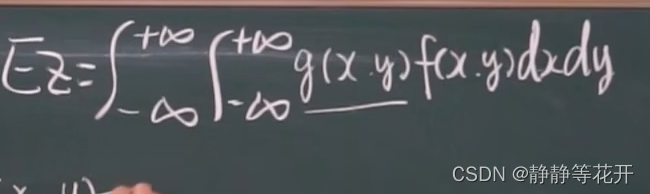
四、数学期望的性质
- 常数的期望等于常数,EC=C
- E(X+C)=EX+C
- E(CX)=C*EX
- E(kX+b)=k*EX+b
- E(X±Y)=EX+EY (任何时候都成立 )
E(∑CiXi) = ∑CiEXi - X、Y独立,E(XY)=EX*EY
五、条件期望
- 定义:
一个变量取某值,另一个变量的期望 - (离散)
E(X|Y=yi) = ∑xiPi(X=xi|Y=yi)
E(Y|X=xi) = ∑yiPi(Y=yi|X=xi)
例子:
问:E(Y|X=1)?
解:
(1)先求Y的条件概率
(2)E(Y|X=1) = 1* 0.5+2* 0.25+3* 0.25
- (连续)
E(X|Y=y) = ∫-∞+∞xf(x|y)dx
E(Y|X=x) = ∫-∞+∞yf(y|x)dy
六、方差的定义
- 方差:DX = E(X-EX)2,表示数据偏离EX的程度。标准差:(DX)1/2
- (离散)DX = ∑(xk-EX)2Pk
(连续)DX = ∫-∞+∞(x-EX)2f(x)dx - DX =E(X-EX)2=E(X2-2XEX+(EX)2)= EX2-2(EX)2+(EX)2=E(X2)-(EX)2
既DX=E(X2)-(EX)2
七、方差的性质
- 常数的方差DC = 0
- D(X+C) = DX
- D(CX) = C2DX
- D(kX+b) = k2DX
- X、Y独立,D(X±Y) = DX+DY
推论:D(x1+x2+……+xn)=D(x1)+D(x2)+……+D(xn)
- DX = 0<==>P(X = EX) = 1
- 方差与期望对比:
- x按以下处理就会1变成期望=0,方差=1
称为标准化
八、常见离散型的期望与方差
- 0-1分布:
| X | 0 | 1 |
|---|---|---|
| p | 1-p | p |
EX=p,DX = EX2-(EX)2=p-p2=pq
-
二项分布:
P(x=k) = Cknpkqn-k,k=0,1,……n
EX = np
DX = npq -
几何分布:
P(x=k) = (1-p)k-1p,k=1,2,……
EX = ∑k(1-p)k-1p = (∑k(1-p)k-1)p = (1/p2)*p = 1/p
DX = (1-p)/p2
扩:
- 泊松分布:

EX = λ
DX=λ2+λ
九、常见连续型的期望与方差
-
均匀分布

EX = ∫abx(1/b-a)dx = (a+b)/2
DX = (b-a)2/12 -
指数分布:
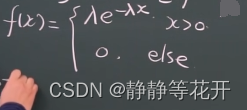
EX = 1/λ
DX = 1/λ2 -
正态分布:
X~N(u,σ2)
EX = u
DX = σ2
总结:
十、协方差
-
定义:
Cov(x,y) = E[(X-EX)(Y-EY)] = E(XY) -EXEY -
D(X±Y) = DX+DY±2Cov(x,y)
-
例子:

求Cov(x,y)并判断是否独立。
解:
(1)边缘分布

EX = 0,EY = 0,E(XY)=1/8-1/8-1/8+1/8=0
Cov(x,y) = 0-0,(3/8)*(3/8)!=1/8所以不独立 -
例子:

解:
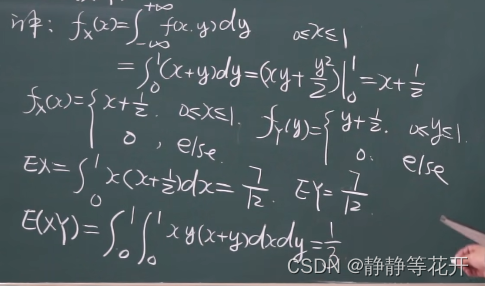
Cov(x,y) = E(XY)-EXEY = -1/144 -
cov性质:
(1)Cov(X,Y) = Cov(Y,X)
(2)Cov(aX,bY) = abCov(X,Y)
(3)Cov(X1+X2,Y) = Cov(X1,Y)+Cov(X2,Y)
(4)Cov(C,X) = 0
(5)X、Y独立,Cov(X,Y) = 0 -
Cov(X,Y)衡量X、Y的关系,受计量单位的影响进行标准化可避免该影响。
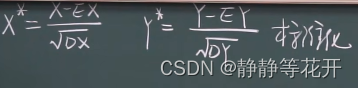
标准化后:EX = Cov(X,Y)/[(DX)1/2(DY)1/2]=ρ
cov(X,Y)>0,表明X与Y正相关
cov(X,Y)=0,表明X与Y无关
cov(X,Y)<0,表明X与Y负相关
十一、相关系数
-
(线性)相关系数:
ρ=Cov(X,Y)/[(DX)1/2(DY)1/2] = [E(XY)-EXEY]/[(DX)1/2(DY)1/2]
ρ与Cov(x,y)同正、同负、同0 -
|ρ|≤1
引理:[E(XY)]2≤EX2EY2 -
定理:
|ρ|=1<==>X与Y间以ρ=1成线性关系,既 P(Y=aX+b)=1
(1)ρ=1,X、Y完全正相关
(2)ρ=-1,X、Y完全负相关
(3)|ρ|接近0,X、Y线性关系很弱
(4)ρ=0,X、Y不存在线性关系
- X、Y不相关与X、Y独立:
X、Y不相关:X与Y不存在线性关系
X、Y独立:X、Y不存在任何关系(包括线性、非线性关系)
(1)独立一定不想关,不相关不一定独立
(2)独立<==>f(x,y) = fX(x)fY(y)
(3)二维正态分布,独立与不相关是等价的
十二、中心矩与原点矩
- 原点矩:Exk,以原点为中心(E(x-0)k)
期望:EX,也称一阶原点矩
原点矩:
(1)离散:∑xikPi
(2)连续:∫+∞-∞xkf(x)dx
- 中心距:E(X-EX)k,以EX为中心
一阶中心距:E(X-EX) = EX-EX=0
二阶中心矩:E(X-EX)2 为方差
中心矩:
(1)离散:∑(xi-EX)kPi
(2)连续:∫+∞-∞(x-EX)kf(x)dx








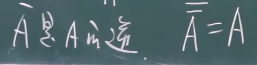
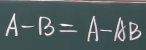
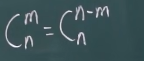
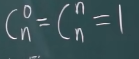
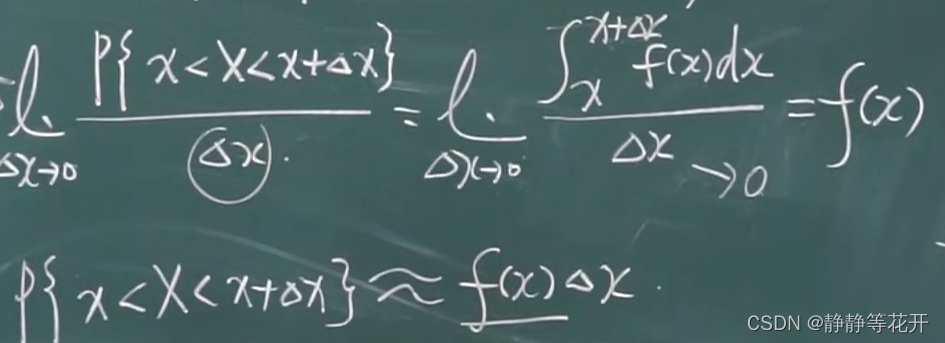
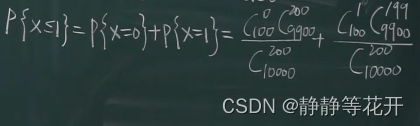


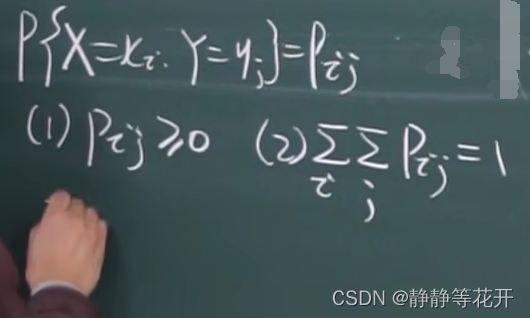
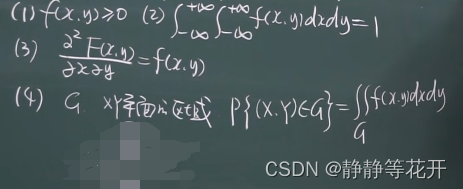
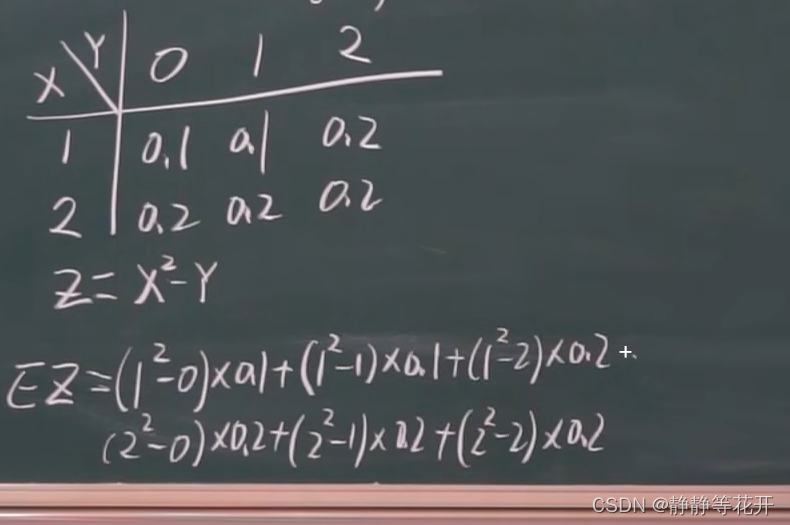



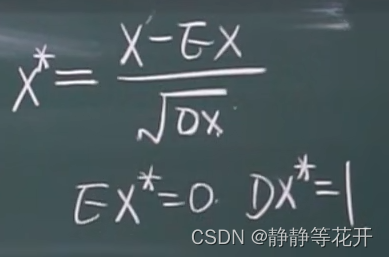















 1416
1416











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








