盲均衡 CMA、MCMA、SEI与MSEI

量大龙神魔

已于 2023-05-29 10:51:50 修改

阅读量6.5k

点赞数 20

文章标签：算法矩阵信号处理信息与通信

于 2023-05-28 16:37:23 首次发布

本文链接：https://blog.csdn.net/qq_45471796/article/details/130907275

版权

最近由于某些原因接触到了这一方面，在此做一个简单的记录。

高速无线通信中，由于信道衰落、多径传播等的影响，在接收端会产生严重的码间干扰，增加了系统的误码率。为了克服码间干扰，提高系统的性能，在接收端需采用均衡技术。目前主要采用基于训练序列的自适应均衡技术或不使用训练序列的盲均衡技术。盲均衡相对于自适应均衡，不需要训练序列，但是需要信号的先验统计信息，因此该种方法在协作通信场景下应用的较为多。

CMA

CMA算法全称恒模盲均衡算法(Constant Modulus Algorithm)，是该领域较为经典的一个算法，即使在有相位误差的情况下也能收敛，因此它已得到了广泛的应用，但是算法收敛速度较慢，而且由于其代价函数不包含相位信息，相位误差得不到补偿，所以在均衡之后还需经过相位恢复来消除相位误差的影响。该算法于1980年由Godard在TComm上提出，其特点是利用隐含的高阶统计特性构造代价函数，通过调节均衡器的权向量寻找代价函数的极值点，其思想与LMS算法类似，其结构如下图所示：

图中 $a(n)$ 是零均值独立同分布的发射信号； $c(n)$ 是信道脉冲响应； $w(n)$ 为加性高斯白噪声； $y(n)$ 为均衡器接收信号； $f(n)$ 为均衡器权向量； $z(n)$ 为均衡器输出信号； $\hat {a} (n)$ 为后续的判决装置对 $z(n)$ 的判决输出信号。CMA误差函数为：

$e^2\left(n\right)=|z\left(n\right)|^2-R^2=|z\left(n\right)|^2-\frac{\mathrm{E}\{|a(n)|^4\}}{\mathrm{E}\{|a(n)|^2\}}$

其代价函数为：

$J=\operatorname{E}[e^2(n)]\text{=}\operatorname{E}\{[|z(n)|^2-R^2]^2\}$

因此权向量迭代式为：

$\begin{aligned}f(n+1)&=f(n)-\mu(\left|z(n)\right|^2-R^2)y^*(n)z(n) =f(n)-\mu e^2(n)z(n)y^*(n)\end{aligned}$

MCMA

MCMA算法全称修正恒模盲均衡算法(Modified Constant Modulus Algorithm)，是在CMA算法的基础上，通过对接收信号的实部及虚部分开进行处理，一定程度上解决了CMA算法相位误差大的问题，但实际上该算法仍然具有较慢的收敛速度及较大的稳态误差。其代价函数为：

$J(k)=J_R(k)+jJ_I(k)$

$J_R=\operatorname{E}[e_R^2(n)]=\operatorname{E}\{[|z_R(n)|^2-R_R^2]^2\}=\operatorname{E}\{[|z_R(n)|^2-\frac{\mathrm{E}\{|a_R(n)|^4\}}{\mathrm{E}\{|a_R(n)|^2\}}]^2\}$

$J_I=\operatorname{E}[e_I^2(n)]=\operatorname{E}\{[|z_I(n)|^2-R_I^2]^2\}=\operatorname{E}\{[|z_I(n)|^2-\frac{\mathrm{E}\{|a_I(n)|^4\}}{\mathrm{E}\{|a_I(n)|^2\}}]^2\}$

权向量迭代式同CMA算法。

SEI

SEI算法全称超指数迭代算法(Super-exponential Iterative)，该算法于1993年由O. Shalvi与E. Weinstein在TIT上提出，该算法与RLS算法有一定的相似度，通过Q矩阵对接收信号进行预白化，从而使得该算法收敛速度与稳态误差较恒模类算法均有显著改善，其缺点便是计算量相较于CMA算法偏大。该算法误差函数与CMA算法相同，为：

$e^2\left(k\right)=|z\left(k\right)|^2-R^2=|z\left(k\right)|^2-\frac{\mathrm{E}\{|a(k)|^4\}}{\mathrm{E}\{|a(k)|^2\}}$

代价函数为：

$J=\operatorname{E}[e^2(n)]\text{=}\operatorname{E}\{[|z(n)|^2-R^2]^2\}$

权向量迭代式为：

${f}(k+1)={f}(k)+\mu_1{Q}(k){X}^*(k)e(k)$

Q矩阵迭代式为：

${Q}(k+1)=\frac{1}{1-\mu}\left[{Q}(k)-\frac{\mu{Q}(k){X}^*(k){X}^{\text{T}}(k){Q}(k)}{1-\mu+\mu{X}^{\text{T}}(k){Q}(k){X}^{*}(k)}\right]$

Q矩阵初始值为自相关矩阵的逆。

MSEI

MSEI是基于MCMA与SEI而来，对接收信号的实部及虚部分开进行处理。最后通过SEI算法进行处理。处理方法可参考SEI与MCMA。

仿真条件

数据长度	60000
信噪比	15
滤波器长度	17
迭代步长	0.0001(CMA)，0.0004(MCMA)，0.0004(MSEI)
基带调制类型	16QAM
多径信道冲激响应	[0.26-1i0.1, 0.93-1i0.2, 0.26]

代码

CMA

L = 60000;
SNR = 15;
h = [0.26-1i*0.1, 0.93-1i*0.2, 0.26];
h = h/norm(h);
Nf = 17;

M = 16;
sa = round(rand(L,1)*(M-1));
sn1 = qammod(sa',M);

rn = filter(h,1,sn1);
xn = awgn(rn,SNR,'measured');
sn = xn;

R = mean(abs(sn).^4)/mean(abs(sn).^2);

%% CMA（相位偏移严重）
W_cma = zeros(Nf,1);
W_cma((Nf+1)/2) = 1;
muCMA = 0.0001;
for ik = 1:L-Nf
    X_cma(:,ik) = fliplr(xn(ik:ik+Nf-1));
    Y_cma(ik) = W_cma'*X_cma(:,ik);
    E_cma(ik) = (abs(Y_cma(ik))^2-R);
    W_cma = W_cma - muCMA*conj(E_cma(ik))*conj(Y_cma(:,ik))*(X_cma(:,ik));%%存疑  
end
figure();plot(sn(30000-Nf+1:end),'.');title('均衡前');
figure();plot(Y_cma(30000:end),'.');title('CMA算法');

MCMA

L = 60000;
SNR = 15;
h = [0.26-1i*0.1, 0.93-1i*0.2, 0.26];
h = h/norm(h);
Nf = 17;

M = 16;
sa = round(rand(L,1)*(M-1));
sn1 = qammod(sa',M);

rn = filter(h,1,sn1);
xn = awgn(rn,SNR,'measured');
sn = xn;

R = mean(abs(sn).^4)/mean(abs(sn).^2);
Ri = mean(imag(sn).^4)/mean(imag(sn).^2);
Rr = mean(real(sn).^4)/mean(real(sn).^2);
R = mean(abs(sn).^4)/mean(abs(sn).^2);
Ri = Ri/sqrt(Ri^2+Rr^2);
Rr = Rr/sqrt(Ri^2+Rr^2);

%% MCMA
W_mcma = zeros(Nf,1);
W_mcma((Nf+1)/2) = 1;

muMCMA  = 0.0004;
for ik = 1:L-Nf
    X_mcma(:,ik) = fliplr(xn(ik:ik+Nf-1));
    Y_mcma(ik) = W_mcma'*X_mcma(:,ik);
    Yr = real(Y_mcma(ik));
    Yi = imag(Y_mcma(ik));        
    Er_mcma = Yr*(Yr^2-Rr);
    Ei_mcma = Yi*(Yi^2-Ri);
    E_mcma(ik) = Er_mcma+1i*Ei_mcma;
    W_mcma = W_mcma - muMCMA*conj(E_mcma(ik))*X_mcma(:,ik);%%存疑       
end
figure();plot(sn(30000-Nf+1:end),'.');title('均衡前');
figure();plot(Y_mcma(30000:end),'.');title('MCMA算法');

MSEI

L = 60000;
SNR = 15;
h = [0.26-1i*0.1, 0.93-1i*0.2, 0.26];
h = h/norm(h);
Nf = 17;

M = 16;
sa = round(rand(L,1)*(M-1));
sn1 = qammod(sa',M);

rn = filter(h,1,sn1);
xn = awgn(rn,SNR,'measured');
sn = xn;

Ri = mean(imag(sn).^4)/mean(imag(sn).^2);
Rr = mean(real(sn).^4)/mean(real(sn).^2);
R = mean(abs(sn).^4)/mean(abs(sn).^2);
Ri = Ri/sqrt(Ri^2+Rr^2);
Rr = Rr/sqrt(Ri^2+Rr^2);

%% MSEI
W_msei = zeros(Nf,1);
W_msei((Nf+1)/2) = 1;
muMSEI  = 0.0004;%%16QAM时的步长选取
muQ  = 0.0004;%%16QAM时的步长选取
R1 = xn(1:Nf);
x=xn(1:17);
n=length(x);
m=n-1;
rx=xcorr(x);
R_m=toeplitz(rx(n:n+m))/n;%%自相关矩阵
Q = inv(R_m);
for ik = 1:L-Nf
    X_msei(:,ik) = fliplr(xn(ik:ik+Nf-1));
    Y_msei(ik) = W_msei'*X_msei(:,ik);
    Yr_msei = real(Y_msei(ik));
    Yi_msei = imag(Y_msei(ik)); 
    Er_msei(ik) = Yr_msei*(Rr-Yr_msei^2);
    Ei_msei(ik) = Yi_msei*(Ri-Yi_msei^2);
    E_msei = Er_msei+1i*Ei_msei;
    W_msei = W_msei + muMSEI*Q*conj(E_msei(ik))*X_msei(:,ik);%%存疑
    Q = (1/(1-muQ))*(Q-muQ*Q*conj(X_msei(:,ik))*conj(X_msei(:,ik)')*Q/(1-muQ+muQ*conj(X_msei(:,ik)')*Q*conj(X_msei(:,ik))));
end

figure();plot(sn(30000-Nf+1:end),'.');title('均衡前');
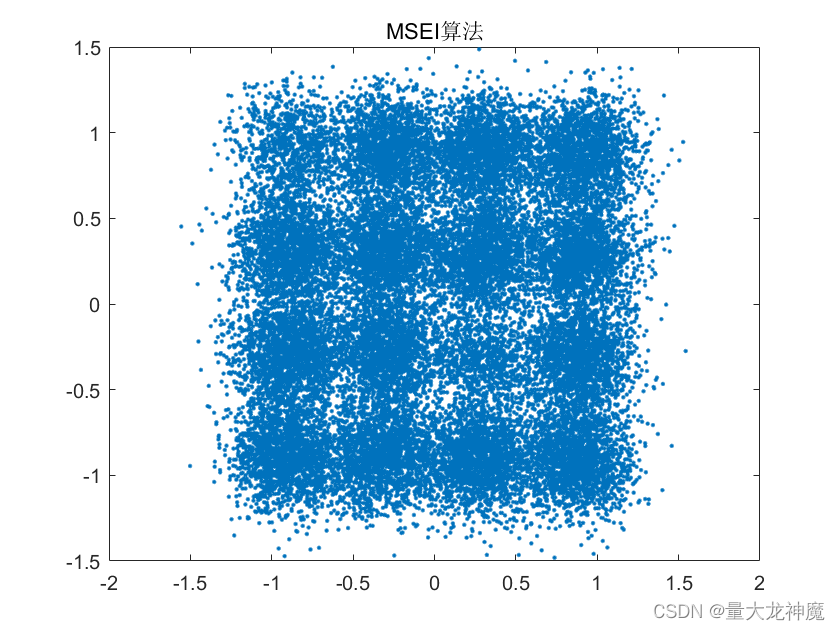
figure();plot(Y_msei(30000:end),'.');title('MSEI算法');