【推荐系统1---评价指标ACC、Recall、Precision、F1 score、HR、MRR、NDCG】

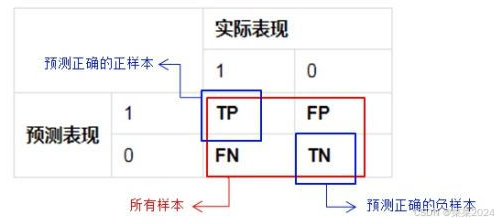
1.混淆矩阵

TP：True&Positive（positive表示正样本，true表示预测正确。即预测为正样本，实际也是正样本）
FP：False&Positive（positive表示正样本，false表示预测错误，即预测为正样本，实际也是负样本）
FN：False&Negative（negative表示负样本，false表示预测错误，即预测为负样本，实际是正样本）
TN：True&Negative（negative表示负样本，true表示预测正确，即预测为负样本，实际也是负样本）
（T和F表示的预测的准不准，P和N代表是预测的结果）

• 准确率accuracy：预测正确的个数/总样本数，如果用混淆矩阵里的数据表示，就是（TP+TN）/（TP+FP+FN+TN）
• 精确率precision，预测为1的样本中实际为1的频率，也就是TP/（TP+FP）。精确率代表的是正样本结果中的预测准确度。
• 召回率recall,又叫查全率，实际为1的样本中被预测为1的频率，其公式为TP/（TP+FN）。这个比率反映了正样本被正确预测的比例,召回率低说明有大量正样本没有被正确分类。
• F1分数在不同阈值（预测分数大于多少认为分类正确）下绘制出来，就得到了P-R曲线（精确率-召回率曲线)
• F1score=(2precisionrecall)/(precision+recall)
• F1分数其实是精确率和召回率的调和平均（倒数之和的平均值的倒数）
• 真正率TPR就是召回率recall, TPR=TP/（TP+FN）=TP/P,假正率（1-特异度）FPR=FP/（FP+TN）=FP/F
• ROC（receiver operating characteristic curve）是一条曲线。该曲线涉及两个指标：真正率（TPR）和假正率（FPR）。FPR为x轴，TPR为y轴画图，就得到了ROC曲线。

假设有6个样本【A,B,C,D,E,F】
以@5为例, 给出预测的、真实的用户将要交互的物品：
真实的：[A, B, C, D, E]
预测的：[A, C, B, E, F]
则： TP = 4（ABCE） TN = 0 FP = 1（F） FN = 1（D）

1. Accuracy（准确率）–ACC
   预测正确的样本在所有样本中的比例,（TP+TN）/（TP+FP+FN+TN）
   ACC = (4 + 0) / 6 = 0.67

2. Recall（召回率、查全率）
   实际为1的样本中被预测为1的频率，TP/（TP+FN）
   recall=4/(4+1)=0.8

3. Precision（精确率、查准率）
   预测为1的样本中实际为1的频率，也就是TP/（TP+FP）
   precision=4/(4+1)=0.8

4. F1 score（精确率与召回率的调和均值）
   F1score=(2precisionrecall)/(precision+recall)
   F1 = 2 (0.8 * 0.8) / (0.8 + 0.8) = 0.8

2.命中率HR–Hit Ratio

预测结果列表中预测正确的样本占所有样本的比例，即用户想要的项目有没有推荐到，强调预测的“准确性”。

S为样本的数目，可以理解为用户的需求项的数目。 hit(i)用于表述第 i 项需求项是否包含在模型推荐的项目列表中。若在，则其值为1；否则为0

HR = 4 / 5 = 0.8 （要访问的有5个，成功预测了4个，因此为0.8）
针对 A 的话，HR = 1
针对 D 的话，HR = 0

实际中是得到各个预测的概率

import torch
import math

T = torch.tensor([3])
P = torch.tensor([0.1, 0.2, 0.15, 0.25, 0.3])
# T中表示的是用户的需求项，3表示第3项。
# P中表示的是概率值，即为对应index项被推荐的概率。
# 如0.1的index为0，表示第0项被推荐的概率为0.1
# T和P中仅包含一次推荐过程：用户需要的第3个项目在推荐列表中排在第2位。
# 第2位是指将P按概率值对index进行排位的结果(4, 3, 1, 2, 0)的第二个元素。



def HR(truth, pred, N):
    """
    Hit Ratio
    truth: the index of real target (from 0 to len(truth)-1)
    pred: rank list
    N: top-N elements of rank list
    """
    top_N = pred.squeeze()[:N]
    hit_N = 1.0 if truth in top_N else 0.0
    return hit_N


p = torch.argsort(P.unsqueeze(0), dim=1, descending=True)
hr = HR(T, p, 3)
print(f'HR={hr}\n')

->> HR=1.0

3.平均倒数秩MRR–Mean Reciprocal Rank

平均结果中的排序倒数，表示待推荐的项目是否放在了用户更显眼的位置，强调“顺序性”

S为样本的数目，可以理解为用户的需求项的数目。
pi为第 i 项需求项在模型推荐的项目列表中的位置。若第 i 个需求项不在推荐列表中，则 1/pi为0.
针对 A 的话，MRR = 1 / 1 = 1.0
针对 B 的话，MRR = 1 / 3 = 0.33

import torch
import math

T = torch.tensor([3])
P = torch.tensor([0.1, 0.2, 0.15, 0.25, 0.3])
# T中表示的是用户的需求项，3表示第3项。
# P中表示的是概率值，即为对应index项被推荐的概率。
# 如0.1的index为0，表示第0项被推荐的概率为0.1
# T和P中仅包含一次推荐过程：用户需要的第3个项目在推荐列表中排在第2位。
# 第2位是指将P按概率值对index进行排位的结果(4, 3, 1, 2, 0)的第二个元素。


def MRR(truth, pred, N):
    """
    Mean Reciprocal Rank
    truth: the index of real target (from 0 to len(truth)-1)
    pred: rank list
    N: top-N elements of rank list
    """
    top_N = pred.squeeze()[:N]
    if truth not in top_N:
        rr_N = 0.0
    else:
        i = top_N.numpy().tolist().index(truth)
        rr_N = 1 / (i + 1) # index从0开始
    return rr_N


p = torch.argsort(P.unsqueeze(0), dim=1, descending=True)
mrr = MRR(T, p, 3)
print(f'MRR={mrr}\n')

->> MRR=0.5

4.归一化折现累积增益NDCG–Normalized Discounted Cumulative Gain

推荐系统通常为某用户返回一个 item 列表，假设列表长度为 K，这时可以用 NDCG@K 评价该排序列表与用户真实交互列表的差距。 强调的是用户的需求项在模型推荐列表中的位置，越靠前越佳。

S为样本的数目，可以理解为用户的需求项的数目。 pi为第i 项需求项在模型推荐的项目列表中的位置。若第i 个需求项不在推荐列表中，则1/(log2(pi+1)) 为0.

针对 A 的话，NDGG = 1 / log2(1+1) = 1.0
针对 B 的话，NDGG = 1 / log2(3+1) = 0.5

import torch
import math

T = torch.tensor([3])
P = torch.tensor([0.1, 0.2, 0.15, 0.25, 0.3])
# T中表示的是用户的需求项，3表示第3项。
# P中表示的是概率值，即为对应index项被推荐的概率。
# 如0.1的index为0，表示第0项被推荐的概率为0.1
# T和P中仅包含一次推荐过程：用户需要的第3个项目在推荐列表中排在第2位。
# 第2位是指将P按概率值对index进行排位的结果(4, 3, 1, 2, 0)的第二个元素。


def NDCG(truth, pred, N):
    """
    Normalized Discounted Cumulative Gain
    truth: the index of real target (from 0 to len(truth)-1)
    pred: rank list
    N: top-N elements of rank list
    """
    top_N = pred.squeeze()[:N]
    if truth not in top_N:
        ndcg_N = 0.0
    else:
        i = top_N.numpy().tolist().index(truth)
        ndcg_N = 1 / (math.log2((i+1)+1))
    return ndcg_N


p = torch.argsort(P.unsqueeze(0), dim=1, descending=True)
ndcg = NDCG(T, p, 3)
print(f'NDCG={ndcg}\n')

->> NDCG=0.6309297535714575