线性代数（一）—— 行列式

最新推荐文章于 2025-03-08 23:07:23 发布

君一兮

最新推荐文章于 2025-03-08 23:07:23 发布

阅读量4.2k

点赞数 1

分类专栏：线性代数文章标签：线性代数矩阵算法

本文链接：https://blog.csdn.net/qq_45645521/article/details/123471640

版权

1 篇文章

订阅专栏

本文详细介绍了线性代数中的行列式概念，包括二阶三阶行列式、N阶行列式的计算方法和性质。重点讲解了行列式的展开、转置性质、行列式值的计算技巧，如按行展开、上三角行列式计算，以及拉普拉斯定理。此外，还讨论了特殊类型的行列式，如对称行列式和反对称行列式，并介绍了克莱姆法则在解线性方程组中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

引言

本专栏主要根据宋浩老师的线性代数视频梳理线性代数的知识点，再根据博主考研过程中做题进行补充说明

行列式一定是方的
$\left| \begin{array}{cccc} 1 & 0 & 0 \\ 2 & 1 & 3\\ 0 & 3 & 1 \end{array} \right|$
从左向右对角线是主对角线 $\left| \begin{array}{cccc} 1 & & \\ & 1 & \\ & & 1 \end{array} \right|$
从右向左对角线是次对角线 $\left| \begin{array}{cccc} & & 0\\ & 1 & \\ 0& & \end{array} \right|$
排列： $1 ， 2 ， 3 ， \dots \dots ， n$ 组成的一个有序数组叫n级排列，中间不能缺数
- 3级排列： $123 ， 132 ， 213 ， 231 ， 312 ， 321$
逆序：大数排在小数前面
逆序数：逆序的总数
奇/偶排列：逆序数为奇/偶
标准排列： $1234 \dots \dots n$
对换：交换排列中的两个数
- 做一次对换，排列奇偶性改变

按行展开
- 行取标准排列
- 列标取排列的所有可能，从不同行不同列取出 $n$ 个元素相乘
- 共有 $N!$ 项
- 每一行的符号由列标排列的奇偶性决定，偶正奇负
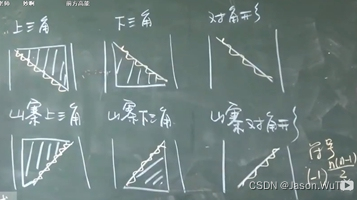
下三角行列式
$\left| \begin{array}{cccc} 1& 0& 0\\ 1& 1 & 0\\ 1 &1 &1 \end{array} \right|$
- 右上方三角形区域元素全部为0
- 下三角行列式 = 主对角线元素相乘
上三角行列式
$\left| \begin{array}{cccc} 1& 1& 1\\ 0& 1& 1\\ 0 &0 &1 \end{array} \right|$
- 左下方三角形区域元素全部为0
- 上三角行列式 = 主对角线元素相乘
对角线行列式
$\left| \begin{array}{cccc} 1& & \\ & 1 & \\ & &1 \end{array} \right|$
- 只有主对角线上有数
副对角线行列式
$\left| \begin{array}{cccc} & & 1\\ & 1& \\ 1& & \end{array} \right|$
- 副对角线行列式 = $1)^{n*(n-1)}*副对角线元素相乘$
三角行列式总结
行列式的三种定义
- 按行展开，符号由列标排列决定
- 按列展开，符号由行标排列决定
- 胡乱展开，符号由行标排列逆序数和列标排列逆序数之和决定
  $1)^{N(i1,i2,……,iN)+N(j1,j2,……,jN)}, i：行标，j：列标$

行列式对行成立的性质对列也成立

若行列式某一行元素都可以表示为两项和，则行列式等于两个行列式相加
$\left| \begin{array}{cccc} 1+2 & 2+3 & 1+3 \\ 2 & 1 & 3\\ 0 & 3 & 1 \end{array} \right| = \left| \begin{array}{cccc} 1 & 2 & 1 \\ 2 & 1 & 3\\ 0 & 3 & 1 \end{array} \right| +\left| \begin{array}{cccc} 2 & 3 & 3 \\ 2 & 1 & 3\\ 0 & 3 & 1 \end{array} \right|$