cs61b学习记录（二）

cs61b学习记录（二）

Lecture13 Generics, Autoboxing

Generic Methods

Lecture14 Exceptions, Iterators, Iterables

Exception

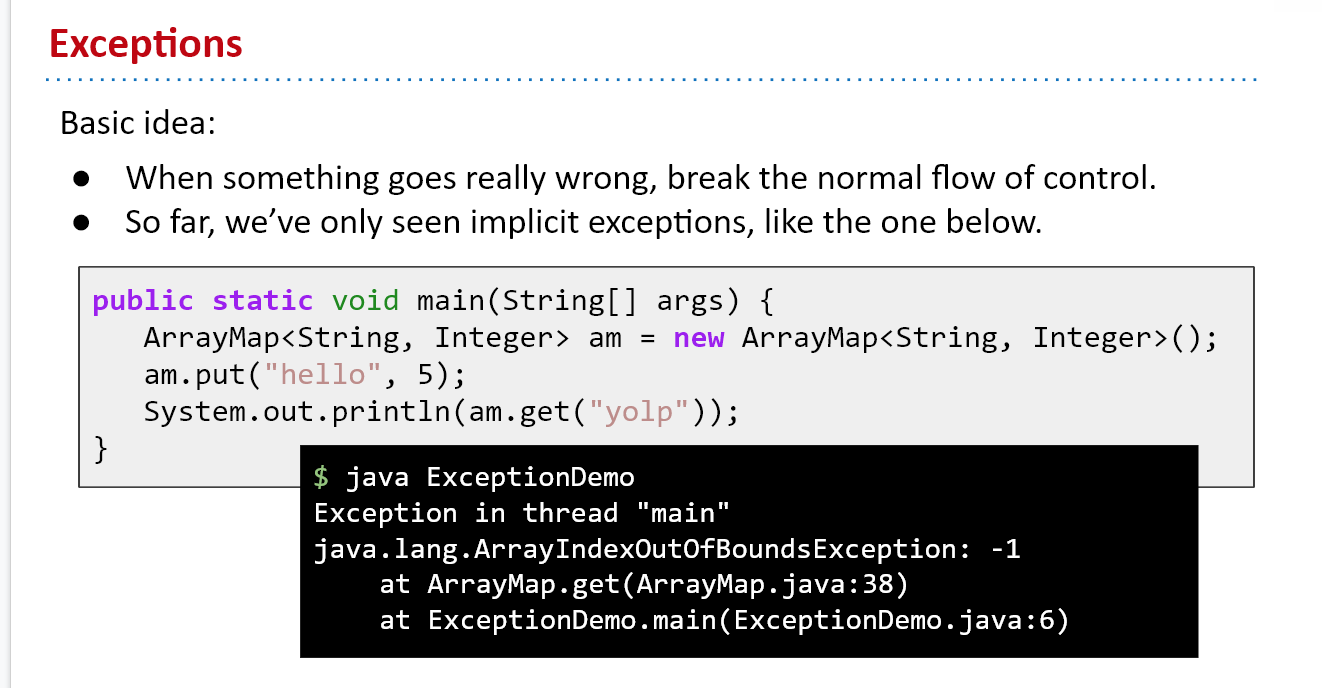
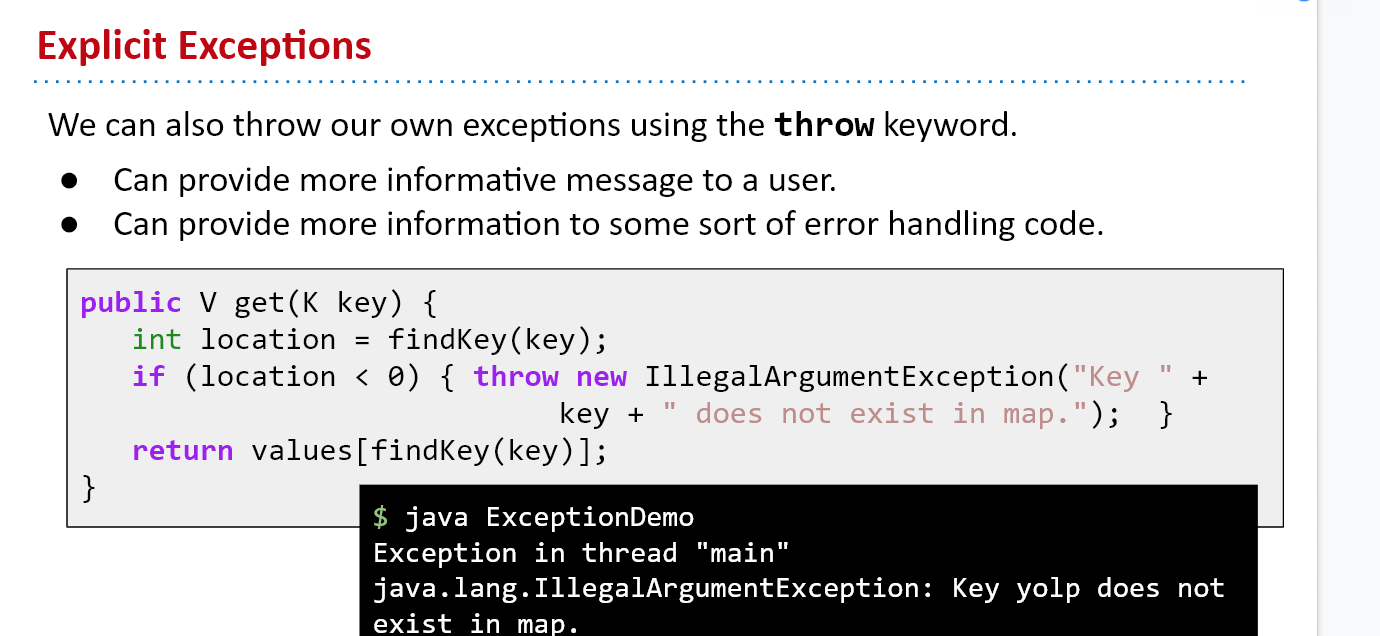
Exceptions cause normal flow of control to stop. We can in fact choose to throw our own exceptions. why is this better?

1. We have control of our code: we consciously decide at what point to stop the flow of our program
2. More useful Exception type and helpful error message for those using our code

we also use catch to prevent program from crashing

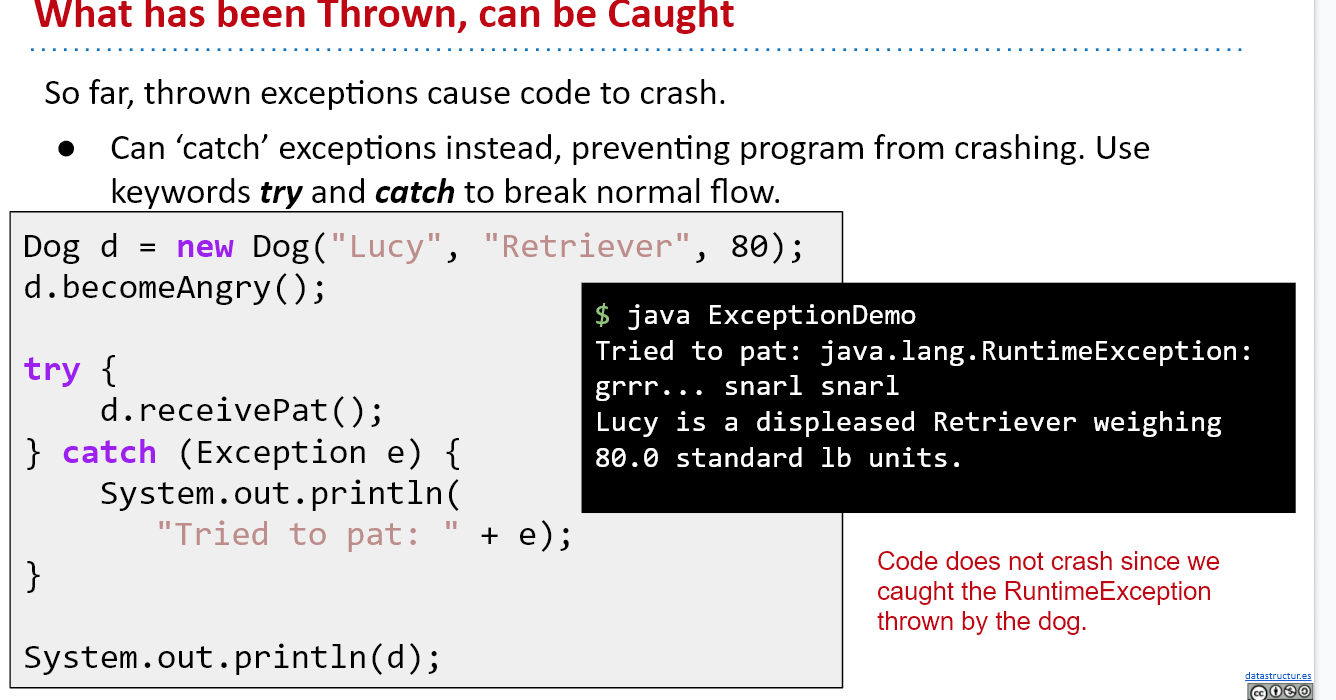
The philosophy of exceptions

To Keep error handling code separate from the real code！！！

To Keep error handling code separate from the real code！！！

To Keep error handling code separate from the real code！！！

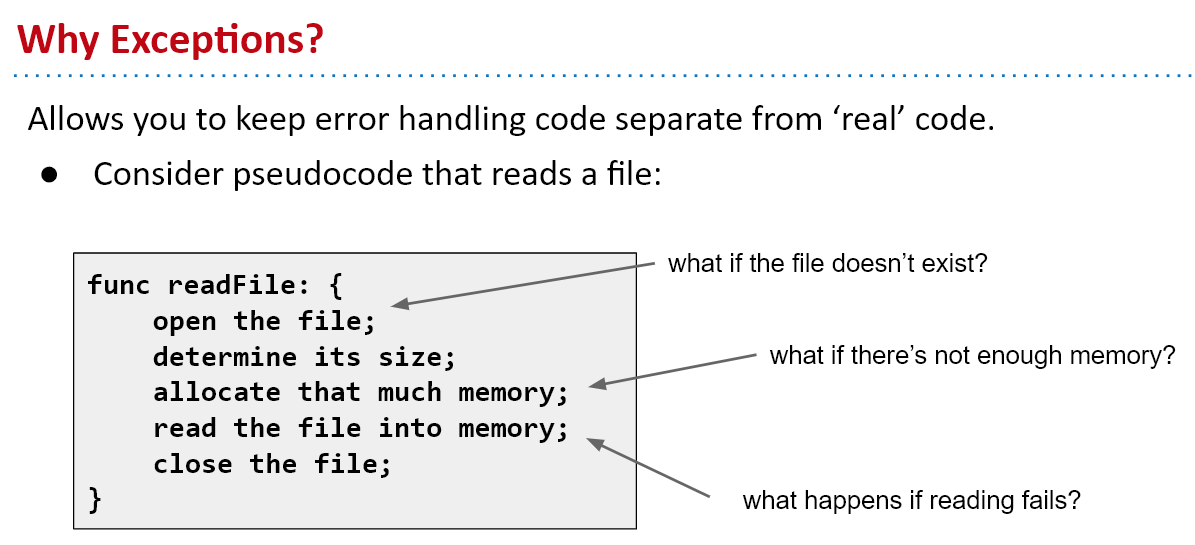
如果没有exception，我们也可以使用if else 完成exception的catch，但是这会打断流畅的代码，导致代码看起来非常的混乱。如右边的代码所示。

但是，使用了exception和catch后，代码的逻辑变得清晰（nice narrative）

your code really should be beautiful，it should feel like a story，the left one is a story

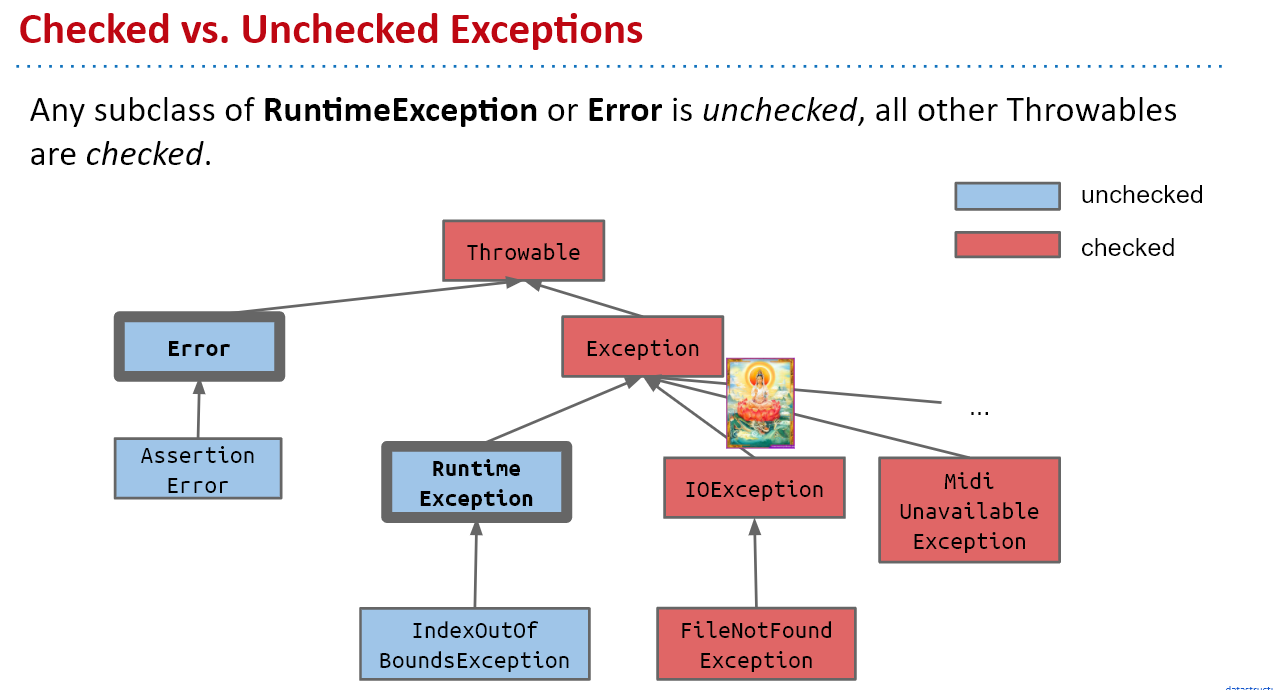
Checked vs. Unchecked Exceptions

类似IOException的属于checked exception，如果不处理这个exception（catch或throws抛给别人解决），编译器会不通过，因为这属于可避免（avoidable）的program crashes。

而RuntimeException属于Unchecked exception，可以不处理这个异常，即使我们知道它运行时一定会crash。

解决exception的两个方法：

• 直接catch
• throws，让这个函数自身变成一个异常，交给调用者处理

Reading8.1

Views

Views are an alternative representation of an existed object. Views essentially limit the access that the user has to the underlying object. However, changes done through the views will affect the actual object.

视图是对对象的另一种表达方式，本质上是限制用户对基本对象的访问，但是对视图做出的改变都是直接作用在实际对象上。

List<String> L = new ArrayList<>();
L.add(“at”); L.add(“ax”);
List<String> SL = L.subList(1, 4);
SL.set(0, “jug”);

subList方法实际上返回一个SubLIst对象，这个SubList对象继承了AbstractList类型，而AbstractList实现了List接口，所以SubList也是List类型。

public List<E> subList(int fromIndex, int toIndex) {
		.....
        return new SubList(this, fromIndex, toIndex);
    }

Private class Sublist extends AbstractList<Item>{
    Private int start end;
    Sublist(List parent，inst start, int end){...}
}

this指向调用subList方法的List对象，即方法实际作用的对象

public Item get(int k){return AbstractList.this.get(start+k);}
public void add(int l, Item x){AbstractList.this.add(start+k, x); end+=1}

所有通过subList方法返回的对象调用的方法实际上都是在调用this的方法，也就是调用subList对象的方法。本质上是在操作原对象。

Lecture15 Packages, Access Control, Objects

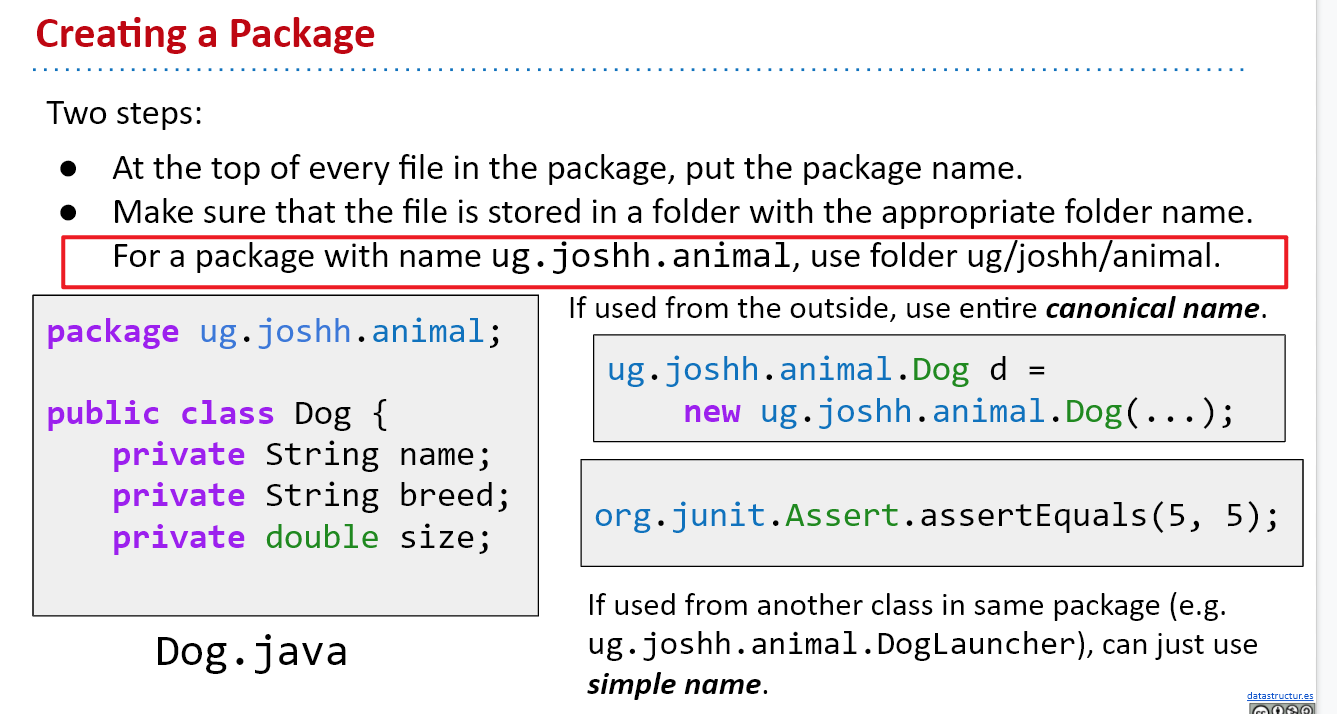
package的结构对应着工作目录中文件夹的结构

Default packages

Any Java class without an explicit package name at the top of the file is automatically considered to be part of the “default” package. However, when writing real programs, you should avoid leaving your files in the default package (unless it’s a very small example program). This is because code from the default package cannot be imported, and it is possible to accidentally create classes with the same name under the default package.

• Moving a class into a package

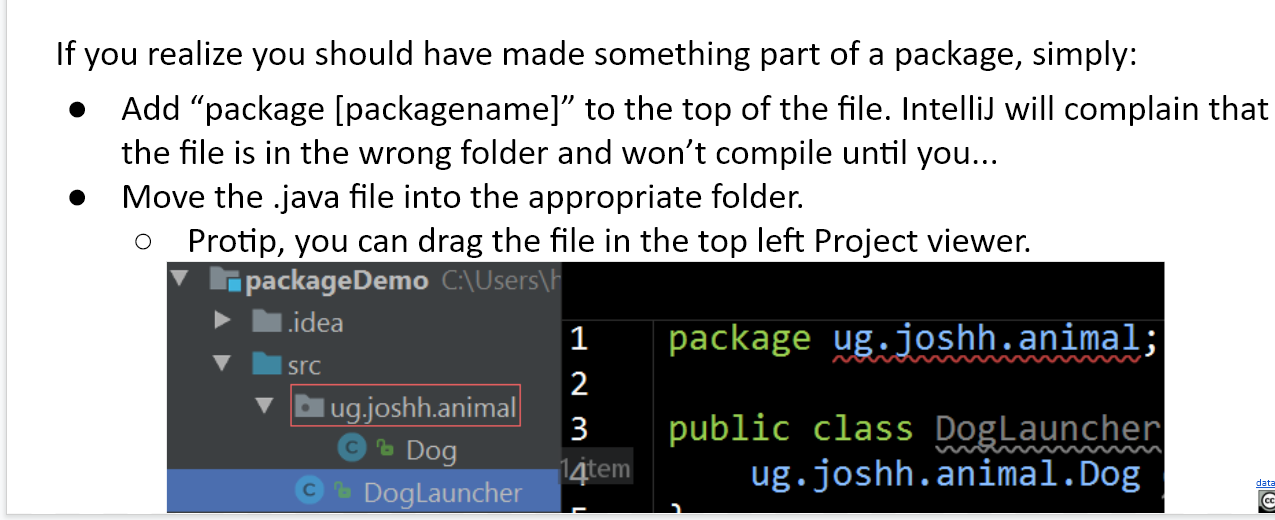
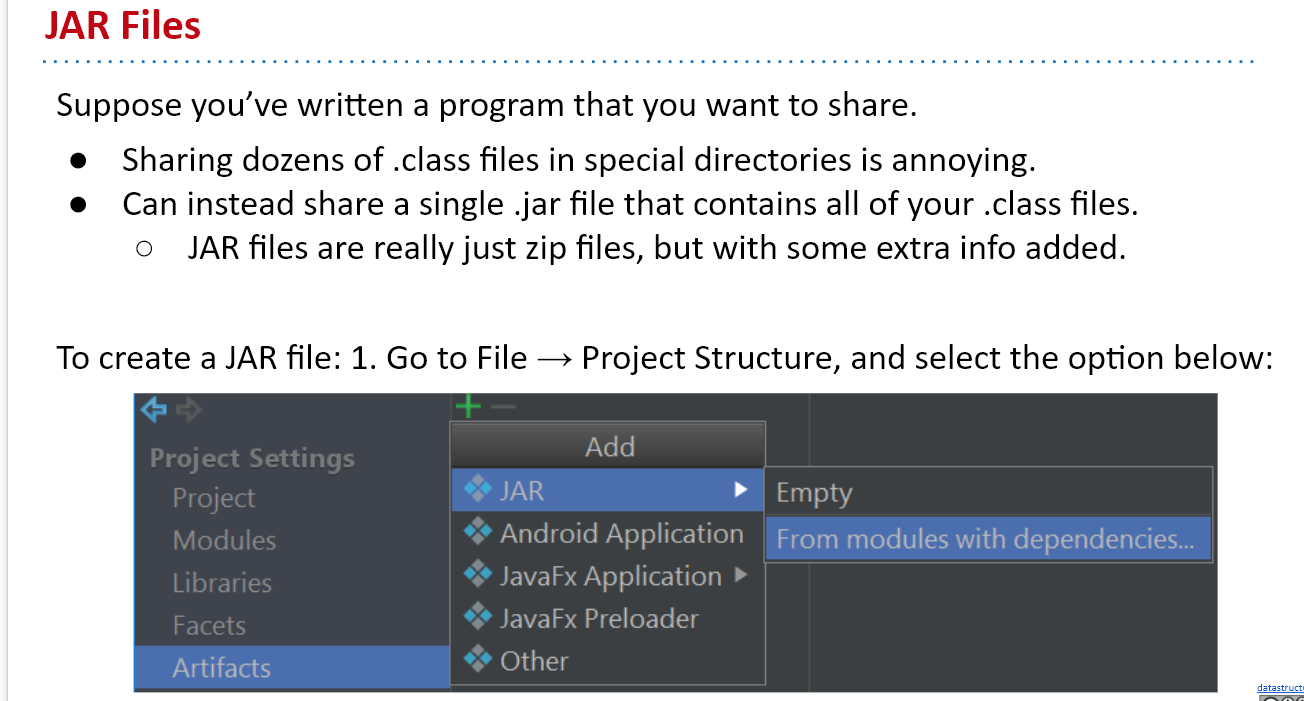
JAR Files

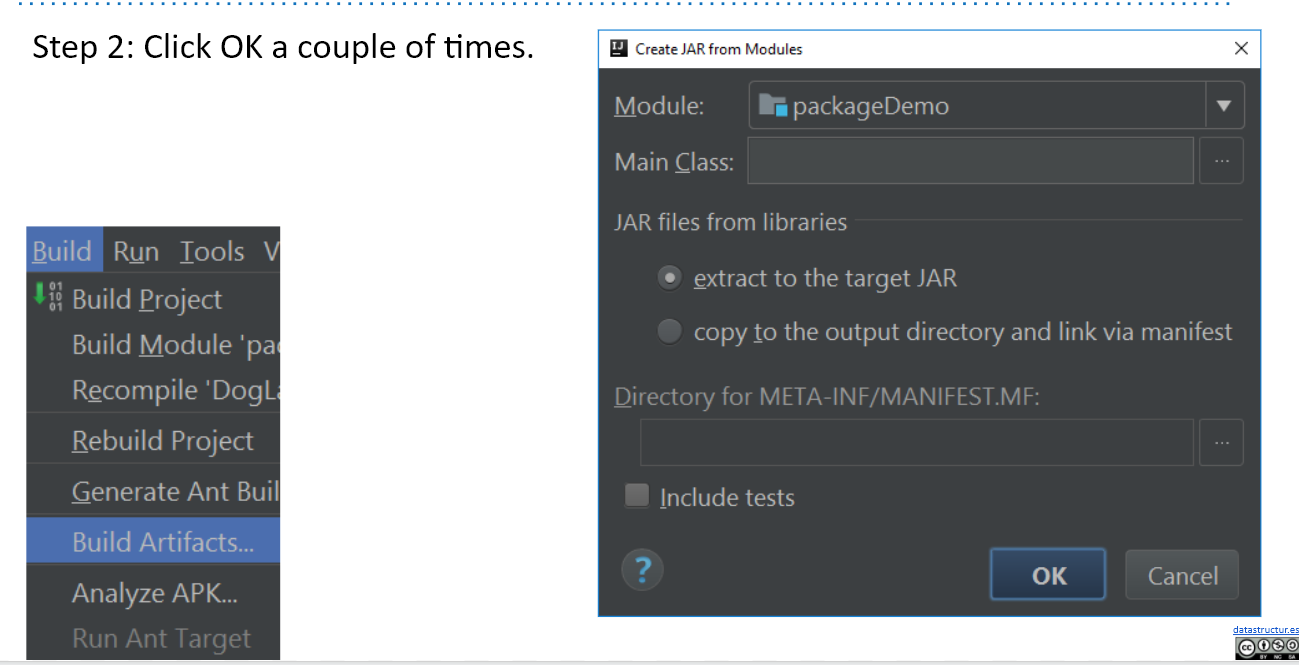
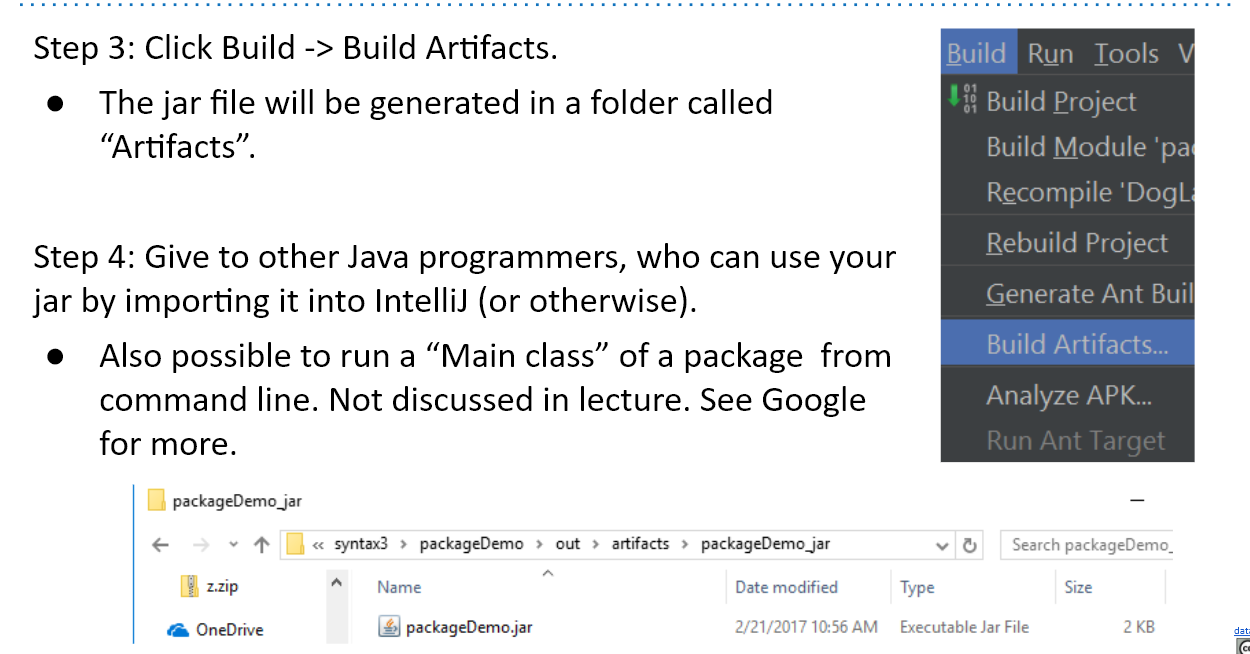
build system

Access Control

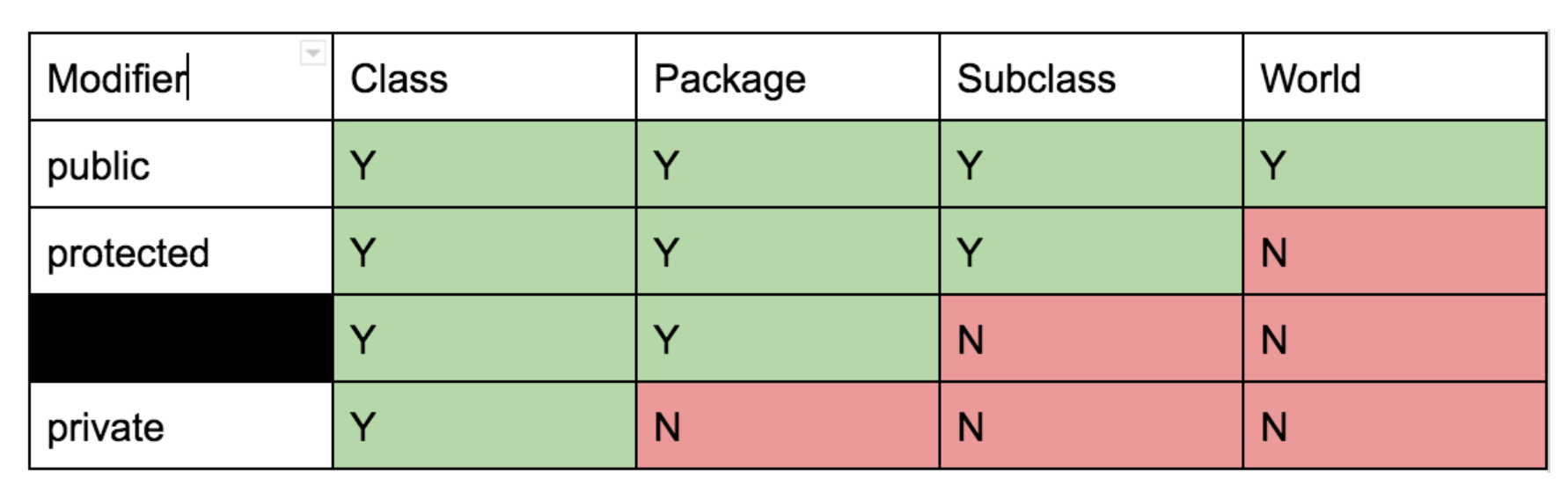
Private Only code from the given class can access private members. It is truly private from everything else, as subclasses, packages, and other external classes cannot access private members

Package Private This is the default access given to Java members if there is no explicit modifier written. Package private entails that classes that belong in the same package can access, but not subclasses!

Protected classes within the same package and subclasses can access these members

Public This keyword opens up the access to everyone!

java中的访问控制与C++中略有差别，在private和protected之间实际上多了一级package

访问控制不仅可以针对成员，还可以针对类。只有两个层次：public和package-private。

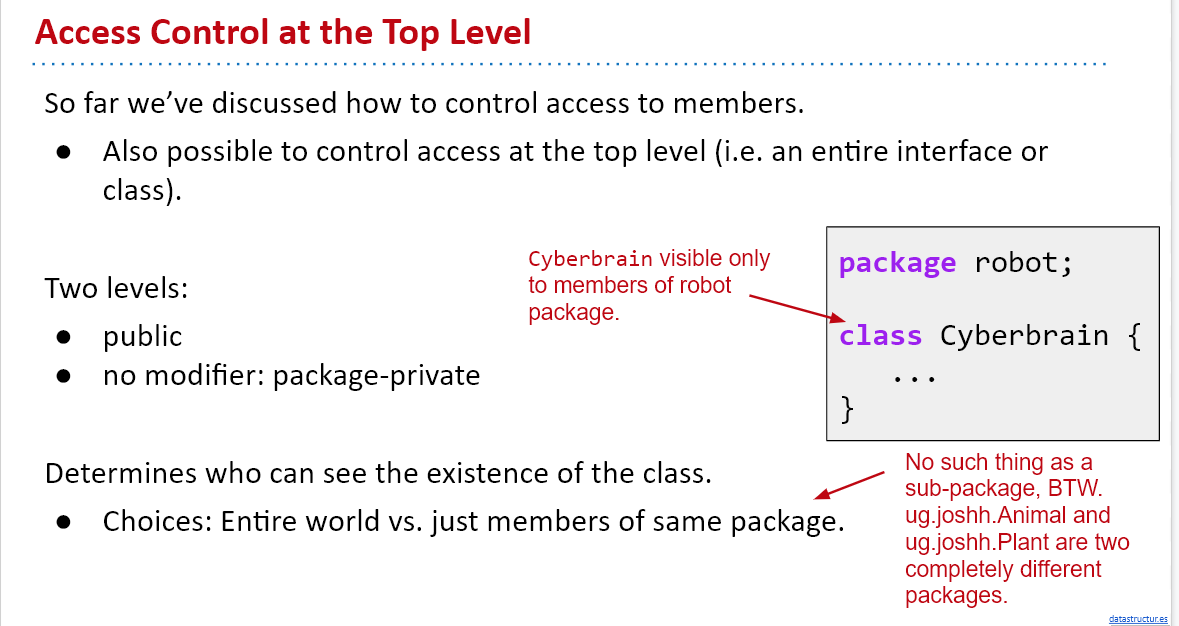
对于没有modifier的类就是package-private，对该package以外的东西不可访问。

Lecture17 Asymptotics I

根据selection sort，我们排序一个大小为n的数组需要n^2/2次操作。

但是如果我们将数组对半分开，将左右两边分别排序，再将左右两个数组归并成一个数组，我们发现，这样只需要

n^2/4+n

我们可以继续划分下去

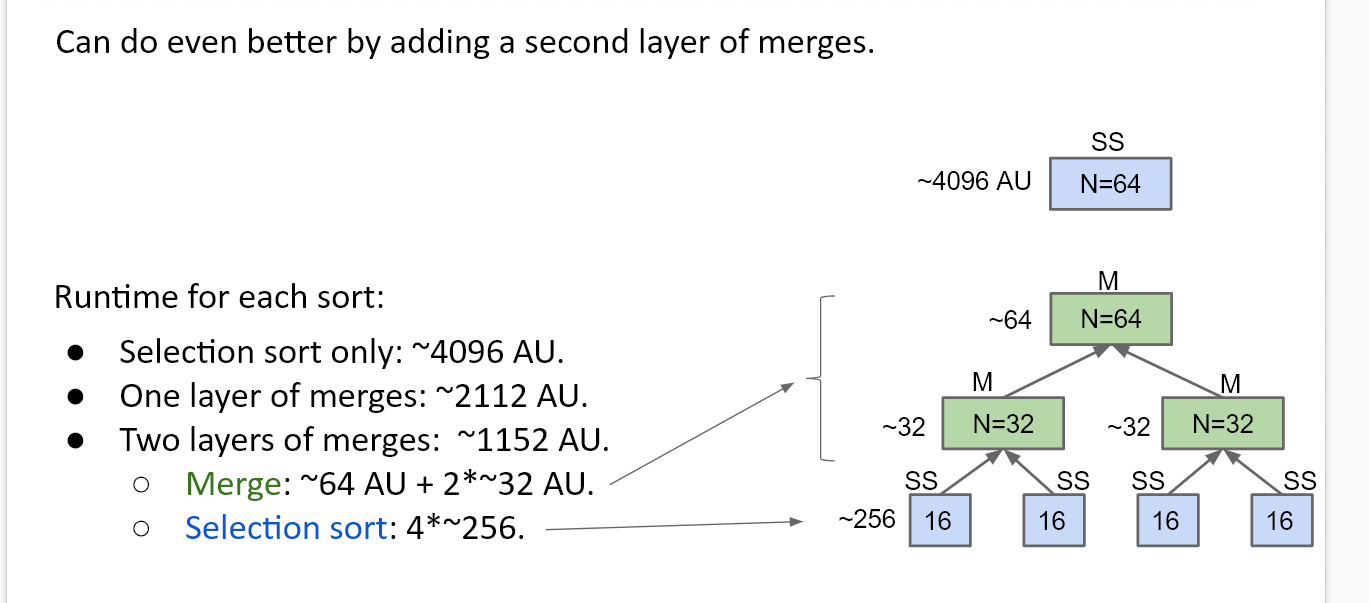
直到分到只剩一个元素的数组，此时我们不需要排序，只需要将所有的数组自底向上归并就行了。

归并成一个大小为N的数组操作N次，而每一层的数组大小的总和都是N，总共的操作次数是N乘以层数，而层数等于lgN，所以复杂度为O(NlgN)

Lecture20 Disjoint Sets

this chapter will be a chance to see how an implementation of a data structure evolves. We will discuss four iterations of a Disjoint Sets design before being satisfied: Quick Find → Quick Union → Weighted Quick Union (WQU) → WQU with Path Compression. We will see how design decisions greatly affect asymptotic runtime and code complexity.

该问题本质上是connect和isConnected两个方法，首先调用connect，将输入的点连接起来。再调用isConnected，判断某两个点是否相连。本节内容主要围绕这两个操作的改进与升级。

如何判断两个点是否相连？如果只是对每两个点之间的连线进行判断，这个效率是非常低下的。我们可以将所有连接过的点划分到同一个连通分支中，当我们要判断两个点是否相连时，只需要判断这两个点是否属于同一连通分支即可。

ListOfSet

如何快速判断该点属于哪一个连通分支，追踪该点所属的集合？

the most intuitive idea：

这种方法在connect时需要从头到尾将List中的所有Set找一遍，才能找到连接的对象，最差的情况：当List中没有任何元素相连时，找N次，所以performance：O(N)

isConnected同理，也需要从头到尾把所有的集合都找一遍才能找到要连接的元素。O(N)

将同一个连通分支的元素放在同一个Set中，对每一个连通分支（Set），只需要一次操作就可以判断该元素属不属于这个连通分支。然而，我们无法知道要连接的元素所在的位置。对于每一次连接和判断是否连接我们都需要从头到尾将List中的所有集合找一遍，判断该元素是否属于该集合。

所以，我们不仅需要能够快速得知某一元素是否属于某一集合，还需要快速找到该元素所在的位置。

针对快速随机访问，我们应该使用数组：

QuickFind

数组的下标对应着每一个元素，属于同一连通分支的元素对应的数组位置上的值相同，实现了快速得知某一元素是否属于某一集合；同时，元素的值作为数组的下标，实现了快速访问某一个元素。

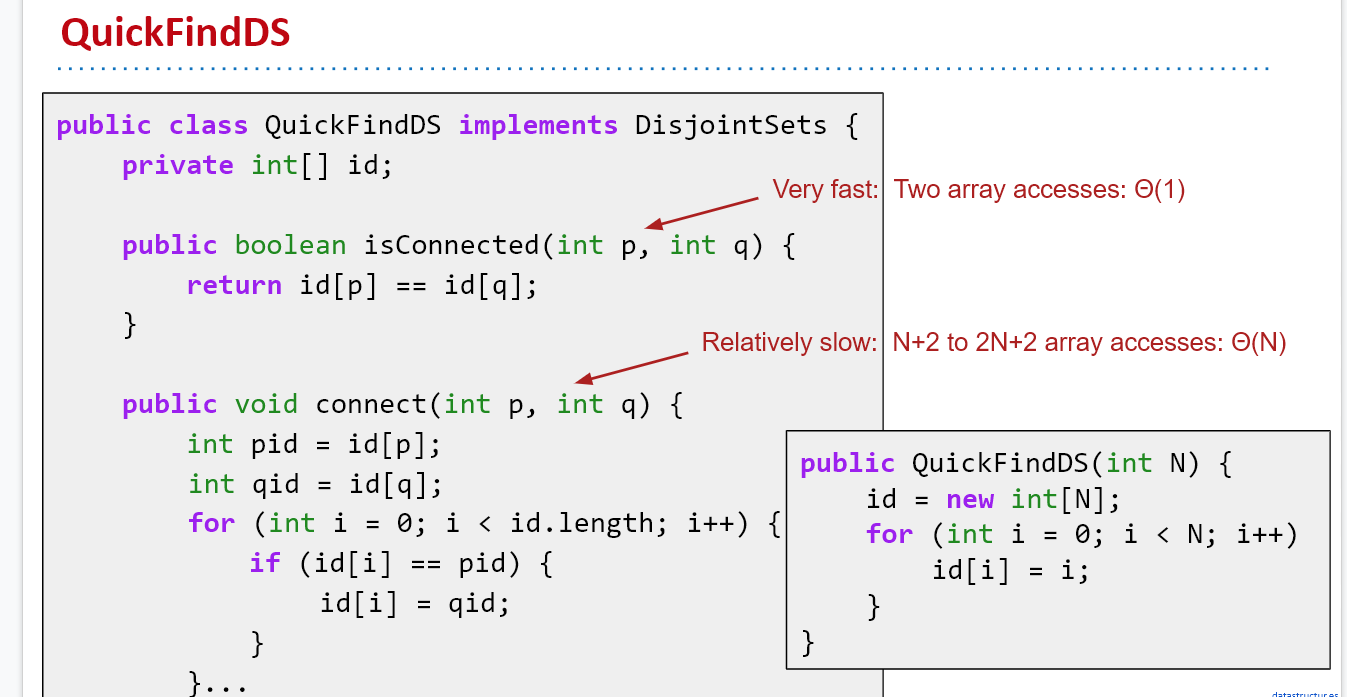
该方法判断是否连接只需要判断两个元素所在数组位置上的值是否相同即可，一次操作

但是每一次connect需要将数组从头到尾扫一遍，改变所有处于同一连通分支的元素的值修改，即将所有和被连接元素的值相同的元素的值修改。不管什么情况都需要n次操作。Theta N。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xVReN2cG-1616906278282)(https://cdn.jsdelivr.net/gh/BoL0150/imgbed@main/image-20210315223529779.png)]

可见这种方式的连接操作非常的慢，但是查找的速度很快，所以称之QuickFind

QuickUnion

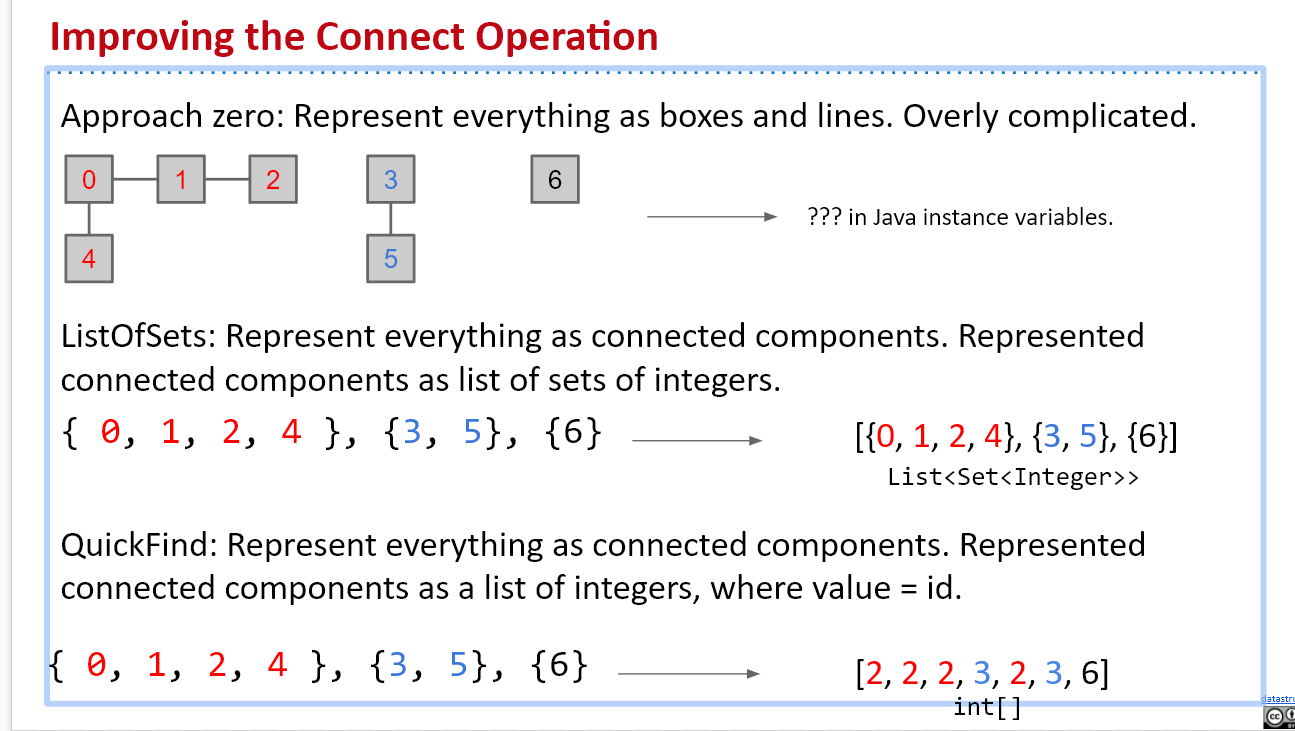
QuickFind的问题在于连接的操作非常慢，需要一个一个地修改同一个连通分支中的所有元素的值。

如果我们只需要修改同一个连通分支中的某一个数就可以改变整个连通分支所有节点的集合，从而连接两个集合，就可以解决这个问题

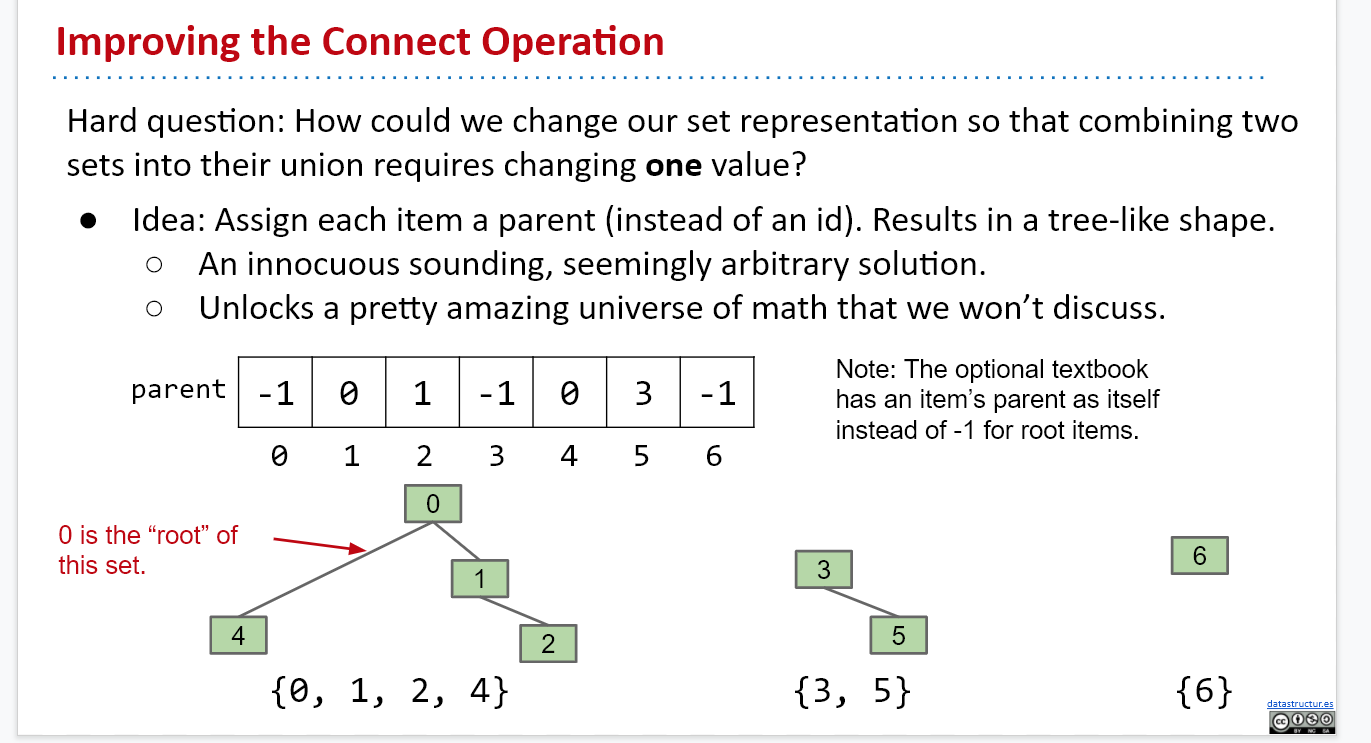
解决方法：用树状的结构表示同一个集合，只需要改变根节点的指向就可以改变整个集合的指向。

对于connect操作，需要先找到被连接的两个元素的根节点，然后合并根节点。这个速度比之前要快很多。

对于isConnected操作，同样需要找到被连接的两个元素的根节点，判断根节点是否相同，这个速度比之前反而要慢一些。

然而，当形成的树是不平衡的（比如高的树挂在矮的树上，如果这种情况经常发生，树就会极不平衡），查找根节点的速度将会变得非常慢。此时connect和isConnected方法速度降低，甚至比之前的方法还要慢。

Weighted Quick Union

用树来表示一个集合，在最好的情况下，合并和查找的速度只需要lgN，但是在极端情况下，如果树是不平衡的，将退化成N。所以我们需要避免极端情况：将小的树挂在大的的树上。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nNKePisE-1616906278293)(https://cdn.jsdelivr.net/gh/BoL0150/imgbed@main/image-20210316105155512.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aadHApCV-1616906278298)(https://cdn.jsdelivr.net/gh/BoL0150/imgbed@main/image-20210316105155512.png)]

为什么使用weight而不是height？

此时，connect和isConnected操作真正实现了lgN的复杂度。

Path Compression

我们发现，每一次寻找根节点时，沿途所有的节点的根节点都找到了。所以，我们可以将沿途所有的节点都直接指向根节点，这样，在下一次寻找时，路程就会短很多

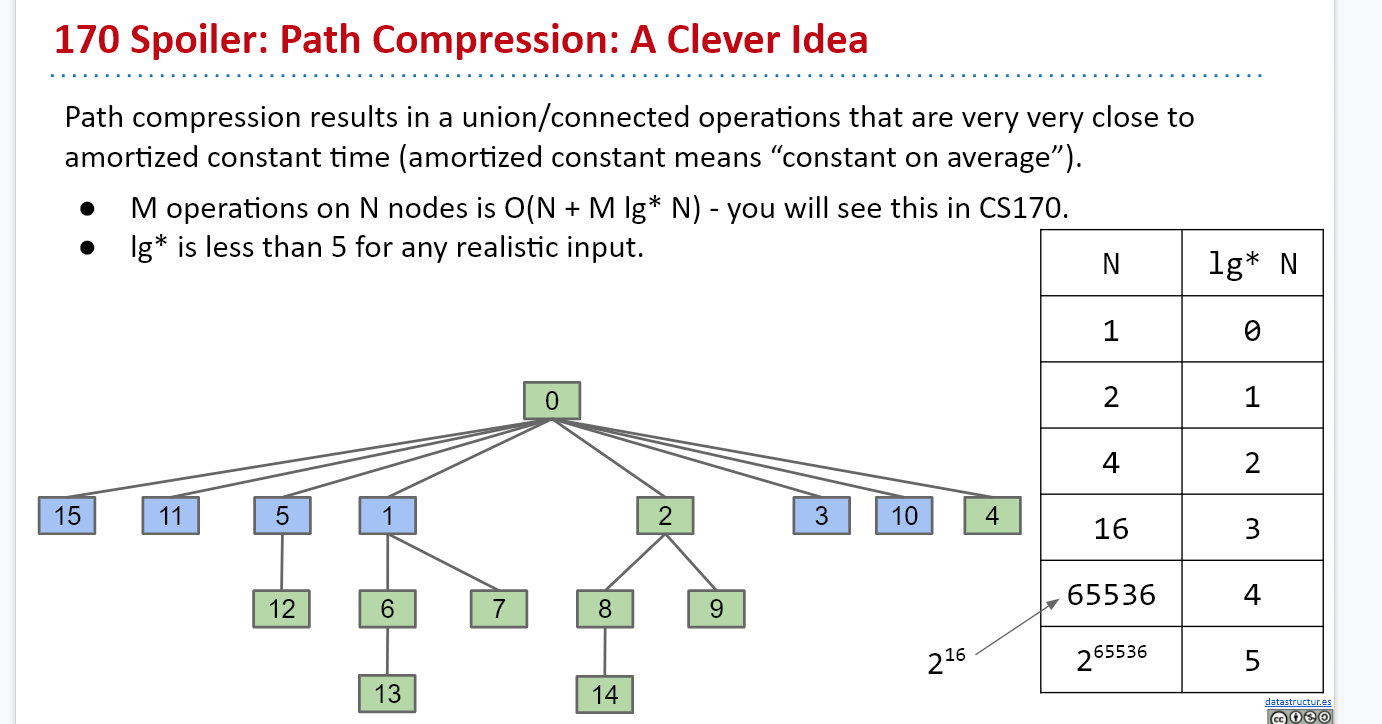
这样优化后，均摊下来，每一次connect和isConnected操作只需要查找lg*N次，这个数字几乎相当于常数。也就是说，执行M次connect和isConnected操作，只需要查找大概M次就行了。时间复杂度为O(N+Mlg *N)，几乎相当于O(N+M)

来，每一次connect和isConnected操作只需要查找lg*N次，这个数字几乎相当于常数。也就是说，执行M次connect和isConnected操作，只需要查找大概M次就行了。时间复杂度为O(N+Mlg *N)，几乎相当于O(N+M)