机器学习实战之SVM与二分类

最新推荐文章于 2023-11-28 21:24:46 发布
最新推荐文章于 2023-11-28 21:24:46 发布
阅读量6.2k 收藏 64
点赞数 21
分类专栏： 机器学习 文章标签： 支持向量机 机器学习 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_45749702/article/details/122132046
版权

文章目录

一、线性SVM

1.1 最大间隔与分类

在样本空间中寻找一个超平面, 将不同类别的样本分开，同时，这条线要与样本点有着尽可能大的间隔。那么，这条线就是在最边缘的两个样本点的中间，这些边缘的样本点就称为支持向量。
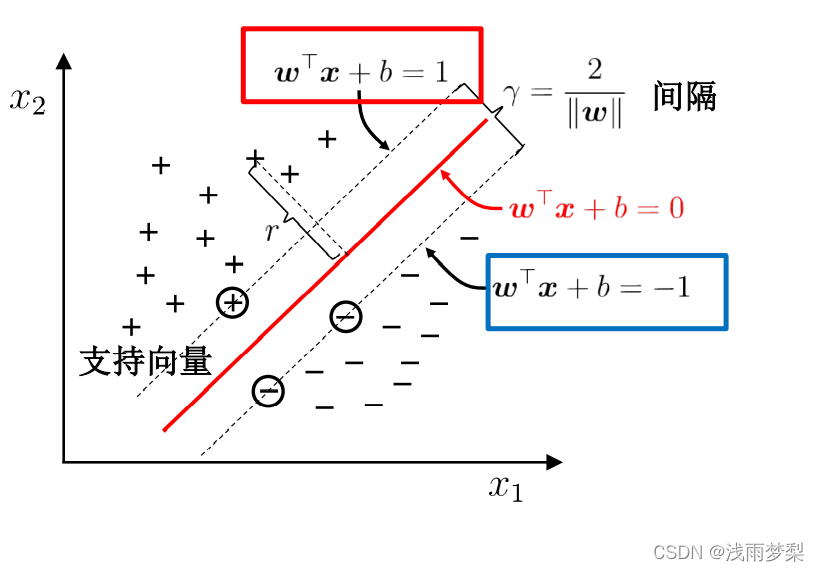
在这里插入图片描述
要找到最大间隔，就是求两点之间的距离。正负样本支持向量间的距离就等于两倍正样本到分类线的距离。
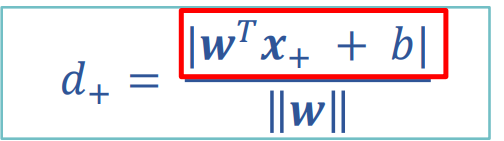
在这里插入图片描述
其中，分子=1
得到距离：
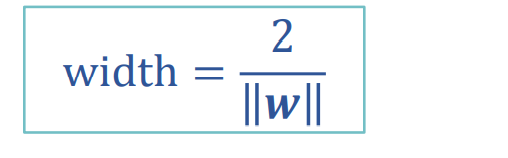
在这里插入图片描述
最终问题变成了求解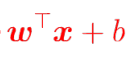在这里插入图片描述
上述已知支持向量的点的绝对值为1，则在它们后面的就应该>=1
如下公式易证：若得到的分类正确，那么yi的值与其待入值同向。
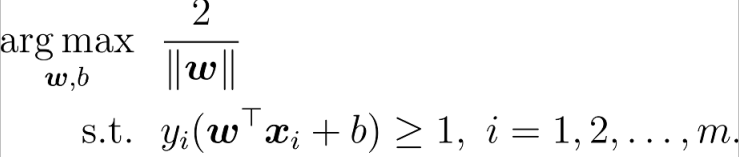
在这里插入图片描述
转为求最小值
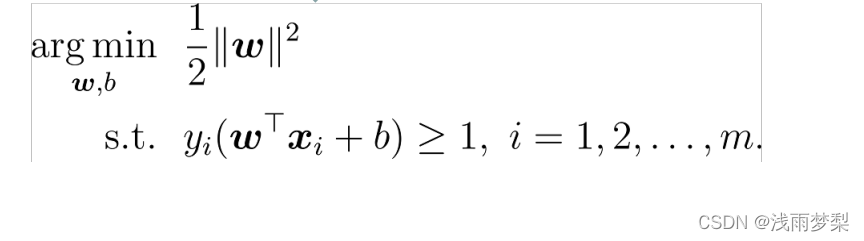
在这里插入图片描述

1.2 对偶问题

在约束条件下求最小值，使用拉格朗日乘数法
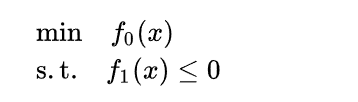
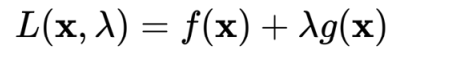
在这里插入图片描述
在这里插入图片描述
在SVM求解w最小值的情况下，得到以下步骤：

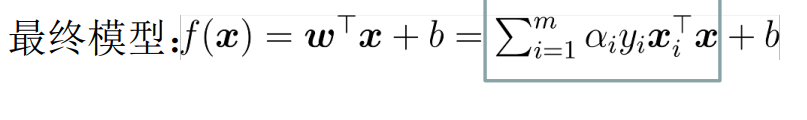
在这里插入图片描述
在这里插入图片描述
最后只剩下未知数αi

1.3 SMO算法流程

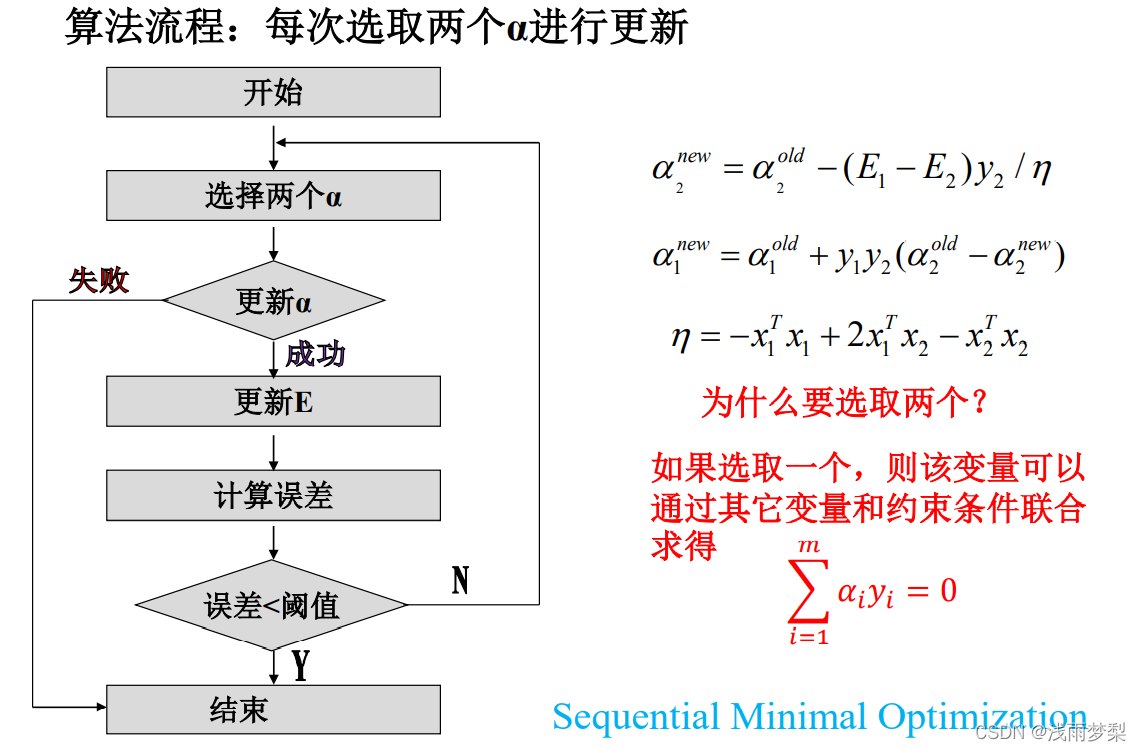
在这里插入图片描述
在这里插入图片描述
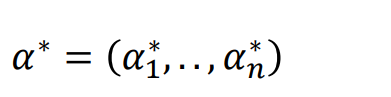
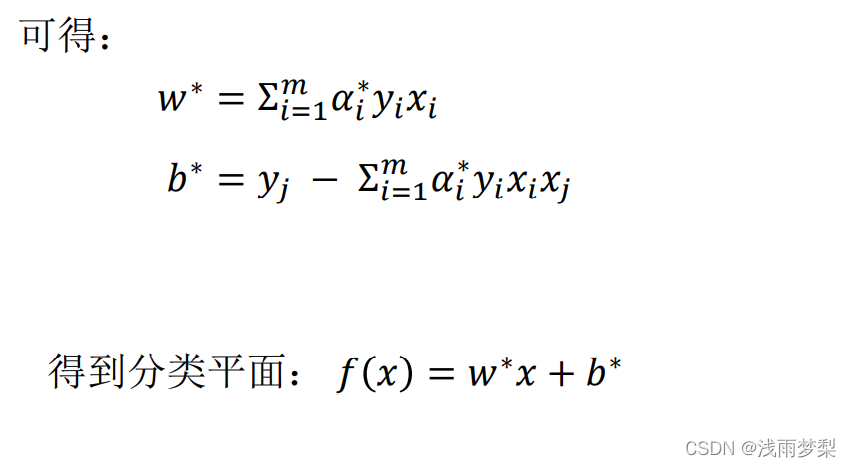
最后求解α在这里插入图片描述
在这里插入图片描述

二、 非线性SVM

2.1 核函数与核技巧

在线性不可分的情况下，选择一个核函数将其映射到高维空间使其线性可分
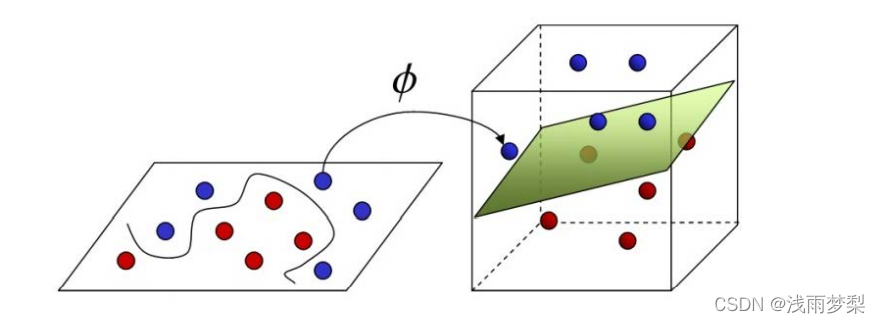
在这里插入图片描述
其中，ϕ是设样本x映射后的向量为ϕ(x), 得到划分超平面为f(x)=wTϕ(x)+b
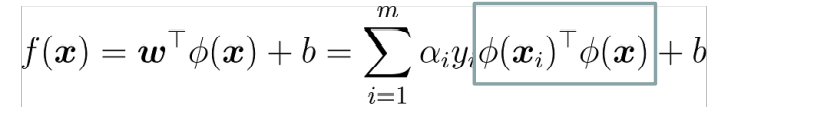
在这里插入图片描述
这样求解问题就分成了两步：
首先使用一个非线性映射将数据变换到一个特征空间F；
然后在特征空间使用线性学习器分类。
常见的核函数如下：
在这里插入图片描述

如果有一种方法可以在特征空间中直接计算内积<ϕ(x_i),ϕ(x)>，就像在原始输入点的函数中一样，就有可能将两个步骤融合到一起建立一个分线性的学习器，这样直接计算的方法称为核函数方法。
将内积替换成核函数的方式被称为核技巧(kernel trick)。

2.3 软间隔与正则化

实际应用中，很难选择合适的核函数，使样本在特征空间中线性可
分; 此外，线性可分的结果也很难断定是否是由过拟合造成的。于是引入“软间隔”的概念, 允许SVM在一些样本上不满足约束。
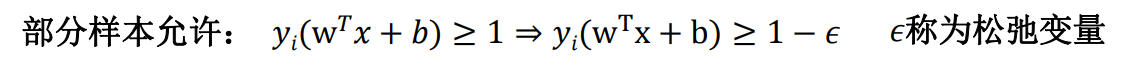
在这里插入图片描述
在这里插入图片描述
在求解最大化间隔的同时, 让不满足约束的样本应尽可能少，最终转为求解
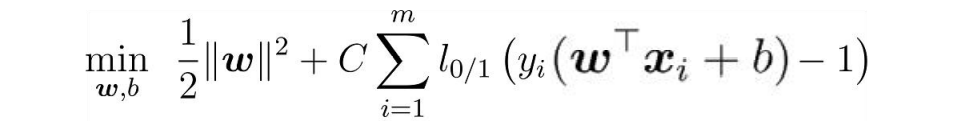
在这里插入图片描述
其中C>0为惩罚参数
在这里插入图片描述
然而损失函数有着一定的缺陷：非凸、非连续, 不易优化，因此用替代损失函数。
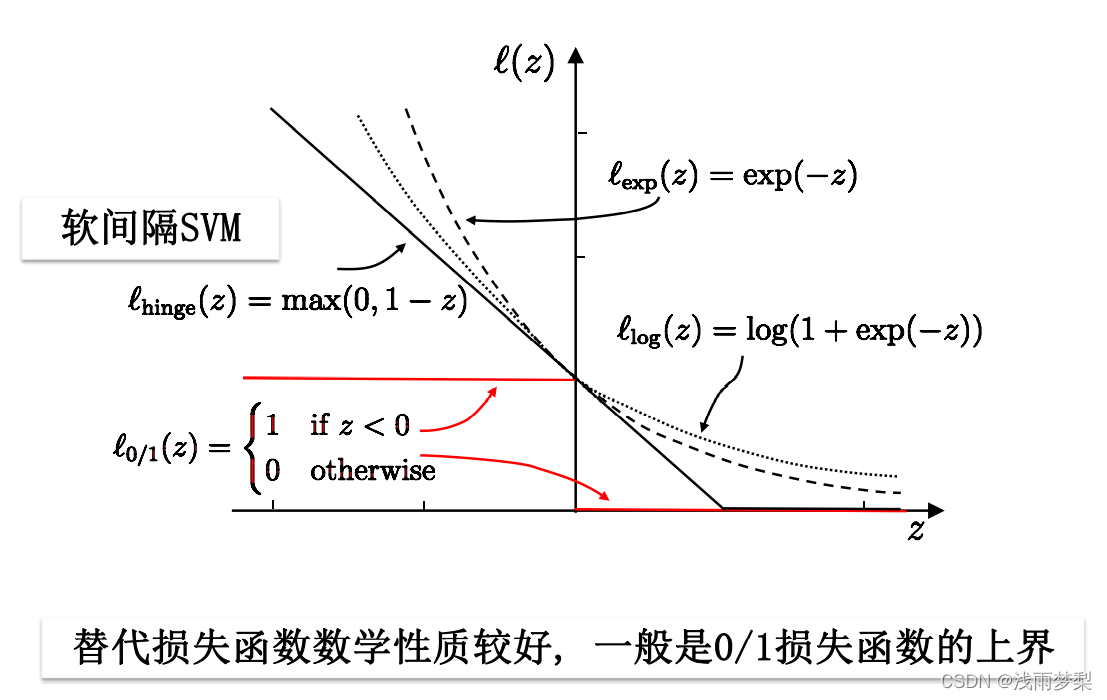
在这里插入图片描述

2.4 支持向量回归

支持向量回归允许模型输出和实际输出间存在2ε的偏差
在这里插入图片描述
其中，ε为松弛变量，反映了对野点的容忍程度
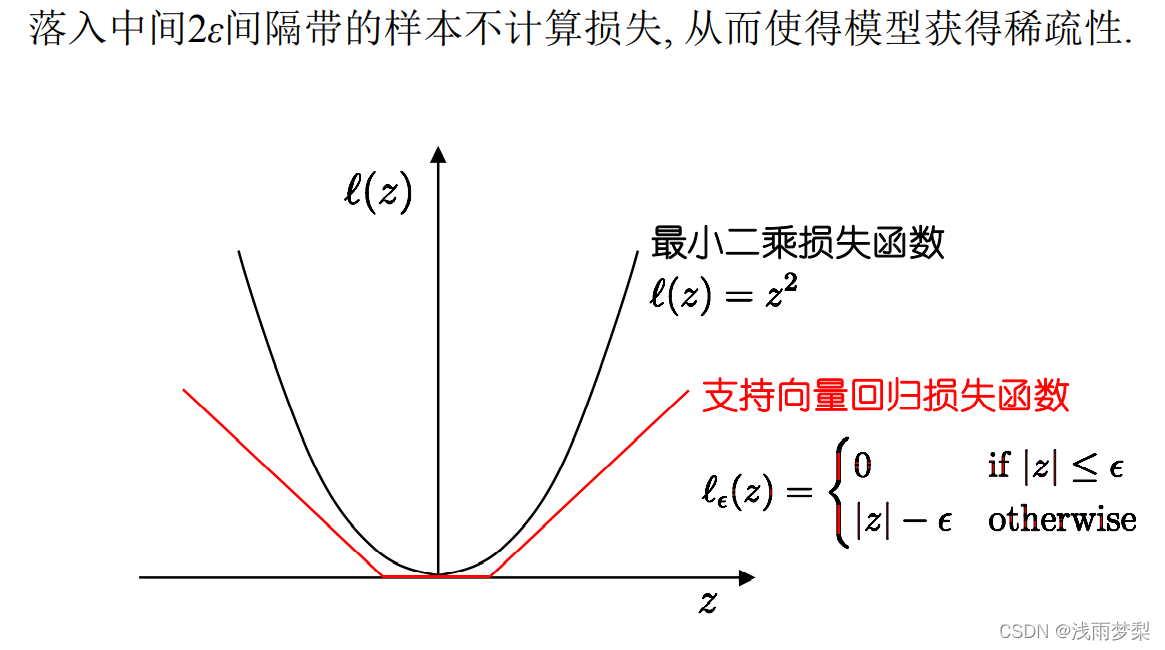
在这里插入图片描述
于是求解变成了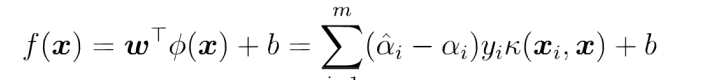：在这里插入图片描述

三、代码实战

3.1 数据准备

选择随机生成的数据集， 用make_hastie-10-2生成。有十个维度，标签是两种，因此做二分类。随机生成一千条数据，80%做训练，20%做测试

data, label = datasets.make_hastie_10_2(n_samples=1000)
x_train, x_test, y_train, y_test = train_test_split(data, label, test_size=0.2)

3.2 算法实现

数据结构

class optStruct:
    """
	数据结构，维护所有需要操作的值
	Parameters：
		dataMatIn - 数据矩阵
		classLabels - 数据标签
		C - 松弛变量
		toler - 容错率
		kTup - 包含核函数信息的元组,第一个参数存放核函数类别，第二个参数存放必要的核函数需要用到的参数
	"""

    def __init__(self, dataMatIn, classLabels, C, toler, kTup):
        self.X = dataMatIn  # 数据矩阵
        self.labelMat = classLabels  # 数据标签
        self.C = C  # 松弛变量  -> 对野点的容忍程度
        self.tol = toler  # 容错率
        self.m = np.shape(dataMatIn)[0]  # 数据矩阵行数
        self.alphas = np.mat(np.zeros((self.m, 1)))  # 根据矩阵行数初始化alpha参数为0
        self.b = 0  # 初始化b参数为0
        self.eCache = np.mat(np.zeros((self.m, 2)))  # 根据矩阵行数初始化虎误差缓存，第一列为是否有效的标志位，第二列为实际的误差E的值。
        self.K = np.mat(np.zeros((self.m, self.m)))  # 初始化核K
        for i in range(self.m):  # 计算所有数据的核K
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)

计算核函数，通过核函数将数据转换更高维的空间

def kernelTrans(X, A, kTup):
    
    m, n = np.shape(X)
    K = np.mat(np.zeros((m, 1)))
    if kTup[0] == 'lin':
        K = X * A.T  # 线性核函数,只进行内积。
    elif kTup[0] == 'rbf':  # 高斯核函数,根据高斯核函数公式进行计算
        for j in range(m):
            deltaRow = X[j, :] - A
            K[j] = deltaRow * deltaRow.T
        K = np.exp(K / (-1 * kTup[1] ** 2))  # 计算高斯核K
    else:
        raise NameError('核函数无法识别')
    return K  # 返回计算的核K

smo算法

def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=('lin', 0)):
    
    oS = optStruct(np.mat(dataMatIn), np.mat(classLabels).transpose(), C, toler, kTup)  # 初始化数据结构
    iter = 0  # 初始化当前迭代次数
    entireSet = True
    alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):  # 遍历整个数据集都alpha也没有更新或者超过最大迭代次数,则退出循环
        alphaPairsChanged = 0
        if entireSet:  # 遍历整个数据集
            for i in range(oS.m):
                alphaPairsChanged += innerL(i, oS)  # 使用优化的SMO算法
                print("全样本遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        else:  # 遍历非边界值
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]  # 遍历不在边界0和C的alpha
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i, oS)
                print("非边界遍历:第%d次迭代 样本:%d, alpha优化次数:%d" % (iter, i, alphaPairsChanged))
            iter += 1
        if entireSet:  # 遍历一次后改为非边界遍历
            entireSet = False
        elif (alphaPairsChanged == 0):  # 如果alpha没有更新,计算全样本遍历
            entireSet = True
        print("迭代次数: %d" % iter)
    return oS.b, oS.alphas  # 返回SMO算法计算的b和alphas

优化的smo算法

def innerL(i, oS):
    
    # 步骤1：计算误差Ei
    Ei = calcEk(oS, i)
    # 优化alpha,设定一定的容错率。
    if ((oS.labelMat[i] * Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or (
            (oS.labelMat[i] * Ei > oS.tol) and (oS.alphas[i] > 0)):
        # 使用内循环启发方式2选择alpha_j,并计算Ej
        j, Ej = selectJ(i, oS, Ei)
        # 保存更新前的aplpha值，使用深拷贝
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        # 步骤2：计算上下界L和H
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L == H:
            print("L==H")
            return 0
        # 步骤3：计算eta
        eta = 2.0 * oS.K[i, j] - oS.K[i, i] - oS.K[j, j]
        if eta >= 0:
            print("eta>=0")
            return 0
        # 步骤4：更新alpha_j
        oS.alphas[j] -= oS.labelMat[j] * (Ei - Ej) / eta
        # 步骤5：修剪alpha_j
        oS.alphas[j] = clipAlpha(oS.alphas[j], H, L)
        # 更新Ej至误差缓存
        updateEk(oS, j)
        if (abs(oS.alphas[j] - alphaJold) < 0.00001):
            print("alpha_j变化太小")
            return 0
        # 步骤6：更新alpha_i
        oS.alphas[i] += oS.labelMat[j] * oS.labelMat[i] * (alphaJold - oS.alphas[j])
        # 更新Ei至误差缓存
        updateEk(oS, i)
        # 步骤7：更新b_1和b_2
        b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.K[i, j]
        b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (
                oS.alphas[j] - alphaJold) * oS.K[j, j]
        # 步骤8：根据b_1和b_2更新b
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]):
            oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]):
            oS.b = b2
        else:
            oS.b = (b1 + b2) / 2.0
        return 1
    else:
        return 0

计算误差

def calcEk(oS, k):
   
    fXk = float(np.multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

内循环启发方式计算Ej

def selectJ(i, oS, Ei):
    
    maxK = -1
    maxDeltaE = 0
    Ej = 0  # 初始化
    oS.eCache[i] = [1, Ei]  # 根据Ei更新误差缓存
    validEcacheList = np.nonzero(oS.eCache[:, 0].A)[0]  # 返回误差不为0的数据的索引值
    if (len(validEcacheList)) > 1:  # 有不为0的误差
        for k in validEcacheList:  # 遍历,找到最大的Ek
            if k == i: continue  # 不计算i,浪费时间
            Ek = calcEk(oS, k)  # 计算Ek
            deltaE = abs(Ei - Ek)  # 计算|Ei-Ek|
            if (deltaE > maxDeltaE):  # 找到maxDeltaE
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej  # 返回maxK,Ej
    else:  # 没有不为0的误差
        j = selectJrand(i, oS.m)  # 随机选择alpha_j的索引值
        Ej = calcEk(oS, j)  # 计算Ej
    return j, Ej  # j,Ej

修剪alpha_j

def clipAlpha(aj, H, L):
    
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

更新Ej至误差缓存

def updateEk(oS, k):
    """
	计算Ek,并更新误差缓存
	Parameters：
		oS - 数据结构
		k - 标号为k的数据的索引值
	Returns:
		无
	"""
    Ek = calcEk(oS, k)  # 计算Ek
    oS.eCache[k] = [1, Ek]  # 更新误差缓存

可视化样本标签

def showDataSet(dataMat, labelMat):
    # 正样本
    data_plus = []
    # 负样本
    data_minus = []
    for i in range(len(dataMat)):
        if labelMat[i] > 0:
            data_plus.append(dataMat[i])
        else:
            data_minus.append(dataMat[i])
    # 转换为numpy矩阵
    data_plus_np = np.array(data_plus)
    # 转换为numpy矩阵
    data_minus_np = np.array(data_minus)
    # 正样本散点图（scatter）
    # transpose转置
    plt.scatter(np.transpose(data_plus_np)[0], np.transpose(data_plus_np)[1])
    # 负样本散点图（scatter）
    plt.scatter(np.transpose(data_minus_np)[0], np.transpose(data_minus_np)[1])
    # 显示
    plt.show()

3.3 运行结果及分析

样本分类可视化：

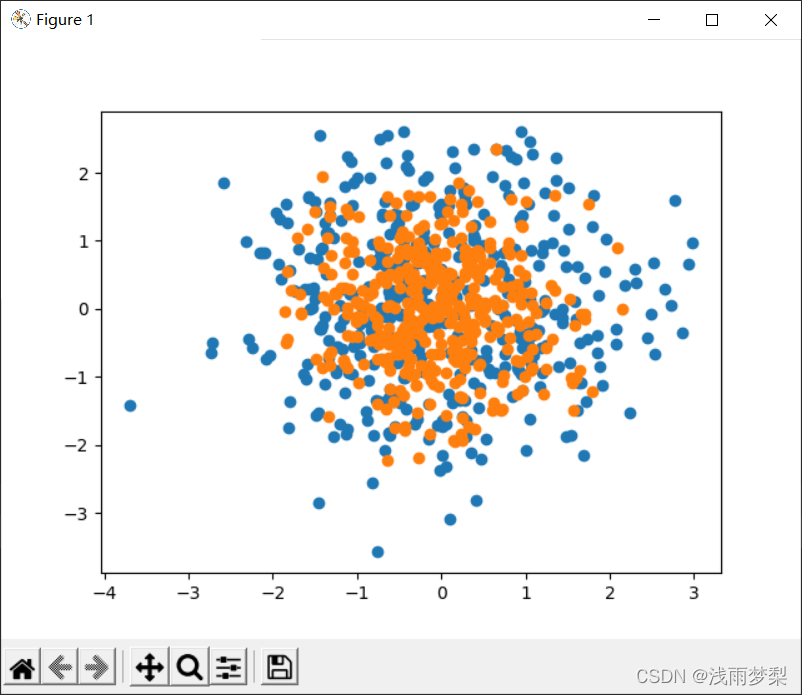
在这里插入图片描述
运行结果：
在这里插入图片描述
数据集采用随机生成的方式能很好的运行svm并且有较高的正确率

四、总结

SVM从原理到代码实现难度都挺大，现在还是没怎么吃透，以后还需加强它的学习。

浅雨梦梨
关注
  • 21
    点赞
  • 踩
  • 64
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
【机器学习详解】SVM解二分类,多分类,及后验概率输出
dujiahaogod的博客
04-09 5959
支持向量机(Support Vector Machine)曾经在分类、回归问题中非常流行。支持向量机也称为最大间隔分类器，通过分离超平面把原始样本集划分成两部分。 首先考虑最简单的情况：线性可分支持向量机，即存在一个超平面可以把训练样本分开。 1.线性可分支持向量机 1.考虑一个线性二分类的问题；如下左图，在二维平面上有两种样本点x，目标值分别标记为{-1,1}，可以作出无数条直线wTx+b...
SVM二分类的MATLAB实现
07-12
是基于课程SVM原理内容写的SVM的底层实现，包括线性的和非线性采用核函数的。初学者，比较。。。
SVM 用于将数据分类为两分类或多分类（Matlab代码实现）
weixin_46039719的博客
12-04 5886
本文旨在帮助可视化学习的分类器，在训练非线性 C-SVM 以将二维数据（2 个特征）分类为 2 个或更多类时。C = Inf 给出硬边距分类器，而 C < Inf 给出 1 范数软边距分类器的情况。MATLAB 的 quadprog 用于求解对偶变量 a。求解器设置为使用内点方法。高斯径向基函数 （RBF） 核用于生成非线性边界。在二进制分类文件 （SVMtrial.m） 中：有 6 个不同的训练集可供使用。输出是分类器的 3D 网格图和支持向量的数量。二元分类的数据集：（1） 典型。
机器学习(23) SVM 示例4:【Python】解决二分类(示例1、2、3)
luyouqi11的博客
08-08 1392
z = svc.predict(np.c_[x.flatten(),y.flatten()])#因为predict中是要输入一个二维的数据，因此需要展开。z = svc.predict(np.c_[x.flatten(),y.flatten()])#因为predict中是要输入一个二维的数据，因此需要展开。print(f'预测样本数据X的对数概率 svc.predict_log_proba(X) ={svc1.predict_log_proba(X)}'),10的0次幂,10,1000,10000。
使用Python实现SVM来解决二分类问题
m0_73916791的博客
11-28 1108
请确保在运行代码之前安装所需的库（如scikit-learn和Matplotlib）。此代码可根据实际问题进行调整和扩展。然后，我们使用训练好的模型在测试集上进行预测，并将预测结果保存在。最后，我们使用Matplotlib库绘制数据点和分隔超平面。函数将数据集拆分为训练集和测试集。函数生成一个包含两个类别的二分类数据集。函数用于绘制数据点，不同类别的点使用不同的颜色表示。函数绘制分隔超平面。方法用于计算分隔超平面，然后使用。属性绘制了支持向量的圆圈表示。对象作为SVM模型，并使用。在此示例中，我们使用。
SVM的二分类问题（fitcsvm）
热门推荐
aixuexidelele的博客
11-12 1万+
Mａｔｌａｂ实现ｆｉｔｃｓｖｍ基于支持向量机SVM的二分类问题（fitcsvm函数）线性二分类代码实现实验结果非线性二分类代码实现实验结果注 基于支持向量机SVM的二分类问题（fitcsvm函数） matlab2018及之后的版本取消了svmtrain和svmclassify函数，取而代之的更多的fitcsvm和predict函数。但是也使得决策边界无法直接生成，需要根据fitcsvm中得到的参数画出决策边界。 线性二分类 问题1：编写程序，用SVM方法解决线性二分类问题 数据集：testSet-linea
傻子都能看懂的SVM
qq_37633207的博客
10-24 1131
文章目录SVM简介物理世界角度理解svm知识前提0-数学基本知识1-几何间隔与函数间隔2-拉格朗日乘子法与KKT条件如何理解拉格朗日乘子法什么是负梯度为什么λ\lambdaλ要大于0？3-拉格朗日对偶问题对偶问题的性质什么是对偶空间如何求解一个线性规划的对偶问题？2-SVM 目标函数与约束的推导数据集如何去除优化公式中的绝对值为优化函数添加约束项进一步化简复杂的优化目标如何求解优化函数？求解min⁡w,bL(w,b,α)\min \limits_{w,b}L(w,b,\alpha)w,bmin​L(w,b,
SVM做二分类与多分类尝试
magicboom的博客
04-02 8339
利用 SVM( Support Vector Machine) 做分类是机器学习比较成熟的算法。 关于SVM, 我有一篇博文已经详细的介绍了其原理： 传送门： SVM 原理简述 今天，我们利用Python 的OpenCV中的ML模块进行SVM 而分类的演练。 首先是Binary Classification. __author__ = "Luke Liu" #encoding="u...
用svm对数据进行二分类（完整代码）
bookshu6的博客
12-26 1万+
一、前言 这是笔者学习opencv中svm的一个小例子，数据集是用sk-learn库中的函数生成的。功能就是对该数据进行二分类。 为了学习的更深入，笔者将svm常用的四种核，linear，inter，sigmoid，rbf作了对比。 详细步骤见代码 二、代码 import numpy as np from cv2 import cv2 from sklearn import datasets import matplotlib.pyplot as plt from sklearn import model_
SVM实现多分类的三种方案
weixin_30547797的博客
03-11 489
SVM本身是一个二值分类器 　　SVM算法最初是为二值分类问题设计的，当处理多类问题时，就需要构造合适的多类分类器。 　　目前，构造SVM多类分类器的方法主要有两类 　　（1）直接法，直接在目标函数上进行修改，将多个分类面的参数求解合并到一个最优化问题中，通过求解该最优化问题“一次性”实现多类分类。这种方法看似简单，但其计算复杂度比较高，实现起来比较困难，只适合用于小型问题中； 　　（2）...
机器学习之-svm学习课件
10-22
机器学习之svm学习课件 机器学习之svm学习课件 机器学习之svm学习课件
机器学习算法之SVM算法实现.zip
最新发布
04-20
机器学习算法 机器学习算法之SVM算法实现
基于传统机器学习方法SVM对kaggle猫狗图片分类
11-09
2、本项目适合计算机相关专业(如计科、人工智能、通信工程、自动化、电子信息等)的在校学生、老师或者企业员工下载学习，也适合小白学习进阶，当然也可作为毕设项目、课程设计、作业、项目初期立项演示等。...
机器学习之svm
01-04
svm 向量机 机器学习 svm 向量机 机器学习 svm 向量机 机器学习 svm 向量机 机器学习
5_roc_SVM分类_机器学习_
09-29
用from sklearn.datasets import make_circles
高光谱遥感影像分类，机器学习分类，SVM算法，Salinas数据集
03-10
是用于高光谱遥感影像分类的机器学习脚本，其中使用了支持向量机算法（Support Vector Machine，SVM）对Salinas数据集进行分类。 SVM算法是一种基于统计学习理论的分类算法，其通过在高维空间中寻找一个超平面，将...
机器学习——SVM，微博不实信息分类
06-24
利用支持向量机对于微博爬取的不实信息进行分类，并且爬取正常的微博信息，判断微博是否不实。其中正常微博为0，不实微博为1
机器学习-SVM分类源码
12-03
借助OPENCV,使用机器学习方法，实现手写字分类识别；提供图片，及所有源码，opencv版本3.3.0
改进的svm二分类算法
09-03
改进的SVM二分类算法有很多种，以下列举几种常见的改进方法： 1. 多核学习（MKL）：传统的SVM算法使用单一核函数进行特征转换，而MKL算法可以学习多个核函数的权重，从而更灵活地将不同核函数的特性结合起来，提升分类性能。 2. 核函数选择：传统的SVM算法使用常见的核函数（如线性核、多项式核、高斯核等），而改进的方法可以根据具体问题选择更适合的核函数，例如径向基函数（RBF）核函数的带宽选择方法。 3. 样本权重调整：在标准SVM中，对于每个样本，其权重都是相等的。但是对于不平衡数据集，可以通过调整样本的权重，使得少数类样本具有更大的权重，从而提升分类器对少数类的识别能力。 4. 多分类扩展：SVM原本是二分类算法，但可以通过一些扩展方法将其应用于多分类问题，例如一对一（OvO）和一对多（OvR）策略等。 5. 增量式学习：传统的SVM算法需要重新训练整个模型，无法直接适应新加入的样本。改进的方法可以通过增量学习的方式，实现模型的在线更新，并且避免重复训练的开销。 这些是常见的改进方法，针对具体问题的不同，还有其他更多的改进技术可供选择。希望以上信息能对您有所帮助！

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值