前言
最近重拾高数的时候给博主整自闭了,什么极限啊、积分啊博主忘的是干干净净。
属实是应了那句 『课上学到的东西在下课的一瞬间就全部还给了老师』。

吐槽过后就要开始想办法补救。
就在博主薅着所剩无几的头发,苦苦思索的时候,我突然想起来我亲爱的哥哥(人生导师)之前跟我提到过的一个软件——Wolfram Mathematica 11。
不过当时我才高中毕业,那时候他还在准备考研(现在已经上岸了,老哥NB)。他当时跟我说了一堆东西,年轻气盛的我属实是啥也没记住,只留下了一些模糊的印象以及电脑上一堆奇奇怪怪的软件。而在这些软件之中,Wolfram Mathematica 11给我的印象是最深刻的。
还记得那是一个寒冷的冬日,哈尔滨的冬天总是那么的单刀直入,让人恨不得和暖气片绑在一起共度余生。当时的博主还是一个青涩的大一新生,那天正坐在一间教室里孤独地做着高数作业。
由于博主一直以来都不是很擅长数学这类抽象的学科,很快的我就卡在了一道题上动弹不得(好像是积分,又好像是求极限)。
博主属于那种死脑筋爱钻牛角尖的人,认真起来连自己都不放过,于是乎博主迅速的把题发给了万能的哥哥,请求他的帮助。他看到消息之后大概只用了1~2分钟,返回给我一个截图。
截图找不到了,但内容就是那道题的答案,使用的软件就是Wolfram Mathematica 11。
从那之后博主就一直惦记着这个神奇的软件,心里留存着『无论如何也得把这绝世软件学一学』的想法。
今天正式开坑『Wolfram Mathematica 11的学习笔记』,不定时更新。
由于博主并没有抱着十分专业的心态来入坑,所以文章内容基本上就是博主在使用 Wolfram Mathematica 11 的过程中学习到的一些函数的介绍。如果想要了解更加深入的使用知识以及软件的使用技巧的话,菜狗博主建议另寻大佬。
前置介绍
- 软件名称:Wolfram Mathematica 11
- 学习参考资料(视频):Mathematica 11.0教程
- 学习参考视频(网站):Wolfram 语言与系统参考资料中心
Expand(公式展开)
一.函数形式
Expand[expr]:将公式expr中所有的乘积与正整数幂进行展开
Expand[expr,patt]:只将公式expr中包含patt形式的部分进行展开
二.演示
①将公式 h 2 ( v x + v y ) 2 h^2(vx+vy)^2 h2(vx+vy)2进行展开。
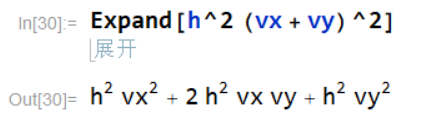
②将公式 h 2 ( v x + v y ∗ ( 3 x + 4 y ) 2 ) − 8 h^2 (vx + vy*(3 x + 4 y)^2)^{-8} h2(vx+vy∗(3x+4y)2)−8进行展开。
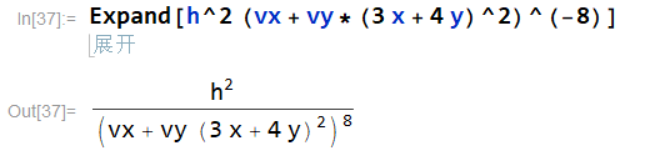
③将公式 h 2 ( x + ( y + x ) 2 ) 7 4 h^2 (x + (y + x)^2)^{\frac{7}{4}} h2(x+(y+x)2)47进行展开。
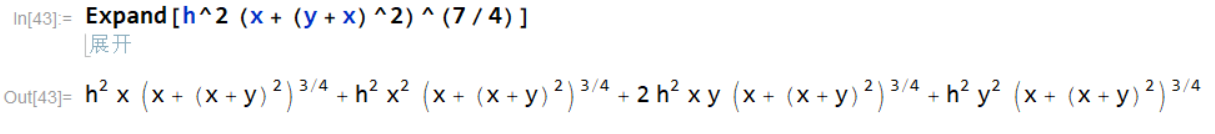
根据②③我们会发现:
- ( v x + v y ∗ ( 3 x + 4 y ) 2 ) − 8 (vx + vy*(3 x + 4 y)^2)^{-8} (vx+vy∗(3x+4y)2)−8中只有 − 1 -1 −1次方被展开,成为了 1 ( v x + v y ∗ ( 3 x + 4 y ) 2 ) 8 \frac{1}{(vx + vy*(3 x + 4 y)^2)^{8}} (vx+vy∗(3x+4y)2)81,而其中的 ( 3 x + 4 y ) 2 (3 x + 4 y)^2 (3x+4y)2还有整体的8次方都没有被展开;
- ( x + ( y + x ) 2 ) 7 4 (x + (y + x)^2)^{\frac{7}{4}} (x+(y+x)2)47中只有 ( x + ( y + x ) 2 ) 1 (x + (y + x)^2)^1 (x+(y+x)2)1被展开,成为了 x + x 2 + 2 x y + y 2 x + x^2 + 2 x y + y^2 x+x2+2xy+y2,而剩下的 ( x + ( y + x ) 2 ) 3 4 (x + (y + x)^2)^{\frac{3}{4}} (x+(y+x)2)43以及其内部的 ( y + x ) 2 (y+x)^2 (y+x)2没有被展开;
所以博主觉得,对于将公式expr中所有的乘积与正整数幂进行展开的正确解读应该是
- 如果公式expr中存在正实数次幂,则会将该实数的整数部分分离出来,然后将整数幂项进行展开,
例如 ( x + ( y + x ) 2 ) 7 4 (x + (y + x)^2)^{\frac{7}{4}} (x+(y+x)2)47分离成 ( x + ( y + x ) 2 ) ∗ ( x + ( y + x ) 2 ) 3 4 (x + (y + x)^2)*(x + (y + x)^2)^{\frac{3}{4}} (x+(y+x)2)∗(x+(y+x)2)43); - 如果公式expr中存在负数次幂,则只将-1次幂展开,剩下的部分保留不做处理;
- 如果展开停止在括号外部,则括号内部的公式不会展开,
例如③中 ( x + ( y + x ) 2 ) 3 4 (x + (y + x)^2)^{\frac{3}{4}} (x+(y+x)2)43的展开停止在了外层, ( y + x ) 2 (y+x)^2 (y+x)2无法展开;
④将公式 6 ( x + 1 ) + ( y + 1 ) 2 + ( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 6 (x + 1) + (y + 1)^2 + ((y + 1)^2 + (x + 1)^2)^2 6(x+1)+(y+1)2+((y+1)2+(x+1)2)2中所有包含 ( y + 1 ) (y+1) (y+1)的部分进行展开。
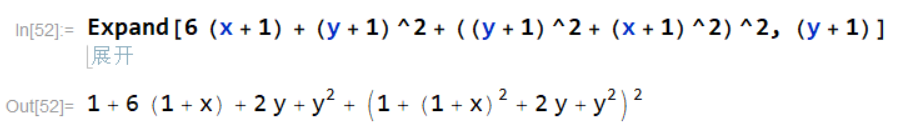
⑤将公式 6 ( x + 1 ) + ( y + 1 ) 2 + ( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 6 (x + 1) + (y + 1)^2 + ((y + 1)^2 + (x + 1)^2)^2 6(x+1)+(y+1)2+((y+1)2+(x+1)2)2中所有包含 ( y + 1 ) 2 (y+1)^2 (y+1)2的部分进行展开。
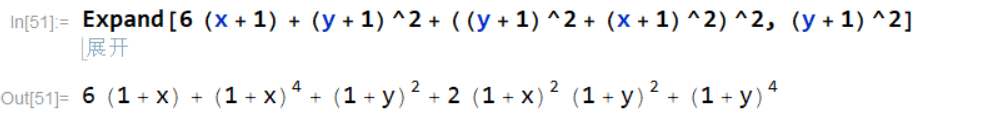
这里④与⑤产生了差别,我们分析一下:
- 在④中我们只将包含
(
y
+
1
)
(y+1)
(y+1)的部分进行展开。
在 ( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 ((y + 1)^2 + (x + 1)^2)^2 ((y+1)2+(x+1)2)2中 ( y + 1 ) 2 (y+1)^2 (y+1)2包含 ( y + 1 ) (y+1) (y+1),所以被展开;
但 ( x + 1 ) 2 (x + 1)^2 (x+1)2不包含 ( y + 1 ) (y+1) (y+1),所以没有被展开;
( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 ((y + 1)^2 + (x + 1)^2)^2 ((y+1)2+(x+1)2)2整体在某种意义上也是包含 ( y + 1 ) (y + 1) (y+1)的,但没有展开; - 在⑤中我们只将包含
(
y
+
1
)
2
(y+1)^2
(y+1)2的部分进行展开。
在 ( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 ((y + 1)^2 + (x + 1)^2)^2 ((y+1)2+(x+1)2)2中 ( y + 1 ) 2 (y+1)^2 (y+1)2包含 ( y + 1 ) 2 (y+1)^2 (y+1)2,但没有展开;
( x + 1 ) 2 (x + 1)^2 (x+1)2不包含 ( y + 1 ) 2 (y+1)^2 (y+1)2,所以没有被展开;
( ( y + 1 ) 2 + ( x + 1 ) 2 ) 2 ((y + 1)^2 + (x + 1)^2)^2 ((y+1)2+(x+1)2)2整体包含 ( y + 1 ) 2 (y + 1)^2 (y+1)2,被展开;
根据这些,博主推断只将公式expr中包含patt形式的部分进行展开的意思为:将公式中所有的patt用一个新变量表示,只对 完全包含patt 的部分进行展开。
那什么是完全包含?
在函数
f
(
x
)
=
[
(
y
+
1
)
+
(
x
+
1
)
2
]
2
f(x)=[(y+1)+(x+1)^2]^2
f(x)=[(y+1)+(x+1)2]2中,
f
(
x
)
f(x)
f(x)完全包含
(
y
+
1
)
(y+1)
(y+1),所以
f
(
x
)
f(x)
f(x)会被全部展开,但
(
x
+
1
)
2
(x+1)^2
(x+1)2并不会被展开:
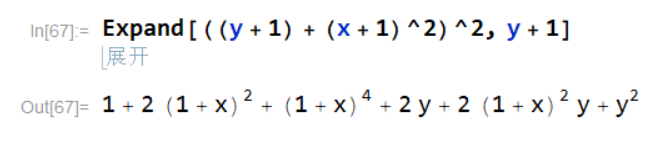
而在函数
f
(
x
)
=
[
(
y
+
1
)
2
+
(
x
+
1
)
2
]
2
f(x)=[(y+1)^2+(x+1)^2]^2
f(x)=[(y+1)2+(x+1)2]2中,
(
y
+
1
)
2
(y+1)^2
(y+1)2完全包含
(
y
+
1
)
(y+1)
(y+1),但
f
(
x
)
f(x)
f(x)只是包含了
(
y
+
1
)
(y+1)
(y+1),并不完全包含(可以理解成不在同一层)。所以
(
y
+
1
)
2
(y+1)^2
(y+1)2会被完全展开,而
f
(
x
)
f(x)
f(x)不会:
N(实数化)
一.函数形式
N[x]:将x转化为实数
N[x,n]:将x转化为实数,并尝试性地保留n位精度
二.演示
①将1转化为实数。

②将0转化为实数。

③将 2 31 2^{31} 231转化为实数。
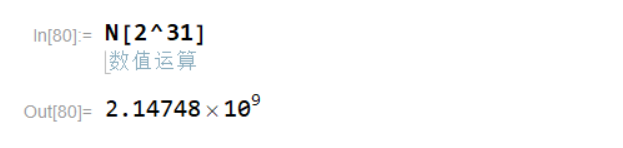
④将0123转化为实数。

⑤将1/3转化为实数。

通过上述试验以及博主自己做的一些测试来说,目前博主得到的结论是:
- N [ x ] N[x] N[x]会保留x的6位有效数字,如果x不足6位则不做处理(不会补0),例如①②;
- 如果x的整数位超过6位(等于6位也算),则会转变成科学计数法,例如③;
- 若x为分数形式,则会先把x化成实数再取6位有效数字,例如⑤;
- N [ x ] N[x] N[x]在计算时会先清除前导0与后缀无效0(例如1.000),例如④
⑥将 2 32 2^{32} 232化为实数,并尝试性地保留10位精度。
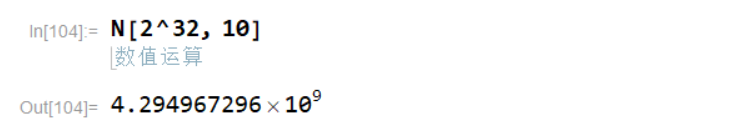
⑦将 0.1 0.1 0.1化为实数,并尝试性地保留5位精度。

⑧将 123456789.987654321 123456789.987654321 123456789.987654321实数化,并尝试性地保留10位精度。

关于
N
[
x
,
n
]
N[x,n]
N[x,n],一开始我以为是保留n个有效数字,但被
N
[
0.1
,
5
]
N[0.1,5]
N[0.1,5]打脸了。
测了半天,博主觉得
N
[
x
,
n
]
N[x,n]
N[x,n]应该是:
- 如果x不是实数形式/整数形式,则会将x算出来,保留其n位有效数字,缺位小数点后补0;
- 否则就先计算出 N [ x ] N[x] N[x]的值,查看 N [ x ] N[x] N[x]是否到达 n n n位;
- 如果 N [ x ] N[x] N[x]不够n位,则 N [ x , n ] = = N [ x ] N[x,n]==N[x] N[x,n]==N[x];
- 如果 N [ x ] N[x] N[x]为科学计数法,则将a*10e中的a进行处理,保留其n位有效数字,缺位小数点后补0;
- 否则就按正常的处理方式,保留n位有效数字,缺位小数点后补0;
对于N[12345.123456,10],N[12345.123456]=12345.1,而12345.1不足10位,所以N[12345.123456,10]=N[12345.123456]=12345.1。

可能是博主自己比较喜欢钻牛角的缘故,像这样的篇幅,正常的博主至少也可以介绍5个函数,而菜狗博主只能写2个。没办法,测试的时候总会出现新的花样,再加上博主在遇到这种神奇的东西的时候总是想试图搞清其内部的逻辑,导致内容会非常的( ) ( )。
博主只是一个萌新,如果内容有哪些不对的地方还请巨巨们指教。
今天就先到这,我们改日再见。
(实际上还想再写两个,但是博主是懒狗(●’◡’●))






















 1217
1217











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








