实验6 图的应用

最新推荐文章于 2022-05-29 16:42:39 发布

原创最新推荐文章于 2022-05-29 16:42:39 发布 · 733 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #数据结构

数据结构专栏收录该内容

8 篇文章

订阅专栏

本文介绍了如何使用图的抽象数据类型（ADT）来解决一个军事信息传递网络的问题。网络由多个部门组成，信息只能单向传递，通过深度优先搜索（DFS）确定部门间的信息可达性。算法读取输入的边信息构建邻接矩阵，然后遍历寻找能传递至所有部门的节点数量。示例中展示了算法的运行过程，并分析了其时间和空间复杂度。

实验六图的应用

[问题描述]
应用图的ADT的物理实现来解决图的应用问题。
　某国的军队由N个部门组成，为了提高安全性，部门之间建立了M条通路，每条通路只能单向传递信息，即一条从部门a到部门b的通路只能由a向b传递信息。信息可以通过中转的方式进行传递，即如果a能将信息传递到b，b又能将信息传递到c，则a能将信息传递到c。一条信息可能通过多次中转最终到达目的地。
　　由于保密工作做得很好，并不是所有部门之间都互相知道彼此的存在。只有当两个部门之间可以直接或间接传递信息时，他们才彼此知道对方的存在。部门之间不会把自己知道哪些部门告诉其他部门。
　
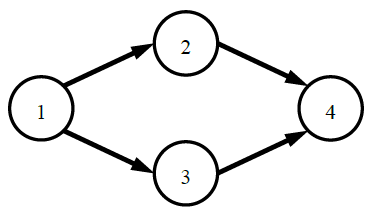
上图中给了一个4个部门的例子，图中的单向边表示通路。部门1可以将消息发送给所有部门，部门4可以接收所有部门的消息，所以部门1和部门4知道所有其他部门的存在。部门2和部门3之间没有任何方式可以发送消息，所以部门2和部门3互相不知道彼此的存在。
　　现在请问，有多少个部门知道所有N个部门的存在。或者说，有多少个部门所知道的部门数量（包括自己）正好是N。
[输入形式]
输入的第一行包含两个整数N, M，分别表示部门的数量和单向通路的数量。所有部门从1到N标号。
　　接下来M行，每行两个整数a, b，表示部门a到部门b有一条单向通路。
[输出形式]
　输出一行，包含一个整数，表示答案。

一、问题分析

要处理的对象（数据）:
从键盘键入的一组有向图的边存储的数据所代表的整数。
要实现的功能：
将所有边的信息读取完成后，输出能通往所有顶点的顶点数和所有顶点都能汇总到的顶点数之和。
处理后的结果如何显示：
将计算好符合条件的顶点数输出到屏幕。

二、数据结构和算法设计

1.抽象数据类型设计

【图ADT的表示】
ADT IntegerSet{
	数据对象:一组有向图的边存储的数据所代表的整数
	数据关系:输入的整数满足有向图中的顶点关系，可以用图的ADT实现。
	基本操作：
    Graph() {} // 默认构造函数	
	virtual void Init(int n) = 0;//初始化一个有n个顶点的图	
	virtual int n() = 0;//返回顶点的数量
	virtual int e() = 0;//返回边的数量
	virtual int first(int v) =0;// 返回v的第一个邻居 
	virtual int next(int v, int w) =0;// 返回v的下一个邻居	 
	virtual int locateVex(char u) = 0;//找到(包含实际信息的）顶点在图中的位置
	virtual int getVex(int v) = 0;//返回某个顶点的值(实际信息) 	
	virtual void putVex(int v, int value) = 0;//给某个顶点赋值
	virtual void setEdge(int v1, int v2, int wght) = 0;	//设置边的权重	
	virtual int weight(int v1, int v2) = 0;// Return:边i、j或0的权值
	virtual int getMark(int v) =0;//获取顶点的标记值
	virtual void setMark(int v, int val) =0;//设置顶点的标记值
}

2.物理数据对象设计

物理存储方式：
由于使用图的邻接矩阵实现，采用二维指针实现整型的存储，将边和顶点的信息存储在计算机中。

3.算法思想的设计：

通过循环读取屏幕中输入的每一条边来构造一个邻接矩阵，然后利用循环对n个顶点分别进行一次深度优先搜索，用另一个二维数组记录下与该顶点有联系的点(也就是DFS可以到的点)，比如顶点s和顶点e有联系(正向DFS可以到达的)，那么顶点e和顶点s就也有联系(反向DFS可以到达的)，则利用二维数组对应邻接矩阵边的位置上分别标记他们的联系为1，无关系则为初始值0，最后利用两次循环统计一下每个顶点(包括自己)相关联的点的个数，如果有n个，则能通往所有顶点的顶点数和所有边数都能汇总到的顶点数的计数器加1，循环结束后输出计数器所记录的值。

4.样例求解过程：

样例输入：
4 4
1 2
1 3
2 4
3 4
用邻接矩阵构造图：
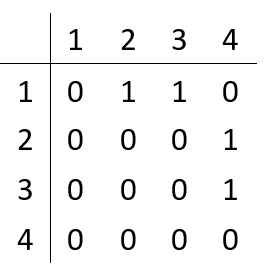
在这里插入图片描述
开始利用循环对每一个顶点进行DFS，并记录顶点之间的关系：
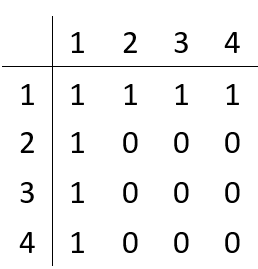
a.对1进行DFS，并改变二维数组元素的值：
DFS结果：1-2-4-3
二维数组元素改变：

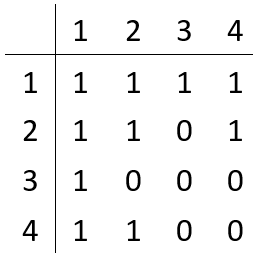
b.对2进行DFS，并改变二维数组元素的值：
DFS结果：2-4
二维数组元素改变：
在这里插入图片描述
c.对1进行DFS，并改变二维数组元素的值：
DFS结果：3-4
二维数组元素改变：

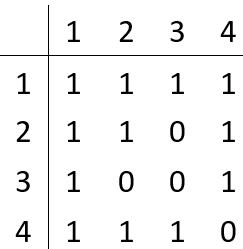
d.对1进行DFS，并改变二维数组元素的值：
DFS结果：4
二维数组元素改变：

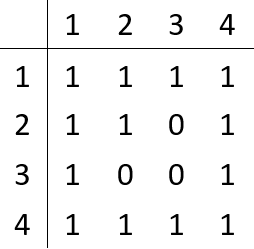
统计每个顶点与其他顶点关系，发现1与4都与其他顶点存在关系，计数器为2，输出能通往所有顶点的顶点数和所有顶点都能汇总到的顶点数之和为2

5.关键功能的算法步骤：

【构造邻接矩阵】

//将输入代表有向边的两个整数s1,s2在邻接矩阵中对应的元素位置找出，利用基本操作将边的权值置为1
G1->setEdge(G1->locateVex(s1), G1->locateVex(s2), 1);

【DFS算法将二维数组进行改变】

//传入该图和有关系的两个顶点
void DFS(Graph *G,int v,int s)
{
    //DFS算法标记遍历过该顶点
   	G->setMark(v,1);
    //有关系的两个顶点在二维数组上标记
   	du[v+1][s+1]=du[s+1][v+1]=1;
    //DFS算法进入下一条未被访问过的顶点
    for(int w=G->first(v);w<G->n();w=G->next(v,w))
        if(G->getMark(w)==0&&G->weight(v, w)!=0)//没被访问过且存在边(w,v)
            DFS(G,w,s);
}

【计数器通过循环计数】

for(int i=1;i<=n;i++){//双重循环
		int j;
		for(j=1;j<=n;j++){
			if(du[i][j]==0) break;
		}
		if(j==n+1) cmp++;//如果该顶点与每个顶点都有关系，则计数器加1
}

三、算法性能分析

【构造邻接矩阵】

for (int i = 0; i < m; i++)
	{
		int s1, s2;
		cin >> s1 >> s2 ;
		G1->setEdge(G1->locateVex(s1), G1->locateVex(s2), 1);
	}

时间复杂度：利用循环构造,循环次数与边数m有关，则时间复杂度为θ(m)
空间复杂度：利用二维指针存储边信息，与边数n有关，空间复杂度为θ(n*n)

【DFS算法将二维数组进行改变】

void DFS(Graph *G,int v,int s)
{
   	G->setMark(v,1);
   	du[v+1][s+1]=du[s+1][v+1]=1;
    for(int w=G->first(v);w<G->n();w=G->next(v,w))
        if(G->getMark(w)==0&&G->weight(v, w)!=0)
            DFS(G,w,s);
}

时间复杂度：利用DFS递归遍历,递归遍历了n个顶点，时间复杂度为θ(n)
空间复杂度：利用二维数组存储顶点与顶点信息，与边数n有关，空间复杂度为θ(n*n)

【计数器通过循环计数】

for(int i=1;i<=n;i++){
		int j;
		for(j=1;j<=n;j++){
			if(du[i][j]==0) break;
		}
		if(j==n+1) cmp++;
}

时间复杂度：利用双层循环,循环次数与边数n有关，其他操作所用时间开销与输入规模无关，则时间复杂度为θ(n*n)
空间复杂度：利用一个临时变量进行计数，空间复杂度为θ(1)

四.源代码设计

【ADT设计】

#ifndef GRAPH
#define GRAPH
class Graph{
public:
	Graph() {} // 默认构造函数
	//初始化一个有n个顶点的图
	virtual void Init(int n) = 0;
	//返回:顶点和边的数量
	virtual int n() = 0;
	virtual int e() = 0;
	// 返回v的第一个邻居 
	virtual int first(int v) =0;
	// 返回v的下一个邻居
	virtual int next(int v, int w) =0;
	//找到(包含实际信息的）顶点在图中的位置 
	virtual int locateVex(char u) = 0;
	//返回某个顶点的值(实际信息) 
	virtual int getVex(int v) = 0;
	//给某个顶点赋值
	virtual void putVex(int v, int value) = 0;
	//设置边的权重
	virtual void setEdge(int v1, int v2, int wght) = 0;
	// Return:边i、j或0的权值
	virtual int weight(int v1, int v2) = 0;
	//获取并设置顶点的标记值
	// v:顶点
	// val:要设置的值
	virtual int getMark(int v) =0;
	virtual void setMark(int v, int val) =0;
};
#endif

【ADT实现】

#include "iostream"
#include "graph.h"
using namespace std;
class Graphm : public Graph{
private:
    int numVertex, numEdge; //顶点数,边数
    int *vexs;//存储顶点信息
    int *mark;       //标记数组的指针
    int **matrix;   //邻接矩阵的指针 
public:
	Graphm(int numVert)     // 构造函数
    { 
		Init(numVert); 
	}
    //初始化一个有n个顶点的图
	void Init(int n)override 
	{ 
		int i;
		numVertex = n;
		numEdge = 0;
		vexs=(int *) new int[numVertex];
		mark=(int *) new int[numVertex];
		matrix = (int**) new int*[numVertex]; 
		for (i=0; i<numVertex; i++)
		{
			mark[i]=0;
		 	matrix[i] = new int[numVertex];
		}
		for (i=0; i< numVertex; i++) 
		  	for (int j=0; j<numVertex; j++)
		   		matrix[i][j] = 0;
	}
    int n()override { return numVertex; } 
    int e()override { return numEdge; }  
    // 返回v的第一个邻居
	int first(int v)override {
	    for (int i=0; i<numVertex; i++)
	      	if (matrix[v][i] != 0) return i;
	    	return numVertex;           // Return n if none
	}
  	// 返回v在w之后的邻居
 	int next(int v, int w)override {
   		for(int i=w+1; i<numVertex; i++)
    		if (matrix[v][i] != 0) return i;
    return numVertex;           // Return n if none
  	}
    /**返回顶点在图中的位置**/
    int locateVex(char u)override {
        for (int i = 0; i < numVertex; i++) 
		{
            if (u==vexs[i])	return i;
        }
        return -1;
    }
    /**返回某个顶点的值(实际信息) **/
  	int getVex(int v)override {
        return vexs[v];
    }
    /**给某个顶点赋值**/
    void putVex(int v, int value)override {
        vexs[v] = value;
    }
    //将边(v1, v2)设为“wt”
    void setEdge(int v1, int v2, int wt)override {
        if (matrix[v1][v2] == 0)
            numEdge++;
        matrix[v1][v2] = wt;
    }
	// Return:边i、j或0的权值
    int weight(int v1, int v2)override { return matrix[v1][v2]; }
    //获取并设置顶点的标记值
	// v:顶点
	// val:要设置的值
    int getMark(int v)override { return mark[v]; }
  	void setMark(int v, int val)override { mark[v] = val; }
};

【主函数设计】

#include "graphm.h"
#include "graph.h"
using namespace std;
int du[100][100];
void DFS(Graph *G,int v,int s)
{
   	G->setMark(v,1);
   	du[v+1][s+1]=du[s+1][v+1]=1;
    for(int w=G->first(v);w<G->n();w=G->next(v,w))
        if(G->getMark(w)==0&&G->weight(v, w)!=0)//没被访问过且存在边(v,j)
            DFS(G,w,s);
}
int main() {
	int n, m;
	cin >> n >> m;
	Graphm *G1 = new Graphm(n);
	for (int i = 1; i <= n; i++)
	{
		G1->putVex(i-1, i);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
			du[i][j]=0;
	}
	for (int i = 0; i < m; i++)
	{
		int s1, s2;
		cin >> s1 >> s2 ;
		G1->setEdge(G1->locateVex(s1), G1->locateVex(s2), 1);
	}
	int cmp = 0;
	for (int i = 0; i < n; i++)
	{
		for(int j=0;j<n;j++)
		{
			G1->setMark(j,0);
		}
		DFS(G1,i,i);
	}
	for(int i=1;i<=n;i++){
		int j;
		for(j=1;j<=n;j++){
			if(du[i][j]==0) break;
		}
		if(j==n+1) cmp++;
	}
	cout << cmp; 
	return 0;
}