【文章解读】Sparse Bayesian learning for off-grid DOA estimation with nested arrays，稀疏贝叶斯学习，离格，DOA估计，信号处理

晚安66

已于 2024-05-24 18:46:25 修改

阅读量754

点赞数 28

分类专栏：科研文章标签：科研

于 2024-05-14 16:55:19 首次发布

本文链接：https://blog.csdn.net/qq_45765437/article/details/138860994

版权

科研专栏收录该内容

1 篇文章 0 订阅

订阅专栏

导读

本文将粗略解读18-DSP-Chen-Sparse Bayesian learning for off-grid DOA estimation with nested arrays，博主才学疏浅，如有错误，多多海涵。希望能找到志同道合的伙伴一起研究SBL，大家有什么问题可以留言交流。

信号模型

假设阵列接收信号为 $\bf{X}$ ，那么接受信号的协方差矩阵为：

$\bf{R}_x=E\left \{ \bf{x}(t)\bf{x}^H(t)\right \}=\bf{A}\bf{R}_s\bf{A}^H+\sigma^2_n \bf{I}_M.$

简单说明一下。假设 $\mathbf{A}=\left[ \mathbf{a}\left( {{\theta }_{1}} \right),\cdots ,\mathbf{a}\left( {{\theta }_{k}} \right),\cdots ,\mathbf{a}\left( {{\theta }_{K}} \right) \right]$ ， $\mathbf{a}\left( {{\theta }_{k}} \right)={{\left[ {{a}_{1}},\cdots ,{{a}_{M}} \right]}^{T}}$ ，那么观测信号协方差阵表示为：

$\mathbf{A}{{\mathbf{R}}_{s}}{{\mathbf{A}}^{H}}=\left[ \mathbf{a}\left( {{\theta }_{1}} \right){{\mathbf{a}}^{H}}\left( {{\theta }_{1}} \right),\mathbf{a}\left( {{\theta }_{2}} \right){{\mathbf{a}}^{H}}\left( {{\theta }_{2}} \right),\cdots ,\mathbf{a}\left( {{\theta }_{k}} \right){{\mathbf{a}}^{H}}\left( {{\theta }_{k}} \right) \right]{{\left[ \sigma _{1}^{2},\cdots ,\sigma _{K}^{2} \right]}^{T}}.$

又因为有 $vec\left( \mathbf{a}\left( {{\theta }_{k}} \right){{\mathbf{a}}^{H}}\left( {{\theta }_{k}} \right) \right)=\left[ \begin{matrix} a_{1}^{*}\mathbf{a}\left( {{\theta }_{k}} \right) \\ a_{2}^{*}\mathbf{a}\left( {{\theta }_{k}} \right) \\ \vdots \\ a_{M}^{*}\mathbf{a}\left( {{\theta }_{k}} \right) \\ \end{matrix} \right]={{\mathbf{a}}^{*}}\left( {{\theta }_{k}} \right)\otimes \mathbf{a}\left( {{\theta }_{k}} \right)$ ，所以将 ${{\mathbf{R}}_{x}}$ 进行向量化可以得到：

$\mathbf{y}\triangleq vec\left( {{\mathbf{R}}_{x}} \right)=\left( {{\mathbf{A}}^{*}}\diamond \mathbf{A} \right)\mathbf{p}+\sigma _{n}^{2}vec\left( {{\mathbf{I}}_{M}} \right),$

其中， $\diamond$ 代表khtari-rao积， $\mathbf{p}={{\left[ \sigma _{1}^{2},\cdots ,\sigma _{K}^{2} \right]}^{T}}$ 是源功率向量。

为了方便后续表示，令 ${{\mathbf{A}}^{*}}\diamond \mathbf{A}\triangleq \mathbf{\bar{A}}=\left[ \mathbf{\bar{a}}\left( {{\theta }_{1}} \right),\cdots ,\mathbf{\bar{a}}\left( {{\theta }_{N}} \right) \right]\in {{\mathbb{C}}^{{{M}^{2}}*N}}$ ， $\mathbf{\bar{a}}\left( {{\theta }_{k}} \right)={{\mathbf{a}}^{*}}\left( {{\theta }_{k}} \right)\otimes \mathbf{a}\left( {{\theta }_{k}} \right)\in {{\mathbb{C}}^{{{M}^{2}}*1}}$ 。其中， $\otimes$ 代表克罗内克积。

真实情况的协方差阵只能用有限快拍数去近似：

${{\mathbf{\hat{R}}}_{x}}=\frac{1}{T}\sum\limits_{t=1}^{T}{\mathbf{x}\left( t \right){{\mathbf{x}}^{H}}\left( t \right)}.$

所以，真实的向量化之后的协方差矩阵用 $\mathbf{\hat{y}}$ 表示：

$\mathbf{\hat{y}}\triangleq vec\left( {{\mathbf{R}}_{x}} \right)=\left( {{\mathbf{A}}^{*}}\diamond \mathbf{A} \right)\mathbf{p}+\sigma _{n}^{2}vec\left( {{\mathbf{I}}_{M}} \right)+\mathbf{\varepsilon },$

其中， $\mathbf{\varepsilon }=vec\left( \mathbf{\hat{y}}-\mathbf{y} \right)$ 代表采样得到的协方差和真实协方差之间的误差。由中心极限定理，该误差的概率密度服从正态分布[1]:

$\mathbf{\varepsilon }\sim CN\left( {{\mathbf{0}}_{{{M}^{2}}}},\mathbf{W} \right),$

其中， $\mathbf{W}=\frac{1}{T}{{\mathbf{R}}_{x}}\otimes {{\mathbf{R}}_{x}}\approx \frac{1}{T}{{\mathbf{\hat{R}}}_{x}}\otimes {{\mathbf{\hat{R}}}_{x}}$ 。和OGSBL一样，也考虑离格误差，并用一阶泰勒展开近似。因此有 $\mathbf{\Phi }\left( \beta \right)=\mathbf{A}+\mathbf{B}diag\left\{ \beta \right\}$ 。

那么整体信号模型表示为：

$\mathbf{\hat{y}}=\underbrace{\left[ \begin{matrix} \mathbf{\Phi }\left( \beta \right) & {{\mathbf{1}}_{n}} \\ \end{matrix} \right]}_{\triangleq \mathbf{\bar{\Phi }}\left( \beta \right)}\underbrace{\left[ \begin{matrix} \mathbf{p} \\ \sigma _{n}^{2} \\ \end{matrix} \right]}_{\triangleq \mathbf{\bar{p}}}+\mathbf{\varepsilon }.$

那么接收信号服从复高斯分布：

$p\left( \mathbf{\hat{y}}|\mathbf{\bar{p}};\beta ,\mathbf{W} \right)=CN\left( \mathbf{\hat{y}}|\mathbf{\bar{\Phi }}\left( \beta \right)\mathbf{\bar{p}},\mathbf{W} \right).$

信源服从功率 $\bf{\delta}$ 的复高斯分布：

$p\left( \mathbf{\bar{p}}|\mathbf{\delta } \right)=CN\left( \mathbf{\bar{p}}|\mathbf{0},\mathbf{\Delta } \right),$

其中， $\mathbf{\Delta }=diag\left( \mathbf{\delta } \right)$ ， $\mathbf{\delta }={{\left[ {{\delta }_{1}},\cdots ,{{\delta }_{N}} \right]}^{T}}$ 。那么超参数 ${{\delta }_{i}}$ 服从独立的伽马分布：

$p\left( \mathbf{\delta } \right)=\prod\limits_{i=1}^{N+1}{\Gamma \left( {{\delta }_{i}};1,\rho \right)}$

其中， $\rho$ 是一个很小的正数（例如，0.01）。

下面整理一下矩阵的维度： $\mathbf{\Sigma }\in {{\mathbb{C}}^{N*N}},\mathbf{\bar{A}}\in {{\mathbb{C}}^{{{M}^{2}}*N}},\mathbf{\hat{y}}\in {{\mathbb{C}}^{{{M}^{2}}*1}},\mathbf{\mu }\in {{\mathbb{C}}^{N*1}}$ ，然后开始证明 $\mathbf{\bar{p}}$ 的后验服从一个复高斯分布。

已知 $\bf{W}$ 和 $\bf{\beta}$ 与 $\bar{\bf{p}}$ 无关，那么有 $p\left( \mathbf{\bar{p}}|\mathbf{\delta } \right)=p\left( \mathbf{\bar{p}}|\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)=\frac{p\left( \mathbf{\bar{p}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)}{p\left( \mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)}$ 。 $\mathbf{\delta }$ 相对于 $\mathbf{\hat{y}}$ 独立，有 $p\left( \mathbf{\hat{y}}\mathbf{\bar{p}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)=p\left( \mathbf{\hat{y}}\mathbf{\bar{p}},\mathbf{W},\mathbf{\beta } \right)$

$p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)=\frac{p\left( \mathbf{\hat{y}}|\mathbf{\bar{p}},\mathbf{W},\mathbf{\beta } \right)p\left( \mathbf{\bar{p}}\mathbf{\delta } \right)}{\int{p\left( \mathbf{\hat{y}}|\mathbf{\bar{p}},\mathbf{W},\mathbf{\beta } \right)p\left( \mathbf{\bar{p}}|\mathbf{\delta } \right)d\mathbf{\bar{p}}}}$

那么上述公式分子部分表示为：

$p\left( \mathbf{\hat{y}}|\mathbf{\bar{p}},\mathbf{W},\mathbf{\beta } \right)p\left( \mathbf{\bar{p}}|\mathbf{\delta } \right)=\frac{{{\left| \mathbf{W} \right|}^{-1}}}{{{\pi }^{{{M}^{2}}+N}}\left| \mathbf{\Delta } \right|}\exp \left\{ -\left( {{{\mathbf{\hat{y}}}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}}-{{{\mathbf{\hat{y}}}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi \bar{p}}-{{{\mathbf{\bar{p}}}}^{H}}{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}} \right)-{{{\mathbf{\bar{p}}}}^{H}}\left( {{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi }+{{\mathbf{\Delta }}^{-1}} \right)\mathbf{\bar{p}} \right\}$

要最大化后验概率 $p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)$ 的对数似然函数 $\ln p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)$ 实际上就是分子求导，求一阶零点，得到极大值，再将零点带入分母部分。令上式指数括号中的部分为 $L\left( {\mathbf{\bar{p}}} \right)$ ：

$\begin{aligned} L\left( {\mathbf{\bar{p}}} \right)=-\left( {{{\mathbf{\hat{y}}}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}}-{{{\mathbf{\hat{y}}}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi \bar{p}}-{{{\mathbf{\bar{p}}}}^{H}}{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}} \right)-{{\mathbf{\bar{p}}}^{H}}\left( {{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi }+{{\mathbf{\Delta }}^{-1}} \right)\mathbf{\bar{p}}\end{aligned}$

式子当中 ${{\mathbf{\hat{y}}}^{H}}$ ， $\mathbf{\hat{y}}$ ， $\mathbf{W}$ ， $\mathbf{\Phi }$ ， ${{\mathbf{\Phi }}^{H}}$ ， ${{\mathbf{\bar{p}}}^{H}}$ 和 $\mathbf{\Delta }$ 都是与 $\mathbf{\bar{p}}$ 无关的量。

因此，我们对 $L\left( {\mathbf{\bar{p}}} \right)$ 求导，取零点得： $\mathbf{\bar{p}}={{\left({{\mathbf{\Phi}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi}+{{\mathbf{\Delta}}^{-1}}\right)}^{-1}}{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}}$ 。 $\left( {{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi }+{{\mathbf{\Delta }}^{-1}} \right)$ 和 $\mathbf{W}$ 是实对称阵。然后我们将零点带回 $L\left( {\mathbf{\bar{p}}} \right)$ 得：

$L{{\left({\mathbf{\bar{p}}} \right)}_{\mathbf{\bar{p}}={{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}}={{\left( {{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi}+{{\mathbf{\Delta}}^{-1}}\right)}^{-1}}{{\mathbf{\Phi}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}}}}=-{{\mathbf{\hat{y}}}^{H}}{{\mathbf{W}}^{-1}}\left[\mathbf{W}-\mathbf{\Phi}\left({{\mathbf{\Phi}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi}+{{\mathbf{\Delta}}^{-1}}\right){{\mathbf{\Phi }}^{H}} \right]{{\mathbf{W}}^{-1}}\mathbf{\hat{y}}$

令 $\mathbf{\Sigma }\triangleq {{\left( {{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi }+{{\mathbf{\Delta }}^{-1}} \right)}^{-1}}$ ，再根据Woodbury矩阵引理，有:

${{\mathbf{W}}^{-1}}\left( \mathbf{W}-\mathbf{\Phi }{{\mathbf{\Sigma }}^{-1}}{{\mathbf{\Phi }}^{H}} \right){{\mathbf{W}}^{-1}}={{\left( \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)}^{-1}}$

因此信号 $\mathbf{\bar{p}}$ 的后验概率分母部分可以表示为：

$p\left(\mathbf{\hat{y}}|\mathbf{\delta},\mathbf{W},\mathbf{\beta} \right)=D\frac{1}{{{\pi}^{{{M}^{2}}}}\left|\mathbf{W}+\mathbf{\Phi \Delta}{{\mathbf{\Phi}}^{H}} \right|}\exp\left\{-{{{\mathbf{\hat{y}}}}^{H}}{{\left(\mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)}^{-1}}\mathbf{\hat{y}} \right\}$

其中，常数 $\mathbf{D}=\frac{\left| \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right|}{{{\pi }^{N}}\left| \mathbf{\Delta } \right|\left| \mathbf{W} \right|}$ 。那么可以看出随机变量：

$p\left( \mathbf{\hat{y}}|\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)\sim CN\left( \mathbf{0},\mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)$

那么 $\mathbf{\bar{p}}$ 的后验概率表示为：

$p\left( \mathbf{\bar{p}}| \mathbf{\hat{y}},\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)=\exp \left\{ -{{\left( \mathbf{\bar{p}}-\mathbf{\Sigma }{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}} \right)}^{H}}{{\mathbf{\Sigma }}^{-1}}\left( \mathbf{\bar{p}}-\mathbf{\Sigma }{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}} \right) \right\}$

因此 $\mathbf{\bar{p}}$ 的后验服从复高斯分布：

$p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta };\beta \right)=CN\left( \mathbf{\bar{p}}|\mathbf{\mu },\mathbf{\Sigma } \right)$

其中， $\mathbf{\mu }=\mathbf{\Sigma }{{\mathbf{\bar{\Phi }}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\hat{y}},\mathbf{\Sigma }={{\left( {{{\mathbf{\bar{\Phi }}}}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\bar{\Phi }}+{{\mathbf{\Delta }}^{-1}} \right)}^{-1}}$ 。

接下来用第二类估计函数估计超参数 $\bf{\delta}$ ，第二类估计函数定义为：

${{L}_{II}}\left( \mathbf{\delta },\mathbf{\beta } \right)=E{{\left\{ \ln p\left( \mathbf{\bar{p}},\mathbf{\hat{y}},\mathbf{\delta },\mathbf{\beta } \right) \right\}}_{p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta },\mathbf{\beta } \right)}}=E{{\left\{ \ln p\left( \mathbf{\hat{y}}|\mathbf{\bar{p}},\mathbf{\beta } \right)p\left( \mathbf{\bar{p}}|\mathbf{\delta } \right)p\left( \mathbf{\delta } \right) \right\}}_{p\left( \mathbf{\bar{p}}|\mathbf{\hat{y}},\mathbf{\delta },\mathbf{\beta } \right)}}$

已知 $p\left( \mathbf{\hat{y}}|\mathbf{\delta },\mathbf{W},\mathbf{\beta } \right)\sim CN\left( \mathbf{0},\mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)$ ，那么有：

$\begin{aligned} \ln p\left( \mathbf{\hat{y}}|\mathbf{\delta },\mathbf{\beta } \right)p\left( \mathbf{\delta } \right)\propto -\ln \left| \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right|-{{\mathbf{\hat{y}}}^{H}}{{\left( \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)}^{-1}}\mathbf{\hat{y}}-\sum\limits_{n=1}^{N+1}{\rho {{\delta }_{n}}} \end{aligned}$

根据行列式转换定理： $\left| \mathbf{A} \right|\left| {{\beta }^{-1}}\mathbf{I}+\mathbf{B}{{\mathbf{A}}^{-1}}{{\mathbf{B}}^{H}} \right|=\left| {{\beta }^{-1}}\mathbf{I} \right|\left| \mathbf{A}+\beta {{\mathbf{B}}^{H}}\mathbf{B} \right|$ ，我们令 $\mathbf{A}={{\mathbf{\Delta }}^{-1}},\mathbf{B}={{\mathbf{W}}^{-\frac{1}{2}}}\mathbf{\Phi },\beta =1$ ，则上式转换成:

$\left| \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right|=\left| {{\mathbf{W}}^{\frac{1}{2}}} \right|\frac{\left| {{\mathbf{\Delta }}^{-1}}+{{\mathbf{\Phi }}^{H}}{{\mathbf{W}}^{-1}}\mathbf{\Phi } \right|}{\left| {{\mathbf{\Delta }}^{-1}} \right|}\left| {{\mathbf{W}}^{\frac{1}{2}}} \right|=\left| {{\mathbf{W}}^{\frac{1}{2}}} \right|\frac{\left| {{\mathbf{\Sigma }}^{-1}} \right|}{\left| {{\mathbf{\Delta }}^{-1}} \right|}\left| {{\mathbf{W}}^{\frac{1}{2}}} \right|$

因此， $\ln \left| \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right|\propto -\ln \left| \mathbf{\Sigma } \right|+\ln \left| \mathbf{\Delta } \right|$ 。又有 ${{\mathbf{\hat{y}}}^{H}}{{\left( \mathbf{W}+\mathbf{\Phi \Delta }{{\mathbf{\Phi }}^{H}} \right)}^{-1}}\mathbf{\hat{y}}={{\left( \mathbf{\hat{y}}-\mathbf{\Phi }{{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}} \right)}^{H}}{{\mathbf{W}}^{-1}}\left( \mathbf{\hat{y}}-\mathbf{\Phi }{{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}} \right)+\mathbf{\mu }_{_{{\mathbf{\bar{p}}}}}^{H}{{\mathbf{\Delta }}^{-1}}{{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}}$ ，

$\left| \mathbf{\Delta } \right|=\left| diag\left( \mathbf{\delta } \right) \right|={{\delta }_{1}}{{\delta }_{2}}\ldots {{\delta }_{n}},\ln \left| \mathbf{\Delta } \right|=\sum\limits_{n=1}^{N+1}{\ln {{\delta }_{n}}}$ 。因此，原来的对数似然函数等价于：

$\ln p\left( \mathbf{\hat{y}}|\mathbf{\delta },\mathbf{\beta } \right)p\left( \mathbf{\delta } \right)\propto \ln \left| \mathbf{\Sigma } \right|-\sum\limits_{n=1}^{N}{\ln {{\delta }_{n}}}-\sum\limits_{n=1}^{N}{\delta _{n}^{-1}{{\left| {{\mathbf{\mu }}^{n}} \right|}^{2}}}-\sum\limits_{n=1}^{N+1}{\rho {{\delta }_{n}}}$

这里将 ${{\left( \mathbf{\hat{y}}-\mathbf{\Phi }{{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}} \right)}^{H}}{{\mathbf{W}}^{-1}}\left( \mathbf{\hat{y}}-\mathbf{\Phi }{{\mathbf{\mu }}_{{\mathbf{\bar{p}}}}} \right)$ 视作无关项，再根据行列式求导公式：

$\frac{\partial \ln \left| \mathbf{\Sigma } \right|}{\partial {{\delta }_{n}}}=-\frac{\partial \ln \left| {{\mathbf{\Sigma }}^{-1}} \right|}{\partial {{\delta }_{n}}}=-tr\left( \frac{\partial {{\mathbf{\Sigma }}^{-1}}}{\partial {{\delta }_{n}}}\mathbf{\Sigma } \right)=\frac{{{\mathbf{\Sigma }}_{nn}}}{\delta _{n}^{2}}$

对其求导得一元二次方程： $\rho\delta_{n}^{2}+{{\delta}_{n}}-\left( \mathbf{\mu }{{\mathbf{\mu }}^{H}}+\mathbf{\Sigma } \right)=0$ 。取零点可得：

$\delta _{n}^{new}=\frac{-1+\sqrt{1+4\rho \left( \mathbf{\mu }{{\mathbf{\mu }}^{H}}\mathbf{+\Sigma } \right)}}{2\rho }$

因此，功率迭代公式得到证明。

离格部分别的博主已经有证明过了，这里不在赘述。

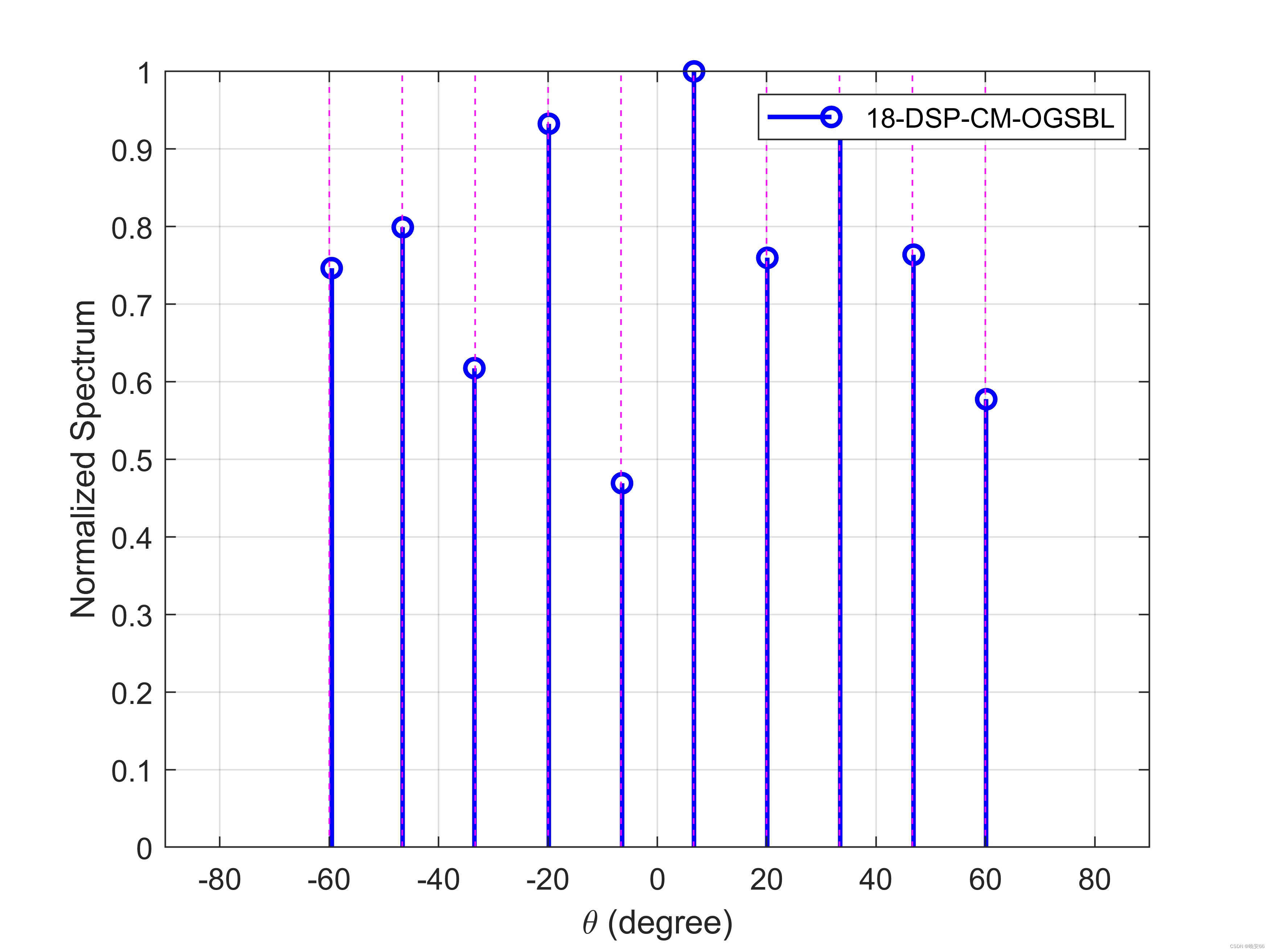
仿真实验

角度	-60，60之间均匀分布10个源
信噪比	0dB
扰噪比	无
快拍数	200
先验网格分辨率	1°
阵元数	（3,4）二阶扩展差分互质阵

function [Pm, search_range, iter]=Bayesian_DSP2018(X, nSnapshot, search_step, MicP, etc, d, maxiter, tol)
search_range=[-90:search_step:90];	% 搜索区域
Rxx=X*X'/nSnapshot;             	% 协方差矩阵
Y=Rxx(:);                       % 矢量化
[nMic2,T]=size(Y);
nMic=sqrt(nMic2);
nGrid=length(search_range);% 网格点数
In=eye(nMic);
In=In(:); % 单位阵矢量化
pos_all=round(log(kron(exp(-MicP),exp(MicP))));% 虚拟阵元
% ans1 = unique(pos_all); % 自由度DOF = 虚拟阵元数量（包含正、负位置的阵元）
W=kron(Rxx.',Rxx)/nSnapshot;
W_sq=sqrtm(inv(W));
Y=W_sq*Y;
% ans1 = sqrt(nSnapshot)*In;
%% Initialization
beta0=1;
delta=ones(nGrid+1,1);
a_search=search_range*pi/180; % 角度转弧度
A=exp(-1i*pi*pos_all'*sin(a_search));   % 虚拟阵元阵列流型
B=-1i*pi*pos_all'*cos(a_search).*A;
% a_search=search_area*pi/180; % 角度转弧度
% A=exp(-1i*pi*pos_all'*sind(search_area));   % 虚拟阵元阵列流型
% B=-1i*pi*pos_all'*cosd(search_area).*A;
A_w=W_sq*A;
B_w=W_sq*B;
I_w= W_sq* In;
Phi=[A_w, I_w]; %公式13

% V_temp=  1/beta0*eye(nMic2) +  Phi *diag(delta) * Phi';
% Sigma = diag(delta) -diag(delta) * Phi' * (V_temp\Phi) *  diag(delta); % 公式19
% mu = beta0*Sigma * Phi' * Y; % 公式18

converged = false;
iter = 0;
while (~converged) || iter<=100   
    iter = iter + 1;
    delta_last = delta;
    %% Calculate mu and Sigma
    V_temp=  1/beta0*eye(nMic2) +  Phi *diag(delta) * Phi';
    Sigma = diag(delta) -diag(delta) * Phi' * (V_temp\Phi) *  diag(delta);
    mu = beta0*(Sigma * (Phi' * Y));
    
    %% Update delta
    temp=sum( mu.*conj(mu), 2) + T*real(diag(Sigma));
    delta= ( -T+ sqrt(  T^2 + 4*d* real(temp) ) ) / (  2*d   );
    
    %% Stopping criteria
    erro=norm(delta - delta_last)/norm(delta_last);% 收敛条件
    if erro < tol || iter >= maxiter
        converged = true;
    end
    
    %% Grid refinement
    [~, idx] = sort(delta(1:end-1), 'descend');
    idx = idx(1:etc);
    BHB = B_w' * B_w;
    P = real(conj(BHB(idx,idx)) .* (mu(idx,:) * mu(idx,:)' + Sigma(idx,idx)));
    v =  real(diag(conj(mu(idx))) * B_w(:,idx)' * (Y - A_w * mu(1:end-1)-mu(end)*I_w))...
        -  real(diag(B_w(:,idx)' * A_w * Sigma(1:end-1,idx)) + diag(Sigma(idx,nGrid+1))*B_w(:,idx).'*conj(I_w));
    eigP=svd(P);
    if eigP(end)/eigP(1)>1e-5
        temp1 =  P \ v;
    else
        temp1=v./diag(P);
    end
    temp2=temp1'*180/pi;
    if iter<100
        ind_small=find(abs(temp2)<search_step/100);
        temp2(ind_small)=sign(temp2(ind_small))*search_step/100;
    end
    ind_large=find(abs(temp2)>search_step);
    temp2(ind_large)=sign(temp2(ind_large))*search_step/100;
    angle_cand=search_range(idx) + temp2;
    search_range(idx)=angle_cand;
%     for iii=1:etc
%         if angle_cand(iii)>= search_mid_left(idx(iii))  && (angle_cand(iii) <= search_mid_right(idx(iii)))
%             search_area(idx(iii))=angle_cand(iii);
%         end
%     end
    A_ect=exp(-1i*pi*pos_all'*sin(search_range(idx)*pi/180));
    B_ect=-1i*pi*pos_all'*cos(search_range(idx)*pi/180).*A_ect;
    A_w(:,idx) =W_sq*A_ect;
    B_w(:,idx) =W_sq*B_ect;
    Phi(:,idx)= A_w(:,idx);
end
Pm=delta(1:end-1);
end
% [search_area,sort_s]=sort(search_area);
% Pm=Pm(sort_s);
% insert=(search_area(1:end-1)+search_area(2:end))/2;
% search_area_2=zeros(length(search_area)*2-1,1);
% search_area_2(1:2:end)=search_area;
% search_area_2(2:2:end)=insert;
% Pm_2=zeros(length(Pm)*2-1,1);
% Pm_2(1:2:end)=Pm;
% search_area=search_area_2;
% Pm=Pm_2;

参考文献

[1] 1998-DSP-Covariance matching estimation techniques for array signal processing applications

[2] 2018-DSP-Sparse Bayesian learning for off-grid DOA estimation with nested arrays

晚安66

关注

28
点赞
踩
6

收藏

觉得还不错? 一键收藏
打赏
0
评论
【文章解读】Sparse Bayesian learning for off-grid DOA estimation with nested arrays，稀疏贝叶斯学习，离格，DOA估计，信号处理

本文将粗略解读18-DSP-Chen-Sparse Bayesian learning for off-grid DOA estimation with nested arrays，博主才学疏浅，如有错误，多多海涵。希望能找到志同道合的伙伴一起研究SBL，大家有什么问题可以留言交流。
复制链接

扫一扫