Dp-状态压缩：蒙德里安的梦想 详解版

题目链接：https://www.acwing.com/problem/content/description/293/

思路分析：

这种棋盘类型的问题+数据范围。看起来就巨像状态压缩。

把整个棋盘划分为若干个1x1的小格子，那么，问题就转化为了用1x2的小长方形去将整个棋盘填充满，总共有多少种方案。此外，注意到，当我们将所有横向的小长方形都已经摆放(填充)完成后，所有纵向的小长方形的摆放方式也就唯一确定了，那么，总的方案数就等于摆完所有横向长方形的方案数。所以，我们只用考虑如何枚举横向长方形的摆放即可

状态表示

因此，我们全篇只需要考虑摆放横着的小长方形。这时候我们需要以每一列为不同的阶段进行划分。

其实，反过来也一样的啦，当我们只考虑竖着拜访的小长方形的时候，我们需要以不同的行 为阶段进行划分。

状态压缩dp的经典问题：对于每一列不同的m个格子，对应的二进制数的不同的位表示什么？

如果对应的位置有伸出来小格子就为1，否则为0。只能这样表示，要不怎么表示呢？

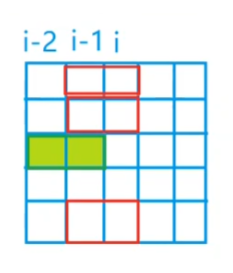
因此f[i][j]表示，前i-1列已经摆好，第i列的伸出情况的对应二进制表示为j的所有情况的种数。

ok，接下来就是需要考虑i-1到i列如何进行合法地转换？

状态转换

显然，对于f[i][j], 需要考虑到f[i-1][k], 其中k在是i-1列中，可以合法地转移到i列，且第i列状态为j的所有可能情况。

f[i][j] = Σf[i-1][k]

现在我们考虑，对于j，哪些k是合法的即可。

• 转移的合法性限制
  如果j的某一位为1，代表从i-1列到i列放了一个小正方形。显然，此时，i-2列到i-1就不能再放了，否则会有重叠，也就是说i-1列中，这个对应的位就不能再是1了。合法的转移对应的数学表示为：j & k == 0

• i-1列自身的合法性限制

以下代码判断一个数i，是否有连续为偶数个0

			st[i] = true;
//            记录一列中0的个数
            int cnt = 0;
            for (int j = 0; j < n; j++) {
				// 找出来位置上为1的二进制位
                if (i >> j & 1) {
                	// 如果这个1之前连续的0为奇数
                    if (cnt & 1) {
                        st[i] = false;
                        break;
                    }
                }
                // 为偶数，则cnt++
                else cnt++;
            }
            // 特判一下最后一位为0的情况。
			if (cnt & 1) st[i] = false;

对于i-1列的摆放状态，所有连续区域来说，这些区域的长度必须为偶数，否则放不下竖着的小方块了。i-1列的合法性对应的数学表示为：st[j | k] == true
解释一下：
我们要考虑的是第i-1列（第i-1列是这里的主体）中从第i-2列横插过来的，还要考虑自己这一列（i-1列）横插到第i列的。比如 第i-2列插过来的是k=10101，第i-1列插出去到第i列的是 j =01000 。 那么合在第i-1列，到底有多少个1呢？自然想到的就是这两个操作共同的结果：两个状态或。 j | k = 01000 | 10101 = 11101
这个 j|k 就是当前 第i-1列的到底哪几行是横着放格子的
因此，最后这个状态转移的代码表示为：

if ((j & k) == 0 && st[j | k]) 
{
	f[i][j] += f[i - 1][k]; 
}

状态初始化

f[0][0] = 1, f是对状态的计数，不是像线性dp那样，对什么最大值最小值的计数。因此，什么都不放也是一种状态

目标状态

f[m][0] 表示第m + 1列不能有东西捅出来。同时，前m-1列都已经放好了。那么因此，第m列也就确定了。

有了以上的分析，代码就顺理成章了。

#include<bits/stdc++.h>
using namespace std;
const int N = 12, M = 1 << N;
int st[M];
long long f[N][M];


int main(){
    int n, m;
    while (cin >> n >> m && (n || m)){

        for (int i = 0; i < 1 << n; i ++){
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; j ++)
                if (i >> j & 1){
                    if (cnt & 1) st[i] = false; // cnt 为当前已经存在多少个连续的0
                    cnt = 0;
                }
                else cnt ++;
            if (cnt & 1) st[i] = false; // 扫完后要判断一下最后一段有多少个连续的0
        }

        memset(f, 0, sizeof f);
        f[0][0] = 1;
        // 枚举列
        for (int i = 1; i <= m; i ++)
        	// 枚举每一列中所有状态
            for (int j = 0; j < 1 << n; j ++)
            	// 枚举i-1列的所有状态
                for (int k = 0; k < 1 << n; k ++)
                	// 找到合法的转移和合法的i-1列的状态j | k
                    if ((j & k) == 0 && (st[j | k])) 
                        f[i][j] += f[i - 1][k];      
        cout << f[m][0] << endl;
    }
    return 0;
}

但是，我们发现，枚举所有的摆放状态时，共有2^12种情况，显然，这里边有好多数，他们都是有连续奇数个0的，是不满足的。这会很大程度上浪费时间。因此，我们考虑，先在st数组中预处理所有合法的情况，再预处理所有合法转移到state中，这会很大程度节约时间。对应代码如下。

//提高课版本
#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;

typedef long long LL;

const int N=12, M=1<<N;

int n,m;
LL f[N][M];
vector<int> state[M];//存放每个合法的状态
bool st[N];

int main()
{
    while(cin>>n>>m, n||m)
    {
        //第一步预处理，把同一列中奇数
        //个零连在一块的情况找出来
        for(int i=0;i<1<<n;i++)
        {
            int cnt=0;
            st[i]=true;
            for(int j=0;j<n;j++)
                if(i>>j &1)
                {
                    if(cnt&1)
                    {
                        st[i]=false;
                        break;
                    }
                    cnt=0;
                }
                else cnt++;
            
            if(cnt&1) st[i]=false;
        }
        
        //第二步预处理，排除所有的占据i和i+1列的格子
        //和占据i-1和i列的格子重叠在一起的情况
        //同时，把所有的合法情况加入到state中
        for(int i=0;i<1<<n;i++)//枚举第i列
        {
            state[i].clear();//因为有很多轮输入，所有要先把上一轮样例的情况清空了
            for(int j=0;j<1<<n; j++)//枚举第i-1列
                if((i&j)==0&&st[i|j])//如果不重叠并且有偶数个0
                    //相邻的两列最多有2^11 * 2^11种情况
                    //我们只存储合法的情况
                    state[i].push_back(j);
        }
        
        //每一次都要把f数组初始化
        memset(f,0,sizeof f);
        f[0][0]=1;
        for(int i=1;i<=m;i++)//枚举每一列
            for(int j=0;j<1<<n;j++)//枚举每一列的所有状态
                for(auto k: state[j])//只遍历有效的状态即可
                    f[i][j]+=f[i-1][k];
                    
        cout<<f[m][0]<<endl;
    }
    
    return 0;
    
}