【状态压缩dp】蒙德里安的梦想、最短Hamiltona路径

状态压缩dp是动态规划里一种常见类型，顾名思义，状态压缩要把状态表示“压缩一下”，那么何为压缩，下面用两道例题来体会一下“压缩”的概念。

1、蒙德里安的梦想

原题acwing 蒙德里安的梦想

求把 N×M 的棋盘分割成若干个 1×2 的长方形，有多少种方案。
例如当 N=2，M=4 时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。
如下图所示：

输入格式
输入包含多组测试用例。
每组测试用例占一行，包含两个整数 N 和 M。
当输入用例 N=0，M=0 时，表示输入终止，且该用例无需处理。
输出格式
每个测试用例输出一个结果，每个结果占一行。
数据范围
1≤N,M≤11
输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

这道题目的思路就是，先填横向的小长方形，剩下的区域填竖向的小长方形，那么竖向的就只有一种填法了。所以总的填法等于横向小长方形的所有填法。

这里一列一列的思考，想要在当前列填充横向小长方形，就要考虑上一列的横向小长方形是怎么填的，因为只有一列，但是小长方形是1×2的，所以前一列的横向小长方形必然会捅到这一列。这时候就会有人问：那捅到前面一列的呢？捅到前面一列的就算是前面一列捅过来的即可。

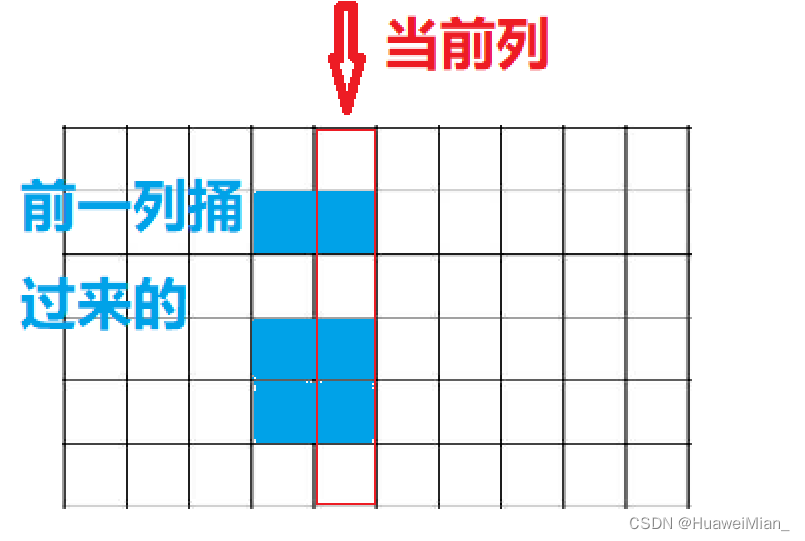
下一步就要开始dp流程了。先思考状态表示，根据上面的推导，得到：
用$f(i,j)$表示第$i-1$列捅到第$i$列的情况是$j$时，前$i$列所有的摆法（比较绕，仔细体会）。首先想想怎么存，可以用1表示捅过来，0表示没有捅过来。想要表示捅过来的情况有点难，但是注意到每个格子只有捅过来和不捅过来这两种情况，所以可以考虑用状态压缩，也即对位进行操作，第几位代表第几列，这一位上是1代表有捅过来的，0代表没有捅过来的。举个例子：

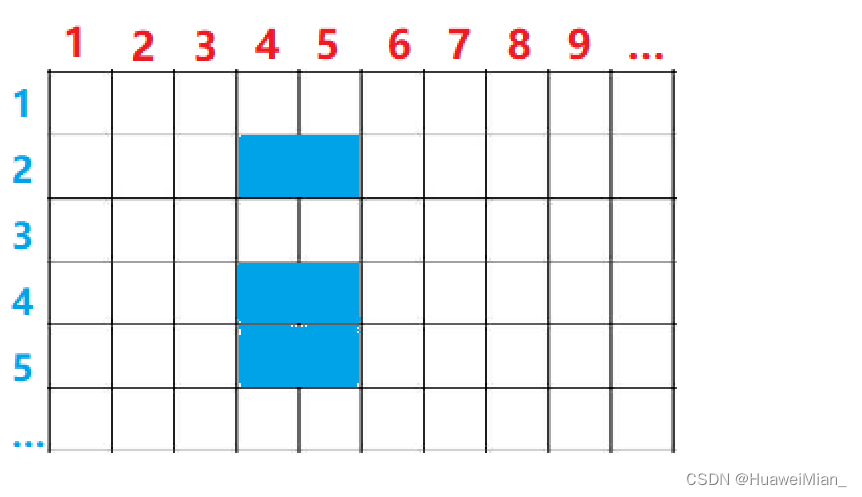
那么第5列被前一列捅过来的情况就是$(011010{)}_2$。转化为十进制就是26。那么就是$f(5,26)$。$f$集合的属性自然就是当前情况下填法的数量。

有了这个，就要考虑怎么状态转移了，现在只看第$i$列和第$i-1$列。要求$f(i,j)$，表示第$i-1$列捅到第$i$列的情况是$j$，想要计算出这种情况下所有的填法，就要找到所有的第$i-2$列捅到第$i-1$列所有合法的填法。第$i-2$列捅到第$i-1$列所有的填法可以用$f(i-1,k)$表示，那么找到合法的k，就可以让$f(i,j)+=f(i-1,k)$了。
为了便于理解，举个具体的例子。假如第三列所有可能的状态有$k_1、k_2、k_3、k_4、k_5、k_6、k_7$，其合法的方案数量分别是$1、3、2、7、5、12、9$，假设现在枚举到了第四列的$j$情况，此时合法的第三列情况有$i_2、i_3、i_6$，那么第四列的$j$情况总合法方案数就是$3+2+12=17$种。以此类推就可以算出第四列的所有情况的合法方案数了。

接下来是看什么样的情况才是合法的。首先要明确一点：$f(i,j)$是第$i-1$列捅到第$i$列的情况，而$f(i-1,k)$是第$i-2$列捅到第$i-1$列的情况。那么来看一看：

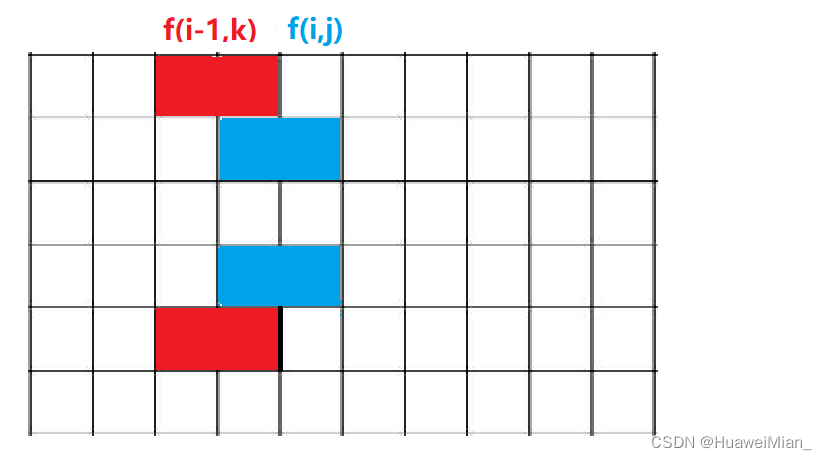
捅到第$i$列是随便的，因为没啥限制。那么就看看第$i-1$列的情况。

1. $k$不能和$j$有一样的位，那样的话就怼到一起了：$(j\&k)==0$；
2. $k$和$j$中间的空隙要是偶数，不然是无法填进去竖向小长方形的。这里判断有点麻烦，所以预先处理出所有可以的情况。假设预处理的情况放到$st$里，那么：$st(j|k)==true$。

其次想想怎么初始化第一列。因为第一列被捅过来的情况一定是$0$，且只假设只有一列的话，一定最多只存在一种填法（全是竖向），所以$f(1,0)=1$。而$f(1,非零)$一定是0，因为不存在有前一列捅到第一列的情况。

最后想想输出结果的时候怎么输出。回想$f(i,j)$的定义：第$i-1$列捅到第$i$列的情况是$j$时，前$i$列所有的摆法。假设有m列，输出$f(m,k)$是不行的，因为这样只包含了m列的一种情况；输出$\Sigma f(m,k)$也是不行的，因为其中存在非法情况（比如捅到m列的间隔有奇数）。那么就要变通一下，求$f(m+1,0)$：因为第$m$列捅到第$m+1$列的情况是0，代表前m列填的满满当当的，这样虽然多了一列，但是最后一列全是竖向的，并无影响。

那么给出题解：

#include <cstring>
#include <iostream>

using namespace std;

const int N = 15, M = 1 << N;

long long f[N][M];
int n, m;
bool st[M];

int main()
{
    while (cin >> n >> m, n || m)
    {
    	//预处理过程，枚举所有状态           
        for (int i = 0; i < 1 << n; i ++ )
        {
        	//cnt记录空隙数量
            int cnt = 0;
            st[i] = true;
            for (int j = 0; j < n; j ++ )
            	//如果到了一个没有空隙的地方，要判断一下之前的空隙是不是奇数
                if (i >> j & 1)
                {
                	//如果是空隙数是奇数，那么这种情况就false
                    if (cnt & 1) st[i] = false;
                    //刷新计数
                    cnt = 0;
                }
                //如果这个位置是空隙，那么cnt++
                else cnt ++ ;
            //最后一个空隙数量
            if (cnt & 1) st[i] = false;
        }
        
        memset(f, 0, sizeof f);
        f[1][0] = 1;
        for (int i = 2; i <= m + 1; i ++ )
            for (int j = 0; j < 1 << n; j ++ )
                for (int k = 0; k < 1 << n; k ++ )
                    if ((j & k) == 0 && st[j | k])
                        f[i][j] += f[i - 1][k];
                        
        cout << f[m + 1][0] << endl;
    }
    
    return 0;
}

分析一下时间复杂度，状态数是 11×2¹¹ ，状态转移的计算量是 2¹¹ ，总共是4×10⁷左右，可以通过。

2、最短Hamilton路径

原题 acwing 最短hamilton路径

给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数，其中第 i 行第 j 个整数表示点 i 到 j 的距离（记为 a[i,j]）。
对于任意的 x,y,z，数据保证 a[x,x]=0，a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数，表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤10⁷
输入样例：

5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0

输出样例：

18

乍一看好像最短路，但是细看的话是不符合最短路的描述的。其实这是一道dp问题。

首先考虑状态表示，用$f(i,j)$代表走到第$j$个点的所有路径，其中用$i$表示已经走过的点。这里也是考虑状态压缩，用每一位代表每一个点，当前位是1就表示该点在路径里，是0就表示该点不在路径里。集合属性自然就是最小路径。

然后考虑状态计算，这里可以把每个集合划分为倒数第二个点是点k的走法。也就是： f ( i , j ) = f ( i − { j } , k ) + a ( k , j ) f(i,j)=f(i-\{j\},k)+a(k,j) f(i,j)=f(i−{j},k)+a(k,j)，其中 i − { j } i-\{j\} i−{j}代表在当前路径种把最后一个点去掉。这题的思路要比上一题简单，接下来就是处理一些细节问题了。

1. 每个集合最开始都是无穷大，因为要找最小路径，无穷大代表当前路径不存在。初始时$f(1,0)=0$，因为起点就是点0；
2. 只有$f(i,j)$中包含点$j$时才进行递推，也就是$i>>j\&1==1$；
3. 划分集合进行计算时，只有$f(i,j)$中包含点$k$时才进行划分，也就是$i>>k\&1==1$；
4. 最后输出时，要让$i$的前$n-1$位都是1，且$j=n-1$代表终点是最后一个点。

给出题解：

#include <iostream>
#include <cstring>

using namespace std;

const int N = 20, M = 1 << N;

int n;
int d[N][N];
int f[M][N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < n; j ++ )
            cin >> d[i][j];
            
    memset(f, 0x3f, sizeof f);
    f[1][0] = 0;
    
    //这里i+=2即可。因为i表示走过的点，而走过的点必然是包含点0的
    //所以每次自增步长为2，也即第一位始终是1
    for (int i = 1; i < 1 << n; i += 2)
        for (int j = 0; j < n; j ++ )
            if (i >> j & 1)
                for (int k = 0; k < n; k ++ )
                    if (i >> k & 1)
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + d[k][j]);
                        
    cout << f[(1 << n) - 1][n - 1] << endl;
    
    return 0;
}

但是这里有一个情况需要考虑：如果迭代时$k=j$会怎样。不妨看看，这时候划分成的小集合是$f[i-(1<<j)][j]$，第一维保证路径中不含点$j$，但是第二维说明路径最后一个点是$j$，明显不合法了，那么它在递推过程中一定始终为无穷大。

分析一下时间复杂度：状态数大概是2²⁰×20，状态转移计算量是20，总时间复杂度差不多是4×10⁸，本题限制是5s，合法。

3、总结

状态压缩dp主要就是怎么把某个状态用位表示出来，以及进行位运算，其中的思路可能比较难思考，但是一旦思路想明白，题很快就能解出。状压dp的标志一般是：数据范围较小，因为要对2进行幂运算，如果数据范围较大，那就不适合用状压了。