【离散数学】图论

图的基本概念

• 无序结点对： 结点对和次序无关
  

• 有序结点对： 结点对和次序有关
  

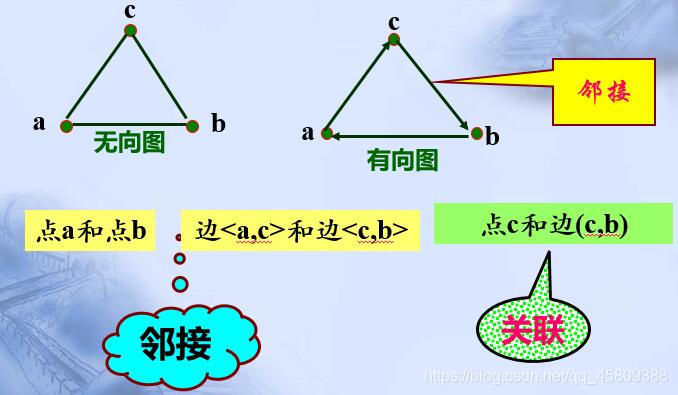
• 邻接 邻接是点与点或者边与边之间的关系。在无向图中，如果两个点之间至少有一条边相连，则称这两个点是邻接的。同样，如果两条边有共同的顶点，则两条边也是邻接的。

• 关联： 关联是点与边之间的关系。一个点如果是一条边的顶点之一，则称为该点与该边关联
  

• 悬挂点： 度数为1的点

• 孤立点： 度数为0的点

• 自环，自回路

顶点的度

在无向图中，指与该顶点相关联的边的条数。

• 偶度顶点： 度数为偶数的顶点
  奇度顶点： 度数为奇数的顶点
• 入度： 以结点v为终点的边数 $d_i(v)$ input
  出度： 以结点v为起点的边数 $d_o(v)$ output
  $d(v)$=$d_i(v)$+$d_o(v)$
• 有向图中，某个顶点有自环，则该顶点的出度和入度分别加1

图的分类

• 有向图： 图中的所有边均为有向边。
• 无向图： 图中的所有边均为无向边。
• 多重图： 含有平行边的图
• 简单图： 不含有自环和平行边的图
• 有限图： 顶点集和边集均为有限集的图

子图

• 子图： 图G’中的点集和边集为图G的子集（G’=<V’，E‘>，G=<V,E>且V’$\subseteq$V,E’$\subseteq$E）G’为G的子图
• 真子图： 图G’中的点集和边集为图G的子集（G’=<V’，E‘>，G=<V,E>且V’$\subseteq$V,E’$\subset$E）G’为G的子图
• 生成子图： 图G’中的点集与G相等，边集为G的子集（G’=<V’，E‘>，G=<V,E>且V’=V,G’$\subseteq$G）G’为G的生成子图

(n,m)图

• (n,m)图： 一个具有n个结点（阶）、m条边所组成的图。
• 零图： (n,0)一个没有边的图
• 平凡图： (1,0)只有一个点的图
• 空图： 顶点集和边集均为空

完全图

• 无向完全图： 无向简单图G (n,m) ，如果其n个结点中的每一个均与其余n-1个结点邻接。
  边数m=$\frac{n(n-1)}{2}$
  
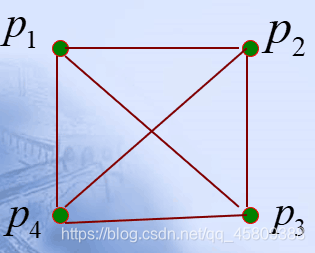
• 有向完全图： 有向简单图G (n,m) ， 如果其n个结点中的每一个均与其余n-1个结点邻接。
  边数m=n(n-1)

补图

G的补图是由G的所有顶点和为了使G成为完全图所需要添加的那些边所组成的图。

d次正则图

每个顶点均有相同度d的图。

• n阶零图是0次正则图
• n个顶点的完全图是(n-1)次正则图。

定理 8.1

设$G=（V,E）$,${\sum }_{v\in V}^{}d(v)=2|E|$

• 度数和必为偶数
• 任何(n,m)图中奇度顶点必为偶数个。

图的表示方法

• 定义描述法： 用点的集合和边的集合来表示
• 图形表示法： 用小圆圈——顶点；线段——边
• 矩阵表示法： 用二进制的数{0，1}表示图中点与点、点与边的关系

有权图

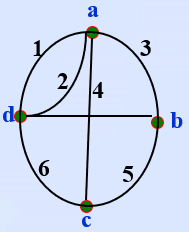
• 权： 附在边旁说明某种信息的数据
• 有权边(带权边)： 带有权的边
• 有权图(带权图)： 图中的边均是有权边之图

通路 回路 连通图

通路

• 简单通路： 若通路中的所有边互不相同称为简单通路
• 基本通路： 若通路中的所有顶点互不相同称为基本通路。
• 基本通路一定是简单通路
• 完备通路： 该通路既是简单回路，又是基本回路

回路

• 基本回路： 若回路长度大于等于3，且所有顶点除了起点和终点是相同点外，没有其他相同顶点在回路中出现。
  

短程

短程（距离）：两个顶点间有若干条通路，必有一条长度最短（经过的边最少）

定理 8.2

一个有向(n,m)图中任何基本通路长度不超过(n-1)，而任何基本回路长度均不超过n。

连通图

可达

设$G=<V,E>$, P,Q是两个顶点 ，若存在一条从P到Q的通路，则称P到Q是可达的

无向图连通

一个无向图G，如果它的任何两结点间均是可达的，则称图G为连通图；否则，称为非连通图。

有向图连通

一个有向连通图G，

• 弱连通： 如果忽略边的方向后其无向图是连通的
• 单向连通： 如果其任何两点间至少存在一向是可达的
• 强连通： 如果其任何两点间均是互相可达的
  

三者关系

• 强连通一定是弱连通，一定是单向连通
• 单向连通一定是弱连通

强连通判定
一个有向图D是强连通 $\leftrightarrow$ D中有一个回路，它至少包含每个顶点一次

图的矩阵表示

邻接矩阵

描述结点与结点之间的关系
$a=(a_{ij}{)}_{n\ast n}$
$M_{ij}=\{\begin{array}{l}1v_i与v_j是邻接的\\ 0\end{array}$

无向图

• 无向图的邻接矩阵是对称的
• 每行元素之和恰好为该顶点的度
• 所有元素之和等于2m
  

有向图

• 有向图的邻接矩阵一般是不对称的
  

• 求一个有向图某点的度数：入度+出度
  将该点对应的行列布尔数相加，分别即为出度和入度的度数
  $d_o(v_i)={\sum }_{k=1}^n{a}_{ik}$
  $d_i(v_i)={\sum }_{k=1}^n{a}_{ki}$
  $d(v_i)=d_o(v_i)+d_i(v_i)$

  $A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$
  2的度数=（0+0+0+1）+（1+0+1+0）=3

特殊矩阵

• 若邻接矩阵的元素全为零，则对应的图是零图。
• 若邻接矩阵除主对角线元素为0，其他全为1,则对应的图是连通的且为简单完全图。

定理 8.3（矩阵相乘）

设邻接矩阵为A的无向简单图，则$A^k$(k=1,2,3…)的元素是连接$v_i$到$v_j$的长度为k的通路的总数，而$a_{ii}^k$为$v_i$到$v_i$长度为k的回路总数。

可达矩阵

$M_{ij}=\{\begin{array}{l}1v_i与v_j是可达的\\ 0\end{array}$

连通矩阵

对无向图G, n阶方阵C称为G的连通矩阵

可达矩阵

对有向图D, n阶方阵C称为可达矩阵

求可达矩阵方法

法一： A为邻接矩阵 $P=A+A^2+A^3+...+A^n$
法二： 邻接矩阵A当作关系矩阵，求连通矩阵就相当于求A的传递闭包。 $t®=U_{i=1}^\infty =R\cup R^2\cup R^3\cup…\cup R^n\$

关联矩阵

无向图

对于无自环的无向图G，其关联矩阵$M_G=(a_{ij}{)}_{n\ast m}$
$M_{ij}=\{\begin{array}{l}1v_i与e_j是关联的\\ 0\end{array}$

• 关联矩阵中每列包含两个1；（一个边必和两个点关联）
• 每行元素之和等于该顶点的度；
• 一行元素全为0，对应的顶点为孤立点

有向图

$M_{ij}=\{\begin{array}{l}1v_i是e_j的起点\\ -1v_i是e_j的终点\\ 0\end{array}$

• 关联矩阵中每列包含两个1；
• 每行中1的个数为该点的出度，-1的个数即为该点的入度
• 一行元素全为0，对应的顶点为孤立点