离散数学——图论

最新推荐文章于 2024-05-23 20:37:36 发布

番茄元

最新推荐文章于 2024-05-23 20:37:36 发布

阅读量2.3k

点赞数 2

分类专栏：基础知识文章标签： python 概率论机器学习

本文链接：https://blog.csdn.net/zhiai_/article/details/117093918

版权

基础知识专栏收录该内容

8 篇文章 5 订阅

订阅专栏

图论

一、图的基本理论
- - - - 握手定理：每条边对顶点的度的贡献为2
二、连通图、补图、偶图
- 补图
- 双图
欧拉图
- 欧拉闭迹：包含所有顶点所有边的闭迹。每个边只经过一次，但是顶点可以重复经过。
- 欧拉图：包含欧拉闭迹的图。
- 多重图
哈密顿图
- 染色法：判断图不是哈密顿图
图的表示：邻接矩阵
- 带权图：
- - 相关问题
三、树
连通度、匹配
- - - 明格尔定理
    - 柯尼希定理
- 图的种类
- - 网络流：（流的集合）带有边权值的有向图。
- 匹配问题
- 相异代表系
平面图
- 顶点着色
- 图的着色
- 四色定理
- 五色定理
有向图
- - 度
  - 同构（NP完全问题，是个难问题）
- 有向路，有向圈
- 邻接矩阵
有向树、有根树
- - 有序树
- 完全二元树
- 比赛图

一、图的基本理论

无向图 G=(V,E); 反自反 + 对称
有向图 D=(V,A);
邻接矩阵用布尔矩阵表示图
子图
G的生成子图：包含G所有顶点的子图
顶点的度

握手定理：每条边对顶点的度的贡献为2

在这里插入图片描述
r-正则图：每个点的度都为 r

完全图： p-1 正则图
双图： m个顶点之间无顶点 n个顶点之间无顶点 m,n之间有顶点
双图完全图： m与n间每个顶点连边

例题：（反证）假设每个人朋友数都不相同，每个人的朋友数为0，1，2，…，N-1
N-1与所有人是朋友，0与所有人都不是朋友，矛盾
在这里插入图片描述
同构：存在两个图，图之间的点一一对应（双射），对应边相同
以下顶点名称交换，图不同，图同构

同构的判断：去掉某个顶点，子图同构

二、连通图、补图、偶图

通道：顶点和边的交错序列
迹：没有重复的边的通道
闭迹：
路：没有重复顶点的通道
圈：闭路
连通图：任意两个顶点之间有路（闭包）
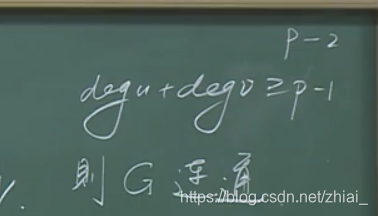
在这里插入图片描述

此处为向上取整

v,u等价：v,u之间有路（划分）
图的划分：利用导出子图：极大连通子图 == 支（没有子图能包含它）
（包含关系是偏序关系不能说最大）

证明方法

1.演绎法：
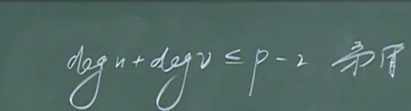
在这里插入图片描述

2.反证法：
假设至少有两个支…
3.数学归纳法：

判定是否有圈

图中每个顶点的度均为偶数，且存在顶点的度不为0.

常用方法：最长路法

在这里插入图片描述
上证中：若v1的邻接点不在 1~n 则与最长路矛盾。
最小度 >= m 则有长 >= m+1 的圈。
E.G：圆桌吃饭问题：让每个人左右都是自己认识的朋友。

如果两个顶点之间有两条不同的路，则图中有圈。
证明：利用子图 + 或 - 边（顶点）后仍然连同即证
在这里插入图片描述

补图

G的补图 == 将E 变为 顶点的二元子集 差 E

两个图同构，那么两个图的补图同构
自补图：图与其补图同构
E.G：在这里插入图片描述
问题转化为证明，图中有三角形

很难求！

双图

V有一个而划分，每条边的两个顶点分居两个划分中。
双图无向图中，圈的长度为偶数（那双图中肯定就没有三角形啦）

欧拉图

欧拉闭迹：包含所有顶点所有边的闭迹。每个边只经过一次，但是顶点可以重复经过。

欧拉图：包含欧拉闭迹的图。

G是欧拉图
《=》 G是连通的，且每个顶点的度都是偶数
在这里插入图片描述

多重图

多重图：

两个顶点之间有多条边

带环图：

顶点与自身有边。（不满足反自反）

伪图：

多重图与带环图共同构成（由于图需要满足反自反）

欧拉定理：

有一条欧拉迹《=》图中恰有两个奇度顶点
G中有 2n 个奇度顶点《=》 G中至少有 n 条《=》 n 笔画完

哈密顿图

染色法：判断图不是哈密顿图

相邻顶点染不同色（共两种），能完成染色，且两种颜色的顶点数不同，则不是哈密顿图。
注意： 如为五边形，不能染色，但是是哈密顿图。（边加细，加顶点）
	   如四个顶点的一条线，能染，但不是哈密顿图。

=》去掉|S|个顶点，产生的支少于|S|，则为哈密顿图。（利用去顶点的破圈法）
在这里插入图片描述

=》
在这里插入图片描述
证明：（证明其逆否命题成立）假设满足条件是图不是哈密顿图，。给不邻接的顶点之间加边，直到形成哈密顿圈，去掉最后一条边，得到一条哈密顿路。

否则形成哈密顿圈。

两个不相邻的顶点度之和 >= p 是哈密顿图
两个不相邻的顶点度之和 >= p-1 有哈密顿路（证明最长路法，发现有一个一个圈和孤立点，不是哈密顿图）
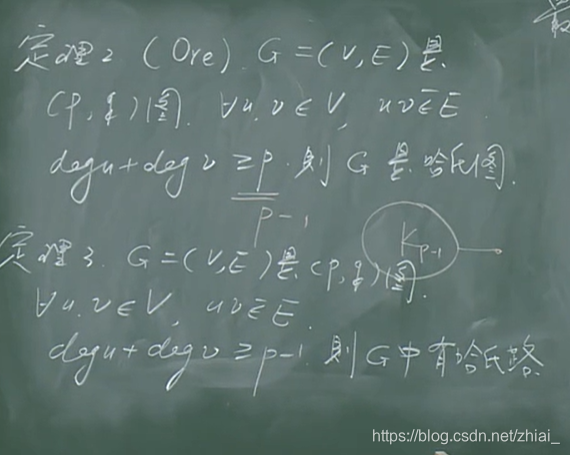
在这里插入图片描述

图的表示：邻接矩阵

邻接矩阵B（01）存图，B^l （i，j）位置的数字表示从	vi - > vj 的，长度为 l 的路有多少条。
证明：数学归纳法

邻接表：利用指针。
在这里插入图片描述
关联矩阵：顶点和边对应
每一列 2 个 1

图解：用于分析数据与问题的图模型

带权图：

f 对应顶点信息     g 映射边权

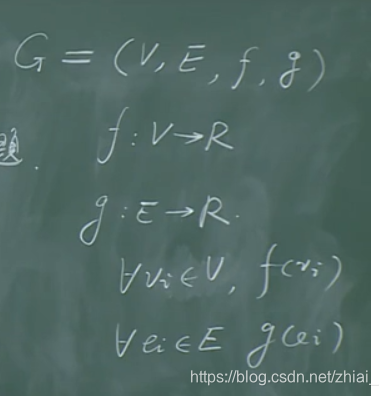
在这里插入图片描述

欧拉图与哈密顿图有什么区别？边遍历和点遍历的区别。欧拉回路是指不重复地走过所有路径的回路，而哈密顿回路是指不重复地走过所有的点并且最后还能回到起点的回路。具有欧拉回路的图是欧拉图，具有哈密顿回路的图是哈密顿图。

三、树

定义：连通的无圈的图
结点的度：一个结点含有的子结点的个数称为该结点的度。
节点的度：结点拥有的子树数目称为结点的度，叶子结点就是度为0的结点
树的度：树内各结点的度的最大值
分支节点：度不为0的节点
平凡树：只有一个顶点的图
叶子：度为 1 的顶点
非平凡树：至少 2 个叶子
树是双图：可以用染色法，color1 染所有叶子，去掉所有叶子， color2 再染所有叶子
森林：没有圈的图
Δ(G)：顶点的最大度

五个等价定义

在这里插入图片描述

极小连通图

定义： 去掉一条边则不连通
G是树 《=》 G 是极小连通图

连通分量无向图G的极大连通子图称为G的连通分量（Connected Component）。
任何连通图（任意两个顶点之间可达的图）都只有一个连通分量，即自身，非连通图有多个连通分量。

树的中心

e(v) : 偏心率： u,v之间的最大距离
r（G）：树的半径：最小偏心率
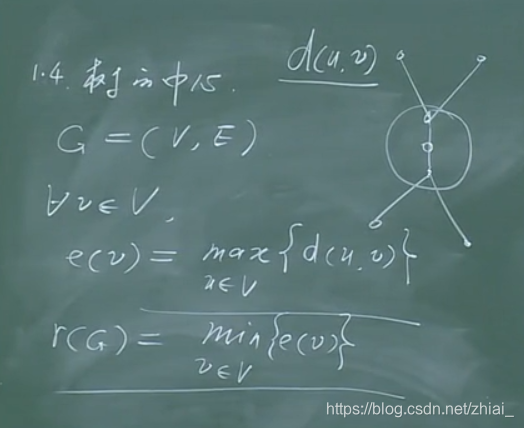
在这里插入图片描述
中心v ： e(v) = r(G)
找树的中心：
法一：不停的去树周的页子，直到只剩 1 个或 2 个顶点
法二：找最长路的中间点

生成树

G的生成子图如果是树，则称生成树
G有生成树《=》 G 是连通的（证明：破圈法）
在这里插入图片描述
基尔霍夫矩阵（两种求法）
B 关联矩阵
D 是顶点的度数矩阵（只有对角线有值） B 邻接矩阵
生成树的个数：行列式主子式的绝对值

最小生成树

在这里插入图片描述
两种算法：

Prim : 从一个顶点出发去找与其相连的边权最小的顶点相连（注意判圈），直到所有顶点加入（更适用于稠密图）
Kruscal ：不断选取图中边权值最小的边（注意判圈），直到图连同

割点、桥

割点：去掉割点后图的支数增加
1.每个非平凡的图，至少有两个顶点不是割点。
2.有割点的图不是哈密顿图。

桥：与割点定义相似， v --》x
有桥的图一定不是哈密顿图，因为桥的两个顶点不在一个圈里，不能每个点只经过一次还能返回。

在这里插入图片描述
等价闭包：自反、传递、对称闭包。

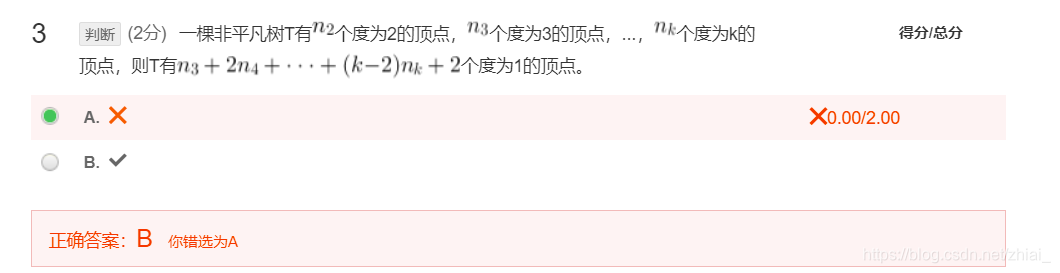
连通度、匹配

连通度：要使图变为平凡图或者不连通，所需要去掉的最少顶点（边）数，称为顶点（边）连通度。
在这里插入图片描述
最小度也能反映连通程度：（k(G) 拉姆达G）更精确）

在这里插入图片描述

n-连通图：K（G）》= n
独立轨：任意两个顶点之间不相交的路
最大最小问题：独立轨的最大、最小值能反映图的连通度

明格尔定理

在这里插入图片描述
门格尔：分离s,t所需要的最少顶点数等于s，t 间不相交的路（独立轨）的最大条数。
最大流最小截 =》明格尔
明格尔 =》最大流最小截（割）

柯尼希定理

在这里插入图片描述

图的种类

完全图： 图中的每个顶点都与其他的所有顶点相连。
正则图： 图中每个顶点的度相同且为 k ， 称为 k- 正则图。
二部图（偶图、二分图）：顶点分为 V1 和 V2 两个点集，图中的每条边两端分别连在 V1 、V2 的端点上。
完全二部图： V1 中的每个顶点和 V2 中的每个顶点分别相连。

网络流：（流的集合）带有边权值的有向图。

可行流：不超过管道容量
零流：容量减去流量 = = 0
流量：
伪流：满足
最大流：最大可行流
饱和弧：流量的容量
链：不考虑方向的路
增广路：满足以下条件的链：1.前向弧不饱和 2.后向弧不是0
残留流量：容量 - 实际流
残留网络：弧上标残余流量
割：割边（去掉边后不连通）
最小割：
割的容量：边的集合
增广路定理：容量网络中一个可行流是最大流《=》不存在增广路
最大流、最小割定理：最大流 = = 最小割

所谓网络或容量网络指的是一个连通的赋权有向图 D= （V、E、C），其中V 是该图的顶点集，E是有向边(即弧)集，C是弧上的容量。此外顶点集中包括一个起点和一个终点。网络上的流就是由起点流向终点的可行流，这是定义在网络上的非负函数，它一方面受到容量的限制，另一方面除去起点和终点以外，在所有中途点要求保持流入量和流出量是平衡的。如果把下图看作一个公路网，顶点v1…v6表示6座城镇，每条边上的权数表示两城镇间的公路长度。现在要问：若从起点v1将物资运送到终点v6去，应选择那条路线才能使总运输距离最短?这样一类问题称为最短路问题。如果把上图看作一个输油管道网， v1 表示发送点，v6表示接收点，其他点表示中转站，各边的权数表示该段管道的最大输送量。现在要问怎样安排输油线路才能使从v1到v6的总运输量为最大。这样的问题称为最大流问题。

匹配问题

独立集：互相之间没有连边的点的集合
最大独立集：求~ NPC问题（没有好算法）
团：互相之间有连边的点的集合
匹配：边独立集
边独立集：边与边之间没有公共顶点的边的集合

匹配：

在图论中，一个图是一个匹配（或称独立边集）是指这个图之中，任意两条边都没有公共的顶点。
这时每个顶点都至多连出一条边，而每一条边都将一对顶点相匹配。

偶图匹配问题：
在这里插入图片描述
经典问题：结婚问题

匹配：点覆盖

点覆盖：每条边都被顶点覆盖
最小点覆盖：
边覆盖集：每个顶点都被边覆盖
最小边覆盖集：
支配集：第一个支中的顶点与第二支中的顶点连边（类似于支配者支配被支配者）如下图
在这里插入图片描述

二分图的性质

在这里插入图片描述
最大匹配数：最大匹配的匹配边的数目
最小点覆盖：选取最少的点使任意一条边至少被一个点覆盖
最小边覆盖
最大独立集

相异代表系

每个姑娘Xi 中意的小伙子构成的集合为T(xi)，从每个T中取出一个不相同的元素（小伙子）组成S集合，S称为X 的相异代表系
在这里插入图片描述

相异代表系S 是个集合，无序

平面图

顶点着色

平面图
可平面图

图是已经画在一个平面上且各边除顶点外不相交的图，可平面图是可以画在一个平面上且各边除顶点外不相交的图。

面：

内部面：
外部面：给一个图必有外部面
圈长：
围长：最小圈长
欧拉公式： p - q + f = 2 (平面图满足)

在这里插入图片描述

分析：方法二：先证明该多面体每个面的边数为3，再利用欧拉公式证明顶点数不为整数，即证。

K5 K6 K7 超过5 的完全图都不可平面化

完全图是每对顶点之间都恰连有一条边的 简单图 。
n 个端点的完全图有 n 个端点及 n (n − 1) / 2条边，以 Kn 表示。 它是 (k − 1)- 正则图 。

在这里插入图片描述
上图条件为充分非必要条件

在这里插入图片描述

哭了，孩子除了目测没别的办法了
注意： T6 中可以拆解出多个可平面化的支

二分图的圈最小是4 ， q 《= 2*p - 4
在这里插入图片描述

同胚：
边加细：增加2度顶点
边收缩：将相邻两边合为一个

能够由K3 K5通过边加细或者边收缩得到的图不使平面图

图的着色

色数：涂完整张图所需的顶点数（C 表示圈）
在这里插入图片描述

下界：图中与v不相邻的点的个数为 p - delt(G) -1，则一般情况下，至多有 p - delt(G) 个同色的顶点，色数 * 最大同色顶点数》= 顶点数
上界：（数学归纳法）
去掉这个顶点，归纳假设剩下的顶点均Δ(G) +1 可着色（而 v 周围的顶点仅用了Δ(G)）种颜色。
对刚才去掉的顶点，用另外的一种颜色着色即可。

若G 是平面图则 G 是Δ(G) 可着色的。

在这里插入图片描述
可平面图是6-可着色的。因为可平面图最小度《= 5
归纳假设去掉该顶点是 6- 可着色的，加上该顶点仍然满足。

四色定理

用计算机算了 1200 h,得证

五色定理

由一高中生证明：
施归纳于p ，假设有 p 个顶点时满足五色定理，往证 p+1 个顶点时成立
在这里插入图片描述

分类讨论由 v1 v3导出的子图中，同支与不同支的情况

不同支，v1 所在支中染c1 c3 色的颜色互换，最终余出来一种颜色给 v
同支时，则v2 v4 同支，重复上述操作
即证。
MOOC:

图中X 应为 delt ，是下届定理。

3.如果图 G = (V, E) 是⼀个连通且不完全图，也不是奇数⻓度的圈, 则 G是 ∆(G) （最大度）可着⾊的。如果图G为圈，则图G的色数为2。（✖）需要条件偶圈

有向图

D（V,E）表示有向图

图的表示方法：
1.定义
2.图像
3.邻接矩阵（两个轴都是顶点）
4.关联矩阵（记录顶点对应的边数）

p 个顶点的无向图的个数： p个顶点的二元子集
在这里插入图片描述
p 个顶点的有向图的个数：去掉每个顶点与自己的连边

有 q 条边的有向图的个数：从p 个顶点的有向图中取q 条边

伪图：（多重弧与带环图）

定向图：单行道

度

在这里插入图片描述

有向图补图： V*V 去掉（v,v），再去掉 A，得到 A 的补

同构（NP完全问题，是个难问题）

具体问题具体分析，对于复杂的图可以分解着来
在这里插入图片描述

有向路，有向圈

有向图强连通分量：在有向图 G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通 (strongly connected)。
.
如果有向图G的每两个顶点都强连通，称G是一个强连通图。
.
有向图的极大强连通子图，称为强连通分量 (strongly connected components)。.

可达

u，v 之间有路

连通性

弱连通：（有一条弱路）u，v 之间有一条不考虑方向的路
单向连通：每两个点之间单向连同
强连通：（互达）
在这里插入图片描述

强支

R 自反（顶点之间互达）、对称、传递
即等价关系
即存在划分（V/R V 对R 的商集，商集求出的正好是等价关系的等价类，这些等价类构成的集合是V 的一个划分）

Vi 的导出子图包括Vi 的所有顶点和所有在 E 中的边
每个与Vi 中任何一个顶点等价的顶点都在其中，称为强支
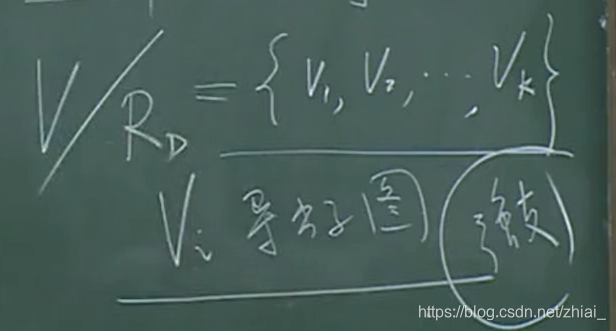
在这里插入图片描述

应用

DAG：有向无环图
拓扑排序：后面的顶点依赖于前面的顶点，而不会出现前面的顶点依赖后面顶点的情况
OS 操作系统（出现强支（互达）死锁）
交通控制：
有一个无向图，只要该图没有桥，则一定存在一个有向图是强连通的
（适用于小规模）

邻接矩阵

1.求通道数
类似闭包，算步数 ==》求通道条数
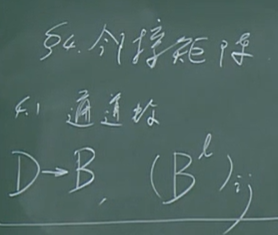
在这里插入图片描述
2. 可达矩阵
自己与自己之间有路 I ，有一条路B 有两条路 B^2 …

3. 求强支

MOOC:

有向树、有根树

在这里插入图片描述

有序树

序在兄弟节点之间
层、深度、高度： 0 1 2 3 …
满 m-正则树（每层 2^层数那么多节点）
在这里插入图片描述
DEG 优化，消除子表达式

完全二元树

最后一曾未必满，但是全部靠左
在这里插入图片描述
堆：（特殊的完全二元树）有序，小根堆，大根堆

比赛图

找哈密顿路，先找 p 个顶点的，在和最后一个顶点分别比赛，建立输赢对应的边，找最后一条指赢边，构成 p+1 个顶点的哈密顿路。
在这里插入图片描述
I 是叶的深度总和， E 是内顶点的深度之和， i 内节点数

归纳法

番茄元

关注

2
点赞
踩
28

收藏

觉得还不错? 一键收藏
0
评论
离散数学——图论

无向图 G=(V,E); 反自反 + 对称有向图 D=(V,A);邻接矩阵用布尔矩阵表示图子图G的生成子图：包含G所有顶点的子图顶点的度握手定理：每条边对顶点的度的贡献为2r-正则图：每个点的度都为 r完全图： p-1 正则图双图： m个顶点之间无顶点 n个顶点之间无顶点 m,n之间有顶点双图完全图： m与n间每个顶点连边例题：（反证）假设每个人朋友数都不相同，每个人的朋友数为0，1，2，…，N-1N-1与所有人是朋友，0与所有人都不是朋友，矛盾同构：...
复制链接

扫一扫