算法导论复习

算法概述

算法的概念

一系列将问题的输入转换为输出的计算或操作步骤。

算法设计思想:尽量选择复杂度低的算法，选择合适的数据结构，考虑时间空间权衡和实现成本的权衡。

算法的性质

输入，有外部提供的量作为算法的输入。

输出，算法产生至少一个量作为输出

确定性，组成算法的每条指令是清晰、无歧义的

有限性，算法中每条指令的执行次数是有限的，执行每条指令的时间也是有限的。

算法描述语言

自然语言、流程图、程序设计语言、伪代码。

算法复杂性分析

主要考虑时间复杂性： $T=T(N,I)={\sum }_{i=1}^k{t}_i{e}_i(N,I)$

$k$ 是元运算的种类，$t_i$是元运算时间，$e_i(N,I)$是元运算次数，与规模 $N$ 和输入 $I$ 有关。

渐进性态的阶

大O表示法（算法运行时间的上界）

若存在正常数 $C$ 和自然数 $N_0$ 使得当 $N\ge N_0$时，有$f(N)\le Cg(N)$，则称函数 $f(N)$在 $N$充分大时有上界，且 $g(N)$ 是它的一个上界，记为 $f(N)=O(g(N))$，也称 $f(N)$ 的阶不高于 $g(N)$ 的阶。上界的阶越低则评估越精确。

大Ω表示法（算法运行时间的下界）

若存在正常数 $C$ 和自然数 $N_0$ 使得当 $N\ge N_0$时，有$f(N)\ge Cg(N)$，则称函数 $f(N)$在 $N$充分大时有下界，且 $g(N)$ 是它的一个下界，记为 $f(N)=\Omega (g(N))$，也称 $f(N)$ 的阶不低于 $g(N)$ 的阶。下界的阶越高评估越精确。

θ表示法（算法运行时间接近的界）

$f(N)=\theta (g(N))$ 当且仅当$f(N)=O(g(N))$ 且$f(N)=\Omega (g(N))$ ，称函数$f(N)和g(N)$ 同阶。

常见的阶：

$O(1)<O(logn)<O(N)<O(N^c)<O(c^N)<O(N!)<O(n^n)$

常数级<对数级<线性级<多项式级<指数级<阶乘级<$n^n$级

NP完全性理论

在多项式时间内能求出结果的为P(Polynomial)问题，在多项式时间内能验证猜测解的正确性，为NP(Nondeterministic Polynomial)问题。NP问题不要求给出一个算法来求解问题本身,而只要求给出一个确定性算法在多项式时间内验证它的解。

递归与分治

递归设计的思想

递归函数是用函数自身定义的函数，它的两个要素是边界条件与递归方程。递归算法是自身调用自身的算法。下面是一个例子。

$$F(n)=\{\begin{array}{ll}1& n=0\\ 1& n=1\\ F(n-1)+F(n-2)& n>1\end{array}$$

int fibonacci(int n)
   {
       if (n <= 1) return 1;
       return fibonacci(n-1)+fibonacci(n-2);
   }

递归函数的优点：
1)算法简明；
2)正确性易证明，是分析、设计的有力工具。

递归函数的缺点：
执行效率不高；
堆栈空间耗费

汉诺塔问题

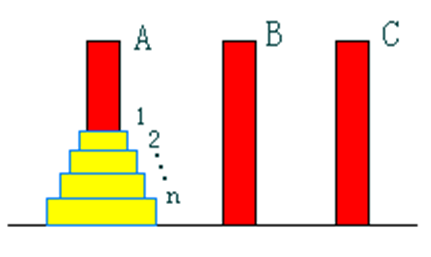
问题描述：

设a,b,c是3个塔座。在塔座a上有一叠共n个圆盘，这些圆盘自下而上，由大到小地叠在一起。各圆盘从小到大编号为1,2,…,n,现要求将塔座a上的这一叠圆盘移到塔座b上，并仍按同样顺序叠置。在移动圆盘时应遵守以下移动规则：规则1：每次只能移动1个圆盘；规则2：任何时刻都不允许将较大的圆盘压在较小的圆盘之上；规则3：在满足移动规则1和2的前提下，可将圆盘移至a,b,c中任一塔座上。

算法思想1：

这个问题有一个简单的解法。假设塔座a、b、c排成一个三角形，a→b→c→a构成一顺时针循环。在移动圆盘的过程中，若是奇数次移动，则将最小的圆盘移到顺时针方向的下一塔座上;若是偶数次移动，则保持最小的圆盘不动，而在其他两个塔座之间，将较小的圆盘移到另一塔座上去。

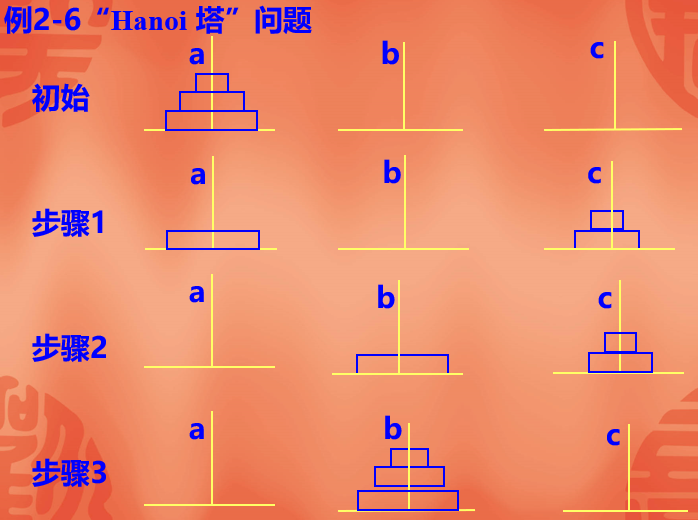
递归算法思想：

下面用递归技术来解决这个问题。当n=1时，问题比较简单。此时，只要将编号为1的圆盘从塔座a直接移至塔座b上即可。当n>1时，需要利用塔座c作为辅助塔座。此时要设法将n-1个较小的圆盘依照移动规则从塔座a移至塔座c上，然后将剩下的最大圆盘从塔座a移至塔座b上,最后设法将n-1个较小的圆盘依照移动规则从塔座c移至塔座b上。由此可见，n个圆盘的移动问题就可分解为两次n-1个圆盘的移动问题，这又可以递归地用上述方法来做。

算法复杂性：

$$\begin{array}{rl}T(n)& =\{\begin{array}{ll}2T(n-1)+1& n>2\\ 1& n=1\end{array}\\ T(n)& =2T(n-1)+1=2(2T(n-2))\\ & =2^{2}T(n-2)+2+1\\ & =2^{3}T(n-3)+2^2+2+1\\ & =2^{n-1}T(1)+2^{n-2}+...+2+1\\ & =\frac{2^{n-1}-1\ast \frac{1}{2}}{1-\frac{1}{2}}\\ & =2^n-1\\ & 故该算法的时间复杂度为O（2^n）\end{array}$$

代码：

void hanoi(int n, int a, int b, int c){
  if(n>0){
    hanoi(n-1,a,c,b);
    move(a,b);
  hanoi(n-1,c,b,a);
  }
}

其中，hanoi(n, a,b, c)表示将塔座a上自下而上，由大到小叠放在一起的n个圆盘依移动规则移至塔座b上并仍按同样顺序叠放。在移动过程中，以塔座c作为辅助塔座。move(a，b)表示将塔座a上编号为n的圆盘移至塔座b上。

分治法的设计思想

将规模为n的问题分解为k个规模较小的子问题,使这些子问题相互独立且与原问题相同，递归地解这些子问题，然后各个子问题的解合并得到原问题的解。

分治法所能解决的问题一般具有以下特征:

该问题可以分解为若干个规模较小的相同问题；
该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题；
该问题的规模缩小到一定的程度就可以容易地解决；
利用该问题分解出的子问题的解可以合并为该问题的解。

分治法的求解过程

(1)分解：把原问题分解为若干个规模较小、相互独立，
与原问题相同的子问题；

(2)求解：若子问题规模较小且容易被解决则直接解，
否则再继续分解为更小的子问题，直到容易解决；

(3)合并：将已求解的各个子问题的解，逐步合并
为原问题的解。

二分搜索

问题描述：

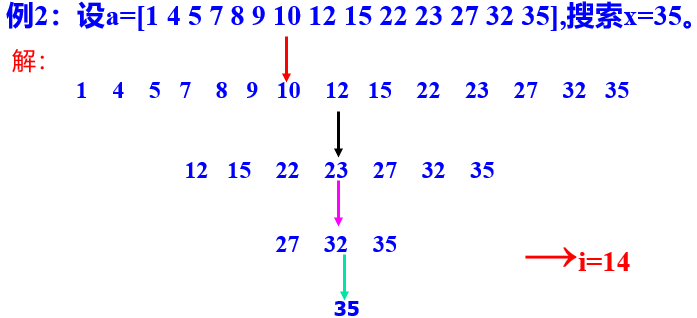
给定已按升序排好序的n个元素a[0:n-1]，现要在这n个元素中找出一特定元素x。

算法思想：

将n个元素分成个数大致相同的两半，取$a_{mid}$与x作比较。

$x=a_{mid}$ 则算法中止

$x<a_{mid}$ 在数组的左半部继续搜索

$x>a_{mid}$ 在数组的右半部继续搜索

分治过程：
$$T（n）\to T（\frac{n}{2}）\to T（\frac{n}{4}）\to \cdots \to T（\frac{n}{2^k}）=T(1)$$
时间复杂性：
$$\begin{array}{rl}T(n)& =\{\begin{array}{ll}1& n=1\\ 1+T(\frac{n}{2})& n>1\end{array}\\ & \\ T(n)& =T(\frac{n}{2})+1=T(\frac{n}{2^2})+1+1\\ & =T(\frac{n}{2^2})+2=T(\frac{n}{2^3})+1+2\\ & =T(\frac{n}{2^3})+3=T(\frac{n}{2^k})+k\\ & 令n=2^k则k=logn则T(\frac{n}{2^k})+k=T(1)+k=1+logn\\ & 故二分搜索算法的时间复杂度为O（logn）\end{array}$$

代码：

template<class Type>
int BinarySearch(Type a[ ], const Type & x, int n){//在a[0]<=a[1]<=...<=a[n-1]中搜素x
    //找到x时返回其在数组中的位置，否则返回-1
    int left = 0;	int right = n-1;			         
        while(left <= right){ 
            int middle=(left+right)/2;                  
 	        if (x = = a[middle] 
               return middle;
            if (x > a[middle])  
               left = middle + 1;
            else 
                right = middle – 1;			                     
        }
        return -1 //未找到			                       
}

合并排序

问题描述：

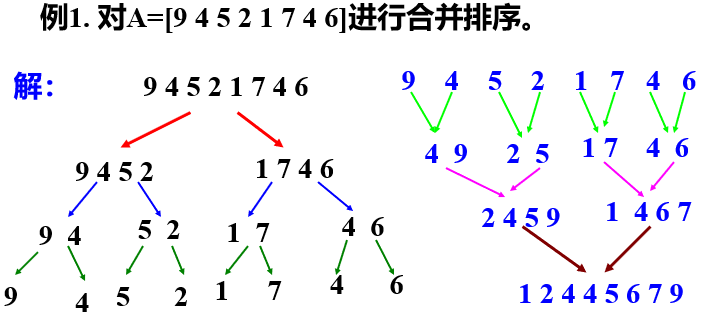
合并排序算法是用分治策略实现对n个元素进行排序的算法。

算法思想：

将待排序元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排好序的子集合合并成所要求的排好序的集合。

时间复杂性：
$$\begin{array}{rl}T(n)& =\{\begin{array}{ll}O(1)& n=1\\ 2T(\frac{n}{2})+O(n)& n>1\end{array}\\ & \\ T(n)& =2T(\frac{n}{2})+cn=2(2T(\frac{n}{4})+c\frac{n}{2})+cn\\ & =2^{2}T(\frac{n}{2^2})+2cn\\ & =\cdot \cdot \cdot \\ & =2^{k}T(\frac{n}{2^k})+kcn\\ & 令n=2^k则k=logn则T(n)=2^{k}T(1)+cnlogn=O(nlogn)\\ & 故合并排序算法的时间复杂度为O（nlogn）\end{array}$$
代码：

temlplate  <class type>
void MergeSort(Type a[], int left, int right){   
    if (1eft < right){  //至少有2个元素
       int i = (left + right ) /2; //取中点
       MergeSort(a, 1eft, i)；
       MergeSort(a, i+1, right)；
       Merge(a, b, 1eft, i, right)；//从a合并到数组b
       copy(a, b, left, right);//复制回数组a
     } 
}    

快速排序

问题描述：

快速排序是基于分治策略的另一个排序算法。

算法思想：

对于输入的子数组a[p:r]，按以下三个步骤进行排序。

(1) 分解：以a[p]为基准元素将a[p:r]划分成3段a[p:q-1]， a[q]和a[q+1:r]，使a[p:q-1]中任意一个元素小于等于a[q]，而a[q +1 :r]中任何一个元素大于等于a[q]，下标q在划分过程中确定;

(2) 递归求解：通过递归调用快速排序算法分别对a[p:q-1]和a[q+1:r]进行排序;

(3)合并：对于a[p:q-1]和a[q+1:r]的排序是就地进行的，因此在a[p:q-1]和a[q+1:r]都已排好序后，不需要执行任何计算，a[p:r]则已排好序。

时间复杂度：

快速排序的性能取决于划分的对称性，最坏情况是：每次划分后2个区域的元素为n-1，1
$$\begin{gathered} T_{max}(n)=\{\begin{array}{ll}O(1)& n=1\\ T(n-1)+O(n)& n>1\end{array} \\ {T}_{max}(n)=O（n^2） \end{gathered}$$
最好情况是：每次划分后都产生大小为n/2的两个区域。
$$\begin{gathered} T_{min}(n)=\{\begin{array}{ll}O(1)& n=1\\ 2T(\frac{n}{2})+O(1)& n>1\end{array} \\ {T}_{min}(n)=O（nlogn） \end{gathered}$$
平均情况下时间复杂性也是$O（nlogn）$

代码：

template <class Type>
void QuickSoft(Type a[], int p, int r){  
  if(p<r){
    int q=Partition(a, p, r);
    QuickSort(a, p, q-1); //对左半段排序
    QuickSoft(a, q+1, r); //对右半段排序
  }
}

对含有n个元素的数组a[0:n-1]进行快速排序只要调用QuickSort(a, 0, n-1)即可。上述算法中的函数Partition()以一个确定的基准元素a[p]对子数组 a[p:r]进行划分，它是快速排序算法的关键。

template<class Type>
int Partion(Type a[ ],int p , int r ){  
  int i=p;  j=r+1;
  Type x=a[p];
  //将小于x的元素交换到左边区域，将大于x的元素交换到右边区域
  while(true) { 
    while(a[++i] < x&&i<r);
    while(a[--j] > x);
    if (i>=j ) 
      break;
    swap(a[i],a[j]); 
   }
   a[p] = a[j];
   a[j] = x;
   return j;
}

线性时间选择

问题描述：

给定线性序集中n个元素和一个整数$k(1\le k\le n)$，要求找出这n个元素中第k小的元素。

算法思想：

找到一个支点，对输入数组进行划分为a和b两段，然后计算a部分的元素个数j：

$k\le j$ 第k小元素为a的第k小元

$k>j$ 第k小元素为b的第(k-j)小元

基准点的选取是影响性能的关键。
基准点选取的算法思路（中间的中间）：

(1) 将n个输入元素划分成$\lceil \frac{n}{5}\rceil$个组，每组5个元素，除可能有一个组不是5个元素外。用任意一种排序算法，将每组中的元素排好序，并取出每组的中位数，共$\lceil \frac{n}{5}\rceil$个。
(2) 递归调用Select找出这$\lceil \frac{n}{5}\rceil$个元素的中位数（中位数元素的中位数）。如果$\lceil \frac{n}{5}\rceil$是偶数，就找它的两个中位数中较大的一个。然后以这个元素作为划分基准。

时间复杂性：
$$\begin{gathered} T(n)\le \{\begin{array}{ll}{C}_1& n<75\\ C_{2}n+T(\frac{n}{5})+T(\frac{3n}{4})& n\ge 75\end{array} \\ 分析过程不再给出 \\ 解此递归式可得T(n)=O(n) \end{gathered}$$
代码：

template<class Type>
Type Select(Type a[],int p, int r, int k) {
  if (r-p < 75){
  用某个简单排序算法对数组a[p:r]排序;
  return a[p+k-1];
  }
  for (int i=0; i <= (r-p-4)/5; i++) {
    //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
    Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//找中位数的中位数，r-p-4即上面所说的n-5
    int i = Partition(a, p,r, x),j = i-p+1;
    if (k <= j)
      return select(a,p,i,k);
    else
      return Select(a,i+1,r,k-j);
  }
}

此外还有排列问题、整数划分问题、大整数乘法、棋盘覆盖、最接近点对、循环赛日程表

动态规划

基本概念：

多阶段决策问题：在每一个阶段都要做出决策，全部过程的决策是一个决策序列。把多阶段过程转化为一系列单阶段问题，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。

动态规划(dynamic programming)属运筹学中的规划论分支，是求解决策过程最优化的数学方法。与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合用动态规划求解的问题，经分解得到的子问题往往不是相互独立的。

动态规划的特点：动态规划法用于最优化问题时，这类问题会有多种可能的解，而动态规划要找出其中最优值的解。对于重复出现的子问题，只在第一次遇到时加以求解，并把答案保存起来，以后再遇到时不必重新求解。

动态规划的基本要素：

(1) 最优子结构

原问题的最优解包含其子问题的最优解。

(2) 重叠子问题

在用递归算法自顶向下解某类问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算。利用这种子问题重叠的性质,对每一个子问题只解一次,而后将其解保存在一个表格中，当再次需要解此子问题时只是简单地用常数时间查看一下结果。(迭代)

动态规划的实质是分治思想和解决冗余：

(1) 一种将问题实例分解为更小的、相似的子问题。

(2) 存储子问题的解而避免计算重复的子问题。

一般来说，只要原问题可以划分成规模更小的子问题，并且原问题的最优解中包含了子问题的最优解（即满足最优化原理），则可以考虑用动态规划解决。

动态规划算法设计步骤：

⑴分析最优解的性质，并刻划其结构特征；

⑵递归地定义最优值；

⑶以自底向上的方式计算出最优值；

⑷根据递归计算最优值时得到的信息，从子问题的最优解逐步构造出整个问题的最优解。

矩阵连乘

问题描述：

给定n个矩阵{ $A_1,A_2,..A_n$}其中$A_i$ 与$A_{i+1}$ 是可乘的（i=1,2,…,n-1），考察这n个矩阵的连乘积$A_1{A}_2...A_n$ 。求出矩阵连乘积的最优计算次序。

问题分析：

由于矩阵乘法满足结合律，因此计算矩阵的连乘积可以有不同的计算次序，这种计算次序可以用加括号的方式来确定。例如A矩阵连乘积$A_1{A}_2{A}_3{A}_4$有5种完全加括号方式：$(A_1(A_2(A_3{A}_4)))$、$(A_1((A_2{A}_3)A_4))$、 ( ( A 1 A 2 ) ( A 3 A 4 ) ) ((A_1 A_2) (A_3 A_4)) ((A1​A2​)(A3</