布隆过滤器优化算法double—hashing论文原文（三）

引言

本论文来自leveldb源码中bloom.cc下布隆过滤器实现的代码注释中推荐的论文。论证了一种布隆过滤器的优化方式，带有详细的证明。是不可多得的好文章。其中的许多公式会对布隆过滤器相关的文章有所帮助。所以博主将原文和其中的海量公式转化为了可编辑的markdown和Latex，方便大家引用。如有转载，望注明论文出处和本文出处，谢谢！

论文原文出处：论文原文

本文作者：csdn账号，个人空间 - AcWing

受平台字数限制，只好将论文分成多段，望理解

上接 布隆过滤器优化算法double—hashing论文原文（二）

7. Multiple Queries

In the previous sections, we analyzed the behavior of $\mathbf{Pr}(\mathcal{F}(z))$ for some fixed Z and moderately sized TI .Unfortunately, this quantity is not directly of interest in most applications. Instead, one is usually concerned with certain characteristics of the distribution of the number of, say, $z_1,\dots ,z_{\ell }\in U-S$ for which $\mathcal{F}(z)$ occurs. In other words, rather than being interested in the probability that a particular false positive occurs, we are concerned with, for example, the fraction of distinct queries on elements of $U-S$ posed to the filter for which it returns false positives. Since { F ( z ) : z ∈ U − S } \{\mathcal{F}(z):z\in U-S\} {F(z):z∈U−S} are not independent, the behavior of $\mathbf{Pr}(\mathcal{F})$ alone does not directly imply results of this form. This section is devoted to overcoming this difficulty Now, it is easy to see that in the schemes that we analyze here, once the hash locations for every

$x\in S$ have been determined,the events { F ( z ) : z ∈ U − S } \{\mathcal{F}(z):z\in U-S\} {F(z):z∈U−S} are independent and occur with equal probability. More formally, letting $1(\cdot )$ denote the indicator function, { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} are conditionally independent and identically distributed given { H ( x ) : x ∈ S } \{H(x):x\in S\} {H(x):x∈S} . Thus, conditioned on { H ( x ) : x ∈ S } \{H(x):x\in S\} {H(x):x∈S} , an enormous number of classical convergence results (e.g. the law of large numbers and the central limit theorem) can be applied to { 1 ( F ( z ) ) : z ∈ U − S } \{1(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} These observations motivate a general technique for deriving the sort of convergence results

for { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} that one might desire in practice. First, we show that with high probability over the set of hash locations used by elements of S (that is, { H ( x ) :   x ∈ S } \{H(x):\:x\in S\} {H(x):x∈S} )，the random variables { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} are essentially independent Bernoulli trials with success probability ${\lim }_{n\to \infty }$Pr$(\mathcal{F})$ . From a technical standpoint, this result is the most important in this section. Next,we show how to use that result to prove counterparts to the classical convergence theorems mentioned above that hold in our setting Proceeding formally, we begin with a critical definition.

Definition 7.1. Consider any scheme where { H ( u ) : u ∈ U } \{H(u):u\in U\} {H(u):u∈U} are independent and identically distributed. Write S = { x 1 , … , x n } S=\{x_{1},\ldots,x_{n}\} S={x1​,…,xn​} .The false positive rate is defined to be the random variable
$$R=\mathbf{Pr}(\mathcal{F}\mid H(x_1),\dots ,H(x_n)).$$

---

The false positive rate gets its name from the fact that, conditioned on $R$ , the random variables { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} are independent Bernoulli trials with common success probability. $R$ .Thus, the fraction of a large number of queries on elements of $U-S$ posed to the filter for which it returns false positives is very likely to be close to $R$ .In this sense, $R$ ,while a random variable, acts like a rate for { 1 ( F ( z ) ) \{ \mathbf{1} ( \mathcal{F} ( z) ) {1(F(z)) : $z\in U-S\}$ It is important to note that in much of literature concerning standard Bloom filters,the false

positive rate is not defined as above.Instead the term is often used as a synonym for the false positive probability.Indeed, for a standard Bloom filter, the distinction between the two concepts as we have defined them is unimportant in practice, since, as mentioned in Section 2, one can easily show that $R.$ is very close to $\mathrm{Pr}(\mathcal{F})$ with extremely high probability (see, for example, [11]). It turns out that this result generalizes very naturally to the framework presented in this paper, and so the practical difference between the two concepts is largely unimportant even in our very general setting.However,the proof is more complicated than in the case of a standard Bloom filter, and so we will be very careful to use the terms as we have defined them.

Theorem 7.1.Consider a scheme where the conditions of Lemma 4.1 hold.Furthermore,assume that there is some function $y$ and independent identically distributed random variables. { V u : u ∈ U } \{V_{u}:u\in U\} {Vu​:u∈U} ，such that $V_u$ is uniform over $\mathrm{Supp}(V_u)$ ,，and for $u\in U$ ，we have $H(u)=g(V_u)$ Define

$$\begin{array}{rl}& p\stackrel{def}{=}{\left(1-{\mathrm{e}}^{-\lambda /k}\right)}^k\\ & \Delta \stackrel{def}{=}\underset{i\in H}{\max }\mathbf{Pr}(i\in H(u))-\frac{\lambda }{nk}(=o(1/n))\\ & \xi \stackrel{def}{=}nk\Delta (2\lambda +k\Delta )(=o(1))\end{array}$$

Then for any $ϵ=ϵ(n)>0$ with $ϵ=\omega (|\mathbf{Pr}(\mathcal{F})-p|)$ ,for n sufficiently large so that $ϵ>|\mathrm{Pr}(\mathcal{F})-p|$

$$\mathbf{Pr}(|R-p|>ϵ)\le 2\exp \left[\frac{-2n(ϵ-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right].$$

Furthermore, for any function. $h(n)$ = $o(\min (1/|\mathbf{Pr}(\mathcal{F})$ $-p|,\sqrt{n}))$ ，we have that $(R-p)h(n)$ converges to 0 in probability as $Tl\to \mathbf{x}$

Remark. Since $\left|\mathbf{Pr}(\mathcal{F})-p\right|=o(1)$ by Lemma 4.1, we may take $h(n)=1$ in Theorem 7.1 to conclude that $R$ converges to $P$ in probability as $Tl\to \infty$

Remark.From the proofs of Theorems 5.1 and 5.2,it is easy to see that for both the partition and (extended) double hashing schemes, $\Delta =0$ SO $\xi =0$ forboth schemes as well

Remark. We have added a new condition on the distribution of $H(u)$ , but it trivially holds in all of the schemes that we discuss in this paper (since, for independent fully random hash func tions $h_1$ and $h_2$ , the random variables $\{(h_1(u),h_2(u)):$ $u\in U\}$ are independent and identically distributed, and $(h_1(u),h_2(u))$ is uniformly distributed over its support).

Proof. The proof is essentially a standard application of Azuma’s inequality to an appropriately defined Doob martingale. Specifically, we employ the technique discussed in [12, Section 12.5] For convenience, write S = { x 1 , … , x n } S=\{x_{1},\ldots,x_{n}\} S={x1​,…,xn​} .For $h_1,\dots ,h_n\in$Supp$(H(u))$ ,define

$$f(h_1,\dots ,h_n)\stackrel{\mathrm{def}}{=}\mathbf{Pr}(\mathcal{F}\mid H(x_1)=h_1,\dots ,H(x_n)=h_n),$$

and note that $R=f(H(x_1),\dots ,H(x_n))$ .Now consider some $C$ such that for any $h_1,\dots ,h_j$ ， $h_j^{\prime }$ $h_{j+1},\dots ,h_n\in$Supp$(H(u))$

$$|f(h_1,\dots ,h_n)-f(h_1,\dots ,h_{j-1},h_j^{\prime },h_{j+1},\dots ,h_n)|\le c.$$

Since the $H(x_i)$ 's are independent, we may apply the result of [12, Section 12.5] to obtain

$$\mathbf{Pr}(|R-\mathbf{E}[R]|\ge \delta )\le 2{\mathrm{e}}^{-2{\delta }^2/n{c}^2},$$

for any $\delta >0$

To find a small choice for $t$ wewrite

∣ f ( h 1 , … , h n ) − f ( h 1 , … , h j − 1 , h j ′ , h j + 1 , … , h n ) ∣ = ∣ Pr ⁡ ( F ∣ H ( x 1 ) = h 1 , … , H ( x n ) = h n ) − Pr ⁡ ( F ∣ H ( x 1 ) = h 1 , … , H ( x j − 1 ) = h j − 1 , H ( x j ) = h j ′ , H ( x j + 1 ) = h j + 1 , … H ( x n ) = ∣ ∣ { v ∈ S u p p ( V u ) : g ( v ) ⊆ ⋃ i = 1 n h i } ∣ − ∣ { v ∈ S u p p ( V u ) : g ( v ) ⊆ ⋃ i = 1 n { h j ′ i = j h i i ≠ j } ∣ ∣ S u p p ( V u ) ∣ ≤ max ⁡ v ′ ∈ S u p p ( V u ) ∣ { v ∈ S u p p ( V u ) : ∣ g ( v ) ∩ g ( v ′ ) ∣ ≥ 1 } ∣ ∣ S u p p ( V u ) ∣ = max ⁡ M ′ ∈ S u p p ( H ( u ) ) P r ( ∣ H ( u ) ∩ M ′ ∣ ≥ 1 ) , \left.\begin{aligned}&\left|f(h_{1},\ldots,h_{n})-f(h_{1},\ldots,h_{j-1},h_{j}^{\prime},h_{j+1},\ldots,h_{n})\right|\\&=\left|\Pr(\mathcal{F}\mid H(x_{1})=h_{1},\ldots,H(x_{n})=h_{n})\right.\\&-\Pr(\mathcal{F}\mid H(x_{1})=h_{1},\ldots,H(x_{j-1})=h_{j-1},H(x_{j})=h_{j}^{\prime},H(x_{j+1})=h_{j+1},\ldots H(x_{n})\\&=\frac{\left|\left|\{v\in\mathrm{Supp}(V_u):g(v)\subseteq\bigcup_{i=1}^nh_i\}\right|-\left|\left\{v\in\mathrm{Supp}(V_u):g(v)\subseteq\bigcup_{i=1}^n\left\{\begin{array}{c}h_j^{\prime}&i=j\\h_i&i\neq j\end{array}\right.\right.\right\}\right|}{\left|\mathrm{Supp}(V_u)\right|}\\&\leq\frac{\max_{v^{\prime}\in\mathrm{Supp}(V_u)}\mid\{v\in\mathrm{Supp}(V_u):|g(v)\cap g(v^{\prime})|\geq1\}\mid}{\left|\mathrm{Supp}(V_u)\right|}\\&=\max_{M^{\prime}\in\mathrm{Supp}(H(u))}\mathbf{Pr}(|H(u)\cap M^{\prime}|\geq1),\end{aligned}\right. ​ ​f(h1​,…,hn​)−f(h1​,…,hj−1​,hj′​,hj+1​,…,hn​) ​=∣Pr(F∣H(x1​)=h1​,…,H(xn​)=hn​)−Pr(F∣H(x1​)=h1​,…,H(xj−1​)=hj−1​,H(xj​)=hj′​,H(xj+1​)=hj+1​,…H(xn​)=∣Supp(Vu​)∣ ​∣{v∈Supp(Vu​):g(v)⊆⋃i=1n​hi​}∣− ​{v∈Supp(Vu​):g(v)⊆⋃i=1n​{hj′​hi​​i=ji=j​} ​​≤∣Supp(Vu​)∣maxv′∈Supp(Vu​)​∣{v∈Supp(Vu​):∣g(v)∩g(v′)∣≥1}∣​=M′∈Supp(H(u))max​Pr(∣H(u)∩M′∣≥1),​

where the first step is just the definition of $f$ ，the second step follows from the definitions of $V_u$ and $y$ ,the third step holds since changing one of the $h_i$ 's to some $M^{\prime }\in \mathrm{Supp}(H(u))$ cannot change

$$\left|\left\{v\in \mathrm{Supp}(V_u):g(v)\subseteq \bigcup _{i=1}^n{h}_i\right\}\right|$$

bv more than

∣ { v ∈ S u p p ( V u )   :   ∣ g ( v ) ∩ M ′ ∣ ≥ 1 } ∣ , \left|\left\{v\in\mathrm{Supp}(V_u)\::\:|g(v)\cap M'|\geq1\right\}\right|, ∣{v∈Supp(Vu​):∣g(v)∩M′∣≥1}∣,

and the fourth step follows from the definitions of $V_u$ and $y$

Now consider any fixed $M^{\prime }\in \mathrm{Supp}(H(u))$ , and let $y_1,\dots ,y_{|M^{\prime }|}$ be the distinct elements of $M^{\prime }$ .Recall that $\Vert M^{\prime }\Vert =k$ ,SO $|M^{\prime }|\le k$ .Applying a union bound,we have that

$$\begin{array}{rl}\mathbf{Pr}(|H(u)\cap M^{\prime }|\ge 1)& =\mathbf{Pr}\left(\bigcup _{i=1}^{|M^{\prime }|}{y}_i\in H(u)\right)\\ & \le \sum _{i=1}^{|M^{\prime }|}\mathbf{Pr}(y_i\in H(u))\\ & \le \sum _{i=1}^{|M^{\prime }|}\frac{\lambda }{kn}+\Delta \\ & \le \frac{\lambda }{n}+k\Delta .\end{array}$$

Therefore, we may set $c=\frac{\lambda }{n}+k\Delta$ to obtain

$$\mathbf{Pr}(|R-\mathbf{E}[R]|>\delta )\le 2\exp \left[\frac{-2n{\delta }^2}{{\lambda }^2+\xi }\right],$$

for any $\delta >0$ .Since $\mathbf{E}[R]=$Pr$(\mathcal{F})$ , we write (for sufficiently large $Tl.$ so that $ϵ>|\mathbf{Pr}(\mathcal{F})-p|)$

$$\begin{array}{rl}\mathbf{Pr}(|R-p|>ϵ)& \le \mathbf{Pr}(|R-\mathbf{Pr}(\mathcal{F})|>ϵ-|\mathbf{Pr}(\mathcal{F})-p|)\\ & \le 2\exp \left[\frac{-2n(ϵ-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right].\end{array}$$

To complete the proof, we see that for any constant $\delta >0$

$$\mathbf{Pr}(|R-p|h(n)>\delta )=\mathbf{Pr}(|R-p|>\delta /h(n))\to 0\mathrm{as}n\to \infty ,$$

where the second step follows from the fact that $|\mathbf{Pr}(\mathcal{F})-p|=o(1/h(n))$ so for sufficiently large 77. ，

$$\begin{array}{rl}\mathbf{Pr}(|R-p|>\delta /h(n))& \le 2\exp \left[\frac{-2n(\delta /h(n)-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right]\\ & \le 2\exp \left[-\frac{{\delta }^2}{{\lambda }^2+\xi }\cdot \frac{n}{h(n{)}^2}\right]\\ & \to 0\mathrm{as}n\to \infty ,\end{array}$$

and the last step follows from the fact that $h(n)=o(\sqrt{n})$

Since, conditioned on $R.$ ,the events { F ( z ) : z ∈ U − S } \{{\mathcal{F}}(z):z\in U-S\} {F(z):z∈U−S} are independent and each occur witl probability $R.$ ，Theorem 7.1 suggests that { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} are essentially independent Bernoulli trials with success probability $/\mu$ .The next result is a formalization of this idea.

Lemma 7.1.Consider a scheme where the conditions of Theorem 7.1 hold.Let ${\mathcal{F}}_{n_0}(z)$ denote $\mathcal{F}(z)$ in the case when the schemeis used with ${\eta }_l={\eta }_0$ .Similarly, let $R_{n_0}$ denote $R$ in the case where $\mathbf{T}\mathbf{l}={\mathbf{Y}\mathbf{l}}_0$ .Let { X n } \{X_{n}\} {Xn​} be a sequence of real-valued random variables, where each. $X_n$ can be erpressed as some function of { 1 ( F n ( z ) ) : \{ \mathbf{1} ( \mathcal{F} _{n}( z) ) : {1(Fn​(z)): $z\in U-S\}$ ,and let $Y$ be any probability distribution on $1\mathbb{R}$ .Then for every $x\in \mathbb{R}$ and $ϵ=ϵ(n)>0$ with $ϵ=\omega (|\mathbf{Pr}(\mathcal{F})-p|)$ ，for sufficiently large $TI$ so that $ϵ>\left|\mathrm{Pr}(\mathcal{F})-p\right|$

$$\begin{array}{rl}|\mathrm{Pr}(X_n\le x)-\mathrm{Pr}(Y\le x)|\le |\mathrm{Pr}(X_n\le x\mid |R_n-p|\le ϵ)-\mathrm{Pr}(Y\le x)|& \\ & +2\exp \left[\frac{-2n(ϵ-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right].\end{array}$$

Proof. The proof is a straightforward application of Theorem 7.1.Fix any $x\in$ 18 ,and choose some $E$ satisfying the conditions of the lemma. Ther.

$$\begin{array}{rl}{}_n\le x)& =\mathbf{Pr}(X_n\le x,|R_n-p|>ϵ)+\mathbf{Pr}(X_n\le x,|R_n-p|\le ϵ)\\ & =\mathbf{Pr}(X_n\le x\mid |R_n-p|\le ϵ)\\ & +\mathbf{Pr}(|R_n-p|>ϵ)\left[\mathbf{Pr}(X_n\le x\mid |R_n-p|>ϵ)-\mathbf{Pr}(X_n\le x\mid |R_n-p|\le ϵ\right]\end{array}$$

implying that

$$|\mathrm{Pr}(X_n\le x)-\mathrm{Pr}(X_n\le x\mid |R_n-p|\le ϵ)|\le \mathrm{Pr}(|R_n-p|>ϵ).$$

Therefore,

$$\begin{array}{rl}& (X_n\le x)-\mathbf{Pr}(Y\le x)|\\ & \mathbf{Pr}(X_n\le x)-\mathbf{Pr}(X_n\le x\mid |R_n-p|\le ϵ)|+|\mathbf{Pr}(X_n\le x\mid |R_n-p|\le ϵ)-\mathbf{Pr}(Y_n\le x)\\ & \mathbf{Pr}(|R_n-p|>ϵ)+|\mathbf{Pr}(X_n\le x\mid |R_n-p|\le ϵ)-\mathbf{Pr}(Y_n\le x)|,\end{array}$$

so for sufficiently large $Tl.$ so that $ϵ>\left|\mathbf{Pr}(\mathcal{F})-p\right|$

$$\begin{array}{rl}|\mathrm{Pr}(X_n\le x)-\mathrm{Pr}(Y\le x)|\le |\mathrm{Pr}(X_n\le x\mid |R_n-p|\le ϵ)-\mathrm{Pr}(Y\le x)|& \\ & +2\exp \left[\frac{-2n(ϵ-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right],\end{array}$$

by Theorem 7.1.

Toillustrate the power of Theorem7.1andLemma 7.1,we use them to prove versions of the strong law oflarge numbers.the weak law of large numbers.Hoeffding’s inequality,and the central limit theorem.

Theorem 7.2.Consider a scheme that satisfies the conditions of Theorem 7.1.Let $Z\subseteq U-S$ be countably infinite,and write Z = { z 1 , z 2 , … } Z=\{z_{1},z_{2},\ldots\} Z={z1​,z2​,…} .Then for any $ϵ>0$ ，for n sufficiently large so that $ϵ>\left|\mathbf{Pr}(\mathcal{F})-p\right|$ ,we have.

$$\mathrm{Pr}\left(\underset{\ell \to \infty }{\lim }\frac{1}{\ell }\sum _{i=1}^{\ell }1({\mathcal{F}}_n(z_i))=R_n\right)=1.$$

2.For any $ϵ>0$ ,for TI sufficiently large so that $ϵ>\left|\mathrm{Pr}(\mathcal{F})-p\right|$

$$\mathbf{Pr}\left(\left|\underset{\ell \to \infty }{\lim }\frac{1}{\ell }\sum _{i=1}^{\ell }1({\mathcal{F}}_n(z_i))-p\right|>ϵ\right)\le 2\exp \left[\frac{-2n(ϵ-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right].$$

In particular, ${\lim }_{\ell \to \infty }\frac{1}{\ell }{\sum }_{i=1}^{\ell }1({\mathcal{F}}_n(z_i))$ converges to $P$ in probability as $7l\to 0$

3.For any function $Q(n)$ ， $ϵ>0$ ,andn sufficiently large so that $ϵ/2>\left|\mathbf{Pr}(\mathcal{F})-p\right|$

Pr
$$\mathbf{r}\left(\left|\frac{1}{Q(n)}\sum _{i=1}^{Q(n)}1({\mathcal{F}}_n(z_i))-p\right|>ϵ\right)\le 2{\mathrm{e}}^{-Q(n){ϵ}^2/2}+2\exp \left[\frac{-2n(ϵ/2-|\mathbf{Pr}(\mathcal{F})-p|{)}^2}{{\lambda }^2+\xi }\right].$$

4.For any function $Q(n)$ with ${\lim }_{n\to \infty }Q(n)=\infty$ and $Q(n)=o(\min (1/|\mathbf{Pr}(\mathcal{F})-p{|}^2,n))$

${\sum }_{i=1}^{Q(n)}\frac{1({\mathcal{F}}_n(z_i))-p}{\sqrt{Q(n)p(1-p)}}\to$N(0,1) in itituin s $7l\to 0$

Remark. By Theorems 6.2 and 6.3, $|\mathbf{Pr}(\mathcal{F})-p|=\Theta (1/n)$ for both the partition and double hashing schemes introduced in Section 5. Thus, for each of the schemes, the condition $Q(n)=$ $o(\min (1/|\mathbf{Pr}(\mathcal{F})-p{|}^2,n))$ in the fourth part of Theorem 7.2 becomes $Q(n)=o(n)$

Proof. Since, given $R_n$ , the random variables { 1 ( F n ( z ) ) : z ∈ Z } \{\mathbf{1}(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn​(z)):z∈Z} are conditionally independent Bernoulli trials with common success probability $R_n$ ，a direct application of the strong law of large numbers yields the first item. For the second item.we note that the first item implies that

$$\underset{\ell \to \infty }{\lim }\frac{1}{\ell }\sum _{i=1}^{\ell }1({\mathcal{F}}_n(z_i))\sim R_n.$$

A direct application of Theorem 7.1 then gives the result.

The remaining two items are slightly more difficult.However, they can be dealt with using straightforward applications of Lemma 7.1. For the third item,define

$$X_n\stackrel{\mathrm{def}}{=}\left|\frac{1}{Q(n)}\sum _{i=1}^{Q(n)}1({\mathcal{F}}_n(z_i))-p\right|.$$

and $Y\stackrel{\det }{=}0$ .Let =e/2to obtain

$$\begin{array}{rl}& \mathbf{Pr}(X_n>ϵ\mid |R_n-p|\le \delta )\\ & =\mathbf{Pr}\left(\left|\sum _{i=1}^{Q(n)}1({\mathcal{F}}_n(z_i))-Q(n)p\right|>Q(n)ϵ||R_n-p|\le \delta \right)\\ & \le \mathbf{Pr}\left(\left|\sum _{i=1}^{Q(n)}1({\mathcal{F}}_n(z_i))-Q(n)R_n\right|>Q(n)\left(ϵ-|R_n-p|\right)||R_n-p|\le \delta \right)\\ & \le \mathbf{Pr}\left(\left|\sum _{i=1}^{Q(n)}1({\mathcal{F}}_n(z_i))-Q(n)R_n\right|>\frac{Q(n)ϵ}{2}||R_n-p|\le \delta \right)\\ & \le 2{\mathrm{e}}^{-Q(n)t^2/2},\end{array}$$

where the first two steps are obvious, the third step follows from the fact that $\mathbf{Pr}({\mathcal{F}}_n\mid R_n)=R_n$ and the fourth step is an application of Hoeffding’s Inequality (using the fact that, given $R_n$ { 1 ( F n ( z ) ) : z ∈ Z } \{1(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn​(z)):z∈Z} are independent and identically distributed Bernoulli trials with commor success probability $R_n$ ).

Now, since $\mathbf{Pr}(Y\le ϵ)=1$

$$\mathbf{Pr}(X_n\le ϵ\mid |R_n-p|\le \delta )-\mathbf{Pr}(Y\le ϵ)|=\mathbf{Pr}(X_n>ϵ\mid |R_n-p|\le \delta )\le 2{\mathrm{e}}^{-Q(n){ϵ}^2/2}.$$

An application of Lemma 7.1 now gives the third item. For the fourth item, we write

Q(n) >
$$\frac{1({\mathcal{F}}_n(z_i))-p}{\sqrt{Q(n)p(1-p)}}=\sqrt{\frac{R_n(1-R_n)}{p(1-p)}}\left(\sum _{i=1}^{Q(n)}\frac{1({\mathcal{F}}_n(z_i))-R_n}{\sqrt{Q(n)R_n(1-R_n)}}+(R_n-p)\sqrt{\frac{Q(n)}{R_n(1-R_n)}}\right)$$

By the central limit theorem,

$$\sum _{i=1}^{Q(n)}\frac{1({\mathcal{F}}_n(z_i))-R_n}{\sqrt{Q(n)R_n(1-R_n)}}\to \mathrm{N}(0,1)\text{in distribution as}n\to \infty ,$$

since, given $R_n$ ， { 1 ( F n ( z ) ) : z ∈ Z } \{\mathbf{1}(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn​(z)):z∈Z} are independent and identically distributed Bernoulli trials with common success probability $R_n$ . Furthermore, $R_n$ converges to $F$ in probability as $Tl\to \mathbf{x}$ by Theorem 7.1,so it suffices to show that $(R_n-p)\sqrt{Q(n)}$ converges to 0 in probability as ${\eta }_b\to \mathbf{x}$ .But $\sqrt{Q(n)}=o(\min (1/|\mathbf{Pr}(\mathcal{F})-p|,\sqrt{n}))$ , so another application of Theorem 7.1 gives the result. L

8. Experiments

In this section,we evaluate the theoretical results of the previous sections empirically for small values of $7l$ .We are interested in the following specific schemes: the standard Bloom filter scheme, the partition scheme, the double hashing scheme, and the extended double hashing schemes where $f(i)=i^2$ and $f(i)=i^3$ For c ∈ { 4 , 8 , 12 , 16 } c\in\{4,8,12,16\} c∈{4,8,12,16} ,we do the following. First, compute the value of $k\in \{\lfloor c\ln 2\rfloor ,\lceil c\ln 2\rceil \}$

that minimizes $p=(1-\exp [-k/c]{)}^k$ .Next, for each of the schemes under consideration, repeat the following procedure 10,000 times:instantiate the filter with the specified values of $7l$ ， $C$

---

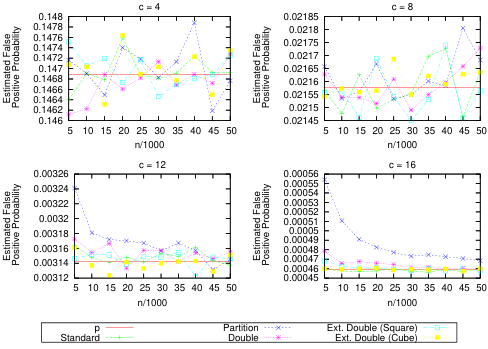
Figure 1: Estimates of the false positive probability for various schemes and parameters.

and $k$ ,populate the filter with a set $S$ of $7L$ items, and then query $\lceil 10/p\rceil$ elements not in $S$ recording the number $Q$ of those queries for which the filter returns a false positive.We then approximate the false positive probability of the scheme by averaging the results over all 10,000 trials. Furthermore, we bin the results of the trials by their values for $CQ$ in order to examine the other characteristics of $Q$ 's distribution.

The results are shown in Figures 1 and 2. In Figure 1, we see that for small values of $C$ the different schemes are essentially indistinguishable from each other, and simultaneously have a false positive probability/rate close to $P$ .This result is particularly significant since the filters that we are experimenting with are fairly small, supporting our claim that these schemes are useful even in settings with very limited space. However, we also see that for the slightly larger values of c ∈ { 12 , 16 } c\in\{12,16\} c∈{12,16} , the partition scheme is no longer particularly useful for small values of $7L$ ,while the other schemes are.This result is not particularly surprising, since we know from Section 6 that all of these schemes are unsuitable for small values of $Tl.$ and large values of $\mathbf{C}$ . Furthermore, we expect that the partition scheme is the least suited to these conditions, given the observation in Section 2 that the partitioned version of a standard Bloom filter never performs better than the original version. Nevertheless, the partition scheme might still be useful in certain settings, since it gives a substantial reduction in the range of the hash functions. In Figure 2, we give histograms of the results from our experiments with $n=5000$ and $c=8$

for the partition and extended double hashing schemes. Note that for this value of $C$ , optimizing for $k$ yields $k=6$ ,so we have $p\approx 0.021577$ and $\lceil 10/p\rceil =464$ .In each plot, we compare the results to $f\stackrel{\mathrm{def}}{=}10,000{\varphi }_{464p,464p(1-p)}$ ,where

$${\varphi }_{\mu ,{\sigma }^2}(x)\stackrel{\mathrm{def}}{=}\frac{{\mathrm{e}}^{-(x-\mu {)}^2/2{\sigma }^2}}{\sigma \sqrt{2\pi }}$$

denotes the density function of $\mathrm{N}(\mu ,{\sigma }^2)$ .As one would expect, given central limit theorem in the fourth part of Theorem 7.2, $f$ provides a reasonable approximation to each of the histograms

---

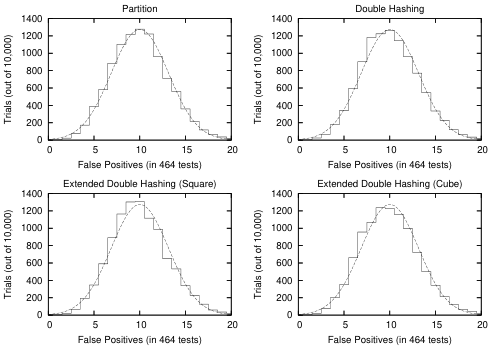
Figure 2: Estimate of distribution of $CQ$ (for $n=5000$ and $c=8$ ),compared with $f$

9. A Modified Count-Min Sketch

We now present a modification to the Count-Min sketch introduced in [4] that uses fewer hash functions in a manner similar to our improvement for Bloom filters, at the cost of a small space increase.We begin by reviewing the original data structure.

9.1 Count-Min Sketch Review

The following is an abbreviated review of the description given in [4].A Count-Min sketch takes as input a stream of updates $(i_t,c_t)$ ，starting from $t=1$ ，where each item $i_t$ is a member of a universe U = { 1 , … , n } U=\{1,\ldots,n\} U={1,…,n} ,and each count $Ct$ is a positive number.(Extensions to negative counts are possible;we do not consider them here for convenience.)The state of the system at time $T$ is given by a vector $\vec{a}(T)=(a_1(T),\dots ,a_n(T))$ ,where $a_j(T)$ is the sum of all $Ct$ for which $t\le T$ and $i_t=j$ .We generally drop the $I$ when the meaning is clear. The Count-Min sketch consists of an array Count of width $w\stackrel{\mathrm{def}}{=}\lceil \mathrm{e}/ϵ\rceil$ and depth $d\stackrel{\mathrm{def}}{=}\lceil \ln 1/\delta \rceil$

Count$[1,1],\dots$,Count$[d,w]$ .Every entry of the array is initialized to $U$ .In addition,the CountMin sketch uses $d$ hash functions chosen independently from a pairwise independent family $H$ ： { 1 , … , n } → { 1 , … , w } \{1,\ldots,n\}\to\{1,\ldots,w\} {1,…,n}→{1,…,w} The mechanics of the Count-Min sketch are extremely simple.Whenever an update $(i,c)$

arrives, we increment $\mathrm{Count}[j,h_j(i)]$ by $t$ for $j=1,\dots ,d$ .Whenever we want an estimate of $u_i$ (called a point query),we compute
$${\hat{a}}_i\stackrel{\mathrm{def}}{=}\underset{j=1}{\overset{d}{\min }}\mathrm{Count}[j,h_j(i)].$$
The fundamentalresult of Count-Min sketches is that for every $\dot{\tau }$
$${\hat{a}}_i\ge a\mathrm{and}\mathbf{Pr}({\hat{a}}_i\le a_i+ϵ\Vert \vec{a}\Vert )\ge 1-\delta ,$$

---

where the norm is the $L_1$ norm. Surprisingly,this very simple bound allows for a number of sophisticated estimation procedures to be efficiently and effectively implemented on Count-Min sketches. The reader is once again referred to [4] for details.

9.2Using Fewer Hash Functions

We now show how the improvements to Bloom filters discussed previously in this paper can be usefully applied to Count-Min sketches. Our modification maintains all of the essential features of Count-Min sketches, but reduces the required number of pairwise independent hash functions to $2\lceil (\ln 1/\delta )/(\ln 1/ϵ)\rceil$ .We expect that, in many settings, $E$ and $\delta$ will be related, so that only a constant number of hash functions will be required; in fact, in many such situations only two hash functions are required. We describe a variation of the Count-Min sketch that uses just two pairwise independent hash

functions and guarantees that

$${\hat{a}}_i\ge a\mathrm{and}\mathbf{Pr}({\hat{a}}_i\le a_i+ϵ\Vert \vec{a}\Vert )\ge 1-ϵ.$$

Given such a result, it is straightforward to obtain a variation that uses $2\lceil (\ln 1/\delta )/(\ln 1/ϵ)\rceil$ pairwise independent hash functions and achieves the desired failure probability $\delta$ : simply build $2\lceil (\ln 1/\delta )/(\ln 1/ϵ)\rceil$ independent copies of this data structure, and always answer a point query with the minimum estimate given by one of those copies. Our variation will use $d$ tables numbered { 0 , 1 , … , d − 1 } \{0,1,\ldots,d-1\} {0,1,…,d−1} ，each with exactly $ub$ counters

numbered { 0 , 1 , … , w − 1 } \{0,1,\ldots,w-1\} {0,1,…,w−1} ，where $d$ and $UD$ will be specified later.We insist that $ub$ be prime. Just as in the original Count-Min sketch, we let $\mathrm{Count}[j,k]$ denote the value of the $k$ th counter in the $j$ th table. We choose hash functions $h_1$ and $h_2$ independently from a pairwise independent. family H : { 0 , … , n − 1 } {\mathcal{H} }: \{ 0, \ldots , n- 1\} H:{0,…,n−1} $\to$ { 0 , 1 , … , w − 1 } \{ 0, 1, \ldots , w- 1\} {0,1,…,w−1} ，and define $g_j(x)$ = $h_1(x)$ + $j{h}_2(x)$ mod $U$ for $j=0,\dots ,d-1$ The mechanics of our data structure are the same as for the original Count-Min sketch.

Whenever an update $(i,c)$ occurs in the stream, we increment $\mathrm{Count}[j,g_j(i)]$ by $t$ ，for $j=$ $0,\dots ,d-1$ .Whenever we want an estimate of $u_i$ ，we compute

$${\hat{a}}_i\stackrel{\mathrm{def}}{=}\underset{j=0}{\overset{d-1}{\min }}\mathrm{Count}[j,g_j(i)].$$

We prove the following result:

Theorem 9.1. For the Count-Min sketch variation described above.

$${\hat{a}}_i\ge aand\mathbf{Pr}({\hat{a}}_i>a_i+ϵ\Vert \vec{a}\Vert )\le \frac{2}{ϵw^2}+{\left(\frac{2}{ϵw}\right)}^d.$$

In particular, for $w\ge 2$e$/ϵ$ and $\delta \ge \ln 1/ϵ(1-1/2{\mathrm{e}}^2)$

$${\hat{a}}_i\ge aand\mathbf{Pr}({\hat{a}}_i>a_i+ϵ\Vert \vec{a}\Vert )\le ϵ.$$

Proof. Fix some item $i$ .Let $A_i$ be the total count for all items Z (besides $\dot{i}$ ）with $h_1(z)=h_1(i)$ and $h_2(z)=h_2(i)$ .Let $B_{j,i}$ be the total count for all items Z with $g_j(i)=g_j(z)$ ,excluding $i$ and items 2 counted in $A_i$ .It follows that

$${\hat{a}}_i=\underset{j=0}{\overset{d-1}{\min }}\text{Count}[j,g_j(i)]=a_i+A_i+\underset{j=0}{\overset{d-1}{\min }}{B}_{j,i}.$$

---

Thelower bound now follows immediately from the fact thatallitems have nonnegative counts. since all updates are positive. Thus, we concentrate on the upper bound, which we approach by noticing that
$$\mathbf{Pr}({\hat{a}}_i\ge a_i+ϵ\Vert \vec{a}\Vert )\le \mathbf{Pr}(A_i\ge ϵ\Vert \vec{a}\Vert /2)+\mathbf{Pr}\left(\underset{j=0}{\overset{d-1}{\min }}{B}_{j,i}\ge ϵ\Vert \vec{a}\Vert /2\right).$$
We first bound $A_i$ . Letting $1(\cdot )$ denote the indicator function,we have
$$\mathbf{E}[A_i]=\sum _{z\ne i}{a}_z\mathbf{E}[1(h_1(z)=h_1(i)\wedge h_2(z)=h_2(i))]\le \sum _{z\ne i}{a}_z/w^2\le \Vert \vec{a}\Vert /w^2,$$
where the first step follows from linearity of expectation and the second step follows from the definition of the hash functions.Markov’s inequality now implies that
$$\mathrm{Pr}(A_i\ge ϵ\Vert \vec{a}\Vert /2)\le 2/ϵw^2.$$
To bound ${\min }_{j=0}^{d-1}{B}_{j,i}$ ,we note that for any j ∈ { 0 , … , d − 1 } j\in\{0,\ldots,d-1\} j∈{0,…,d−1} and $z\ne i$
$$\begin{array}{rl}\mathbf{Pr}((h_1(z)\ne h_1(i)\vee h_2(z)\ne h_2(i))\wedge g_j(z)=g_j(i))& \le \mathbf{Pr}(g_j(z)=g_j(i))\\ & =\mathbf{Pr}(h_1(z)=h_1(i)+j(h_2(i)-h_2(z))\\ & =1/w,\end{array}$$
SO
$$\mathbf{E}[B_{j,i}]=\sum _{z\ne i}{a}_z\mathbf{E}[1((h_1(z)\ne h_1(i)\vee h_2(z)\ne h_2(i))\wedge g_j(z)=g_j(i))]\le \Vert \vec{a}\Vert /w,$$
and so Markov’s inequality implies that
$$\mathbf{Pr}(B_{j,i}\ge ϵ\Vert \vec{a}\Vert /2)\le 2/ϵw$$
For arbitrary $ub$ , this result is not strong enough to bound ${\min }_{j=0}^{d-1}{B}_{j,i}.$ However, since $ub$ is prime, each item $Z$ can only contribute to one $B_{k,i}$ (since if $g_j(z)=g_j(i)$ for two values of $j$ ,we must have $h_1(z)=h_1(i)$ and $h_2(z)=h_2(i)$ , and in this case 2 's count is not included in any $B_{j,i}$ ). In this sense, the $B_{j,i}$ 's are negatively dependent [7]. It follows that for any value $U$
$$\mathbf{Pr}\left(\underset{j=0}{\overset{d-1}{\min }}{B}_{j,i}\ge v\right)\le \prod _{j=0}^{d-1}\mathbf{Pr}(B_{j,i}\ge v).$$
In particular,we have that
$$\mathbf{Pr}\left(\underset{j=0}{\overset{d-1}{\min }}{B}_{j,i}\ge ϵ\Vert \vec{a}\Vert /2\right)\le (2/ϵw{)}^d,$$
SO
$$\begin{array}{rl}\mathbf{Pr}({\hat{a}}_i\ge a_i+ϵ\Vert \vec{a}\Vert )& \le \mathbf{Pr}(A_i\ge ϵ\Vert \vec{a}\Vert /2)+\mathbf{Pr}\left(\underset{j=0}{\min }{B}_j,i\ge ϵ\Vert \vec{a}\Vert /2\right)\\ & \le \frac{2}{ϵw^2}+{\left(\frac{2}{ϵw}\right)}^d.\end{array}$$
And for $w\ge 2$e$/ϵ$ and $\delta \ge \ln 1/ϵ(1-1/2{\mathrm{e}}^2)$ ,we have
$$\begin{array}{r}\frac{2}{ϵw^2}+{\left(\frac{2}{ϵw}\right)}^d\le ϵ/2e^2+ϵ(1-1/2{\text{e}}^2)=ϵ,\end{array}$$
completing the proof

---

10. Conclusion

Bloom filters are simple randomized data structures that are extremely useful in practice.In fact, they are so useful that any significant reduction in the time required to perform a Bloom filter operation immediately translates to a substantial speedup for many practical applications Unfortunately, Bloom filters are so simple that they do not leave much room for optimization. This paper focuses on modifying Bloom filters to use less of the only resource that they tradi-

tionally use liberally: (pseudo)randomness. Since the only nontrivial computations performed by. a Bloom filter are the constructions and evaluations of pseudorandom hash functions, any reduction in the required number of pseudorandom hash functions yields a nearly equivalent reduction in the time required to perform a Bloom filter operation (assuming, of course, that the Bloom filter is stored entirely in memory, so that random accesses can be performed very quickly) We have shown that a Bloom filter can be implemented with only two pseudorandom hash

functions without any increase in the asymptotic false positive probability, and, for Bloom filters of fixed size with reasonable parameters,without any substantial increase in the false positive probability.We have also shown that the asymptotic false positive probability acts,for all practical purposes and reasonable settings of a Bloom filter’s parameters, like a false positive rate. This result has enormous practical significance, since the analogous result for standard Bloom filters is essentially the theoretical justification for their extensive use… More generally, we have given a general framework for analyzing modified Bloom filters, which

we expect will be used in the future to refine the specific schemes that we analyzed in this paper. We also expect that the techniques used in this paper will be usefully applied to other data structures, as demonstrated by our modification to the Count-Min sketch.

Acknowledgements

We are very grateful to Peter Dillinger and Panagiotis Manolios for introducing us to this problem, providing us with advance copies of their work, and also for many useful discussions.

References

[1] P. Billingsley. Probability and Measure, Third Edition. John Wiley & Sons, 1995.

[2] P. Bose, H. Guo, E. Kranakis, A. Maheshwari, P. Morin, J. Morrison, M. Smid, and Y Tang. On the false-positive rate of Bloom filters. Submitted. Temporary version available at http://cg.scs.carleton.ca/~morin/publications/ds/bloom-submitted.pdf [3]A. Broder and M. Mitzenmacher. Network Applications of Bloom Filters: A Survey. Internet Mathematics, to appear. Temporary version available at http: //www.eecs.harvard. edu/. ~michaelm/postscripts/tempim3.pdf [4] G. Cormode and S. Muthukrishnan. Improved Data Stream Summaries: The Count-Min Sketch and its Applications. DIMACS Technical Report 2003-20, 2003 [5]P. C. Dillinger and P. Manolios. Bloom Filters in Probabilistic Verification. FMCAD 2004, Formal Methods in Computer-Aided Design, 2004. [6]P. C. Dillinger and P. Manolios. Fast and Accurate Bitstate Verification for SPIN. SPIN 2004, 11th International SPIN Workshop on Model Checking of Software, 2004.

---

[7]D. P. Dubhashi and D. Ranjan. Balls and Bins: A Case Study in Negative Dependence. Random Structures and Algorithms, 13(2):99-124, 1998 [8]L.Fan, P. Cao, J. Almeida,and A. Z. Broder. Summary cache: a scalable wide-area Web cache sharing protocol. IEEE/ACM Transactions on Networking, 8(3):281-293, 2000 [9] K. Ireland and M. Rosen. A Classical Introduction to Modern Number Theory, Second Edition. Springer-Verlag, New York, 1990 [10]D. Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching. AddisonWesley, Reading Massachusetts, 1973. [11] M. Mitzenmacher. Compressed Bloom Filters. IEEE/ACM Transactions on Networking. 105:613-620, 2002 [12] M. Mitzenmacher and E. Upfal. Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, 2005. [13] M. V. Ramakrishna. Practical performance of Bloom filters and parallel free-text searching Communications of the ACM, 32(10):1237-1239, 1989.