引言
本论文来自leveldb源码中bloom.cc下布隆过滤器实现的代码注释中推荐的论文。论证了一种布隆过滤器的优化方式,带有详细的证明。是不可多得的好文章。其中的许多公式会对布隆过滤器相关的文章有所帮助。**所以博主将论文和其中的海量公式转化为了可编辑的markdown和Latex,并在机翻的基础上,通读论文并对翻译的不足进行修改和润色。**方便大家引用。如有转载,望注明论文出处和本文出处,谢谢!
论文原文出处:论文原文
本文作者:csdn账号,个人空间 - AcWing
受平台字数限制,只好将论文分成多段,望理解
7. 多个查询
在前面的部分中,我们分析了 P r ( F ( z ) ) \mathbf{Pr}(\mathcal{F}(z)) Pr(F(z)) 对于一些固定 Z 和中等大小的 TI 的行为。遗憾的是,在大多数应用中,这个量并不直接相关。相反,人们通常关心 F ( z ) \mathcal{F}(z) F(z) 出现的 z 1 , … , z ℓ ∈ U − S z_{1},\ldots,z_{\ell}\in U-S z1,…,zℓ∈U−S 的数量分布的某些特征。换句话说,我们关心的不是特定误报发生的概率,而是关心,例如,对 U − S U-S U−S 元素的不同查询对过滤器的不同查询的比例,它返回假阳性。由于 { F ( z ) : z ∈ U − S } \{\mathcal{F}(z):z\in U-S\} {F(z):z∈U−S} 不是独立的,因此 P r ( F ) \mathbf{Pr}(\mathcal{F}) Pr(F) 的行为本身并不直接意味着这种形式的结果。本节致力于克服这个困难 现在,很容易看出,在我们在这里分析的 schemes 中,一旦每个
x ∈ S x\in S x∈S 已经确定,事件 { F ( z ) : z ∈ U − S } \{\mathcal{F}(z):z\in U-S\} {F(z):z∈U−S} 是独立的,并且以相等的概率发生。更正式地说,让 1 ( ⋅ ) 1(\cdot) 1(⋅) 表示指示函数, { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} 是条件独立的,并且在给定 { H ( x ) : x ∈ S } \{H(x):x\in S\} {H(x):x∈S} 的情况下分布相同。因此,以 { H ( x ) : x ∈ S } \{H(x):x\in S\} {H(x):x∈S} 为条件,大量的经典收敛结果(例如大数定律和中心极限定理)可以应用于 { 1 ( F ( z ) ) : z ∈ U − S } \{1(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S}这些观察激发了一种推导出收敛结果的通用技术
对于人们在实践中可能想要的 { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S}。首先,我们表明,在 S 元素(即 { H ( x ) : x ∈ S } \{H(x):\:x\in S\} {H(x):x∈S})使用的哈希位置集上,随机变量 { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} 本质上是独立的伯努利试验,成功概率为 lim n → ∞ \operatorname*{lim}_{n\to\infty} limn→∞Pr ( F ) (\mathcal{F}) (F) 。从技术角度来看,此结果是本节中最重要的。接下来,我们展示如何使用该结果来证明上述经典收敛定理的对应物,这些定理在我们的设置中成立正式进行,我们从关键定义开始。
定义 7.1.考虑任何
{
H
(
u
)
:
u
∈
U
}
\{H(u):u\in U\}
{H(u):u∈U} 是独立且同分布的方案。写入
S
=
{
x
1
,
…
,
x
n
}
S=\{x_{1},\ldots,x_{n}\}
S={x1,…,xn} .假阳性率定义为随机变量
R
=
P
r
(
F
∣
H
(
x
1
)
,
…
,
H
(
x
n
)
)
.
R=\mathbf{Pr}(\mathcal{F}\mid H(x_1),\ldots,H(x_n)).
R=Pr(F∣H(x1),…,H(xn)).
假阳性率得名于以下事实:以 R R R 为条件,随机变量 { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} 是具有共同成功概率的独立伯努利试验。 R R R .因此,对 U − S U-S U−S 元素的大量查询对过滤器的查询返回误报的分数很可能接近 $R $ 。从这个意义上说, R R R 虽然是一个随机变量,但其作用类似于 { 1 ( F ( z ) ) \{ \mathbf{1} ( \mathcal{F} ( z) ) {1(F(z)) : z ∈ U − S } z\in U- S\} z∈U−S} 的速率 重要的是要注意,在许多关于标准 Bloom 滤波器的文献中,假
阳性率的定义并非如上。相反,该术语通常用作假阳性概率的同义词。事实上,对于标准的布隆滤波器,我们定义的两个概念之间的区别在实践中并不重要,因为如第 2 节所述,可以很容易地证明 R . R. R. 非常接近 Pr ( F ) \Pr(\mathcal{F}) Pr(F),概率极高(例如,参见 [11])。事实证明,这个结果非常自然地推广到本文提出的框架,因此即使在我们非常一般的环境中,这两个概念之间的实际差异在很大程度上也并不重要。但是,证明比标准 Bloom 过滤器的情况更复杂,因此我们将非常小心地使用我们定义的术语。
定理 7.1.考虑一个引理 4.1 的条件成立的方案。此外,假设存在一些函数 y y y 和独立的同分布随机变量。 { V u : u ∈ U } \{V_{u}:u\in U\} {Vu:u∈U} ,使得 V u V_{u} Vu 在 Supp ( V u ) \operatorname{Supp}(V_{u}) Supp(Vu) 上是均匀的,而对于 u ∈ U u\in U u∈U ,我们有 H ( u ) = g ( V u ) H(u)=g(V_{u}) H(u)=g(Vu)定义
p = d e f ( 1 − e − λ / k ) k Δ = d e f max i ∈ H P r ( i ∈ H ( u ) ) − λ n k ( = o ( 1 / n ) ) ξ = d e f n k Δ ( 2 λ + k Δ ) ( = o ( 1 ) ) \begin{aligned}&p\stackrel{def}{=}\left(1-\mathrm{e}^{-\lambda/k}\right)^{k}\\&\Delta\stackrel{def}{=}\max_{i\in H}\mathbf{Pr}(i\in H(u))-\frac{\lambda}{nk}\quad(=o(1/n))\\&\xi\stackrel{def}{=}nk\Delta(2\lambda+k\Delta)\quad(=o(1))\end{aligned} p=def(1−e−λ/k)kΔ=defi∈HmaxPr(i∈H(u))−nkλ(=o(1/n))ξ=defnkΔ(2λ+kΔ)(=o(1))
然后对于任何 ϵ = ϵ ( n ) > 0 \epsilon=\epsilon(n)>0 ϵ=ϵ(n)>0 和 ϵ = ω ( ∣ P r ( F ) − p ∣ ) \epsilon=\omega(|\mathbf{Pr}(\mathcal{F})-p|) ϵ=ω(∣Pr(F)−p∣) ,for n 足够大,使得 ϵ > ∣ Pr ( F ) − p ∣ \epsilon>|\Pr(\mathcal{F})-p| ϵ>∣Pr(F)−p∣
P r ( ∣ R − p ∣ > ϵ ) ≤ 2 exp [ − 2 n ( ϵ − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] . \mathbf{Pr}(|R-p|>\epsilon)\leq2\exp\left[\frac{-2n(\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)^{2}}{\lambda^{2}+\xi}\right]. Pr(∣R−p∣>ϵ)≤2exp[λ2+ξ−2n(ϵ−∣Pr(F)−p∣)2].
此外,对于任何功能。 h ( n ) h( n) h(n) = o ( min ( 1 / ∣ P r ( F ) o( \operatorname* { min} ( 1/ | \mathbf{Pr}( \mathcal{F} ) o(min(1/∣Pr(F) − p ∣ , n ) ) - p| , \sqrt {n}) ) −p∣,n)) ,我们有 ( R − p ) h ( n ) (R-p)h(n) (R−p)h(n) 收敛到 0 的概率为 T l → x Tl\rightarrow\mathbf{x} Tl→x
备注。由于引理 4.1 的 ∣ P r ( F ) − p ∣ = o ( 1 ) \left|\mathbf{Pr}(\mathcal{F})-p\right|=o(1) ∣Pr(F)−p∣=o(1),我们可以在定理 7.1 中采用 h ( n ) = 1 h(n)=1 h(n)=1 来得出结论, R R R 收敛到 P P P 的概率为 T l → ∞ Tl\to\infty Tl→∞
从定理 5.1 和 5.2 的证明中,很容易看出,对于分区和(扩展的)双重哈希方案, Δ = 0 \Delta=0 Δ=0 SO ξ = 0 \xi=0 ξ=0 对于这两个方案也是如此
备注。我们在 H ( u ) H(u) H(u) 的分布上添加了一个新条件,但它在本文中讨论的所有方案中都微不足道(因为,对于独立的完全随机哈希函数 h 1 h_{1} h1 和 h 2 h_{2} h2 ,随机变量 { ( h 1 ( u ) , h 2 ( u ) ) : \{ ( h_{1}( u) , h_{2}( u) ) : {(h1(u),h2(u)): u ∈ U } u\in U\} u∈U} 是独立的并且是同分布的, 和 ( h 1 ( u ) , h 2 ( u ) ) (h_{1}(u),h_{2}(u)) (h1(u),h2(u)) 均匀分布在其支持上)。
证明。该证明本质上是将 Azuma 不等式的标准应用于适当定义的 Doob 马丁格尔。具体来说,我们采用 [12, Section 12.5] 中讨论的技术为方便起见,写 S = { x 1 , … , x n } S=\{x_{1},\ldots,x_{n}\} S={x1,…,xn} 。对于 h 1 , … , h n ∈ h_{1},\ldots,h_{n}\in h1,…,hn∈Supp ( H ( u ) ) (H(u)) (H(u)) ,定义
f ( h 1 , … , h n ) = d e f P r ( F ∣ H ( x 1 ) = h 1 , … , H ( x n ) = h n ) , f(h_1,\ldots,h_n)\stackrel{\mathrm{def}}{=}\mathbf{Pr}(\mathcal{F}\mid H(x_1)=h_1,\ldots,H(x_n)=h_n), f(h1,…,hn)=defPr(F∣H(x1)=h1,…,H(xn)=hn),
并注意 R = f ( H ( x 1 ) , … , H ( x n ) ) R=f(H(x_{1}),\ldots,H(x_{n})) R=f(H(x1),…,H(xn)) 。现在考虑一些 C C C,使得对于任何 h 1 , … , h j h_{1},\ldots,h_{j} h1,…,hj , h j ′ h_{j}^{\prime} hj′ h j + 1 , … , h n ∈ h_{j+1},\ldots,h_{n}\in hj+1,…,hn∈Supp ( H ( u ) ) (H(u)) (H(u))
∣ f ( h 1 , … , h n ) − f ( h 1 , … , h j − 1 , h j ′ , h j + 1 , … , h n ) ∣ ≤ c . |f(h_1,\dots,h_n)-f(h_1,\dots,h_{j-1},h_j',h_{j+1},\dots,h_n)|\leq c. ∣f(h1,…,hn)−f(h1,…,hj−1,hj′,hj+1,…,hn)∣≤c.
由于 H ( x i ) H(x_{i}) H(xi) 是独立的,我们可以应用 [12, Section 12.5] 的结果来获得
P r ( ∣ R − E [ R ] ∣ ≥ δ ) ≤ 2 e − 2 δ 2 / n c 2 , \mathbf{Pr}(|R-\mathbf{E}[R]|\geq\delta)\leq2\mathrm{e}^{-2\delta^{2}/nc^{2}}, Pr(∣R−E[R]∣≥δ)≤2e−2δ2/nc2,
对于任何 δ > 0 \delta>0 δ>0
要找到 t t t wewrite 的小选择
∣ f ( h 1 , … , h n ) − f ( h 1 , … , h j − 1 , h j ′ , h j + 1 , … , h n ) ∣ = ∣ Pr ( F ∣ H ( x 1 ) = h 1 , … , H ( x n ) = h n ) − Pr ( F ∣ H ( x 1 ) = h 1 , … , H ( x j − 1 ) = h j − 1 , H ( x j ) = h j ′ , H ( x j + 1 ) = h j + 1 , … H ( x n ) = ∣ ∣ { v ∈ S u p p ( V u ) : g ( v ) ⊆ ⋃ i = 1 n h i } ∣ − ∣ { v ∈ S u p p ( V u ) : g ( v ) ⊆ ⋃ i = 1 n { h j ′ i = j h i i ≠ j } ∣ ∣ S u p p ( V u ) ∣ ≤ max v ′ ∈ S u p p ( V u ) ∣ { v ∈ S u p p ( V u ) : ∣ g ( v ) ∩ g ( v ′ ) ∣ ≥ 1 } ∣ ∣ S u p p ( V u ) ∣ = max M ′ ∈ S u p p ( H ( u ) ) P r ( ∣ H ( u ) ∩ M ′ ∣ ≥ 1 ) , \left.\begin{aligned}&\left|f(h_{1},\ldots,h_{n})-f(h_{1},\ldots,h_{j-1},h_{j}^{\prime},h_{j+1},\ldots,h_{n})\right|\\&=\left|\Pr(\mathcal{F}\mid H(x_{1})=h_{1},\ldots,H(x_{n})=h_{n})\right.\\&-\Pr(\mathcal{F}\mid H(x_{1})=h_{1},\ldots,H(x_{j-1})=h_{j-1},H(x_{j})=h_{j}^{\prime},H(x_{j+1})=h_{j+1},\ldots H(x_{n})\\&=\frac{\left|\left|\{v\in\mathrm{Supp}(V_u):g(v)\subseteq\bigcup_{i=1}^nh_i\}\right|-\left|\left\{v\in\mathrm{Supp}(V_u):g(v)\subseteq\bigcup_{i=1}^n\left\{\begin{array}{c}h_j^{\prime}&i=j\\h_i&i\neq j\end{array}\right.\right.\right\}\right|}{\left|\mathrm{Supp}(V_u)\right|}\\&\leq\frac{\max_{v^{\prime}\in\mathrm{Supp}(V_u)}\mid\{v\in\mathrm{Supp}(V_u):|g(v)\cap g(v^{\prime})|\geq1\}\mid}{\left|\mathrm{Supp}(V_u)\right|}\\&=\max_{M^{\prime}\in\mathrm{Supp}(H(u))}\mathbf{Pr}(|H(u)\cap M^{\prime}|\geq1),\end{aligned}\right. f(h1,…,hn)−f(h1,…,hj−1,hj′,hj+1,…,hn) =∣Pr(F∣H(x1)=h1,…,H(xn)=hn)−Pr(F∣H(x1)=h1,…,H(xj−1)=hj−1,H(xj)=hj′,H(xj+1)=hj+1,…H(xn)=∣Supp(Vu)∣ ∣{v∈Supp(Vu):g(v)⊆⋃i=1nhi}∣− {v∈Supp(Vu):g(v)⊆⋃i=1n{hj′hii=ji=j} ≤∣Supp(Vu)∣maxv′∈Supp(Vu)∣{v∈Supp(Vu):∣g(v)∩g(v′)∣≥1}∣=M′∈Supp(H(u))maxPr(∣H(u)∩M′∣≥1),
其中第一步只是 f f f 的定义,第二步是从 V u V_{u} Vu 和 y y y 的定义开始,第三步成立,因为将 h i h_{i} hi 之一更改为某个 M ′ ∈ Supp ( H ( u ) ) M^{\prime}\in\operatorname{Supp}(H(u)) M′∈Supp(H(u)) 无法更改
∣ { v ∈ Supp ( V u ) : g ( v ) ⊆ ⋃ i = 1 n h i } ∣ \left|\left\{v\in\operatorname{Supp}(V_u)\::\:g(v)\subseteq\bigcup\limits_{i=1}^nh_i\right\}\right| {v∈Supp(Vu):g(v)⊆i=1⋃nhi}
bv 超过
∣ { v ∈ S u p p ( V u ) : ∣ g ( v ) ∩ M ′ ∣ ≥ 1 } ∣ , \left|\left\{v\in\mathrm{Supp}(V_u)\::\:|g(v)\cap M'|\geq1\right\}\right|, ∣{v∈Supp(Vu):∣g(v)∩M′∣≥1}∣,
第四步来自 V u V_{u} Vu 和 y y y 的定义
现在考虑任何固定 M ′ ∈ Supp ( H ( u ) ) M^{\prime}\in\operatorname{Supp}(H(u)) M′∈Supp(H(u)) ,并设 y 1 , … , y ∣ M ′ ∣ y_{1},\ldots,y_{|M^{\prime}|} y1,…,y∣M′∣ 是 M ′ M^{\prime} M′ 的不同元素。回想一下 ∥ M ′ ∥ = k \|M^{\prime}\|=k ∥M′∥=k ,SO ∣ M ′ ∣ ≤ k |M^{\prime}|\leq k ∣M′∣≤k .应用一个联合 bound,我们有那个
P r ( ∣ H ( u ) ∩ M ′ ∣ ≥ 1 ) = P r ( ⋃ i = 1 ∣ M ′ ∣ y i ∈ H ( u ) ) ≤ ∑ i = 1 ∣ M ′ ∣ P r ( y i ∈ H ( u ) ) ≤ ∑ i = 1 ∣ M ′ ∣ λ k n + Δ ≤ λ n + k Δ . \begin{aligned}\mathbf{Pr}(|H(u)\cap M'|\geq1)&=\mathbf{Pr}\left(\bigcup_{i=1}^{|M^{\prime}|}y_{i}\in H(u)\right)\\&\leq\sum_{i=1}^{|M^{\prime}|}\mathbf{Pr}(y_{i}\in H(u))\\&\leq\sum_{i=1}^{|M^{\prime}|}\frac{\lambda}{kn}+\Delta\\&\leq\frac{\lambda}{n}+k\Delta.\end{aligned} Pr(∣H(u)∩M′∣≥1)=Pr i=1⋃∣M′∣yi∈H(u) ≤i=1∑∣M′∣Pr(yi∈H(u))≤i=1∑∣M′∣knλ+Δ≤nλ+kΔ.
因此,我们可以设置 c = λ n + k Δ c=\frac{\lambda}{n}+k\Delta c=nλ+kΔ 来获取
P r ( ∣ R − E [ R ] ∣ > δ ) ≤ 2 exp [ − 2 n δ 2 λ 2 + ξ ] , \mathbf{Pr}(|R-\mathbf{E}[R]|>\delta)\leq2\exp\left[\frac{-2n\delta^2}{\lambda^2+\xi}\right], Pr(∣R−E[R]∣>δ)≤2exp[λ2+ξ−2nδ2],
对于任何 δ > 0 \delta>0 δ>0 .由于 E [ R ] = \mathbf{E}[R]= E[R]=Pr ( F ) (\mathcal{F}) (F) ,我们写(对于足够大的 T l . Tl. Tl.,使得 ϵ > ∣ P r ( F ) − p ∣ ) \epsilon>|\mathbf{Pr}(\mathcal{F})-p|) ϵ>∣Pr(F)−p∣)
P r ( ∣ R − p ∣ > ϵ ) ≤ P r ( ∣ R − P r ( F ) ∣ > ϵ − ∣ P r ( F ) − p ∣ ) ≤ 2 exp [ − 2 n ( ϵ − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] . \begin{aligned}\mathbf{Pr}(|R-p|>\epsilon)&\leq\mathbf{Pr}(|R-\mathbf{Pr}(\mathcal{F})|>\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)\\&\leq2\exp\left[\frac{-2n(\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)^2}{\lambda^2+\xi}\right].\end{aligned} Pr(∣R−p∣>ϵ)≤Pr(∣R−Pr(F)∣>ϵ−∣Pr(F)−p∣)≤2exp[λ2+ξ−2n(ϵ−∣Pr(F)−p∣)2].
为了完成证明,我们看到对于任何常数 δ > 0 \delta>0 δ>0
P r ( ∣ R − p ∣ h ( n ) > δ ) = P r ( ∣ R − p ∣ > δ / h ( n ) ) → 0 a s n → ∞ , \mathbf{Pr}(|R-p|h(n)>\delta)=\mathbf{Pr}(|R-p|>\delta/h(n))\to0\quad\mathrm{as}\:n\to\infty, Pr(∣R−p∣h(n)>δ)=Pr(∣R−p∣>δ/h(n))→0asn→∞,
其中第二步来自 ∣ P r ( F ) − p ∣ = o ( 1 / h ( n ) ) |\mathbf{Pr}(\mathcal{F})-p|=o(1/h(n)) ∣Pr(F)−p∣=o(1/h(n)) 的事实,因此足够大 77。,
P r ( ∣ R − p ∣ > δ / h ( n ) ) ≤ 2 exp [ − 2 n ( δ / h ( n ) − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] ≤ 2 exp [ − δ 2 λ 2 + ξ ⋅ n h ( n ) 2 ] → 0 a s n → ∞ , \begin{aligned}\mathbf{Pr}(|R-p|>\delta/h(n))&\leq2\exp\left[\frac{-2n(\delta/h(n)-|\mathbf{Pr}(\mathcal{F})-p|)^{2}}{\lambda^{2}+\xi}\right]\\&\leq2\exp\left[-\frac{\delta^{2}}{\lambda^{2}+\xi}\cdot\frac{n}{h(n)^{2}}\right]\\&\to0\quad\mathrm{as}\:n\to\infty,\end{aligned} Pr(∣R−p∣>δ/h(n))≤2exp[λ2+ξ−2n(δ/h(n)−∣Pr(F)−p∣)2]≤2exp[−λ2+ξδ2⋅h(n)2n]→0asn→∞,
最后一步是 h ( n ) = o ( n ) h(n)=o({\sqrt{n}}) h(n)=o(n)
由于以 R . R. R. 为条件,事件 { F ( z ) : z ∈ U − S } \{{\mathcal{F}}(z):z\in U-S\} {F(z):z∈U−S} 是独立的,并且每个事件的发生概率都 R . R. R. ,定理 7.1 表明 { 1 ( F ( z ) ) : z ∈ U − S } \{\mathbf{1}(\mathcal{F}(z)):z\in U-S\} {1(F(z)):z∈U−S} 本质上是独立的伯努利试验,成功概率为 μ̸ \not{\mu} μ 。下一个结果是这个想法的正式化。
引理 7.1.考虑一个定理 7.1 的条件成立的方案。设 F n 0 ( z ) \mathcal{F}_{n_0}(z) Fn0(z) 表示 F ( z ) \mathcal{F}(z) F(z) 在方案与 η l = η 0 \eta_{l}=\eta_{0} ηl=η0 一起使用的情况下表示 F ( z ) \mathcal{F}(z) F(z) 。同样,在 T l = Y l 0 {\boldsymbol{T}\boldsymbol{l}}={\boldsymbol{Y}\boldsymbol{l}}_{0} Tl=Yl0 的情况下,让 R n 0 R_{n_0} Rn0 表示 R R R。设 { X n } \{X_{n}\} {Xn} 是实值随机变量序列,其中每个变量。 X n X_{n} Xn 可以被理解为 { 1 ( F n ( z ) ) 的某个函数 : \{ \mathbf{1} ( \mathcal{F} _{n}( z) ) 的某个函数 : {1(Fn(z))的某个函数: z ∈ U − S } z\in U- S\} z∈U−S} ,并设 Y Y Y 是 1 R 1\mathbb{R} 1R 上的任何概率分布。然后对于每个 x ∈ R x\in\mathbb{R} x∈R 和 ϵ = ϵ ( n ) > 0 \epsilon=\epsilon(n)>0 ϵ=ϵ(n)>0 和 ϵ = ω ( ∣ P r ( F ) − p ∣ ) \epsilon=\omega(|\mathbf{Pr}(\mathcal{F})-p|) ϵ=ω(∣Pr(F)−p∣) ,对于足够大的 T I TI TI,使得 ϵ > ∣ Pr ( F ) − p ∣ \epsilon>\left|\Pr(\mathcal{F})-p\right| ϵ>∣Pr(F)−p∣
∣ Pr ( X n ≤ x ) − Pr ( Y ≤ x ) ∣ ≤ ∣ Pr ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) − Pr ( Y ≤ x ) ∣ + 2 exp [ − 2 n ( ϵ − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] . \begin{aligned}|\Pr(X_{n}\leq x)-\Pr(Y\leq x)|\leq|\Pr(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)-\Pr(Y\leq x)|\\&+2\exp\left[\frac{-2n(\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)^{2}}{\lambda^{2}+\xi}\right].\end{aligned} ∣Pr(Xn≤x)−Pr(Y≤x)∣≤∣Pr(Xn≤x∣∣Rn−p∣≤ϵ)−Pr(Y≤x)∣+2exp[λ2+ξ−2n(ϵ−∣Pr(F)−p∣)2].
证明。证明是定理 7.1.fix any x ∈ x\in x∈ 18 ,并选择一些满足引理条件的 E E E。Ther.
n ≤ x ) = P r ( X n ≤ x , ∣ R n − p ∣ > ϵ ) + P r ( X n ≤ x , ∣ R n − p ∣ ≤ ϵ ) = P r ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) + P r ( ∣ R n − p ∣ > ϵ ) [ P r ( X n ≤ x ∣ ∣ R n − p ∣ > ϵ ) − P r ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ] \begin{aligned}{}_{n}\leq x)&=\mathbf{Pr}(X_{n}\leq x,|R_{n}-p|>\epsilon)+\mathbf{Pr}(X_{n}\leq x,|R_{n}-p|\leq\epsilon)\\&=\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)\\&+\mathbf{Pr}(|R_{n}-p|>\epsilon)\left[\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|>\epsilon)-\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon\right]\end{aligned} n≤x)=Pr(Xn≤x,∣Rn−p∣>ϵ)+Pr(Xn≤x,∣Rn−p∣≤ϵ)=Pr(Xn≤x∣∣Rn−p∣≤ϵ)+Pr(∣Rn−p∣>ϵ)[Pr(Xn≤x∣∣Rn−p∣>ϵ)−Pr(Xn≤x∣∣Rn−p∣≤ϵ]
这意味着
∣ Pr ( X n ≤ x ) − Pr ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) ∣ ≤ Pr ( ∣ R n − p ∣ > ϵ ) . |\Pr(X_n\leq x)-\Pr(X_n\leq x\mid|R_n-p|\leq\epsilon)|\leq\Pr(|R_n-p|>\epsilon). ∣Pr(Xn≤x)−Pr(Xn≤x∣∣Rn−p∣≤ϵ)∣≤Pr(∣Rn−p∣>ϵ).
因此
( X n ≤ x ) − P r ( Y ≤ x ) ∣ P r ( X n ≤ x ) − P r ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) ∣ + ∣ P r ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) − P r ( Y n ≤ x ) P r ( ∣ R n − p ∣ > ϵ ) + ∣ P r ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) − P r ( Y n ≤ x ) ∣ , \begin{aligned}&(X_{n}\leq x)-\mathbf{Pr}(Y\leq x)|\\&\mathbf{Pr}(X_{n}\leq x)-\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)|+|\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)-\mathbf{Pr}(Y_{n}\leq x)\\&\mathbf{Pr}(|R_{n}-p|>\epsilon)+|\mathbf{Pr}(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)-\mathbf{Pr}(Y_{n}\leq x)|,\end{aligned} (Xn≤x)−Pr(Y≤x)∣Pr(Xn≤x)−Pr(Xn≤x∣∣Rn−p∣≤ϵ)∣+∣Pr(Xn≤x∣∣Rn−p∣≤ϵ)−Pr(Yn≤x)Pr(∣Rn−p∣>ϵ)+∣Pr(Xn≤x∣∣Rn−p∣≤ϵ)−Pr(Yn≤x)∣,
因此,对于足够大的 T l . Tl. Tl.,使得 ϵ > ∣ P r ( F ) − p ∣ \epsilon>\left|\mathbf{Pr}(\mathcal{F})-p\right| ϵ>∣Pr(F)−p∣
∣ Pr ( X n ≤ x ) − Pr ( Y ≤ x ) ∣ ≤ ∣ Pr ( X n ≤ x ∣ ∣ R n − p ∣ ≤ ϵ ) − Pr ( Y ≤ x ) ∣ + 2 exp [ − 2 n ( ϵ − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] , \begin{aligned}|\Pr(X_{n}\leq x)-\Pr(Y\leq x)|\leq|\Pr(X_{n}\leq x\mid|R_{n}-p|\leq\epsilon)-\Pr(Y\leq x)|\\&+2\exp\left[\frac{-2n(\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)^{2}}{\lambda^{2}+\xi}\right],\end{aligned} ∣Pr(Xn≤x)−Pr(Y≤x)∣≤∣Pr(Xn≤x∣∣Rn−p∣≤ϵ)−Pr(Y≤x)∣+2exp[λ2+ξ−2n(ϵ−∣Pr(F)−p∣)2],
由 Theorem 7.1 提供。
通过阐述定理 7.1 和引理 7.1 的强大功能,我们用它们来证明大数强定律的版本。Hoeffding 不等式和中心极限定理。
定理 7.2.考虑一个满足定理条件的方案 7.1.设 Z ⊆ U − S Z\subseteq U-S Z⊆U−S 是可数无限的,并写成 Z = { z 1 , z 2 , … } Z=\{z_{1},z_{2},\ldots\} Z={z1,z2,…} 。然后对于任何 ϵ > 0 \epsilon>0 ϵ>0 ,对于 n 足够大,使得 ϵ > ∣ P r ( F ) − p ∣ \epsilon>\left|\mathbf{Pr}(\mathcal{F})-p\right| ϵ>∣Pr(F)−p∣ ,我们有。
Pr ( lim ℓ → ∞ 1 ℓ ∑ i = 1 ℓ 1 ( F n ( z i ) ) = R n ) = 1. \Pr\left(\lim\limits_{\ell\to\infty}\dfrac{1}{\ell}\sum\limits_{i=1}^{\ell}\mathbf{1}(\mathcal{F}_{n}(z_{i}))=R_{n}\right)=1. Pr(ℓ→∞limℓ1i=1∑ℓ1(Fn(zi))=Rn)=1.
2.对于任何 ϵ > 0 \epsilon>0 ϵ>0 ,对于 TI 足够大,使得 ϵ > ∣ Pr ( F ) − p ∣ \epsilon>\left|\Pr(\mathcal{F})-p\right| ϵ>∣Pr(F)−p∣
P r ( ∣ lim ℓ → ∞ 1 ℓ ∑ i = 1 ℓ 1 ( F n ( z i ) ) − p ∣ > ϵ ) ≤ 2 exp [ − 2 n ( ϵ − ∣ P r ( F ) − p ∣ ) 2 λ 2 + ξ ] . \mathbf{Pr}\left(\left|\lim\limits_{\ell\to\infty}\dfrac{1}{\ell}\sum\limits_{i=1}^\ell\mathbf{1}(\mathcal{F}_n(z_i))-p\right|>\epsilon\right)\leq2\exp\left[\dfrac{-2n(\epsilon-|\mathbf{Pr}(\mathcal{F})-p|)^2}{\lambda^2+\xi}\right]. Pr( ℓ→∞limℓ1i=1∑ℓ1(Fn(zi))−p >ϵ)≤2exp[λ2+ξ−2n(ϵ−∣Pr(F)−p∣)2].
特别是, lim ℓ → ∞ 1 ℓ ∑ i = 1 ℓ 1 ( F n ( z i ) ) \operatorname*{lim}_{\ell\rightarrow\infty}\frac1\ell\sum_{i=1}^\ell\mathbf{1}(\mathcal{F}_n(z_i)) limℓ→∞ℓ1∑i=1ℓ1(Fn(zi)) 收敛到 P P P 的概率为 7 l → 0 7l\rightarrow0 7l→0
3.对于任何函数 Q ( n ) Q(n) Q(n) , ϵ > 0 \epsilon>0 ϵ>0 ,andn 足够大,使得 ϵ / 2 > ∣ P r ( F ) − p ∣ \epsilon/2>\left|\mathbf{Pr}(\mathcal{F})-p\right| ϵ/2>∣Pr(F)−p∣
公关
r
(
∣
1
Q
(
n
)
∑
i
=
1
Q
(
n
)
1
(
F
n
(
z
i
)
)
−
p
∣
>
ϵ
)
≤
2
e
−
Q
(
n
)
ϵ
2
/
2
+
2
exp
[
−
2
n
(
ϵ
/
2
−
∣
P
r
(
F
)
−
p
∣
)
2
λ
2
+
ξ
]
.
\mathbf{r}\left(\left|{\frac{1}{Q(n)}}\sum_{i=1}^{Q(n)}\mathbf{1}(\mathcal{F}_{n}(z_{i}))-p\right|>\epsilon\right)\leq2\mathrm{e}^{-Q(n)\epsilon^{2}/2}+2\exp\left[{\frac{-2n(\epsilon/2-|\mathbf{Pr}(\mathcal{F})-p|)^{2}}{\lambda^{2}+\xi}}\right].
r
Q(n)1i=1∑Q(n)1(Fn(zi))−p
>ϵ
≤2e−Q(n)ϵ2/2+2exp[λ2+ξ−2n(ϵ/2−∣Pr(F)−p∣)2].
4.对于任何函数 Q ( n ) Q(n) Q(n) 和 lim n → ∞ Q ( n ) = ∞ \operatorname*{lim}_{n\to\infty}Q(n)=\infty limn→∞Q(n)=∞ 且 Q ( n ) = o ( min ( 1 / ∣ P r ( F ) − p ∣ 2 , n ) ) Q(n)=o(\operatorname*{min}(1/|\mathbf{Pr}(\mathcal{F})-p|^{2},n)) Q(n)=o(min(1/∣Pr(F)−p∣2,n))
∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) − p Q ( n ) p ( 1 − p ) → \sum_{i=1}^{Q(n)}\frac{\mathbf{1}(\mathcal{F}_{n}(z_{i}))-p}{\sqrt{Q(n)p(1-p)}}\to ∑i=1Q(n)Q(n)p(1−p)1(Fn(zi))−p→N(0,1) in itituin s 7 l → 0 7l\rightarrow0 7l→0
备注。根据定理 6.2 和 6.3,对于第 5 节中介绍的分区和双重哈希方案, ∣ P r ( F ) − p ∣ = Θ ( 1 / n ) |\mathbf{Pr}(\mathcal{F})-p|=\Theta(1/n) ∣Pr(F)−p∣=Θ(1/n)。因此,对于每个方案,定理 7.2 第四部分中的条件 Q ( n ) = Q(n)= Q(n)= o ( min ( 1 / ∣ P r ( F ) − p ∣ 2 , n ) ) o(\operatorname*{min}(1/|\mathbf{Pr}(\mathcal{F})-p|^{2},n)) o(min(1/∣Pr(F)−p∣2,n)) 变为 Q ( n ) = o ( n ) Q(n)=o(n) Q(n)=o(n)
证明。由于给定 R n R_{n} Rn ,随机变量 { 1 ( F n ( z ) ) : z ∈ Z } \{\mathbf{1}(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn(z)):z∈Z} 是条件独立的伯努利试验,具有共同的成功概率 R n R_{n} Rn ,因此直接应用大数强定律会产生第一项。对于第二项,我们注意到第一项意味着
lim ℓ → ∞ 1 ℓ ∑ i = 1 ℓ 1 ( F n ( z i ) ) ∼ R n . \lim\limits_{\ell\to\infty}\frac{1}{\ell}\sum\limits_{i=1}^{\ell}\mathbf{1}(\mathcal{F}_{n}(z_{i}))\sim R_{n}. ℓ→∞limℓ1i=1∑ℓ1(Fn(zi))∼Rn.
然后直接应用定理 7.1 即可得出结果。
其余两项的难度略高。但是,可以使用 Lemma 7.1 的简单应用程序来处理它们。对于第三项,定义
X n = d e f ∣ 1 Q ( n ) ∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) − p ∣ . X_n\stackrel{\mathrm{def}}{=}\left|\frac{1}{Q(n)}\sum_{i=1}^{Q(n)}\mathbf{1}(\mathcal{F}_n(z_i))-p\right|. Xn=def Q(n)1i=1∑Q(n)1(Fn(zi))−p .
和 Y = d e t 0 Y\overset{\mathrm{det}}{\operatorname*{=}}0 Y=det0 。设 =e/2 得到
P r ( X n > ϵ ∣ ∣ R n − p ∣ ≤ δ ) = P r ( ∣ ∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) ) − Q ( n ) p ∣ > Q ( n ) ϵ ∣ ∣ R n − p ∣ ≤ δ ) ≤ P r ( ∣ ∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) − Q ( n ) R n ∣ > Q ( n ) ( ϵ − ∣ R n − p ∣ ) ∣ ∣ R n − p ∣ ≤ δ ) ≤ P r ( ∣ ∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) − Q ( n ) R n ∣ > Q ( n ) ϵ 2 ∣ ∣ R n − p ∣ ≤ δ ) ≤ 2 e − Q ( n ) t 2 / 2 , \begin{aligned}&\mathbf{Pr}(X_{n}>\epsilon\mid|R_{n}-p|\leq\delta)\\&=\mathbf{Pr}\left(\left|\sum_{i=1}^{Q(n)}\mathbf{1}(\mathcal{F}_{n}(z_{i})))-Q(n)p\right|>Q(n)\epsilon\:\bigg|\:|R_{n}-p|\leq\delta\right)\\&\leq\mathbf{Pr}\left(\left|\sum_{i=1}^{Q(n)}\mathbf{1}(\mathcal{F}_{n}(z_{i}))-Q(n)R_{n}\right|>Q(n)\left(\epsilon-|R_{n}-p|\right)\:\bigg|\:|R_{n}-p|\leq\delta\right)\\&\leq\mathbf{Pr}\left(\left|\sum_{i=1}^{Q(n)}\mathbf{1}(\mathcal{F}_{n}(z_{i}))-Q(n)R_{n}\right|>\frac{Q(n)\epsilon}{2}\:\bigg|\:|R_{n}-p|\leq\delta\right)\\&\leq2\mathrm{e}^{-Q(n)t^{2}/2},\end{aligned} Pr(Xn>ϵ∣∣Rn−p∣≤δ)=Pr i=1∑Q(n)1(Fn(zi)))−Q(n)p >Q(n)ϵ ∣Rn−p∣≤δ ≤Pr i=1∑Q(n)1(Fn(zi))−Q(n)Rn >Q(n)(ϵ−∣Rn−p∣) ∣Rn−p∣≤δ ≤Pr i=1∑Q(n)1(Fn(zi))−Q(n)Rn >2Q(n)ϵ ∣Rn−p∣≤δ ≤2e−Q(n)t2/2,
其中前两个步骤是显而易见的,第三步是 P r ( F n ∣ R n ) = R n \mathbf{Pr}(\mathcal{F}_{n}\mid R_{n})=R_{n} Pr(Fn∣Rn)=Rn 的事实,第四步是霍夫丁不等式的应用(利用以下事实:给定 R n R_{n} Rn { 1 ( F n ( z ) ) : z ∈ Z } \{1(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn(z)):z∈Z} 是独立且同分布的伯努利试验,共量成功概率为 R n R_{n} Rn )。
现在,由于 P r ( Y ≤ ϵ ) = 1 \mathbf{Pr}(Y\leq\epsilon)=1 Pr(Y≤ϵ)=1
P r ( X n ≤ ϵ ∣ ∣ R n − p ∣ ≤ δ ) − P r ( Y ≤ ϵ ) ∣ = P r ( X n > ϵ ∣ ∣ R n − p ∣ ≤ δ ) ≤ 2 e − Q ( n ) ϵ 2 / 2 . \mathbf{Pr}(X_{n}\leq\epsilon\mid|R_{n}-p|\leq\delta)-\mathbf{Pr}(Y\leq\epsilon)|=\mathbf{Pr}(X_{n}>\epsilon\mid|R_{n}-p|\leq\delta)\leq2\mathrm{e}^{-Q(n)\epsilon^{2}/2}. Pr(Xn≤ϵ∣∣Rn−p∣≤δ)−Pr(Y≤ϵ)∣=Pr(Xn>ϵ∣∣Rn−p∣≤δ)≤2e−Q(n)ϵ2/2.
引理 7.1 的应用程序现在给出了第三项。对于第四项,我们写成
Q(n) >
1
(
F
n
(
z
i
)
)
−
p
Q
(
n
)
p
(
1
−
p
)
=
R
n
(
1
−
R
n
)
p
(
1
−
p
)
(
∑
i
=
1
Q
(
n
)
1
(
F
n
(
z
i
)
)
−
R
n
Q
(
n
)
R
n
(
1
−
R
n
)
+
(
R
n
−
p
)
Q
(
n
)
R
n
(
1
−
R
n
)
)
\frac{\mathbf{1}(\mathcal{F}_n(z_i))-p}{\sqrt{Q(n)p(1-p)}}=\sqrt{\frac{R_n(1-R_n)}{p(1-p)}}\left(\sum_{i=1}^{Q(n)}\frac{\mathbf{1}(\mathcal{F}_n(z_i))-R_n}{\sqrt{Q(n)R_n(1-R_n)}}+(R_n-p)\sqrt{\frac{Q(n)}{R_n(1-R_n)}}\right)
Q(n)p(1−p)1(Fn(zi))−p=p(1−p)Rn(1−Rn)
i=1∑Q(n)Q(n)Rn(1−Rn)1(Fn(zi))−Rn+(Rn−p)Rn(1−Rn)Q(n)
根据中心极限定理,
∑ i = 1 Q ( n ) 1 ( F n ( z i ) ) − R n Q ( n ) R n ( 1 − R n ) → N ( 0 , 1 ) 在分布中 n → ∞ , \displaystyle\sum_{i=1}^{Q(n)}\frac{\mathbf{1}(\mathcal{F}_n(z_i))-R_n}{\sqrt{Q(n)R_n(1-R_n)}}\to\mathrm{N}(0,1)\quad\text{在分布中}n\to\infty, i=1∑Q(n)Q(n)Rn(1−Rn)1(Fn(zi))−Rn→N(0,1)在分布中n→∞,
因为,给定 R n R_{n} Rn , { 1 ( F n ( z ) ) : z ∈ Z } \{\mathbf{1}(\mathcal{F}_{n}(z)):z\in Z\} {1(Fn(z)):z∈Z} 是独立且同分布的伯努利试验,具有共同的成功概率 R n R_{n} Rn 。此外,根据定理 7.1, R n R_{n} Rn 的概率收敛为 F F F,即 T l → x Tl\rightarrow\mathbf{x} Tl→x,因此足以证明 ( R n − p ) Q ( n ) (R_{n}-p)\sqrt{Q(n)} (Rn−p)Q(n) 的概率收敛为 0,即 η b → x \eta_{b}\rightarrow\mathbf{x} ηb→x。但是 Q ( n ) = o ( min ( 1 / ∣ P r ( F ) − p ∣ , n ) ) \sqrt{Q(n)}=o(\operatorname*{min}(1/|\mathbf{Pr}(\mathcal{F})-p|,\sqrt{n})) Q(n)=o(min(1/∣Pr(F)−p∣,n)) ,所以定理 7.1 的另一个应用给出了结果。L
8. 实验
在本节中,我们实证评估了前几节的理论结果,以 7 l 7l 7l 的小值。我们对以下具体方案感兴趣:标准的 Bloom filter 方案、分区方案、双重哈希方案和扩展的双重哈希方案,其中 f ( i ) = i 2 f(i)=i^{2} f(i)=i2 和 f ( i ) = i 3 f(i)=i^{3} f(i)=i3 对于 c ∈ { 4 , 8 , 12 , 16 } c\in\{4,8,12,16\} c∈{4,8,12,16} ,我们执行以下操作。首先,计算 k ∈ { ⌊ c ln 2 ⌋ , ⌈ c ln 2 ⌉ } k\in\{\lfloor c\ln2\rfloor,\lceil c\ln2\rceil\} k∈{⌊cln2⌋,⌈cln2⌉} 的值
最小化 p = ( 1 − exp [ − k / c ] ) k p=(1-\exp[-k/c])^{k} p=(1−exp[−k/c])k .接下来,对于正在考虑的每个方案,重复以下过程 10,000 次:使用指定的值 7 l 7l 7l , C C C 实例化过滤器
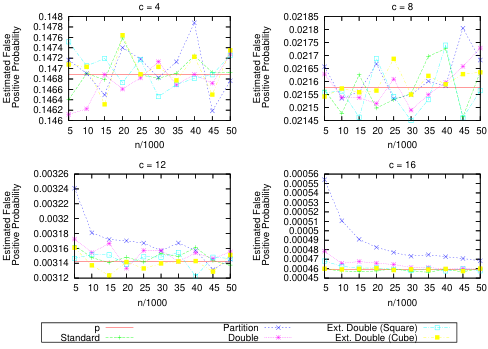
图 1:各种方案和参数的假阳性概率估计值。
和 k k k ,用一组 S S S 7 L 7L 7L 个项目填充过滤器,然后查询不在 S S S 中的 ⌈ 10 / p ⌉ \lceil10/p\rceil ⌈10/p⌉ 元素,记录过滤器返回误报的那些查询的 $Q $ 个。然后,我们通过对所有 10,000 次试验的结果求平均值来近似该方案的假阳性概率。此外,我们将试验结果按它们在 C Q CQ CQ 的值进行分箱,以检查 Q Q Q 分布的其他特征。
结果如图 1 和图 2 所示。在图 1 中,我们看到对于 C C C 的小值,不同的方案基本上彼此无法区分,同时具有接近 P P P 的假阳性概率/率。这个结果特别重要,因为我们正在试验的滤波器相当小,这支持了我们的说法,即即使在空间非常有限的环境中,这些方案也很有用。然而,我们也看到,对于稍大的 c ∈ { 12 , 16 } c\in\{12,16\} c∈{12,16} 值,分区方案不再特别有用 7 L 7L 7L 的小值,而其他方案则特别有用。这个结果并不特别令人惊讶,因为从第 6 节中我们知道,所有这些方案都不适合 T l . Tl. Tl. 的小值和 C \boldsymbol{C} C 的大值。此外,鉴于第 2 节中的观察结果,标准 Bloom 过滤器的分区版本的性能永远不会比原始版本更好,因此我们预计分区方案最不适合这些条件。尽管如此,分区方案在某些设置中可能仍然有用,因为它大大减少了哈希函数的范围。在图 2 中,我们给出了 n = 5000 n=5000 n=5000 和 c = 8 c=8 c=8 的实验结果的直方图
对于分区和扩展的双重哈希方案。请注意,对于 C C C 的这个值,优化 k k k 的结果是 k = 6 k=6 k=6 ,所以我们有 p ≈ 0.021577 p\approx0.021577 p≈0.021577 和 ⌈ 10 / p ⌉ = 464 \lceil10/p\rceil=464 ⌈10/p⌉=464 。在每个图中,我们将结果与 f = d e f 10 , 000 ϕ 464 p , 464 p ( 1 − p ) f\stackrel{\mathrm{def}}{=}10,000\phi_{464p,464p(1-p)} f=def10,000ϕ464p,464p(1−p) 进行比较,其中
ϕ μ , σ 2 ( x ) = d e f e − ( x − μ ) 2 / 2 σ 2 σ 2 π \phi_{\mu,\sigma^2}(x)\stackrel{\mathrm{def}}{=}\frac{\mathrm{e}^{-(x-\mu)^2/2\sigma^2}}{\sigma\sqrt{2\pi}} ϕμ,σ2(x)=defσ2πe−(x−μ)2/2σ2
表示 N ( μ , σ 2 ) {\mathrm{N}}(\mu,\sigma^{2}) N(μ,σ2) 的密度函数。正如人们所料,给定定理 7.2 第四部分的中心极限定理, f f f 为每个直方图提供了一个合理的近似值
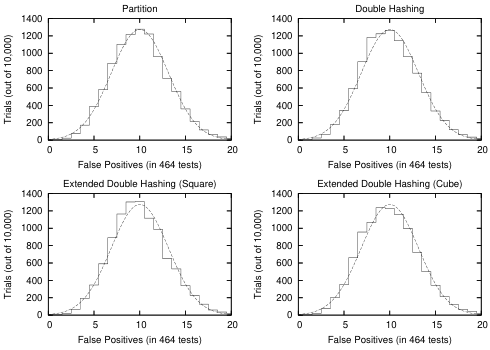
图 2: C Q CQ CQ 的分布估计( n = 5000 n=5000 n=5000 和 c = 8 c=8 c=8),与 $f $相比
9. 修改后的 Count-Min Sketch
现在,我们提出了对 [4] 中引入的 Count-Min Sketch的修改,它以类似于我们对 Bloom 过滤器的改进的方式使用更少的哈希函数,但代价是空间增加很小。我们首先回顾原始数据结构。
9.1 Count-Min Sketch 回顾
以下是对 [4] 中给出的描述的简要回顾。Count-Min Sketch将更新流 ( i t , c t ) (i_t,c_t) (it,ct) 作为输入,从 t = 1 t=1 t=1 开始,其中每个项目 i t i_{t} it 都是集合 U = { 1 , … , n } U=\{1,\ldots,n\} U={1,…,n} 的成员,每个计数 C t Ct Ct 都是一个正数。(可以扩展到负计数;我们在这里不考虑它们是为了方便。系统在时间 T T T 的状态由向量 a ⃗ ( T ) = ( a 1 ( T ) , … , a n ( T ) ) \vec{a}(T)=(a_{1}(T),\ldots,a_{n}(T)) a(T)=(a1(T),…,an(T)) 给出,其中 a j ( T ) a_{j}(T) aj(T) 是 t ≤ T t\leq T t≤T 和 i t = j i_{t}=j it=j 的所有 $Ct $ 的总和。当含义明确时,我们通常会去掉 I I I。Count-Min Sketch由宽度为 w = d e f ⌈ e / ϵ ⌉ w\stackrel{\mathrm{def}}{=}\left\lceil\mathrm{e}/\epsilon\right\rceil w=def⌈e/ϵ⌉ 和深度为 d = d e f ⌈ ln 1 / δ ⌉ d\stackrel{\mathrm{def}}{=}\left\lceil\ln1/\delta\right\rceil d=def⌈ln1/δ⌉ 的数组 Count 组成
计数 [ 1 , 1 ] , … [1,1],\ldots [1,1],…,计数 [ d , w ] [d,w] [d,w] .数组的每个条目都初始化为 U U U 。此外,CountMin Sketch使用独立于成对独立族 H H H 中选择的 d d d 哈希函数: { 1 , … , n } → { 1 , … , w } \{1,\ldots,n\}\to\{1,\ldots,w\} {1,…,n}→{1,…,w} Count-Min Sketch的机制非常简单。每当更新 ( i , c ) (i,c) (i,c)
到达时,我们将
C
o
u
n
t
[
j
,
h
j
(
i
)
]
\mathop{\mathrm{Count}}[j,h_{j}(i)]
Count[j,hj(i)] 增加
t
t
t 对于
j
=
1
,
…
,
d
j=1,\ldots,d
j=1,…,d 。每当我们想要
u
i
u_{i}
ui 的估计值(称为点查询)时,我们都会计算
a
^
i
=
d
e
f
min
j
=
1
d
C
o
u
n
t
[
j
,
h
j
(
i
)
]
.
\hat{a}_i\stackrel{\mathrm{def}}{=}\min_{j=1}^d\mathrm{Count}[j,h_j(i)].
a^i=defj=1mindCount[j,hj(i)].
Count-Min Sketch的基本结果是,对于每个
τ
˙
\dot{\tau}
τ˙
a
^
i
≥
a
a
n
d
P
r
(
a
^
i
≤
a
i
+
ϵ
∥
a
⃗
∥
)
≥
1
−
δ
,
\hat{a}_{i}\geq a\quad\mathrm{and}\quad\mathbf{Pr}(\hat{a}_{i}\leq a_{i}+\epsilon\|\vec{a}\|)\geq1-\delta,
a^i≥aandPr(a^i≤ai+ϵ∥a∥)≥1−δ,
其中 norm 是 L 1 L_{1} L1 范数。令人惊讶的是,这个非常简单的边界允许在 Count-Min Sketch上高效地实现许多复杂的估计程序。有关详细信息,请再次参考读者 [4]。
9.2使用更少的哈希函数
现在,我们将展示如何将本文前面讨论的布隆滤波器的改进有效地应用于 Count-Min Sketch。我们的修改保留了 Count-Min Sketch的所有基本功能,但将所需的成对独立哈希函数数量减少到 2 ⌈ ( ln 1 / δ ) / ( ln 1 / ϵ ) ⌉ 2\lceil(\ln1/\delta)/(\ln1/\epsilon)\rceil 2⌈(ln1/δ)/(ln1/ϵ)⌉ 。我们预计,在许多情况下, E E E 和 δ \delta δ 将是相关的,因此只需要恒定数量的哈希函数;事实上,在许多此类情况下,只需要两个哈希函数。我们描述了 Count-Min Sketch的一个变体,它只使用两个成对独立的哈希值
功能并保证
a ^ i ≥ a a n d P r ( a ^ i ≤ a i + ϵ ∥ a ⃗ ∥ ) ≥ 1 − ϵ . \hat{a}_{i}\geq a\quad\mathrm{and}\quad\mathbf{Pr}(\hat{a}_{i}\leq a_{i}+\epsilon\|\vec{a}\|)\geq1-\epsilon. a^i≥aandPr(a^i≤ai+ϵ∥a∥)≥1−ϵ.
鉴于这样的结果,使用 2 ⌈ ( ln 1 / δ ) / ( ln 1 / ϵ ) ⌉ 2\lceil(\ln1/\delta)/(\ln1/\epsilon)\rceil 2⌈(ln1/δ)/(ln1/ϵ)⌉ 成对独立哈希函数并实现所需的失败概率 δ \delta δ 的变体是很简单的:只需构建此数据结构的 2 ⌈ ( ln 1 / δ ) / ( ln 1 / ϵ ) ⌉ 2\lceil(\ln1/\delta)/(\ln1/\epsilon)\rceil 2⌈(ln1/δ)/(ln1/ϵ)⌉ 个独立副本,并始终使用其中一个副本给出的最小估计值来回答点查询。我们的变体将使用编号为 { 0 , 1 , … , d − 1 } \{0,1,\ldots,d-1\} {0,1,…,d−1} 的 d d d 个表,每个表都有正好 u b ub ub 个计数器
编号为 { 0 , 1 , … , w − 1 } \{0,1,\ldots,w-1\} {0,1,…,w−1} ,其中 d d d 和 U D UD UD 将在后面指定。我们坚持 $ub $ 为素数。就像在原始的 Count-Min Sketch中一样,我们让 Count [ j , k ] \operatorname{Count}[j,k] Count[j,k] 表示第 j j j 个表中第 k k k 个计数器的值。我们选择哈希函数 h 1 h_{1} h1 和 h 2 h_{2} h2 独立于成对独立函数。家族 H : { 0 , … , n − 1 } {\mathcal{H} }: \{ 0, \ldots , n- 1\} H:{0,…,n−1} → \to → { 0 , 1 , … , w − 1 } \{ 0, 1, \ldots , w- 1\} {0,1,…,w−1} ,并定义 $ g_{j}( x) $ = h 1 ( x ) h_{1}( x) h1(x) + j h 2 ( x ) jh_{2}( x) jh2(x) mod U U U for j = 0 , … , d − 1 j=0,\ldots,d-1 j=0,…,d−1 我们的数据结构的机制与原始的 Count-Min Sketch相同。
每当流中发生更新 ( i , c ) (i,c) (i,c) 时,我们就会将 C o u n t [ j , g j ( i ) ] \mathop{\mathrm{Count}}[j,g_{j}(i)] Count[j,gj(i)] 增加 t t t ,对于 j = j= j= $ $ 0,\ldots,d-1$ 。每当我们想要 u i u_{i} ui 的估计值时,我们都会计算
a ^ i = d e f min j = 0 d − 1 C o u n t [ j , g j ( i ) ] . \hat{a}_i\stackrel{\mathrm{def}}{=}\min\limits_{j=0}^{d-1}\mathrm{Count}[j,g_j(i)]. a^i=defj=0mind−1Count[j,gj(i)].
我们证明了以下结果:
定理 9.1.对于上述 Count-Min Sketch变体。
a ^ i ≥ a a n d P r ( a ^ i > a i + ϵ ∥ a ⃗ ∥ ) ≤ 2 ϵ w 2 + ( 2 ϵ w ) d . \hat{a}_{i}\ge a\quad and\quad\mathbf{Pr}(\hat{a}_{i}>a_{i}+\epsilon\|\vec{a}\|)\le\frac{2}{\epsilon w^{2}}+\left(\frac{2}{\epsilon w}\right)^{d}. a^i≥aandPr(a^i>ai+ϵ∥a∥)≤ϵw22+(ϵw2)d.
特别是,对于 w ≥ 2 w\geq2 w≥2e / ϵ /\epsilon /ϵ 和 δ ≥ ln 1 / ϵ ( 1 − 1 / 2 e 2 ) \delta\geq\ln1/\epsilon(1-1/2\mathrm{e}^{2}) δ≥ln1/ϵ(1−1/2e2)
a ^ i ≥ a a n d P r ( a ^ i > a i + ϵ ∥ a ⃗ ∥ ) ≤ ϵ . \hat{a}_{i}\geq a\quad and\quad\mathbf{Pr}(\hat{a}_{i}>a_{i}+\epsilon\|\vec{a}\|)\leq\epsilon. a^i≥aandPr(a^i>ai+ϵ∥a∥)≤ϵ.
证明。修复一些项目 $i $ 。设 A i A_{i} Ai 是所有项目 Z(除了 i ˙ \dot{i} i˙ )的总数,其中 h 1 ( z ) = h 1 ( i ) h_{1}(z)=h_{1}(i) h1(z)=h1(i) 和 h 2 ( z ) = h 2 ( i ) h_{2}(z)=h_{2}(i) h2(z)=h2(i) 。设 B j , i B_{j,i} Bj,i 是 g j ( i ) = g j ( z ) g_{j}(i)=g_{j}(z) gj(i)=gj(z) 的所有项目 Z 的总数,不包括 i i i 和计入 A i A_{i} Ai 的项目 2。因此
a ^ i = min j = 0 d − 1 Count [ j , g j ( i ) ] = a i + A i + min j = 0 d − 1 B j , i . \hat{a}_i=\min\limits_{j=0}^{d-1}\text{Count}[j,g_j(i)]=a_i+A_i+\min\limits_{j=0}^{d-1}B_{j,i}. a^i=j=0mind−1Count[j,gj(i)]=ai+Ai+j=0mind−1Bj,i.
现在,下限紧跟在 allitems 具有非负计数的事实之后。因为所有更新都是积极的。因此,我们专注于上限,我们通过注意到
P
r
(
a
^
i
≥
a
i
+
ϵ
∥
a
⃗
∥
)
≤
P
r
(
A
i
≥
ϵ
∥
a
⃗
∥
/
2
)
+
P
r
(
min
j
=
0
d
−
1
B
j
,
i
≥
ϵ
∥
a
⃗
∥
/
2
)
.
\mathbf{Pr}(\hat a_i\ge a_i+\epsilon\|\vec a\|)\le\mathbf{Pr}(A_i\ge\epsilon\|\vec a\|/2)+\mathbf{Pr}\left(\min\limits_{j=0}^{d-1}B_{j,i}\ge\epsilon\|\vec a\|/2\right).
Pr(a^i≥ai+ϵ∥a∥)≤Pr(Ai≥ϵ∥a∥/2)+Pr(j=0mind−1Bj,i≥ϵ∥a∥/2).
我们首先绑定了
A
i
A_{i}
Ai 。设
1
(
⋅
)
1(\cdot)
1(⋅) 表示指标函数,我们有
E
[
A
i
]
=
∑
z
≠
i
a
z
E
[
1
(
h
1
(
z
)
=
h
1
(
i
)
∧
h
2
(
z
)
=
h
2
(
i
)
)
]
≤
∑
z
≠
i
a
z
/
w
2
≤
∥
a
⃗
∥
/
w
2
,
\mathbf{E}[A_i]=\sum\limits_{z\ne i}a_z\:\mathbf{E}[\mathbf{1}(h_1(z)=h_1(i)\wedge h_2(z)=h_2(i))]\le\sum\limits_{z\ne i}a_z/w^2\le\|\vec{a}\|/w^2,
E[Ai]=z=i∑azE[1(h1(z)=h1(i)∧h2(z)=h2(i))]≤z=i∑az/w2≤∥a∥/w2,
其中第一步来自期望的线性,第二步来自哈希函数的定义。马尔可夫不等式现在意味着
Pr
(
A
i
≥
ϵ
∥
a
⃗
∥
/
2
)
≤
2
/
ϵ
w
2
.
\Pr(A_{i}\geq\epsilon\|\vec{a}\|/2)\leq2/\epsilon w^{2}.
Pr(Ai≥ϵ∥a∥/2)≤2/ϵw2.
要绑定
min
j
=
0
d
−
1
B
j
,
i
\operatorname*{min}_{j=0}^{d-1}B_{j,i}
minj=0d−1Bj,i ,我们注意到对于任何
j
∈
{
0
,
…
,
d
−
1
}
j\in\{0,\ldots,d-1\}
j∈{0,…,d−1} 和
z
≠
i
z\neq i
z=i
P
r
(
(
(
h
1
(
z
)
≠
h
1
(
i
)
∨
h
2
(
z
)
≠
h
2
(
i
)
)
∧
g
j
(
z
)
=
g
j
(
i
)
)
≤
P
r
(
g
j
(
z
)
=
g
j
(
i
)
)
=
P
r
(
h
1
(
z
)
=
h
1
(
i
)
+
j
(
h
2
(
i
)
−
h
2
(
z
)
)
=
1
/
w
,
\begin{aligned}\mathbf{Pr}(((h_{1}(z)\neq h_{1}(i)\vee h_{2}(z)\neq h_{2}(i))\wedge g_{j}(z)=g_{j}(i))&\leq\mathbf{Pr}(g_{j}(z)=g_{j}(i))\\&=\mathbf{Pr}(h_{1}(z)=h_{1}(i)+j(h_{2}(i)-h_{2}(z))\\&=1/w,\end{aligned}
Pr(((h1(z)=h1(i)∨h2(z)=h2(i))∧gj(z)=gj(i))≤Pr(gj(z)=gj(i))=Pr(h1(z)=h1(i)+j(h2(i)−h2(z))=1/w,
所以
E
[
B
j
,
i
]
=
∑
z
≠
i
a
z
E
[
1
(
(
h
1
(
z
)
≠
h
1
(
i
)
∨
h
2
(
z
)
≠
h
2
(
i
)
)
)
∧
g
j
(
z
)
=
g
j
(
i
)
)
]
≤
∥
a
⃗
∥
/
w
,
\mathbf{E}[B_{j,i}]=\sum_{z\ne i}a_z\:\mathbf{E}[\mathbf{1}((h_1(z)\ne h_1(i)\vee h_2(z)\ne h_2(i)))\wedge g_j(z)=g_j(i))]\le\|\vec{a}\|/w,
E[Bj,i]=z=i∑azE[1((h1(z)=h1(i)∨h2(z)=h2(i)))∧gj(z)=gj(i))]≤∥a∥/w,
因此,马尔可夫不等式意味着
P
r
(
B
j
,
i
≥
ϵ
∥
a
⃗
∥
/
2
)
≤
2
/
ϵ
w
\mathbf{Pr}(B_{j,i}\geq\epsilon\|\vec{a}\|/2)\leq2/\epsilon w
Pr(Bj,i≥ϵ∥a∥/2)≤2/ϵw
对于任意
u
b
ub
ub ,这个结果不足以绑定
min
j
=
0
d
−
1
B
j
,
i
.
\operatorname*{min}_{j=0}^{d-1}B_{j,i}.
minj=0d−1Bj,i. 但是,由于
u
b
ub
ub 是素数,每个项目
Z
Z
Z 只能对一个
B
k
,
i
B_{k,i}
Bk,i 做出贡献(因为如果
g
j
(
z
)
=
g
j
(
i
)
g_{j}(z)=g_{j}(i)
gj(z)=gj(i) 对于两个
j
j
j 的值,我们必须有
h
1
(
z
)
=
h
1
(
i
)
h_{1}(z)=h_{1}(i)
h1(z)=h1(i) 和
h
2
(
z
)
=
h
2
(
i
)
h_{2}(z)=h_{2}(i)
h2(z)=h2(i) , 在这种情况下,2 的计数不包括在任何
B
j
,
i
B_{j,i}
Bj,i ) 中。从这个意义上说,
B
j
,
i
B_{j,i}
Bj,i 是负依赖性的 [7]。因此,对于任何 $U $ 的值
P
r
(
min
j
=
0
d
−
1
B
j
,
i
≥
v
)
≤
∏
j
=
0
d
−
1
P
r
(
B
j
,
i
≥
v
)
\mathbf{Pr}\left(\min\limits_{j=0}^{d-1}B_{j,i}\geq v\right)\leq\prod\limits_{j=0}^{d-1}\mathbf{Pr}(B_{j,i}\geq v)
Pr(j=0mind−1Bj,i≥v)≤j=0∏d−1Pr(Bj,i≥v)
特别是,我们有
P
r
(
min
j
=
0
d
−
1
B
j
,
i
≥
ϵ
∥
a
⃗
∥
/
2
)
≤
(
2
/
ϵ
w
)
d
,
\mathbf{Pr}\left(\min\limits_{j=0}^{d-1}B_{j,i}\geq\epsilon\|\vec{a}\|/2\right)\leq(2/\epsilon w)^d,
Pr(j=0mind−1Bj,i≥ϵ∥a∥/2)≤(2/ϵw)d,
所以
P
r
(
a
^
i
≥
a
i
+
ϵ
∥
a
⃗
∥
)
≤
P
r
(
A
i
≥
ϵ
∥
a
⃗
∥
/
2
)
+
P
r
(
min
j
=
0
B
j
,
i
≥
ϵ
∥
a
⃗
∥
/
2
)
≤
2
ϵ
w
2
+
(
2
ϵ
w
)
d
.
\begin{aligned}\mathbf{Pr}(\hat{a}_{i}\geq a_{i}+\epsilon\|\vec{a}\|)&\leq\mathbf{Pr}(A_{i}\geq\epsilon\|\vec{a}\|/2)+\mathbf{Pr}\left(\operatorname*{min}_{j=0}B_{j},i\geq\epsilon\|\vec{a}\|/2\right)\\&\leq\frac{2}{\epsilon w^{2}}+\left(\frac{2}{\epsilon w}\right)^{d}.\end{aligned}
Pr(a^i≥ai+ϵ∥a∥)≤Pr(Ai≥ϵ∥a∥/2)+Pr(j=0minBj,i≥ϵ∥a∥/2)≤ϵw22+(ϵw2)d.
对于
w
≥
2
w\geq2
w≥2e
/
ϵ
/\epsilon
/ϵ 和
δ
≥
ln
1
/
ϵ
(
1
−
1
/
2
e
2
)
\delta\geq\ln1/\epsilon(1-1/2\mathrm{e}^{2})
δ≥ln1/ϵ(1−1/2e2) ,我们有
2
ϵ
w
2
+
(
2
ϵ
w
)
d
≤
ϵ
/
2
e
2
+
ϵ
(
1
−
1
/
2
e
2
)
=
ϵ
,
\begin{aligned}\frac{2}{\epsilon w^2}+\left(\frac{2}{\epsilon w}\right)^d\leq\epsilon/2e^2+\epsilon(1-1/2\text{e}^2)=\epsilon,\end{aligned}
ϵw22+(ϵw2)d≤ϵ/2e2+ϵ(1−1/2e2)=ϵ,
完成证明
10.结论
布隆过滤器是简单的随机数据结构,在实践中非常有用。事实上,它们非常有用,以至于执行 Bloom 过滤器操作所需的时间的任何显著减少都会立即转化为许多实际应用程序的大幅加速。不幸的是,Bloom 过滤器非常简单,以至于它们没有留下太多的优化空间。本文重点介绍如何修改 Bloom 过滤器以减少它们唯一依赖的资源 -
tionally use liberally: (伪)随机性。由于唯一由 .布隆过滤器是伪随机哈希函数的构造和评估,伪随机哈希函数所需数量的任何减少都会使执行布隆过滤器操作所需的时间减少几乎相等(当然,假设布隆过滤器完全存储在内存中,因此可以非常快速地执行随机访问)我们已经证明,布隆过滤器可以只用两个伪随机哈希来实现
函数时,渐近假阳性概率没有任何增加,并且,对于具有合理参数的固定大小的 Bloom 滤波器,假阳性概率没有任何实质性增加。我们还表明,渐近假阳性概率在所有实际目的和布隆滤波器参数的合理设置中起作用,就像假阳性率一样。这个结果具有巨大的实际意义,因为标准 Bloom 滤波器的类似结果本质上是它们广泛使用的理论理由。更一般地说,我们给出了一个分析修改后的 Bloom 过滤器的通用框架,该框架
我们预计将来将用于改进我们在本文中分析的具体方案。我们还希望本文中使用的技术能够有效地应用于其他数据结构,正如我们对 Count-Min Sketch的修改所证明的那样。
致谢
我们非常感谢 Peter Dillinger 和 Panagiotis Manolios 向我们介绍了这个问题,为我们提供了他们工作的提前副本,并提供了许多有用的讨论。
引用
[1] P. Billingsley. Probability and Measure, Third Edition. John Wiley & Sons, 1995.
[2] P. Bose, H. Guo, E. Kranakis, A. Maheshwari, P. Morin, J. Morrison, M. Smid, and Y Tang. On the false-positive rate of Bloom filters. Submitted. Temporary version available at http://cg.scs.carleton.ca/~morin/publications/ds/bloom-submitted.pdf [3]A. Broder and M. Mitzenmacher. Network Applications of Bloom Filters: A Survey. Internet Mathematics, to appear. Temporary version available at http: //www.eecs.harvard. edu/. ~michaelm/postscripts/tempim3.pdf [4] G. Cormode and S. Muthukrishnan. Improved Data Stream Summaries: The Count-Min Sketch and its Applications. DIMACS Technical Report 2003-20, 2003 [5]P. C. Dillinger and P. Manolios. Bloom Filters in Probabilistic Verification. FMCAD 2004, Formal Methods in Computer-Aided Design, 2004. [6]P. C. Dillinger and P. Manolios. Fast and Accurate Bitstate Verification for SPIN. SPIN 2004, 11th International SPIN Workshop on Model Checking of Software, 2004.
[7]D. P. Dubhashi and D. Ranjan. Balls and Bins: A Case Study in Negative Dependence. Random Structures and Algorithms, 13(2):99-124, 1998 [8]L.Fan, P. Cao, J. Almeida,and A. Z. Broder. Summary cache: a scalable wide-area Web cache sharing protocol. IEEE/ACM Transactions on Networking, 8(3):281-293, 2000 [9] K. Ireland and M. Rosen. A Classical Introduction to Modern Number Theory, Second Edition. Springer-Verlag, New York, 1990 [10]D. Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching. AddisonWesley, Reading Massachusetts, 1973. [11] M. Mitzenmacher. Compressed Bloom Filters. IEEE/ACM Transactions on Networking. 105:613-620, 2002 [12] M. Mitzenmacher and E. Upfal. Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press, 2005. [13] M. V. Ramakrishna. Practical performance of Bloom filters and parallel free-text searching Communications of the ACM, 32(10):1237-1239, 1989.
























 459
459

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








