数据结构学习笔记＜6＞ 堆与哈夫曼树与并查集

一、堆

1.堆是什么

堆（Heap),是一个可以被看做一棵完全二叉树的数组对象，有以下性质：

• 任意节点的值是其子树所有结点中的最大值/最小值（有序性）
• 堆总是一棵用数组表示的完全二叉树。
  

2.最大堆的操作函数

定义

typedef struct HeapStruct *MaxHeap;
struct HeapStruct {
	ElementType *Elements;//存储堆元素的数组
	int Size;//当前元素个数
	int Capacity;//最大容量
};

(1)空最大堆的创建(Create函数)

MaxHeap Create(int MaxSize) {
	MaxHeap H = malloc(sizeof(struct HeapStruct) );
	H->Elements = malloc( (MaxSize+1) * sizeof(ElementType));//+1是由于我们从下标1开始存储
	H->Size = 0;
	H->Capacity = MaxSize;
	H->Elements[0] = MaxData;//下标0设为"哨兵" 为大于堆中所有可能元素的值，便于之后的操作
	return H;
}

(2)最大堆的插入(Insert函数)

插入一个元素时与其父结点比较，若插入元素更大则两者交换，再与其父节点比较，如此直到插入元素比父结点小为止。

void Insert(MaxHeap H, ElementType item) {
	int i;
	if(IsFull(H)) {
		printf("最大堆已满");
		return;
	}
	i = ++H->Size;//i指向插入后队中最后一个元素的位置。
	for(; H->Elements[i/2] < item; i /= 2) {//当item的父结点的值小于item值循环才继续
		H->Elements[i] = H->Elements[i/2];//向下过滤结点（）
	}
	H->Elements[i] = item;//将item插入
}

(3)最大堆的删除(Delete函数)

取出根节点（最大值）元素，同时在堆中删除根结点，保证其新的根节点仍是堆中的最大值。

• 用最大堆中最后一个元素，作为新的根节点，删除原来的最后一个元素
• 看根结点左右儿子是否比其大，是则继续往下过滤

ElementType DeleteMax(MaxHeap H) {
	int Parent,Child;//父结点，孩子结点
	ElementType MaxItem, temp;
	if(IsEmpty(H) ) {
		printf("最大堆已空");
		return;
	}
	MaxItem = H->Elements[1]; //取出根结点最大值，暂存在MaxItem中
	temp = H->Elements[H->Size--];//存储最后一个元素，然后size--
	for (Parent = 1; Parent*2 <= H->Size; Parent = Child) {
		Child = Parent * 2;//Child此时为Parent的左孩子
		if (Child != H->Size && H->Elements[Child] < H->Elements[Child+1] ) {
			Child++;	//当且仅当右孩子存在且其值比左孩子大时，Child变成右孩子的下标
		} 
		if (temp >= H->Elements[Child] ) break;//temp找到了应该放的地方
		else //用孩子结点的值取代父结点
			H->Elements[Parent] = H->Elements[Child];
	}
	H->Elements[Parent] = temp;
	return MaxItem;//返回删除前最大值
}

(3)从已有元素创建最大堆

将已经存在的N个元素按最大堆的要求存放在一个一维数组中。

• 法1 通过插入操作，将N个元素一个个插入到一个空的最大堆中，时间复杂度最大为O(NlogN)。
• 法2 在线性时间复杂度下建立最大堆。
• （1）将N个元素按输入顺序存入，使其先满足完全二叉树的结构特性
• （2）调整各结点位置，使其满足最大堆的有序特性

建堆时间复杂度O(n)，为书中各结点的高度和
从倒数第一个有儿子的结点开始，其肯定有左儿子
将定义中的Elements数组改成Data数组存储已有元素

void PercDown(MaxHeap H, int p) {//将H中以H->Data[p]为根的子堆调整为最大堆 原理同删除操作
	int Parent,Child;
	ElementType X;
	X = H->Data[p];//取出根结点值
	for(Parent = p; Parent*2 <= H->Size; Parent = Child) {
		Child = Parent * 2;
		if( Child != H->Size && H->Data[Child] < H->Data[Child+1]) {
			Child++;
		}
		if(X >= H->Data[Child]) break;//找到了合适位置
		else 
			H->Data[Parent] = H->Data[Child];
	}
	H->Data[Parent] = X;
}
void BuildHeap(MaxHeap H) {//调整H->Data[]中的元素使其满足最大堆的有序性，此处假设所有H->Size个元素都已存在H->Data[]中
	int i;
	//从最后一个结点的父节点开始，到根结点1
	for(i = H->Size/2; i > 0; i--)
		PercDown(H,i);
}

二、哈夫曼树

1.哈夫曼树是什么

带权路径长度(WPL)：设二叉树有n个叶子结点，每个叶子结点带有权值w_k，从根结点到每个叶子结点的长度为l_k，则每个叶子结点的带权路径长度之和就是：WPL = ${\sum }_{k=1}^n$w_k l_k.
最优二叉树，也称为哈夫曼树(Huffman Tree):WPL最小的二叉树，其特点为：

• 没有度为1的结点
• n个叶子结点的哈夫曼树共有2n-1个结点
• 哈夫曼树的任意非叶结点的左右子树交换后仍是哈夫曼树
• 同一组权值，是可能存在不同构的两棵哈夫曼树的
  

2.哈夫曼树的操作

哈夫曼树的构造，每次将权值最小的两棵二叉树合并
主要问题：如何选取两个最小的？利用最小堆！

typedef struct TreeNode *HuffmanTree;
struct TreeNode {
	int Weight;
	HuffmanTree Left,Right;
};
HuffmanTree Huffman(MinHeap H) {
	//假设H->Size个权值已经存在了H->Elements[]->Wight里
	int i;	HuffmanTree T;
	BuildMinHeap(H);//将H->Elements[]按权值调整为最小堆
	for(i = 1; i < H->Size; i++) {//做H->Size-1次合并
		T = malloc(sizeof(struct TreeNode));//建立新结点
		T->Left = DeleteMin(H);//从最小堆中删除一个结点，作为新T的左子结点
		T->Right = DeleteMin(H);//从最小堆中删除一个结点，作为新T的右子结点
		T->Weight = T->Left->Weight + T->Right->Weight;
		Insert(H,T);//将新T插入最小堆
	}
	T = DeleteMin(H);
	return T;
}

3.哈夫曼树的应用——哈夫曼编码

如何进行编码，可以使总编码空间最少？
出现频率高的字符用的编码短些，出现频率低的字符编码可以长一些，同时要避免二义性。
前缀码(prefix code)： 任何字符的编码都不是另一字符的前缀，即可避免二义性
可以构造一个二叉树用于编码，左右分支分别为0、1，当所有的字符都在叶结点上的时候即可

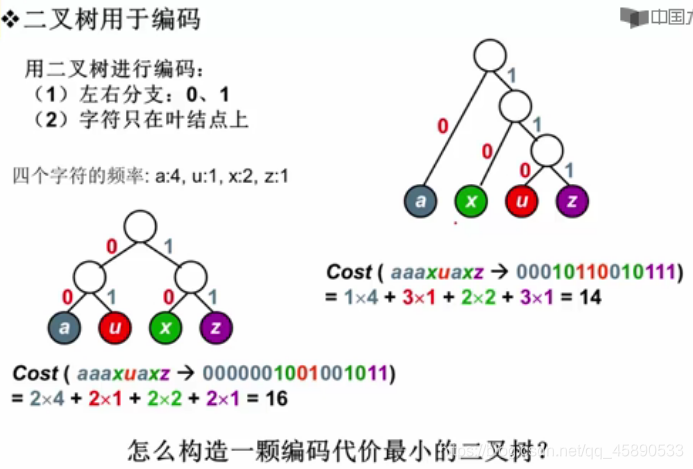
就可以用哈夫曼树！

三、集合

关于集合这一块主要就是并查集，之前有学过这篇博客写的超棒：超有爱的并查集~(原博挂了，转载)
所以在这儿就不多说啦~

~ 并查集板子 ~

#include <iostream>
#include <set>
using namespace std;
const int maxn = 1000000;
int fa[maxn];
int ans[maxn];
void init(int n) {
    for (int i = 1; i <= n; i++) {
        fa[i] = i;
    }
}
int find(int x) {//查询+路径压缩 找根节点并将沿途每个结点的父节点都设为根节点
    return x == fa[x]? x : (fa[x] = find(fa[x]));
}
inline void merge(int a, int b) {
    fa[find(a)] = find(b);
}
int main() {
    int m, n, k, x;
    cin >> m >> n >> k;
    x = n*m;
    init(x);
    for (int i = 0; i < k; i++) {
        int a,b;
        cin >> a >> b;
        merge(a, b);
    }
    for(int i = 1; i <= x; i++) {
        ans[find(i)] = 1;
    }
    int cnt = 0;
    for (int i = 1; i <= x; i++) {
        if(ans[i] == 1) cnt++;
    }
    cout << cnt << endl;
    return 0;
}