本部分视频所在地址:深度强化学习的理论与实践
2.1节 动态规划简介
态规划有两种思路:分治法和动态规划,目的是求解一个大问题。
分治法
分治法是将一个大问题分解成多个相互独立的子问题。然后再逐个解决每个子问题,最后将多个问题的计算结果c1、c2、…、cn进行总结,最后得到总问题的解。
subp1:表示将大问题分成的子问题
这些子问题的特点是这些子问题之间是相互独立的,也就是这些子问题是可以独立求解的。
动态规划
这个方法是将一个总问题进行逐步求解,先求解subp1,再求解subp2,…,最后求解subpn问题,
子问题的特点是嵌套的,递归的求解,即想要解决子问题subp3,必须先要求解子问题subp2,想要解决子问题subp2,必须先要求解子问题subp1。每个子问题的结构是一样的,即如果一个子问题是加法问题,则所有问题都是加法问题。

找到的其结构特征,就是去找到嵌套的结构特征

动态规划解决问题的案例

2.2节 值函数与贝尔曼方程
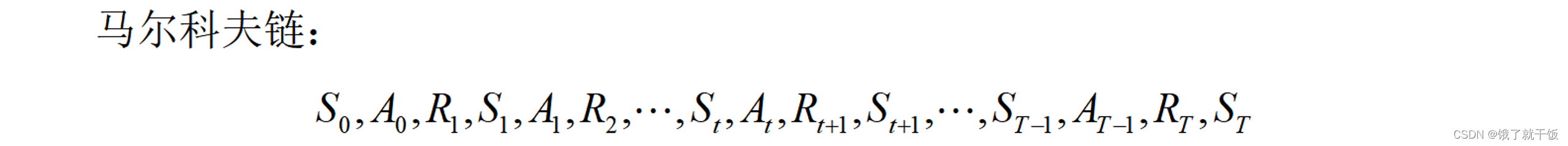
根据马尔科夫链定义一些东西:
即时奖励(通常称为奖励,reward)
累计奖励Gt: 表示状态为St时执行动作At之后累积的奖励。累计奖励中每一个时刻对应的即时奖励不能够同等看待。原因是例如在下象棋时第一步走马和棋局最后几步走马同样是走马的动作,但是走马的动作重要性是不同的。所得到的即时奖励是不同的。在棋局最后的终止状态附近的奖励应该被认为是更重要的。
累积折扣奖励(通常称回报,return): 智能体在t时刻的累积奖励会这么认为,离该时刻越近的即时奖励重要性应该越大,离该时刻越远的即时奖励重要性越小。举例:在终止状态T时刻,RT的重要性要远超于R1的重要性,其根本原因是动作AT-1的重要性要远超于动作A0的重要性。
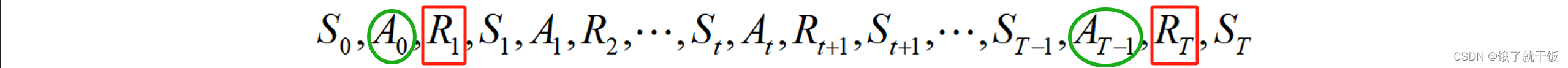
延时越长时RT,对Gt的影响越小: 延时越长时RT,即T越大,参数γ经过T指数后参数变得很小,因此对Gt的影响越小。
强化学习的目的或目标: 寻找到一个能够使累积折扣奖励Gt最大的最优策略。如果该策略可以使得每一个时刻的累积折扣奖励都最大,这个策略是最优的。

有了累积折扣奖励函数之后,进一步定义两个值函数:状态值函数、动作值函数。

上面的Rt+1应该写成Rt+k

从上面的式子可以看出来,对于每个状态和每一个动作都会对应一个动作值,对于离散的状态空间和动作空间来讲那么动作值的个数应该是有限的,此时将会使用一个表来表示这个Q,之后会学习一种基于表的强化学习方法。
‘状态值函数和动作值函数之间是可以相互转换的。’

上面是假设s的下一个状态为s'
详细解释与推导:

动态规划的核心:贝尔曼方程。下面的两个方程认真一点都能写出来,需要注意的是在
1)状态值函数表达的贝尔曼方程中的r是在s状态下执行动作a之后得到的奖励r,在得到的这个方程的时候是这么简写的。
2)写动作值函数的贝尔曼方程时第2个Q函数中的s和a都是下一时刻的状态和下一时刻的动作。因此动作值函数表达的贝尔曼方程中有4个变量:当前时刻状态s,当前时刻的动作a,下一时刻的状态s',下一时刻的动作a',比较复杂,而状态值函数表达的贝尔曼方程中只有2个变量:当前状态s和下一时刻状态s',形式较为简单。因此实际中使用状态值函数更多。
3)两种贝尔曼方程中的r是基于三元函数的。即r=r(s,a,s'),之前我们还定义过R=R(s,a),此处不是二元的。为什么是3元呢?:因为在方程里面求和的时候,求和符号下面的变量已知了,就代表下一时刻s’已经知道了,那r就采用三元的定义形式了。不过也可以写成二元的奖励函数,因此有了下面的基于二元奖励函数的贝尔曼方程。
4)三元价值函数和二元值函数的关系
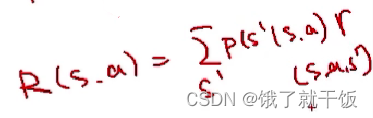



贝尔曼方程与动态规划的关系:贝尔曼是动态规划的发明人,s状态下的状态值函数可以使用下一时刻状态s’的状态值函数表示出来,也是动态规划的原理。
2.3节 策略评估
智能体思考在当前环境下要做出什么动作的过程就叫策略。

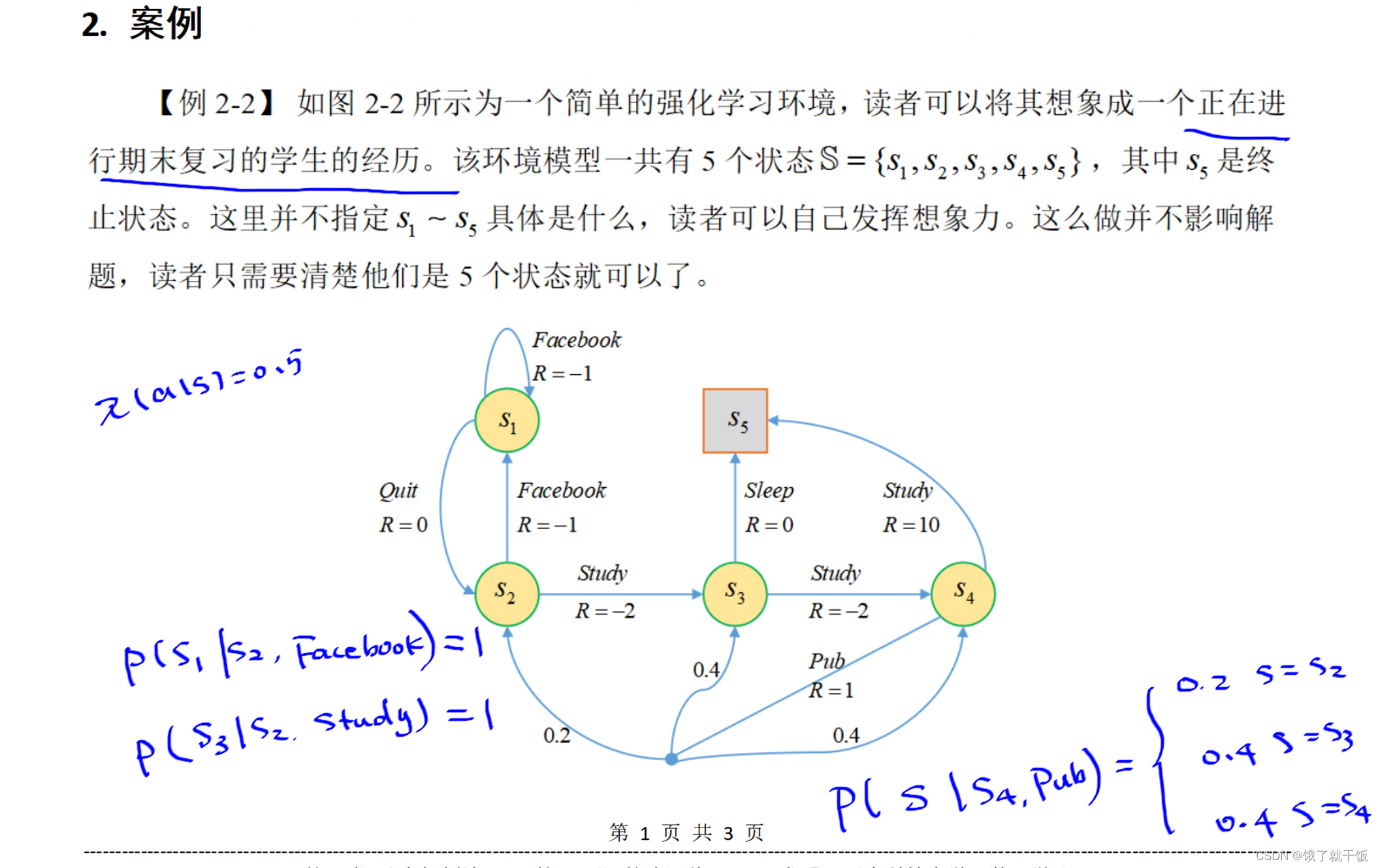
所有的终止状态的状态值函数都是0
下图中的状态转移概率在上图中已经展示了一部分,比较好写。使用的策略是平均策略,也即时在不管在哪个状态下,采取任意一个动作的概率均为0.5,也因为是每个状态下可采取的动作只有两个,定义策略时采用平均策略较好。

下图中基于状态值函数的贝尔曼方程中的4个方程就严格按照方程写是比较好写出来的。解出来的结果见下图

在V4的时候稍微麻烦一点,部分计算如下图
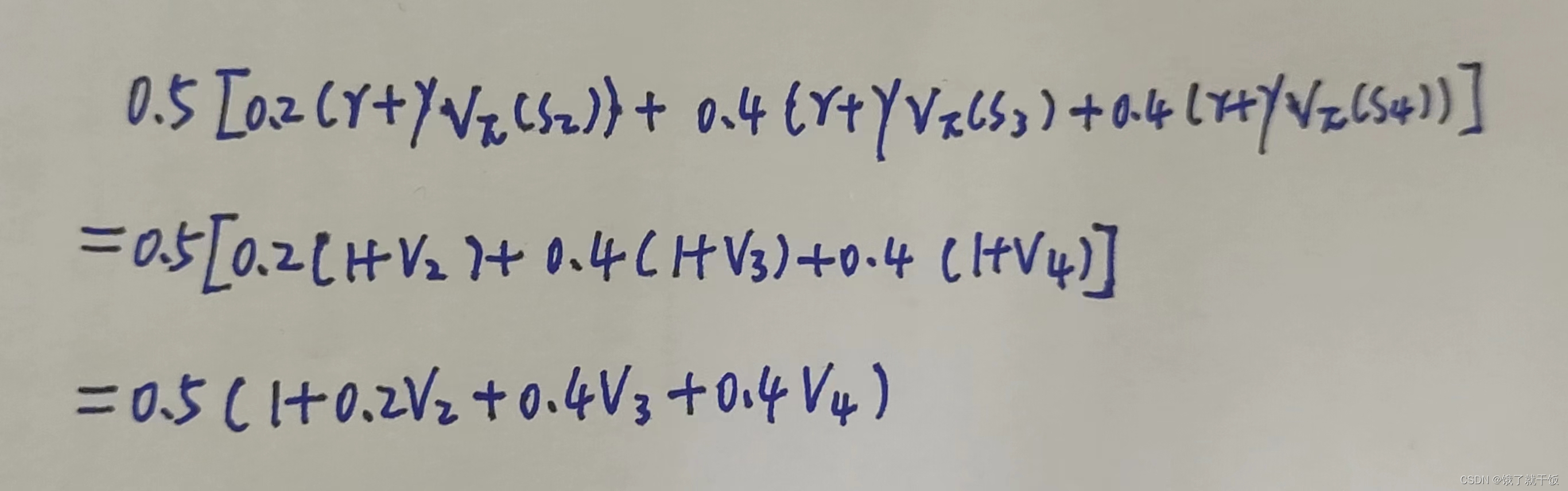
需要注意的一点:
联立的这个4元方程组一定是有解的,原因是:显然可以看出第1个方程中V2可以使用V1表示,第2个方程中V3可以使用V2表示,第3个方程中V4可以使用V3表示,而第4个方程中可以将所有变量均使用V1去表示,因此这个方程组可以合并成一个关于V1的方程,则必有解。我认为其他的场景下使用动态规划模型建模的强化学习方法使用方程组法去解则其解也类似如此唯一。
如果在秩的角度来解释:每个方程都是根据在不同状态下写出来的,每个状态是独立的,因此这几个方程是独立的,是不相关的,因此方程组的秩是满秩的,因此有唯一解。
当方程组很大的时候采用高斯消元法已经不够用了,此时使用迭代法来求解一个方程组。即先设置一个初值,经过贝尔曼方程的逐次计算得到一个迭代序列,经过多次迭代就会得到一个最终的近似解。迭代法之后用的更多,优点是速度快、方法简单,缺点是得到的解是近似解,不是精确解。

假如有一个新的策略π’,根据这个策略算出来一系列的状态值,这些状态值都要大于原来的策略π算出来的状态值,那么这个新策略π’就要比原来的策略π要好。具体为什么是这样,暂时不太清楚,存疑后解。

2.4节 策略改进
根据下面的定义可以得出结论:找最优的策略的就是去找最大的状态值函数。

π’(s)表示根据π’策略从状态s开始下一步执行的动作
策略改进定理:

证明:

上面证明的一个说明:在V的时候,下标是π或π’似乎无关紧要,不用纠结,当然认真抠细节的话,我觉着应该是薛定谔的V。

说明:策略改进定理是策略得到改进的充分条件,满足(2-14)的最简单的策略就是贪婪策略,贪婪策略简单解释为:在状态s时选择使得动作值函数最大的动作作为策略。
贪心策略一定是满足策略改进定理中的(2-14)式的。下图红色的公式是用动作值函数来表示状态值函数的公式。从该公式中可以看出,状态值函数是动作值函数的期望值,而π’(s)如果是选择在状态s时使得动作值函数最大的动作,那么Qπ(s,π’(s))则是最大的动作值函数,必大于等于动作值函数的期望值,也即是必大于等于状态值函数,因此满足(2-14)式,故该策略可有效改进。
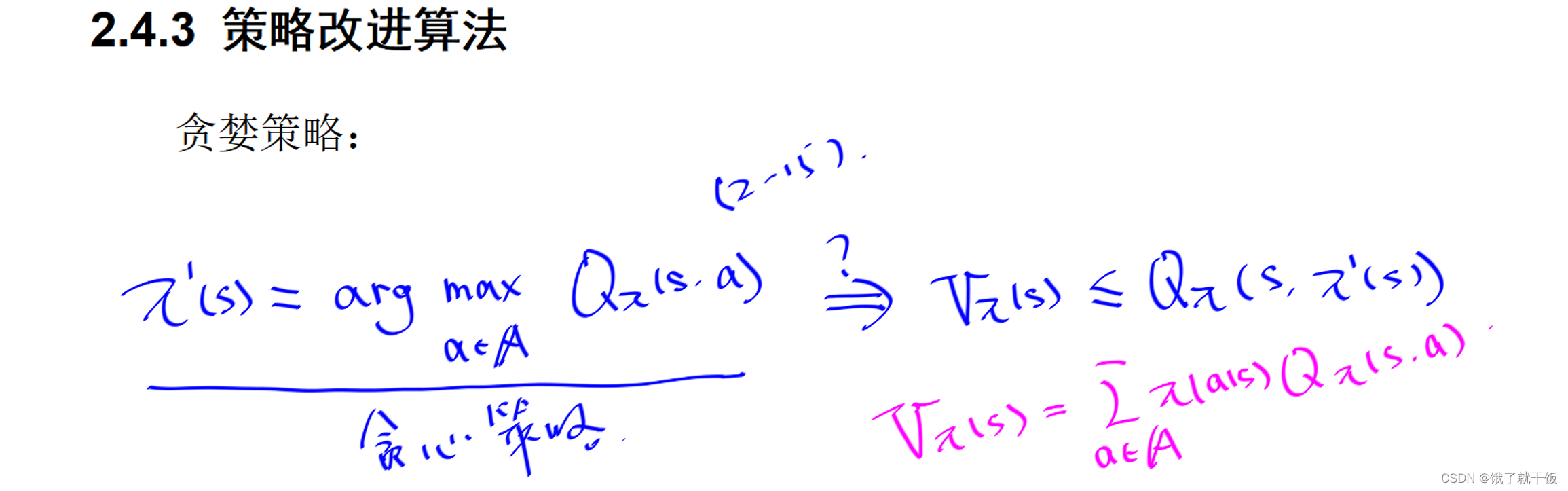
由下图Qπ(s,a)的表达公式,如果已知Vπ(s’)要去计算Qπ(s,a)需要知道状态转移函数p(s’|s,a),如果不知道状态转移函数p(s’|s,a)怎么办?可以使用基于动作值函数的贝尔曼方程去求解

基于动作值的贝尔曼方程见下图:(具体如何根据下图求解状态转移概率有待研究)


下面示例中的被划掉的0其实不应该写的。



2.5节 最优值函数与最优策略
本节讲最优策略与值函数之间的关系,首先定义两个最优值函数:最优状态值函数、最优动作值函数。

针对最优值函数公式的解释:假如有两个策略:平均策略和贪婪策略,针对特定状态,在这两个策略中能使得在该策略下使得状态值函数最大的策略就是该状态对应的最优的策略,对于任意的状态来说,挑选对应的最优策略,形成的最优状态值函数就是最优状态值函数。
最优动作值函数的解释和上面的解释类似。

性质有3(暂时不证明,证明很麻烦):
1)结论1解决了最优策略的存在性问题
2)最优策略下的状态值函数就是最优状态值函数
3)最优策略下的动作值函数就是最优动作值函数
根据3个性质可知假如我们找到了最优策略,那么通过计算在最优策略下的每一个状态值函数,就可以得到最优状态值函数,动作值函数也类似。假如我们计算出了最优状态值和最优动作值,那么最优状态值和最优动作值对应的策略就是最优策略。

如果π是最优策略则一定会满足上面红色框中的式子。即π是最优策略是该式子成立的充分条件。
基于状态值函数的贝尔曼最优方程与基于状态值函数的贝尔曼方程的区别在于最优值函数是基于状态值函数的贝尔曼方程的最大值,且使用的策略是最优策略。

下图的式子可能对下面的推导有用

下面的式子的推导不懂,先放着

如果π是最优策略则一定会满足上面红色框中的式子。即π是最优策略是该式子成立的充分条件。

方案1:
现有一个策略π,针对该策略进行评估,然后根据贪婪策略改进到一个贪婪策略π',针对该策略π’进行评估,然后根据贪婪策略改进到一个贪婪策略π’',如此下去策略序列收敛到π*。
方案2:由本节所讲的两个最优策略所应满足的条件:基于状态值函数的贝尔曼方程和基于动作值函数的贝尔曼方程来联立方程组进行求解,这个方程组和之前的贝尔曼方程组之间的区别在于它不是一个线性方程组,原因在于这两个方程中都含有max函数,不是线性方程组因此不可以使用高斯消元法来进行求解。可以使用迭代法求解该方程组即可得到最优策略。
2.6节 值迭代与策略迭代
策略评估:Policy Evalution(PE)
策略改进:Policy Improvement(PI)
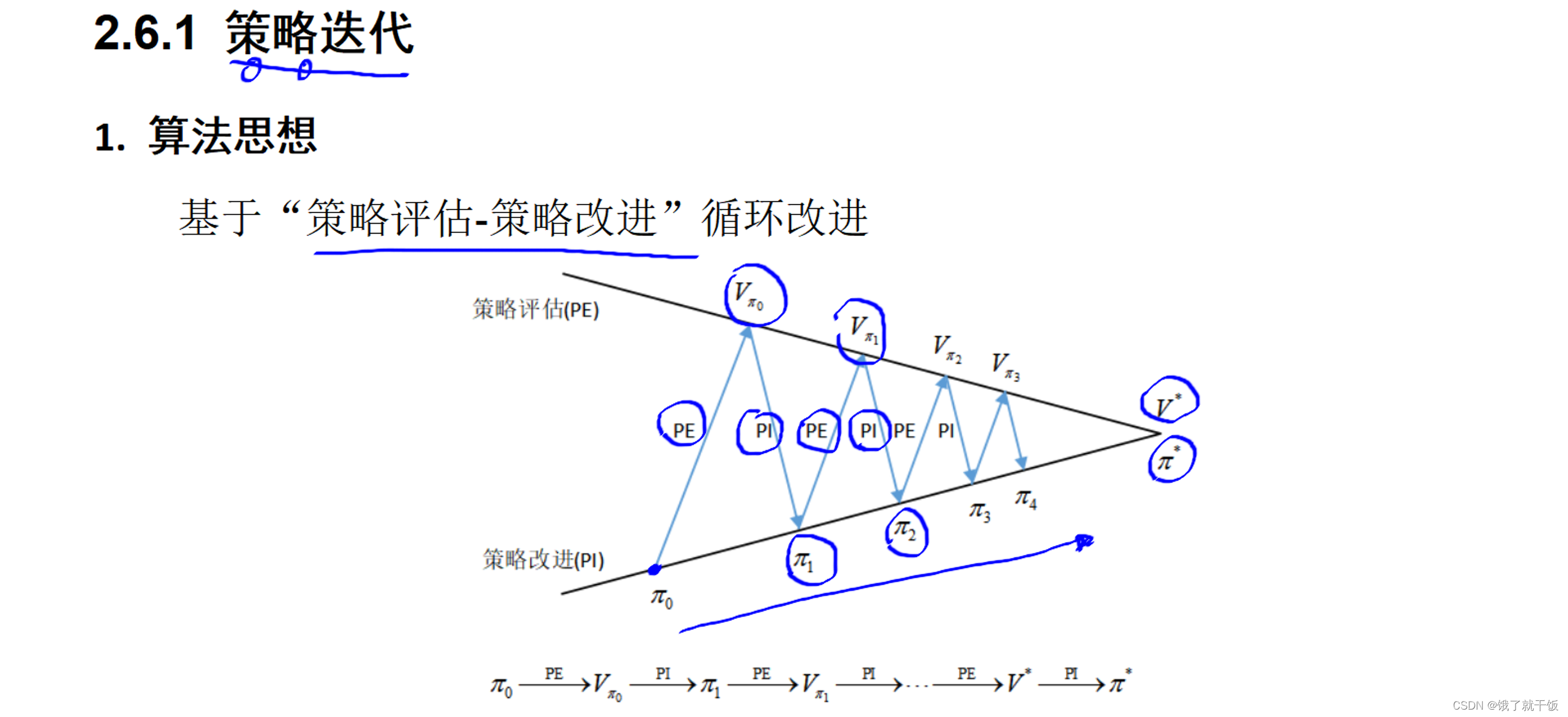
算法2-2是策略改进算法


上图的解释:
1)上面介绍了两种最优值函数的方程,因此可以使用两种迭代方法去求解最优策略,绿色的是一种方案,红色的是一种方案
2)流程:不管使用哪种方先迭代得到最优的值函数(包括状态值函数或动作值函数),箭头指向的是流程。
3)基于状态值函数:先迭代求出最优状态值函数V*,然后通过Q*(s,a)的表达式,然后算出Q*,通过计算argmax来找到最优的策略π*(s)
4)基于动作值函数:通过迭代公式多次迭代得到最优的Q,通过计算argmax来找到最优的策略π*(s)
5)红色的圈是表示不管使用哪种迭代方法都得使用状态转移概率
说明:
1)假设有4个状态,对应的状态也有4个,k表示步数,同步更新与异步更新发生在k=1到k=2的过程。
2)默认4个状态之间是可以相互转换的。下图中举的例子是k=2时,s1可能的转换例如s1—>s2和s1—>s4,那么第1种转换需要使用v2,第2种转换需要使用v4,此时s1的v1更新使用的是k=1时刻即使用上一时刻旧的状态值,这种更新称为同步更新。重新定义:在计算k=2时刻的所有状态值时全部使用的旧的状态值,这种更新方法是同步更新。
若在更新k=2时刻的v2时,使用的是已经更新好的v1,这种更新方法称为异步更新。
3)v2——>v1蓝色是同步更新,v1——>v2绿色是异步更新
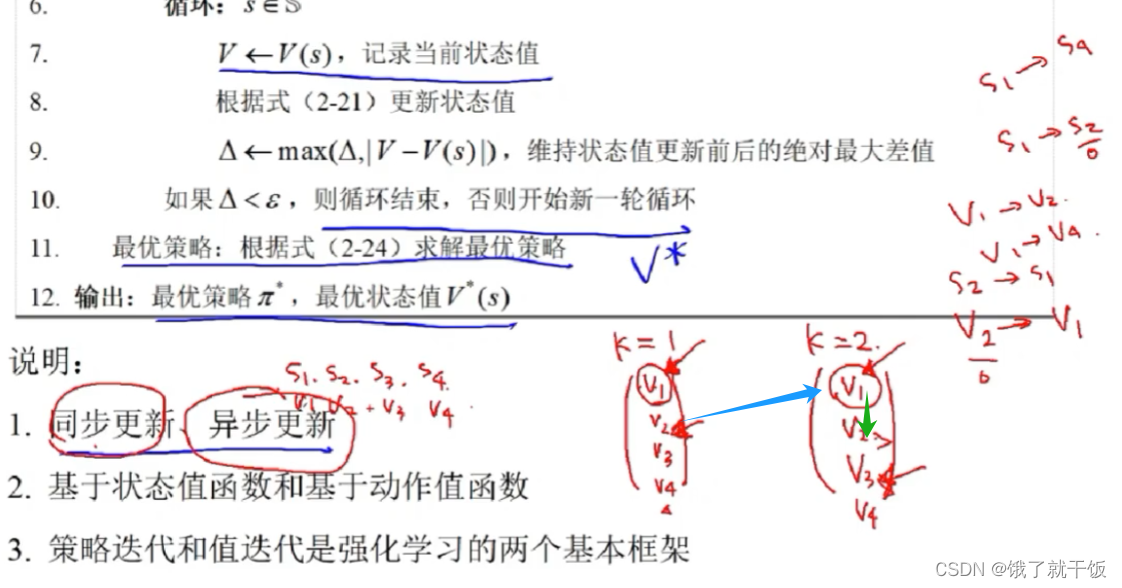
4)平时用的最多的是用状态值函数。

2.7节 动态规划求解最优策略
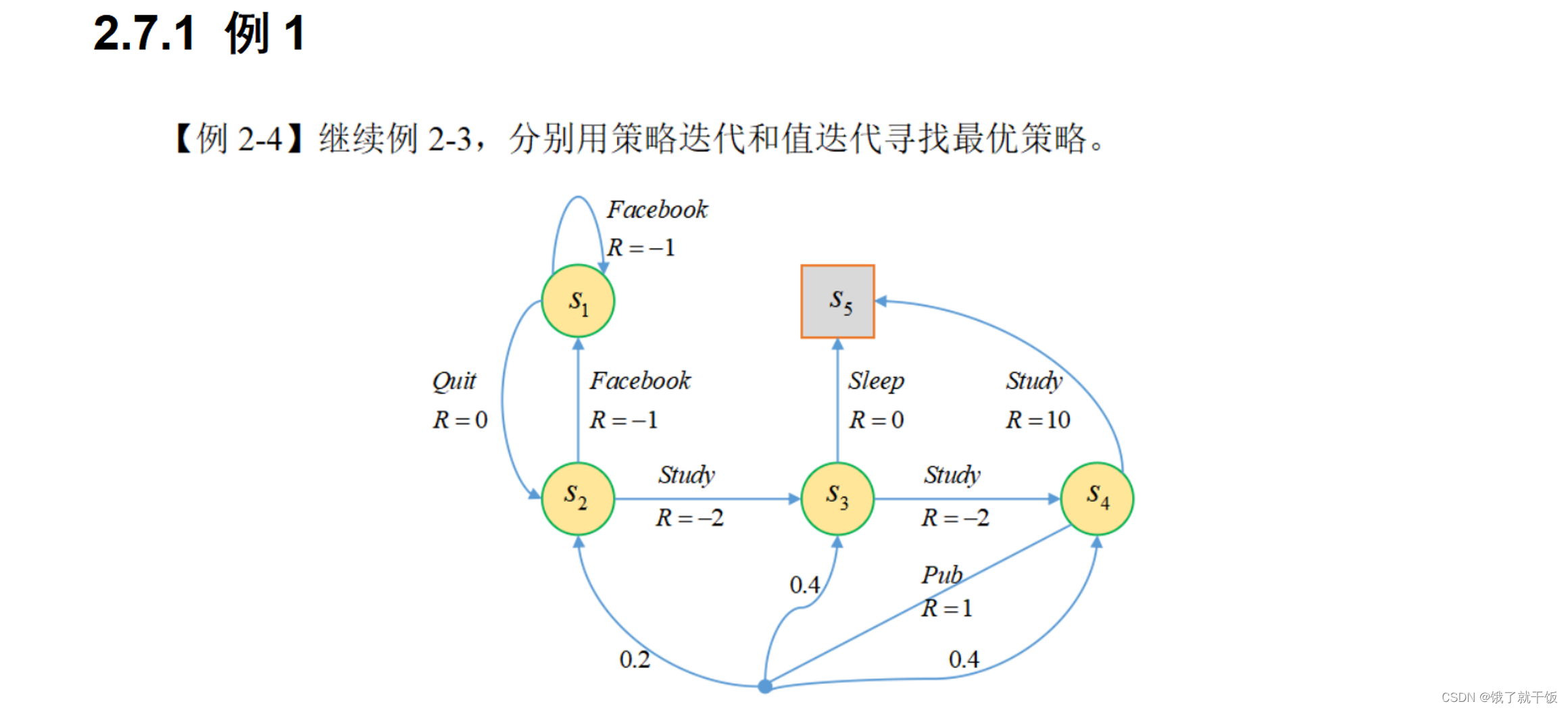


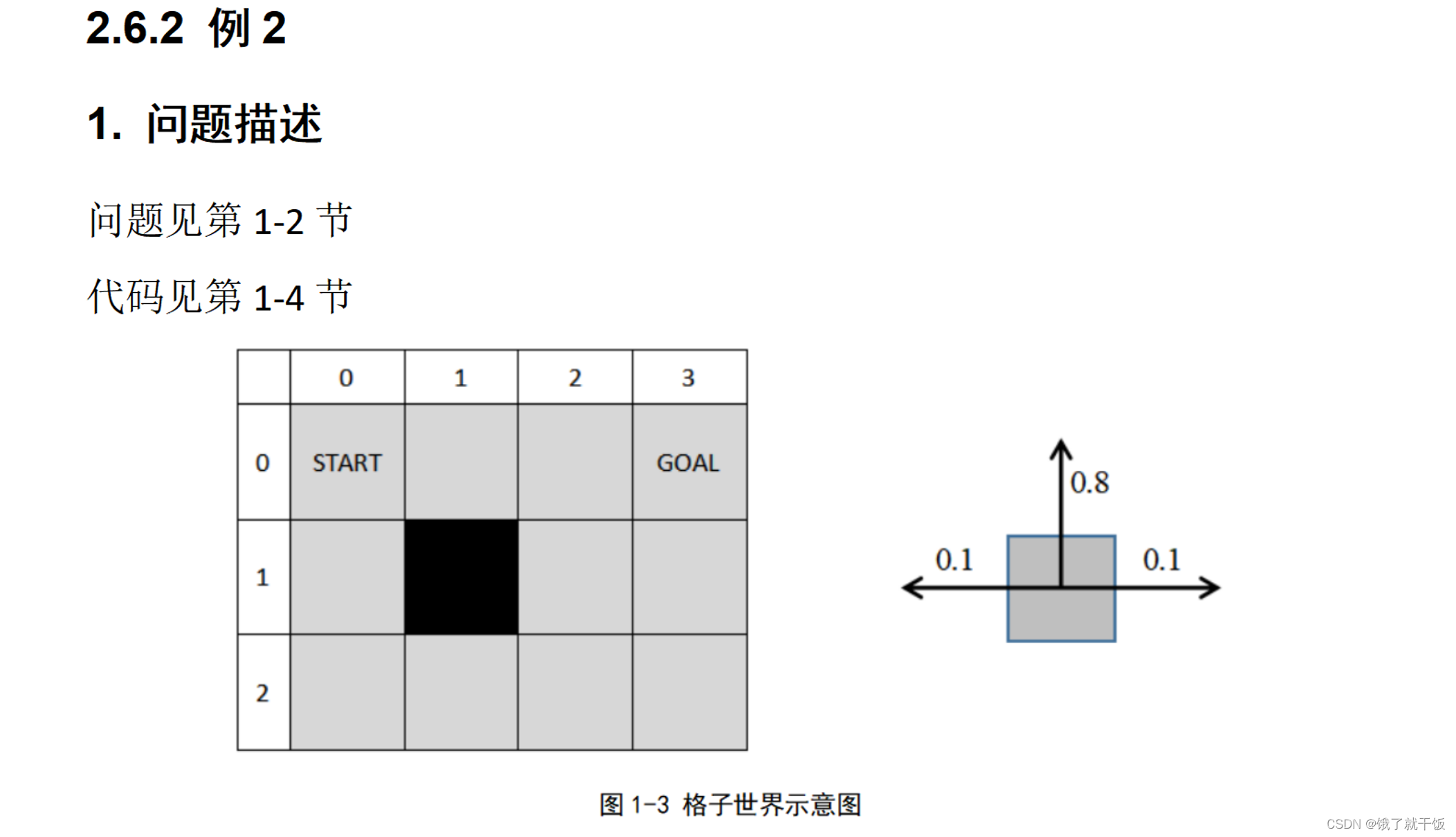
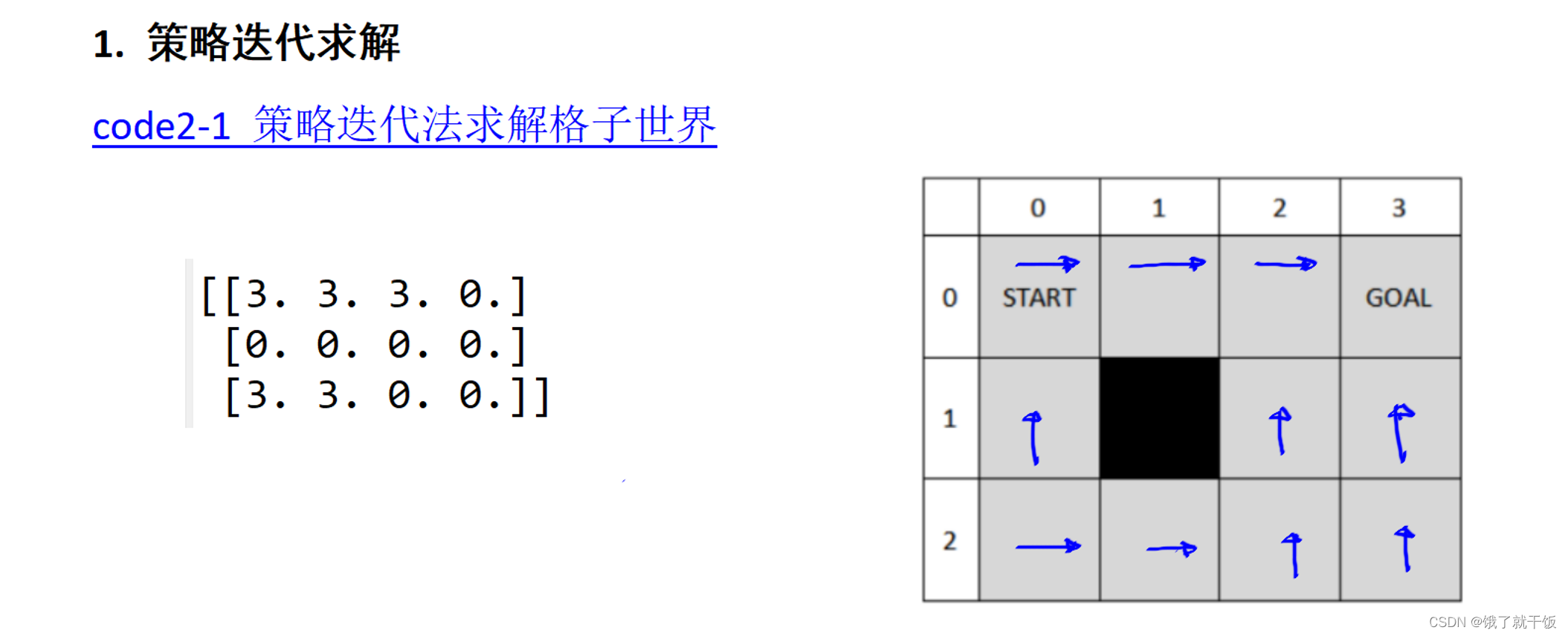
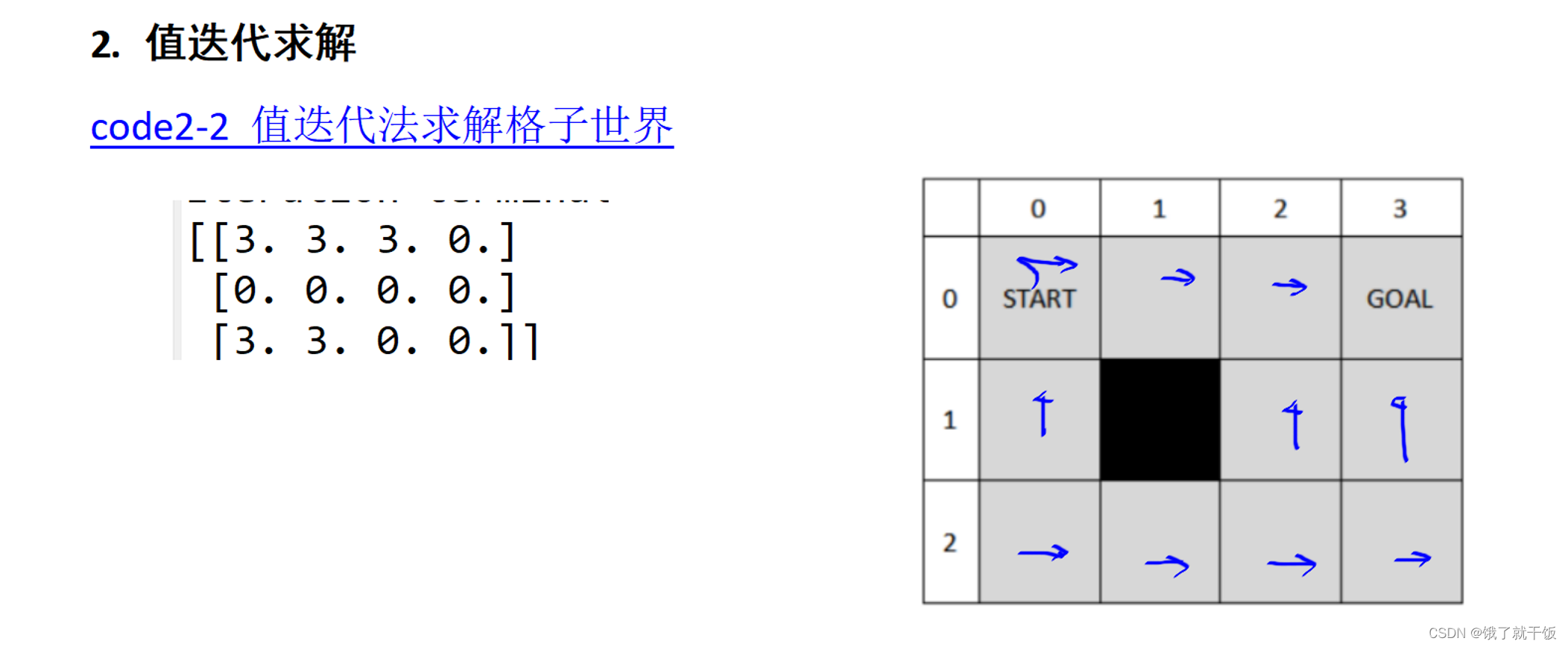























 598
598











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










