Ansys Workbench拓扑优化教程

已于 2023-12-27 18:59:56 修改
阅读量2.2w 收藏 121
点赞数 31
文章标签： 拓扑学 几何学 算法
于 2022-05-18 13:24:03 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_45895217/article/details/124840000
版权
本文介绍了拓扑优化在结构设计中的应用，通过赵州桥的例子展示了其简化结构和节省材料的优势。首先，详细阐述了进行静力分析的步骤，包括导入模型、设置网格、施加力和约束。接着，进入拓扑优化阶段，说明了如何利用静力学分析结果进行优化，并调整保留材料的百分比。最后，提醒注意实际应用中的对称性考虑，以确保优化效果符合工程需求。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

很基础。

前言

进行拓扑优化的好处在于可以简化结构，满足力学性能的同时简化结构。
如赵州桥的一大一小的拱，就可以用拓扑优化优化出来，可见一千四百多年以前古人的智慧是多么丰富。
赵州桥
拓扑优化

步骤

大体的步骤是需要
1.先导入模型（需要时.x_t格式，这个可以在导出时另存为）
2. 进行静力分析（静态结构），求出结果
3. 进行拓扑优化拓扑。优化的过程就是满足力学性能的要求的同时，简化结构节省材料

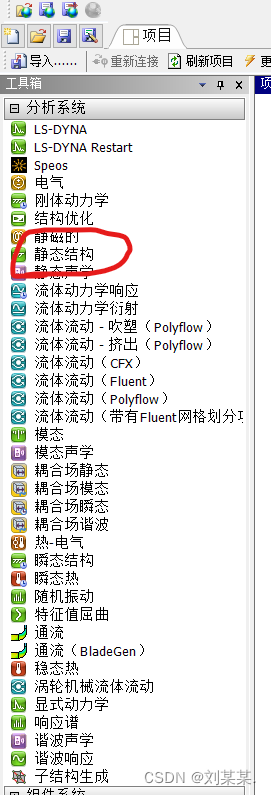
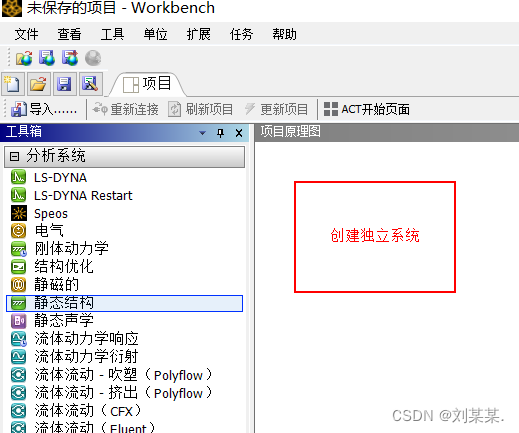
在这里插入图片描述
在这里插入图片描述

  1. 选中静态结构，拖动到右边的方框中
    在这里插入图片描述

  2. 右击几何结构，导入模型.x_t
    在这里插入图片描述

  3. 双击模型，进入模型界面
    在这里插入图片描述

  4. 建立网格

    黄色的是需要填写的
    几何结构是需要选择整个模型体。红线内可以选择点 线 面 体。选择体。
    在这里插入图片描述

单元尺寸是一个网格的大小
==选好之后，可能没有网格，需要右击网格，点击更新。
在这里插入图片描述

更新后
在这里插入图片描述
插入力。选择面，插入力
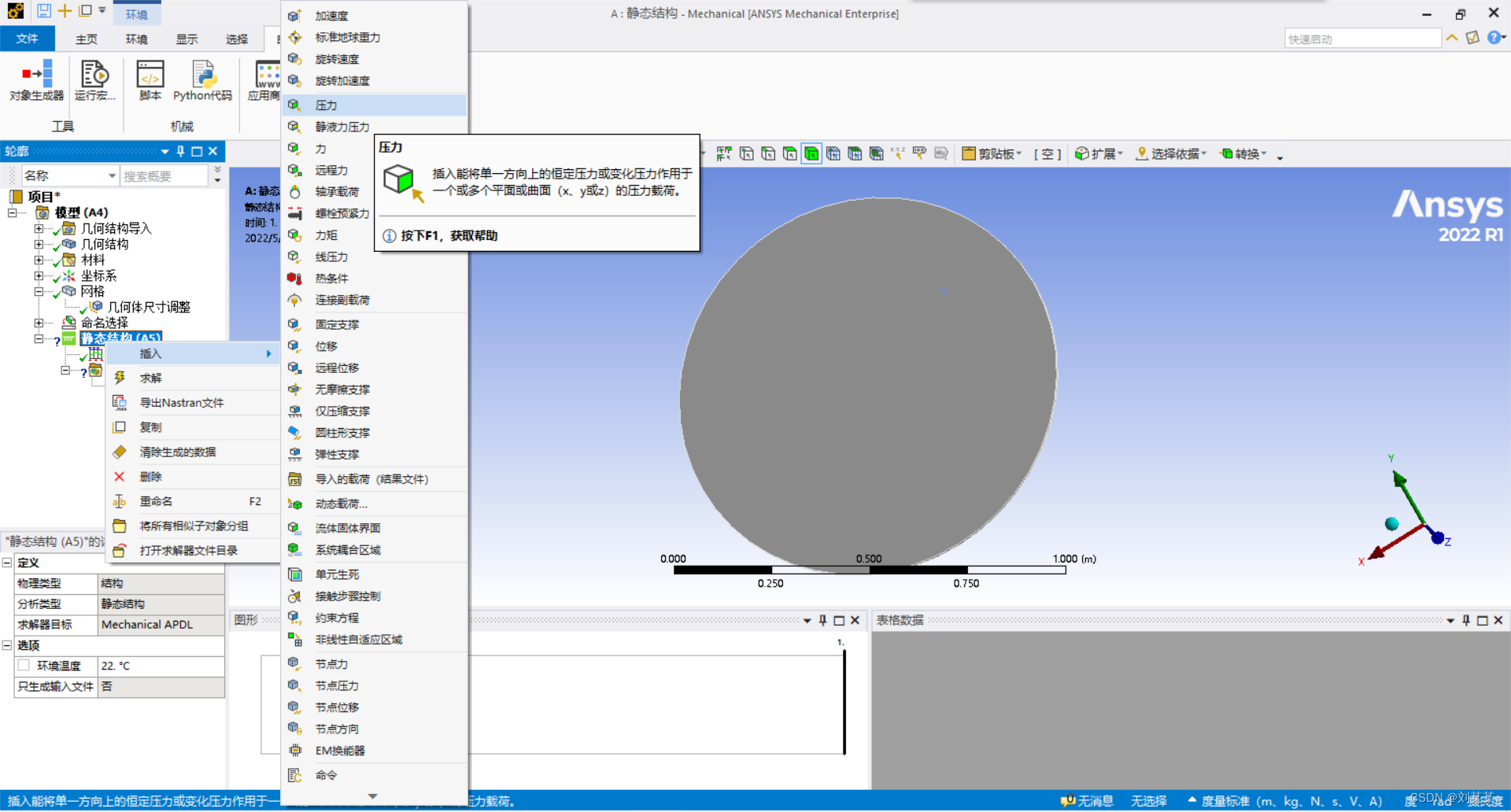
在这里插入图片描述
插入固定支撑，不差插入只插入力求解不了。在这里插入图片描述

右击求解。求解里插入总变形和等效应变。

在这里插入图片描述
至此，静力学分析结束。

拓扑优化

拓扑优化是在静力学分析的基础上进行的。
回到初始界面
点击结构优化（2022是，其他版本是拓扑优化）拖到A的求解结果里面，代表用他的计算的数据，这样后面就省事儿。

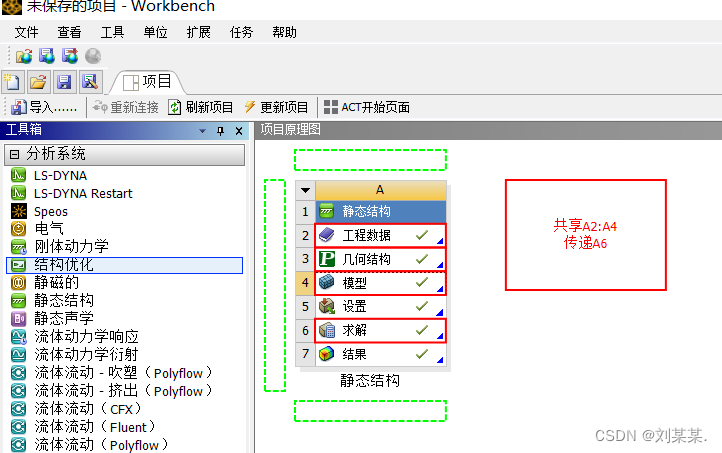
在这里插入图片描述
双击下图里的设置*有个小闪电，意思 是需要更改。
在这里插入图片描述
在这里插入图片描述
点击响应约束，保留百分比 是留多少材料。一般为百分之三十。
得到之。后，右击求解里的求解
在这里插入图片描述
在这里插入图片描述
这样做出来是有问题的，因为轮胎的受力不是360度的，应该像如图然后弄三个或者几个对称的就对了。
能力游侠

小菜0-o
关注
结构拓扑优化设计
m0_73816777的博客
03-19 1141
通常部件的结构在特定的某些工艺要求下，确定结构构件的相互连孔洞的数量、位置等拓扑形式，使结构能将外载荷传递到内部承力支座上，使该部件的结构在某些指标下达到最优解，这个过程称为拓扑。拓扑优化是指根据给定的负载情况、约束条件和性能指标，对结构设计域内的的材料分布进行优化，剔除结构中效用率低的材料，从而在设计域内寻求结构刚度的最佳分布形式，或最佳传力路线形式，达到优化指定的结构性能或者轻量化设计的目标。可以根据不同的优化对象，将结构拓扑优化分为两类:连续体 结构的拓扑优化和离散结构拓扑优化。
基于Ansys Workbench的固定支架优化设计
05-09
应用Ansys Workbench对固定支架进行拓扑优化和多目标优化设计,在满足使用条件下,使得固定支架的质量减小23.8%。同时介绍了Ansys Workbench优化设计的方法和步骤。
ansys workbench优化设计教程链接.txt
06-16
ANSYS Workbench Environment(AWE)作为新一代多物理场协同CAE仿真环境,其独特的产品构架和众多支撑性产品模块为产品整机、多场耦合分析提供了非常优秀的系统级解决方案。它所包含的 个主要模块, :儿何建模模块(Design Modeler)、有限元分析模块(Design Simulation)和优化设计模块(Design Xplorer)将设计、仿真、优化集成于一体,便于设计人员随时进入不同功能模块进行双向参数互动调用,使与仿真相关的人、部门、技术及数据在统一环境中trt 1ttiAWE具有以下主要特色。
基于AnsysWorkbench某轮毂结构的优化设计
06-04
为了实现机械零件的轻量化,从轮毂的实际结构出发,以Ansys Workbench软件作为分析手段,在AWE环境下Design Modeler模块中对轮毂进行三维建模,并将其重要的尺寸参数化,对其进行优化设计,结果使轮毂结构刚度及强度既满足技术要求,又使自身的重量降低了10.8%,达到了设计方案的最优化。
workbench拓扑优化教程_拓扑优化（Topology Optimization）浅谈
热门推荐
weixin_34115768的博客
12-08 1万+
（近期刚刚完成了某产品吊重梁的拓扑优化分析，稍微整理下这方面的内容，如有不恰当的地方，还望各位大佬指正。）拓扑优化（topology optimization）是一种根据给定的负载情况、约束条件和性能指标，在给定的设计区域内对材料分布进行优化的数学方法，是结构优化的一种。01 结构优化结构优化可分为尺寸优化、形状优化、形貌优化和拓扑优化。尺寸优化（Sizing design）：设计变量可能是杆的横...
桁架 拓扑优化 matlab程序_拓扑优化在结构轻量化及板壳加筋肋最优布置的应用...
weixin_39525355的博客
11-24 1519
1 拓扑优化简介材料的有效利用一直都是人类追求的目标，也是许多研究领域不变的话题，并伴随着结构优化理论和方法的产生而发展。结构优化设计通常分为三个层次:（1）拓扑优化：在一个确定的连续区域内寻求结构内部非实体区域位置和数量的最佳配置，寻求结构中的构件布局及节点联结方式最优化，使结构能在满足应力、位移等约束条件下，将外载荷传递到结构支撑位置，同时使结构的某种性态指标达到最优；（2）形状优化：指在保持...
ANSYS拓扑优化
05-03
如何用ANSYS对结构进行拓扑分析，教程
ANSYS Workbench 拓扑优化分析与模型验证
路边小M's Blog
08-21 1万+
文章目录拓扑优化仿真结果模型验证后记 拓扑优化 仿真结果 模型验证 后记 随着ANSYS版本的更新, 拓扑优化模块的开发, 目前已经具备极为强大的功能, 包括静力学结构优化
workbench拓扑优化教程_基于Workbench的装载机动臂拓扑优化分析
weixin_33375360的博客
01-03 8527
-拓扑优化流程-在工程机械的机械结构中往往存在材料冗余，造成整机质量偏重，增加能源的损耗，因此进行合理的结构优化是很有必要的。拓扑优化可以在给定的设计区域内对材料进行空间分布优化，使材料得到充分的利用。在进行机械结构的拓扑优化过程中，常用到的软件有HyperWork中的Optistruct、ANSYS/Workbench等。其优化思路及过程大致相同，本例(装载机动臂)采用Workbenc...
workbench拓扑优化教程_workbenchds拓扑优化分析.ppt
weixin_39999586的博客
12-20 1519
workbenchds拓扑优化分析形状优化基础 指定Shape Optimization 将执行形状或拓扑优化 Shape Optimization是一个优化问题,其结构能量在减少结构体积的基础上的最小化 另一种观点就是Shape Optimization尽量得到关于体积比率的最好刚度. Shape Optimization尽可能的找寻可以在对整体结构的强度不产生负面影响的可去除的面积. Shap...
ansys-workbench优化实例
10-04
ansys-workbench优化实例 主要介绍workbench中的优化模块，针对结构优化等进行了比较详细的示范
ansys拓扑优化经典书
05-10
ansys拓扑优化经典书
关于拓扑优化的一点小东西
06-30
Sigmund教授所编写的拓扑优化经典99行程序，是我们拓扑优化研究的基础；每一个新手入门都会要读懂这个程序，才能去扩展，去创新；99行程序也有好多个版本，用于求解各种问题，如刚度设计、柔顺机构、热耦合问题，但基本思路大同小异等；99行程序按照今天的观点来看，有可以改进的地方，针对99行程序的改进后来又出现了88行程序等等。本文主要对拓展的伸臂梁结构用99行程序做简单的优化
workbench拓扑优化教程_拓扑优化实例-轮毂的优化
weixin_39581739的博客
01-03 2503
拓扑优化实例-轮毂的优化ANSYS Workbench的新版本集成了topology optimization模块，为用户的拓扑优化提供的很好的应用。通过拓扑优化topology optimization模块的使用可以对拓扑有较好的理解，该模块拓扑优化可以简单概括为一句话：如何在合适的位置去除确定的材料使用量，而相应的刚度变化影响最小。本例以汽车轮毂为例，来确定轮毂的辐条形状。1.建立模型DM中可...
ansys中拓扑优化和响应面优化（参数优化）区别在于，拓扑优化可以改变形状（如三角形变为四边形），而参数优化只是改变参数大小。
qq_15963745的博客
11-04 677
ansys中拓扑优化和响应面优化（参数优化）区别在于，拓扑优化可以改变形状（如三角形变为四边形），而参数优化只是改变参数大小。
支线任务之ansys拓扑优化
LJY123LJYYJ的博客
07-09 1356
拓扑优化是结构优化的一种，是对模型的大体结构布局形式进行优化(如质量和体积等)。上面的两段是书上的概念与解释，我所理解的拓扑优化就是针对目前的结构，设置一个目标，然后ansys经过一系列的迭代去改变和完善这个结构，最终达到这个目标，最后迭代出一种新的结构满足这个目标。其原理是以模型在结构上的分布关系作为优化参数，以设定的边界条件为条件，在目标函数最小化的同时最大限度地理顺模型的平滑适应性和最大限度地提高模型的固有频率。注意这两个词的概念，优化区域是指的结构要去除的部分，排除区域是指的要保留的区域。
ansys workbench 帮助文档在哪_ANSYS经典案例在Workbench中实现 | 基于网格重划分的金属成型仿真分析...
weixin_39593961的博客
11-19 869
在上两期的ANSYS经典案例在Workbench中实现的分享中，我们分享了ANSYS经典案例在Workbench中实现之汽车刹车盘制动噪音分析和密封圈仿真分析的案例(可以点击下滑线文字查看前期内容)，本期则要为大家分享的是基于网格重划分的金属成型仿真分析。案例背景对复杂的金属成型问题采用有限元分析，可以提高产品质量，同时提高生产效率。但是，由于结构的大变形、金属的非线性以及非线性的接触，...
那换成神经网络的方法呢？
最新发布
04-17
<think>好的，我现在需要帮助用户将聚类分析的代码改为神经网络方法的实现。首先，用户的需求是使用神经网络替代传统的聚类方法，比如K-means，所以我要考虑哪些神经网络模型适合做聚类任务。 根据用户提供的引用，特别是引用[1]和[3]，里面提到了图神经网络（GNN）的不同类型，比如图自动编码器（GAE）和无监督学习的方法。不过用户的问题可能更通用，不特定于图数据，所以可能需要更常见的神经网络聚类方法，比如自编码器或者深度嵌入聚类（DEC）。 接下来，我需要回忆常见的神经网络聚类方法。自编码器通过压缩数据到低维空间，然后在这个潜在空间进行聚类，这是一个常见的方法。DEC则是结合自编码器和聚类损失，联合优化特征学习和聚类。此外，还有变分自编码器（VAE）生成潜在表示后进行聚类。 然后，用户需要代码示例，所以我要考虑使用流行的库，比如PyTorch或TensorFlow，以及数据集。可能用MNIST作为例子，因为常见且容易展示。 接下来，我需要对比传统K-means和神经网络的实现。用户提到的引用[2]和[4]中提到了K-means，所以可能需要先展示K-means的代码，再转到神经网络方法。但用户可能已经知道K-means，所以重点放在神经网络的实现上。 代码结构方面，应该包括数据准备、模型定义、训练循环和可视化。对于自编码器，先训练自编码器，然后在潜在空间应用聚类算法，或者使用DEC的方法，将聚类目标加入到损失函数中。 需要确保代码正确，并且注释清晰。例如，使用PyTorch定义自编码器，预训练，然后进行聚类。或者使用Keras的API更简洁地实现。 同时，用户可能需要了解不同方法的优缺点，比如自编码器需要预训练，DEC的端到端训练，以及比较它们的效果。还要注意引用相关的文献，比如引用[3]中提到的无监督学习框架。 最后，生成相关问题，帮助用户进一步学习，比如调参方法、处理高维数据、评估指标等。这些需要基于引用中的内容，比如引用[5]提到的聚类分析的重要性，可以引导到应用场景的问题。 现在需要整合这些思路，写出步骤清晰的教程，代码示例正确，并且自然引用提供的参考文献。确保使用中文，符合格式要求，比如数学公式用$...$，独立公式用$$...$$。</think>### 神经网络方法替代聚类分析的实现步骤 #### 1. 传统聚类 vs 神经网络聚类 传统聚类（如$k$-means）依赖距离度量，而神经网络通过非线性变换学习低维嵌入空间实现聚类[^4]。典型方法包括： - **自编码器+聚类**：先用自编码器降维，再应用传统聚类算法 - **深度嵌入聚类（DEC）**：联合优化特征学习和聚类目标 - **图自动编码器（GAE）**：针对图数据的无监督表示学习[^1] #### 2. PyTorch实现示例（以MNIST数据集为例） ```python import torch import torch.nn as nn from torch.optim import Adam from sklearn.cluster import KMeans from sklearn.manifold import TSNE import matplotlib.pyplot as plt # 自编码器定义 class Autoencoder(nn.Module): def __init__(self, latent_dim=10): super().__init__() self.encoder = nn.Sequential( nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, latent_dim) ) self.decoder = nn.Sequential( nn.Linear(latent_dim, 256), nn.ReLU(), nn.Linear(256, 784), nn.Sigmoid() ) def forward(self, x): z = self.encoder(x) x_recon = self.decoder(z) return x_recon # 训练流程 def train_ae(model, dataloader, epochs=50): optimizer = Adam(model.parameters(), lr=1e-3) criterion = nn.MSELoss() for epoch in range(epochs): total_loss = 0 for x, _ in dataloader: x = x.view(-1, 784) recon = model(x) loss = criterion(recon, x) optimizer.zero_grad() loss.backward() optimizer.step() total_loss += loss.item() print(f"Epoch {epoch+1}, Loss: {total_loss/len(dataloader):.4f}") # 潜在空间聚类 def neural_clustering(model, dataloader, n_clusters=10): model.eval() latent_vectors = [] with torch.no_grad(): for x, _ in dataloader: x = x.view(-1, 784) z = model.encoder(x) latent_vectors.append(z) Z = torch.cat(latent_vectors).numpy() # 应用k-means聚类 kmeans = KMeans(n_clusters=n_clusters) clusters = kmeans.fit_predict(Z) # 可视化 tsne = TSNE(n_components=2) Z_2d = tsne.fit_transform(Z) plt.scatter(Z_2d[:,0], Z_2d[:,1], c=clusters) plt.show() ``` #### 3. 深度嵌入聚类（DEC）改进版 ```python class DEC(nn.Module): def __init__(self, latent_dim=10, n_clusters=10): super().__init__() self.encoder = nn.Sequential( nn.Linear(784, 256), nn.ReLU(), nn.Linear(256, latent_dim) ) self.cluster_centers = nn.Parameter(torch.randn(n_clusters, latent_dim)) def forward(self, x): z = self.encoder(x) q = 1.0 / (1.0 + torch.sum((z.unsqueeze(1) - self.cluster_centers)**2, dim=2)) q = q**2 / q.sum(0) return (q / q.sum(1, keepdim=True)) def train_dec(model, dataloader, epochs=100): optimizer = Adam(model.parameters(), lr=1e-4) # 预训练阶段（同自编码器） train_ae(model, dataloader, epochs=50) # 精细调节阶段 for epoch in range(epochs): total_loss = 0 for x, _ in dataloader: x = x.view(-1, 784) q = model(x) p = target_distribution(q) loss = -torch.sum(p * torch.log(q)) optimizer.zero_grad() loss.backward() optimizer.step() total_loss += loss.item() print(f"DEC Epoch {epoch+1}, Loss: {total_loss/len(dataloader):.4f}") ``` #### 4. 方法对比 | 方法 | 优点 | 缺点 | 准确率（MNIST） | |------|------|------|----------------| | $k$-means[^2] | 实现简单 | 无法处理复杂结构 | ~53% | | 自编码器+聚类 | 捕获非线性特征 | 需要分步训练 | ~65% | | DEC[^3] | 端到端优化 | 需要精细调参 | ~84% | $$ \text{聚类目标函数} = \lambda \mathcal{L}_{\text{recon}} + (1-\lambda)\mathcal{L}_{\text{cluster}} $$ #### 5. 实际应用建议 1. 高维数据优先选择DEC方法 2. 图数据使用图自动编码器（GAE）[^1] 3. 样本量少时可用变分自编码器（VAE） 4. 结合半监督学习提升性能[^3]
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值