线性DP例题

琛_

已于 2022-01-25 09:59:12 修改

阅读量282

点赞数

分类专栏：动态规划文章标签：动态规划算法 c++

于 2022-01-19 12:11:04 首次发布

本文链接：https://blog.csdn.net/qq_45896050/article/details/122575730

版权

动态规划专栏收录该内容

7 篇文章 0 订阅

订阅专栏

线性DP例题

最长上升子序列
最长公共子序列
数字三角形
最短编辑距离
编辑距离
拦截导弹
摘花生
最大上升子序列和

没搞明白

最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

输入格式
第一行包含整数 N。

第二行包含 N 个整数，表示完整序列。

输出格式
输出一个整数，表示最大长度。

数据范围
1 ≤ N ≤ 1000，
−10^9 ≤ 数列中的数 ≤ 10^9

输入样例：

7 
3 1 2 1 8 5 6

输出样例：

状态表示 f[i]

集合： f[i]表示从第一个数字开始算，以第i个数字结尾的最大的上升序列。
属性：集合中的子序列长度的最大值
状态计算
枚举上升子序列的倒数第二数，不妨以坐标j表示，若 a[j] < a[i] 则 f[i] =max(f[i], f[j] + 1)
备注
有一个边界，若前面没有比i小的，f[i]为1（自己为结尾）

#include <iostream>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++ ) cin >> a[i];
	for (int i = 1; i <= n; i ++ ) {
		f[i] = 1;
		for (int j = 1; j < i; j ++ ) 
			if (a[i] > a[j])
				f[i] = max(f[i], f[j] + 1);		
	} 
	int res = 0;
	for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
	cout << res;
	return 0;
}

最长公共子序列

给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

输入格式
第一行包含两个整数 N 和 M。

第二行包含一个长度为 N 的字符串，表示字符串 A。

第三行包含一个长度为 M 的字符串，表示字符串 B。

字符串均由小写字母构成。

输出格式
输出一个整数，表示最大长度。

数据范围
1 ≤ N,M ≤ 1000

输入样例：

4 5
acbd
abedc

输出样例：

在这里插入图片描述
可以将题目分为两半考虑，按照序列末尾的字符是不是相等来区分。

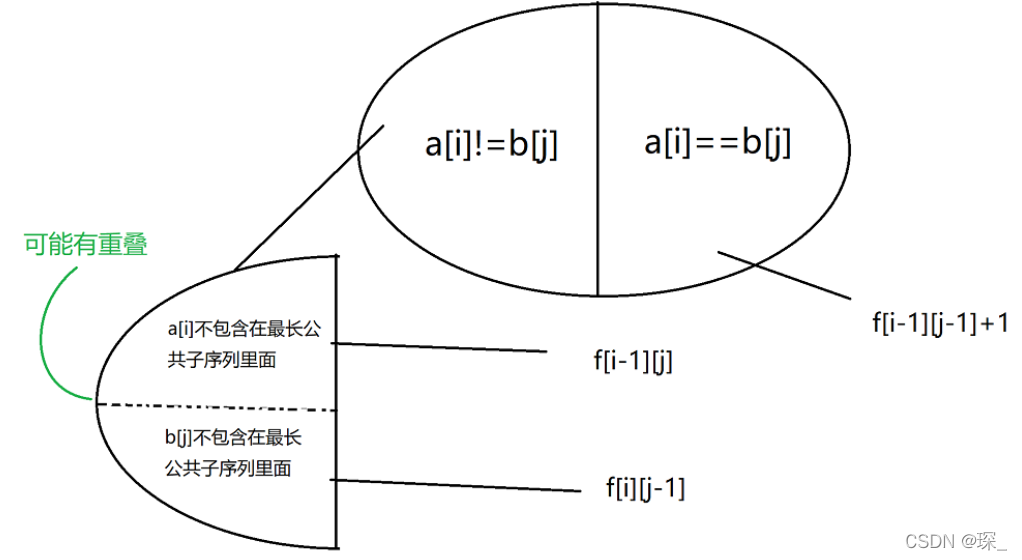
如果两个字符相等，就可以直接转移到 f[i-1][j-1]
不相等的话，两个字符一定有一个可以抛弃，可以对 f[i-1][j], f[i][j-1] 两种状态取max来转移

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
	cin >> n >> m >> a + 1 >> b + 1;
	for (int i = 1; i <= n; i ++ ) 
		for (int j = 1; j <= m; j ++ ) {
			if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1;
			else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
		}
	cout << f[n][m];
	return 0;
}

数字三角形

给定一个如下图所示的数字三角形，从顶部出发，在每一结点可以选择移动至其左下方的结点或移动至其右下方的结点，一直走到底层，要求找出一条路径，使路径上的数字的和最大。

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

输入格式
第一行包含整数 n，表示数字三角形的层数。

接下来 n 行，每行包含若干整数，其中第 i 行表示数字三角形第 i 层包含的整数。

输出格式
输出一个整数，表示最大的路径数字和。

数据范围
1≤n≤500,
−10000≤三角形中的整数≤10000

输入样例：

输出样例：

// 正序，考虑边界问题
#include <iostream>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f3f3f3f3f;
int n;
int a[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++ ) 
		for (int j = 1; j <= i; j ++ ) 
			cin >> a[i][j];
	
	for (int i = 2; i <= n; i ++ )
		for (int j = 1; j <= i; j ++ ) {
			if (j == 1) a[i][j] += a[i - 1][j];
			else if(j == i) a[i][j] += a[i - 1][j - 1];
			else a[i][j] += max(a[i - 1][j - 1], a[i - 1][j]); 
		}
		
	int res = - INF;
	for (int i = 1; i <= n; i ++ ) res = max(res, a[n][i]);
	cout << res;		
	return 0;
}
// 倒序，不必考虑边界问题
#include <iostream>
using namespace std;
const int N = 510;
int n;
int a[N][N];
int main()
{
	cin >> n;
	for (int i = 1; i <= n; i ++ ) 
		for (int j = 1; j <= i; j ++ ) 
			cin >> a[i][j];
	
	for (int i = n - 1; i >= 1; i -- ) 
		for (int j = 1; j <= i; j ++ )
			a[i][j] += max(a[i + 1][j], a[i + 1][j + 1]);
	
	cout << a[1][1];
	return 0;
}

最短编辑距离

给定两个字符串 A 和 B，现在要将 A 经过若干操作变为 B，可进行的操作有：

删除–将字符串 A 中的某个字符删除。
插入–在字符串 A 的某个位置插入某个字符。
替换–将字符串 A 中的某个字符替换为另一个字符。
现在请你求出，将 A 变为 B 至少需要进行多少次操作。

输入格式
第一行包含整数 n，表示字符串 A 的长度。

第二行包含一个长度为 n 的字符串 A。

第三行包含整数 m，表示字符串 B 的长度。

第四行包含一个长度为 m 的字符串 B。

字符串中均只包含大写字母。

输出格式
输出一个整数，表示最少操作次数。

数据范围
1 ≤ n,m ≤ 1000

输入样例：

10 
AGTCTGACGC
11 
AGTAAGTAGGC

输出样例：

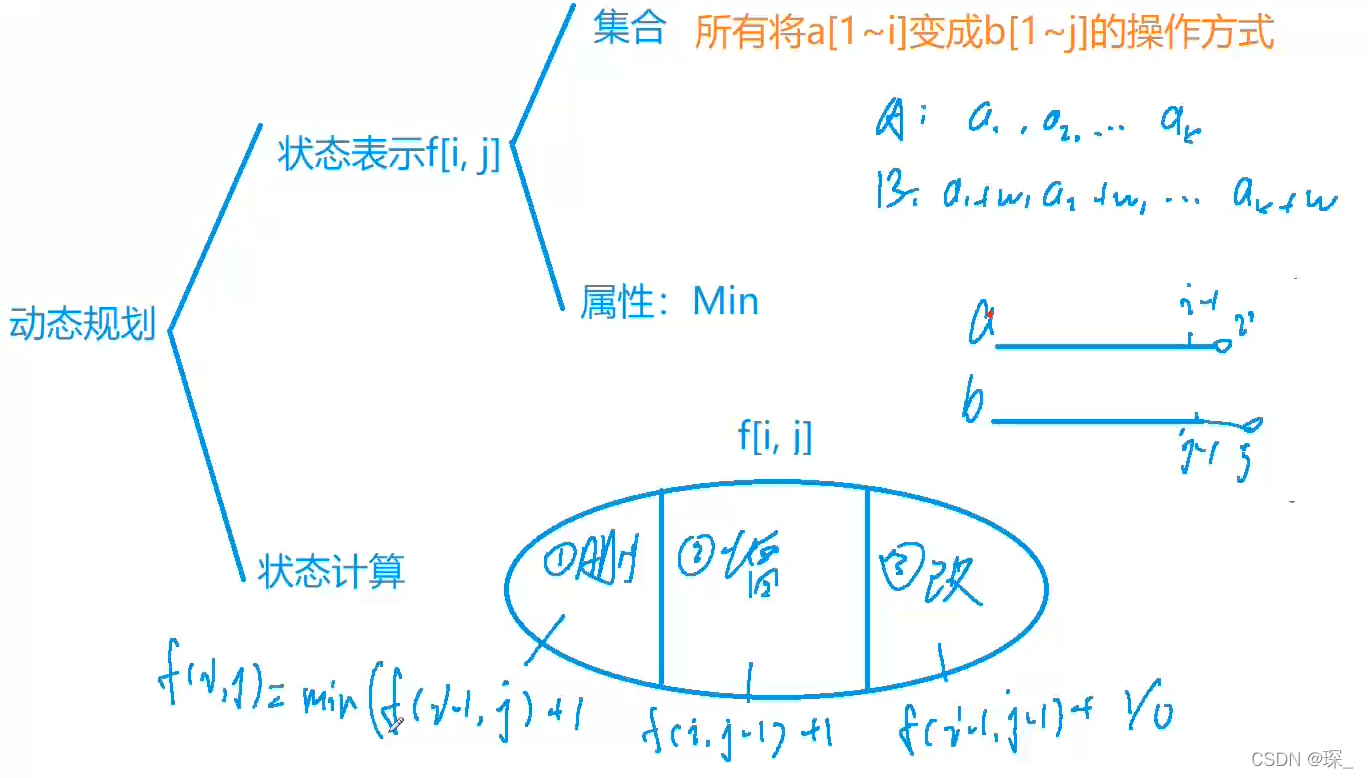
在这里插入图片描述
对增加操作的理解

遍历的a数组的每个元素都是已经存在的，所以增加操作只能在a[i]的后面进行，而不能在位置 i进行，我们讨论的是在最后一个位置 i 进行什么样的操作能使a[1~i] 等于b[1~j]，但不是对这个位置本身进行操作，增加的不是这个位置上的数。

f[i][j] 指的是将a[1 ~ i]变成b[1 ~ j]的操作数，不是真的将a[1 ~ i]的每一位变成b[1 ~ j]的每一位，而是以a[1 ~ i]为起点，b[1 ~ j]为终点的变化次数。

增加那一步的操作为什么是f[i][j] = f[i][j - 1] + 1，按照y总那个方案确实不好理解，我最开始一直理解的f[i][j]是让a[1 ~ i] 等于b[1 ~ j]的最小操作步骤，按照这个思路，如果最后一步是增加，那一定是a[i] = b[j] -> a[i - 1] = b[j - 1]，所以转移方程为f[i][j] = f[i - 1][j - 1] + 1，但是实际上不能这么理解，我在力扣上看到另一种理解方式，很通俗，首先我们要知道，题目让我们求的是编辑距离，然后：

最后一步是增加：若最后一步是增加，为了使a[1 ~ i] = b[1 ~ j]那最后一步增加的一定是b[j]。那么f[i][j]就可以看成是，首先将a[1 ~ i]转化成b[1 ~ j - 1]，这时候所操作的步骤数为f[i][j - 1]，下一步在b[j - 1]后面添加一个b[j]，那么f[i][j] = f[i][j - 1] + 1。也就是说，我们的转化过程为：a[1 ~ i] -> b[1 ~ j - 1] -> b[1 ~ j]，f[i][j]的意义是将a[1 ~ i]转化为b[1 ~ j]的步骤数，不能理解为直接在a[i]后面添加一个数，这是一个动态的变化的过程。
最后一步是删除：按照上面的理解，若最后一步是删除，那我们最后删除的一定是a[i]，我们可以做这样的操作：a[1 ~ i] -> a[1 ~ i - 1] -> b[1 ~ j]，也就是先将a的最后一位删掉，将剩余的部分变为b，那么f[i][j] = 1 + f[i - 1][j]。
最后一步是替换：按照上面的理解，若最后一步是替换，那一定是将a[i]替换为b[j]，这时候我们可以做这样的操作：a[1 ~ i - 1, i] -> b[1 ~ j - 1] + a[i] -> b[1 ~ j]，也就是将a的前i - 1个数先转化为b的前j - 1个数，最后将a[i] - > b[j]，若此时a[i] == b[j]，我们就不需要做最后一步转化，否则需要。这时候f[i][j] = f[i - 1][j - 1] + (int)(a[i] == b[j])。

总的来说，将f[i][j]理解为变换的次数更好理解，不要理解为最后一次操作。

细节问题：初始化
先考虑有哪些初始化

你看看在for遍历的时候需要用到的，但是事先没有的
（往往就是什么0啊1啊之类的）就要预处理
如果要找min的话别忘了INF
要找有负数的max的话别忘了-INF

本题对应：

f[0][i]如果a初始长度就是0，那么只能用插入操作让它变成b，则需要操作数 i
f[i][0]同样地，如果b的长度是0，那么a只能用删除操作让它变成b，则需要操作数 i
f[i][j] = INF //虽说这里没有用到，但是把考虑到的边界都写上还是保险

#include <iostream>
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
	cin >> n >> (a + 1);
	cin >> m >> (b + 1);
	for (int i = 1; i <= m; i ++ ) f[0][i] = i;
	for (int j = 1; j <= n; j ++ ) f[j][0] = j;
	for (int i = 1; i <= n; i ++ ) 
		for (int j = 1; j <= m; j ++ ) {
			f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
			if (a[i] == b[j]) f[i][j] = min(f[i][j], f[i - 1][j - 1]);
			else f[i][j] = min(f[i][j], f[i - 1][j - 1] + 1);
		}
	cout << f[n][m];
	return 0;
}

编辑距离

给定 n 个长度不超过 10 的字符串以及 m 次询问，每次询问给出一个字符串和一个操作次数上限。

对于每次询问，请你求出给定的 n 个字符串中有多少个字符串可以在上限操作次数内经过操作变成询问给出的字符串。

每个对字符串进行的单个字符的插入、删除或替换算作一次操作。

输入格式
第一行包含两个整数 n 和 m。

接下来 n 行，每行包含一个字符串，表示给定的字符串。

再接下来 m 行，每行包含一个字符串和一个整数，表示一次询问。

字符串中只包含小写字母，且长度均不超过 10。

输出格式
输出共 m 行，每行输出一个整数作为结果，表示一次询问中满足条件的字符串个数。

数据范围
1 ≤ n,m ≤ 1000,

输入样例：

3 2
abc
acd
bcd
ab 1
acbd 2

输出样例：

1
3

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1010;
int n, m;
char a[N][20];
int f[N][N];
int dist(char a[], char b[]) 
{
	int la = strlen(a + 1);
	int lb = strlen(b + 1);
	for (int i = 1; i <= lb; i ++ ) f[0][i] = i;
	for (int i = 1; i <= la; i ++ ) f[i][0] = i; 
	for (int i = 1; i <= la; i ++ ) 
		for (int j = 1; j <= lb; j ++ ) {
			f[i][j] = min(f[i - 1][j] + 1, f[i][j - 1] + 1);
			f[i][j] = min(f[i][j], f[i - 1][j - 1] + (a[i] != b[j]));
		}
	return f[la][lb];
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i ++ ) cin >> (a[i] + 1);
	while (m -- ) {
		char s[20];
		int b, res = 0;
		cin >> (s + 1) >> b;
		for (int i = 1; i <= n; i ++ ) 
			if (dist(a[i], s) <= b) 
				res ++ ;
		cout << res << endl;  
	}
	return 0; 
}

拦截导弹

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。

但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。

某天，雷达捕捉到敌国的导弹来袭。

由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入格式
共一行，输入导弹依次飞来的高度。

输出格式
第一行包含一个整数，表示最多能拦截的导弹数。

第二行包含一个整数，表示要拦截所有导弹最少要配备的系统数。

数据范围
雷达给出的高度数据是不大于 30000 的正整数，导弹数不超过 1000。

输入样例：

389 207 155 300 299 170 158 65

输出样例：

6
2

没懂怎么用贪心求系统数

第一问：最长不下降子序列长度，不再赘述。

第二问：能覆盖整个序列的最少的不上升子序列的个数

贪心：
用如下方式维护数组s，数组长度cnt，意为cnt个不下降子序列。保存的是每一个不上升子序列中的最后一个数：
遍历原序列，对于遍历到的每一个数x：

若x大于s中每一个数，则新建一个不上升子序列，放入x;
否则，找到s中大于等于x的最小的数，将其替换。

由于s每次增加长度时，增加的数必然大于其前面s中的任何一个数；且每次替换时，不改变x与被替换数左右相邻两数的相对大小关系，故s必然维持单调递增。则s即为原序列的最长上升子序列。

即证明了：
“能覆盖整个序列的最少的不上升子序列的个数”等价于“该序列的最长上升子序列长度”
同理即有：
“能覆盖整个序列的最少的不下降子序列的个数”等价于“该序列的最长下降子序列长度”
（欲深究可研读离散数学中的Dilworth定理）

下面证明上述贪心算法的正确性：
设A为用该贪心算法得到的方案，B为最优解方案。记A的不上升子序列个数为la，B的不上升子序列个数为lb。
显然lb<=la（否则B就不是最优解）。
故只需证明la>=lb。用调整法(微调法)。
若A=B，则la=lb，显然成立。
否则（即A!=B），必然可以找到两方案中第一个(以原序列的顺序)不同之处（某数放在了不同的位置，且原序列中该数前的所有数在两方案中放的位置皆相同），将该数在两方案中所处的位置上的数(即该数本身)以及两位置之后方案中的序列相互对调，结果所得方案仍为合法解。即我们将贪心算法所得方案调整成了最优方案，且在调整过程中，方案的序列数没有增加，故la>=lb（la -> lb，且la转变为lb的过程中la的大小没有增加）。
证毕！

#include <iostream>
using namespace std;
const int N = 1010;
int a[N], n;
int f[N], g[N];
int main()
{
	while (cin >> a[n]) n ++ ;
	
	int res = 0;
	for (int i = 0; i < n; i ++ ) {
		f[i] = 1;
		for (int j = 0; j < i; j ++ ) 
			if (a[i] <= a[j])
				f[i] = max(f[i], f[j] + 1);
		res = max(res, f[i]);
	}
	cout << res << endl;
	
	int cnt = 0;
	for (int i = 0; i < n; i ++ ) {
		int k = 0;
		while (k < cnt && g[k] < a[i]) k ++ ;
		g[k] = a[i];
		if (k >= cnt) cnt ++ ;
	}
	cout << cnt;
	
 	return 0;
}

摘花生

Hello Kitty想摘点花生送给她喜欢的米老鼠。

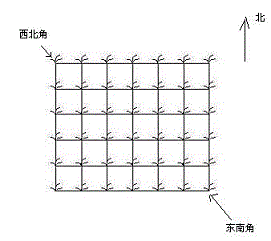
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

输入格式
第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式
对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围
1 ≤ T ≤ 100,
1 ≤ R,C ≤ 100,
0 ≤ M ≤ 1000

输入样例：

输出样例：

8
16

#include <iostream>
using namespace std;
const int N = 110;
int n;
int f[N][N];
int main()
{
	cin >> n;
	while (n -- ) {
		int a, b;
		cin >> a >> b;
		for (int i = 1; i <= a; i ++ ) 
			for (int j = 1; j <= b; j ++ )
				cin >> f[i][j];
		for (int i = 1; i <= a; i ++ ) 
			for (int j = 1; j <= b; j ++ ) 
				f[i][j] += max(f[i][j - 1], f[i - 1][j]);
		cout << f[a][b] << endl;	
	}
	return 0;
}

最大上升子序列和

一个数的序列 bi，当 b1<b2<…<bS 的时候，我们称这个序列是上升的。

对于给定的一个序列(a1,a2,…,aN)，我们可以得到一些上升的子序列(ai1,ai2,…,aiK)，这里1≤i1<i2<…<iK≤N。

比如，对于序列(1,7,3,5,9,4,8)，有它的一些上升子序列，如(1,7),(3,4,8)等等。

这些子序列中和最大为18，为子序列(1,3,5,9)的和。

你的任务，就是对于给定的序列，求出最大上升子序列和。

注意，最长的上升子序列的和不一定是最大的，比如序列(100,1,2,3)的最大上升子序列和为100，而最长上升子序列为(1,2,3)。

输入格式
输入的第一行是序列的长度N。

第二行给出序列中的N个整数，这些整数的取值范围都在0到10000(可能重复)。

输出格式
输出一个整数，表示最大上升子序列和。

数据范围
1 ≤ N ≤ 1000

输入样例：

7
1 7 3 5 9 4 8

输出样例：

(线性DP) O(n2)
状态表示：
f[i] 表示前i个数中的最大子序列和

状态转移：
对于每一个小于a[i]的a[j] (j < i)
f[i] = max(f[i], f[j] + a[i])

时间复杂度
状态总个数等于数列总长度N, 计算每一个状态需要枚举前i个数，所以总复杂度为O(n^2)

#include <iostream>
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
	cin >> n;
	// 初始化f意义：每一个数字都是一个上升子序列
	// 初始化时，自然本身就是其和
	for (int i = 1; i <= n; i ++ ) cin >> a[i], f[i] = a[i];
	for (int i = 2; i <= n; i ++ ) 
		for (int j = 1; j < i; j ++ ) 
			if (a[j] < a[i])
				f[i] = max(f[i], f[j] + a[i]);
	int res = -1;
	for (int i = 1; i <= n; i ++ ) res = max(res, f[i]);
	cout << res;
	return 0;
}