线性代数之 奇异值分解 svd

目录

一、SVD

◼ 奇异值分解是什么

◼ 杂讯过滤

二、SVD的求解过程

举例

---

参考3.SVD 分解_哔哩哔哩_bilibili

奇异值分解是什么（中英文字幕）_哔哩哔哩_bilibili

 

一、SVD

◼ 奇异值分解是什么

假设我们给出一个矩阵A，来观察这个矩阵在做什么，我们可以想象它是如何转换不同向量的，

现在我们假设要找到一组正交向量，当A被变换时，将保持正交。

在二维中实现它的一种方法是从一组正交向量开始，然后继续旋转它们，所以我们注意到它们相应的变换也是正交的，在这里，这个矩阵A似乎不存在这样一组向量，

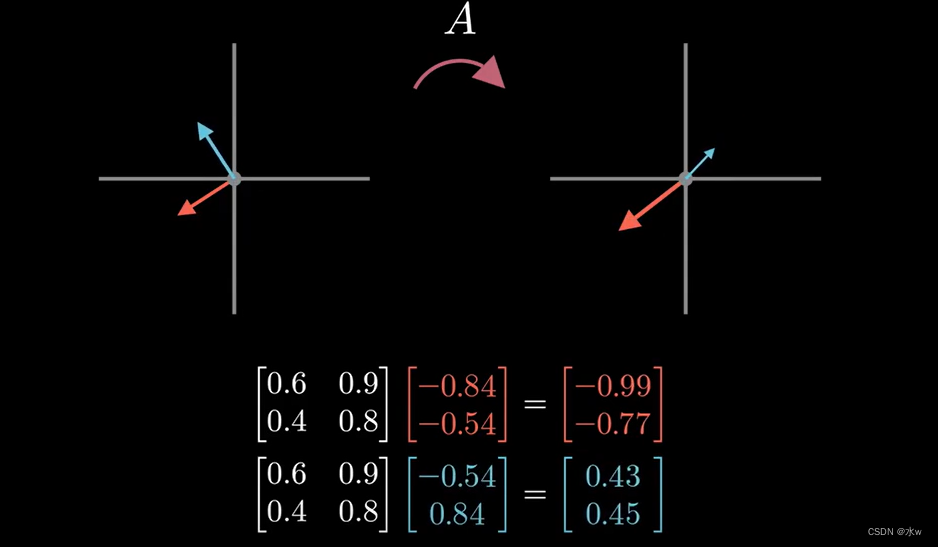
但我们并不能真正看到所有的变换向量，因为它们有些太小了。

这一次，我们在绘制变换向量之前对其进行归一化，就这个（如下图），我们找到了一组正交向量被A变换之后仍保持正交，这组向量定义了奇异值分解。

现在，如果我们想在更高的维度做这件事，那么这种搜索方式会变得需要大量计算，让我们看看是否能找到一个很好的解决方案？（它不涉及搜索）

首先，重申一下我们的问题，

我们想找到一组正交向量，它在我们的矩阵变换（A）时仍保持正交。

 

在二维中，意味着我们要找到v1,v2，以及y1,y2。让我们把y分成一个方向和大小，所以u1和u2时单位向量，

为了使这个分析更具有一般性，我们可以把问题改写成矩阵形式，

现在我们的目标是求解U和V，它们是正交矩阵。如果我们能找到这些正交矩阵，那么我们说我们发现了原始矩阵A的奇异值分解。它被分解的原因是，因为我们可以用UE和V来重写A（U，V是正交矩阵），

好的，现在看看我们是否能求解U和V，首先我们两边乘以转置，然后展开这些项，

• 因为我们要找到U是一个正交矩阵，我们可以进行抵消U和UT；
• 因为E是对角阵，我们可以把对角线上的所有项进行平方；

现在我们开始注意到一下有趣的事情，由于V是由ATA的本征分解得到的，因为ATA是对称的，所以满足了V是正交的条件（性质：对称矩阵的特征向量是正交的）。

类似的，我们可以通过将等式右乘A的转置来得到U，

让我们总结一下目前的情况，我们想找到一个U和一个V，

• 它们满足这个表达式，
• 它们也是正交的，

我们发现ATA的本征分解会给我们一个正交矩阵V，同样的，我们发现AAT的本征分解将给我们一个正交矩阵U。

 最后要注意到的是我们也从本质上证明了矩阵ATA和AAT的特征值是相同的，因为在这两种情况下，我们都是从最初的等式开始的，然后让右边看起来像特征值为E^2的特征分解，这是奇异值分解的一个有趣的性质。

它回答了一下问题：

（1）我们的矩阵哪个方向能够最大拉伸单位向量。

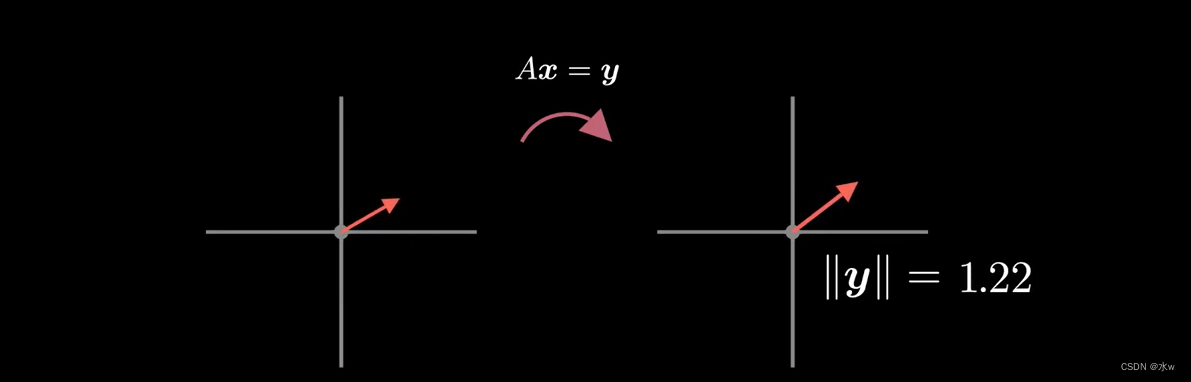
用数学术语来说，SVD解决了这个优化问题。

要知道为什么，让我们先把这个问题转化为这个，两者是等价的，因为找到一个最大长度变换的x，与找到一个最大平方长度变换的x，两者相同。

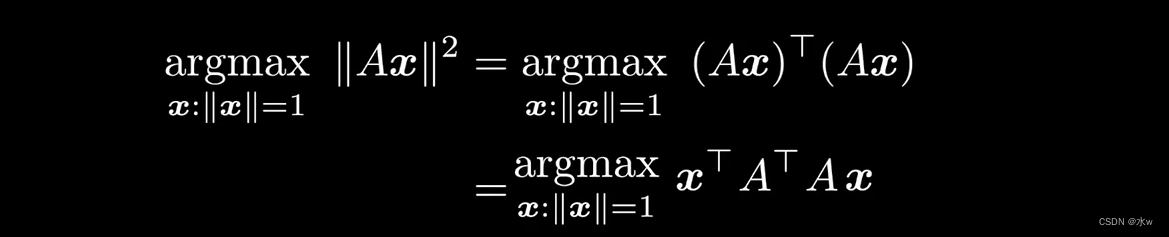
现在我们写出矩阵ATA的特征值方程，因为x是单位向量，我们可以抵消xTx，

所以最大化xT(ATA)x等于最大化拉姆达，

为了最大化拉姆达，我们可以简单的选择x，作为具有最大对应特征值的特征向量。

如果你还记得的话，矩阵U的行就是ATA的特征向量，所以ATA的特征向量有对应的最大特征值将成为U的第一行。

所以，再来一次， 我们可以使用奇异值分解不用搜索就能解决这一问题。这就是为什么奇异值分解是一种非常有用的矩阵分解。

 

SVD(Singular Value Decomposition, 奇异值分解)是线性代数中既优雅又强大的工具, 它揭示了矩阵最本质的变换. 使用SVD对矩阵进行分解, 能得到代表矩阵最本质变化的矩阵元素. 这就好比一个合数能表示为若干质数之积, 分解合数能得到表示该合数的质因数; 复杂周期信号可以表示为若干简单的正弦波和余弦波之和, 使用傅里叶变换能得到表示该信号的简单波; 复杂矩阵所代表的线性变换可由若干个简单矩阵所代表的线性变换组合起来, 使用SVD能找到这些简单矩阵.

◼ 杂讯过滤

左图中矩阵有格子数：15x25，那么我们怎么表示这个图，记录矩阵的样子呢？其实不难看出，是由右侧这三种矩阵组成的，只要记录这三列表示即可。

我们可以看到上图中有一些杂讯（灰色格子），那么来做SVD分解时，我们会记录到它会有很多不同的奇异值，

意思也就是原本可以拆成15个奇异值相加，可是重点是前面三个奇异值的倍率比较高，那么我们如果只用前面三个奇异值来计算M，

那么结果会怎么样呢？我们会得到一个很好的近似，虽然这个近似与原本的M不准，不是完全一样，但是不准的部分很高的可能是杂讯。

 这就说明，通过SVD分解，有时候会省略一下资讯，但是这些资讯其实就是我们不要的。

 

二、SVD的求解过程

那SVD具体如何求解呢?

 

举例