👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
ADMM算法,该方法适合求解大规模优化问题,特别是在机器学习和统计优化中的一些模型。近年来,经过学者们的潜心研究和不断改进,ADMM算法在理论体系方面更加完善,算法性能也得到了很大的改进。由于ADMM算法具有独特的优势,可以在大数据的背景下并行处理大规模优化问
题,所以在机器学习、统计优化、图像处理和其它领域都能发挥很大的作用。
适用于机器学习和统计学习相关问题。该算法可以将规模较大且复杂的全局问题分解成多个规模较小、容易求解的局部子问题。ADMM算法主要基于增广拉格朗日乘子法(Agumented Lagrangians Method, ALM)和对偶上升算法.
ADMM算法的子问题求解,一个子问题可以利用邻近点映射性质,直接给出显式表达式,另一个子问题选择随机拟牛顿算法求解,使用泰勒展开式逼近海瑟矩阵的逆。2007年,Schraudolph等[39] 首次提出随机拟牛顿法,在求解随机凸优化问题时优于以往的算法,未证明算法的收敛性。2009 年Bordes等[6] 将随机梯度法和拟牛顿法相结合,求解大规模优化问题时表现很好,与梯度法相比,可以以更少的迭代步数,达到相同的精度。2014年Mokhtari和Ribeiro[31] 提出正则化随机拟牛顿优化算法,该方法在求解海瑟矩阵时,对相邻两步海瑟矩阵的高斯信息熵进行了正则化处理,改进了曲率对和海瑟矩阵的更新格式,使得算法收敛速度加快且更加稳定,且在目标函数强凸,海瑟矩阵特征值有上下界的条件下,证明了算法在期望意义下次线性收敛。2015年Mokhtari和Ribeiro[30] 提出了有限内存的随机拟牛顿法,在函数强凸,海瑟矩阵特征值有上下界的情况下,算法以概率1收敛到最优解,且在期望意义下次线性收敛。2016年,Moritz,Nishihara,Jordan[9] 提出了线性收敛的随机拟牛顿算法,该算法在大规模凸问题和非凸问题中均表现良好,精度比较高,在目标函数强凸,海瑟矩阵特征值有上下界的情况下,算法线性收敛。
基于对称ADMM的正不定近端项正则化研究解析
一、对称ADMM的基本原理与改进动机
对称ADMM(Symmetric ADMM)是经典ADMM算法的重要变体,其核心在于通过对称矩阵的引入优化迭代结构,从而加速收敛。传统ADMM通过交替更新原始变量和对偶变量分解优化问题,而对称ADMM在每次迭代中两次更新乘子,形成更稳定的收敛路径。例如,He等人提出的双步更新方法,通过调整参数范围保证了算法的全局收敛性,其收敛速度可达O(1/t)O(1/t)(遍历意义上的平均收敛)。对称ADMM的数学形式可视为Peaceman-Rachford分裂法的对偶应用,但其收敛性在非对称参数下通常难以保证。
二、正不定近端项正则化的作用机制
在对称ADMM框架中,正不定近端项正则化的引入旨在增强算法对非凸或非光滑问题的适应性。其核心迭代公式扩展为:

三、正则化方法在ADMM中的应用案例
- 图像处理:在TV(Total Variation)正则化图像去噪中,ADMM通过分裂目标函数为保真项与正则项,结合对称更新策略,显著提升去噪精度。例如,结合小波框架与TV的多参数模型,通过ADMM实现图像细节保留与噪声抑制的平衡。
- 信号处理:在雷达测距剖面重建中,ADMM结合卷积神经网络(CNN)作为正则化器,通过端到端训练提升反演质量,其MSE性能优于传统模型驱动方法。
- 分布式优化:在配电网无功控制中,自适应超松弛惩罚参数的对称ADMM相比传统一致性ADMM,在收敛速度与解的质量上表现更优,尤其适用于高维分布式问题。
四、正不定近端项的正则化潜在问题
- 收敛性挑战:正不定矩阵导致目标函数非凸,经典凸优化理论失效,需基于Kurdyka-Łojasiewicz(KL)框架或驻点理论分析收敛性。例如,非凸ADMM的变量序列需证明其子序列收敛至满足KKT条件的点。
- 参数敏感性:正则化权重λλ的选择需权衡稀疏性与偏差,过大易陷入局部最优,过小则无法有效正则化。渐进式调整策略(如逐步增加λλ)可缓解此问题。
- 计算复杂度:正不定矩阵的逆运算可能增加迭代成本,需结合预条件技术或近似求解(如线性化ADMM)降低复杂度。
五、研究展望与未来方向
- 理论深化:需建立更通用的收敛性框架,尤其是针对非光滑与非凸混合问题的分析,如结合Bregman距离或随机ADMM扩展应用范围。
- 算法优化:开发自动化参数选择策略(如基于机器学习的自适应调参),并探索低秩或稀疏矩阵结构以降低存储与计算开销。
- 跨领域应用:在量子优化、联邦学习等新兴场景中验证对称ADMM的潜力,例如分布式隐私保护优化中的正则化设计。
六、总结
基于对称ADMM的正不定近端项正则化方法通过引入灵活的矩阵调整机制,显著提升了传统算法在非凸优化中的适应性与效率。尽管在参数选择与理论分析上仍存挑战,其在图像重建、信号处理等领域的成功应用展示了广阔前景。未来的研究需在理论严谨性与计算效率间寻求平衡,推动该技术向更复杂的工程问题拓展。
📚2 运行结果
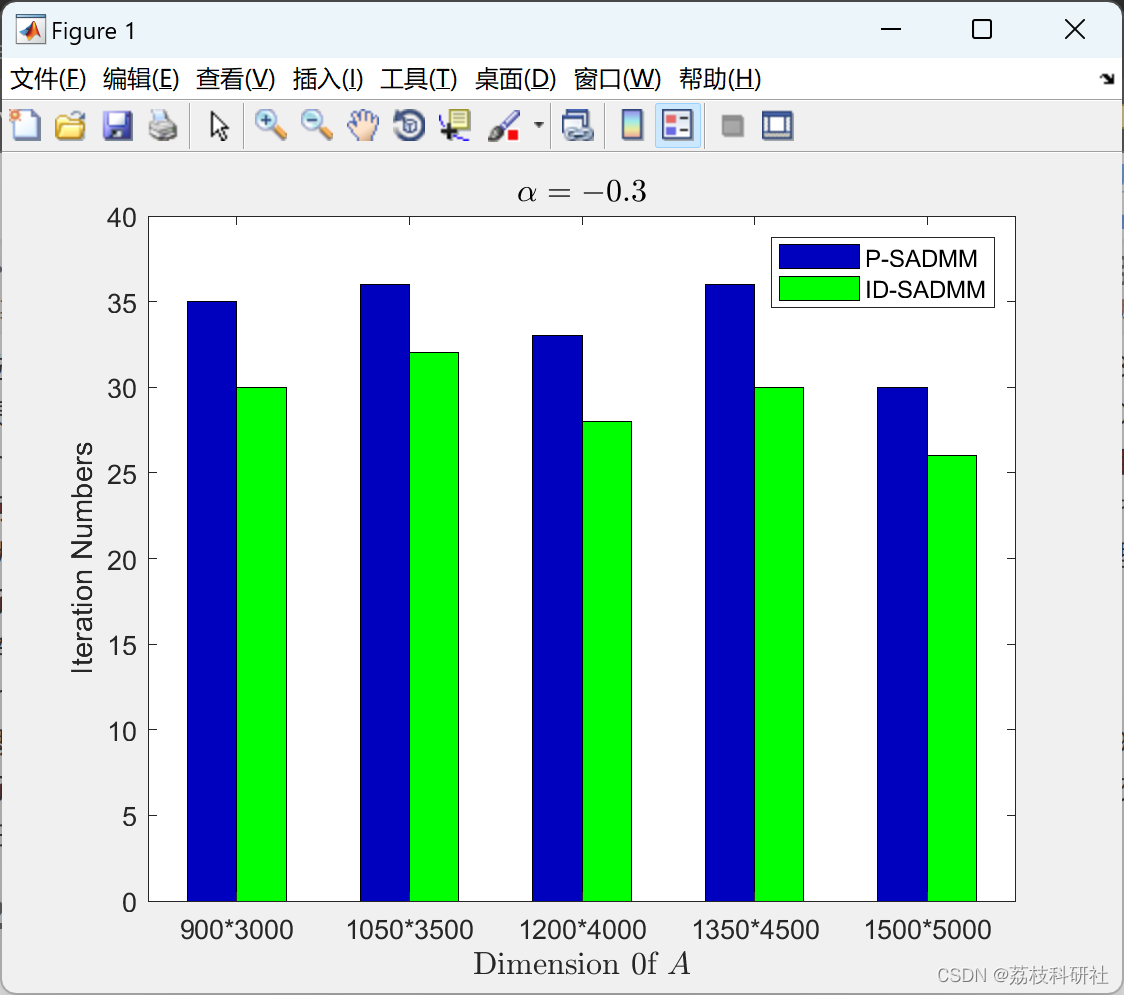



部分代码:
function [x, history] = total_variationILSADMM(b, lambda, rho,r,alpha)
tau=(alpha^2-alpha+4)/(alpha^2-2*alpha+5);
r=r*tau;
% total_variation Solve total variation minimization via ILSADMM
%
% [x, history] = total_variation(b, lambda, rho, alpha)
%
% Solves the following problem via ADMM:
%
% minimize (1/2)||x - b||_2^2 + lambda * sum_i |x_{i+1} - x_i|
%
%OR minimize (1/2)||y - b||_2^2 + lambda * ||Dy||_1
% where b in R^n.
% Let x-Dy=0
% Langrange(x,z)=1/2*|| y - b ||_2^2 + \lambda ||x||_1 - u^T(x-Dy) + rho/2*|| x - Dy ||_2^2
%
% solution of x-subproblem
% x=shrinkage(D*y+u/rho,lambda/rho);
%
% solution of y-subproblem
% y=1/(1+tau*r)*(b+y+1/(tau*r)*q);
% where
% r>rho||A^TA|| and tau\in[0.8,1) and q=-D'*(u-rho*(x-D*y))
%
%updating of multiplier u
%u=u-rho*(x-D*y);
%
% history is a structure that contains the objective value, the primal and
% dual residual norms, and the tolerances for the primal and dual residual
% norms at each iteration.
%
% rho is the augmented Lagrangian parameter.
%
% alpha is the over-relaxation parameter (typical values for alpha are
% between 1.0 and 1.8).
%
%
% More information can be found in the paper linked at:
% http://www.stanford.edu/~boyd/papers/distr_opt_stat_learning_admm.html
%
tau=1;%因为是ADMM,所以tau相当于没有
t_start = tic;
%% Global constants and defaults
QUIET = 0;
MAX_ITER = 1000;
ABSTOL = 1e-4;
RELTOL = 1e-2;
%% Data preprocessing
n = length(b);
% difference matrix
e = ones(n,1);
D = spdiags([e -e], 0:1, n,n);
%% ADMM solver
x = zeros(n,1);
z = zeros(n,1);
u = zeros(n,1);
I = speye(n);
% DtD = D'*D;
for k = 1:MAX_ITER
% x-update
x=shrinkage(D*z+u/rho,lambda/rho);
% u-update
u=u-alpha*rho*(x-D*z);
zold = z;
q=-D' * (u-rho*(x-D*z));
z=1/(1+tau*r)*(b+z+1/(tau*r)*q);
% u-update
u=u-rho*(x-D*z);
% diagnostics, reporting, termination checks
history.objval(k) = objective(b, lambda, x, z);
% history.primalDualError
history.r_norm(k) = norm(x - D*z);
history.s_norm(k) = norm(-rho*D'*(z - zold));
history.eps_pri(k) = sqrt(n)*ABSTOL + RELTOL*max(norm(x), norm(D*z));
history.eps_dual(k)= sqrt(n)*ABSTOL + RELTOL*norm(u);%
if (history.r_norm(k) < history.eps_pri(k) && ...
history.s_norm(k) < history.eps_dual(k))
history.iteration=k;
history.time=toc(t_start);
break;
end
end
% if ~QUIET
% toc(t_start);
% end
end
function obj = objective(b, lambda, x, y)
obj = .5*norm(y - b)^2 + lambda*norm(x,1);
end
function y = shrinkage(a, kappa)
y = max(0, a-kappa) - max(0, -a-kappa);
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]李田雨. 求解正则化逻辑回归问题的非精确ADMM算法[D].北京工业大学,2021.DOI:10.26935/d.cnki.gbjgu.2021.000546.
[2]王冠鹏,田万,胡涛.基于ADMM正则化轨道算法的高维稀疏精度矩阵估计[J].系统科学与数学,2021,41(02):557-565.























 683
683

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








