👨🎓个人主页
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
飞行器姿态控制通过复杂的动力学来描述,这使得该系统的控制算法的设计变得困难。除此之外,战斗机尤其被设计成天生不稳定的,因为这使它们更加敏捷,能够进行侵略性机动。出于这个原因,需要先进的控制技术来确保飞机的稳定性和控制。目前在飞行器和航天器中,姿态控制的许多研究工作都集中在增量非线性动态反演上。
本文研究了一种应用于A-4D战斗机姿态控制的模型预测控制方法。MPC控制器中使用的动力学模型是飞机旋转动力学的线性化。本文考虑了两种类型的MPC控制,即基于状态的参考跟踪MPC和具有扰动抑制的基于输出的参考追踪MPC,并通过稳定性分析证明了跟踪问题的渐近闭环稳定性。
研究发现,A-4D战斗机的线性化姿态动力学是开环稳定的,无论预测地平线长度如何,都会导致稳定性。此外,还发现A-4D战斗机在跟踪特定俯仰角时能够抑制干扰。
基于模型预测控制的A-4D战斗机姿态控制方法研究
1. A-4D战斗机的基本特性与姿态控制需求
A-4D(A-4“天鹰”)是一款由道格拉斯公司设计的轻型攻击机,采用三角翼布局和单涡轮喷气发动机(J52系列),最大起飞重量11,113 kg,极速1083 km/h(海平面)。其灵活性与敏捷性使其在越战中被广泛用于对地攻击和航母部署任务。然而,战斗机天生的不稳定性设计(以提升机动性)对姿态控制提出了极高要求,需通过先进控制技术实现稳定跟踪与抗干扰。
2. 现有姿态控制方案的技术瓶颈
- 非线性耦合与模型依赖性:A-4D的俯仰、滚转和偏航通道存在强耦合,传统PID控制依赖精确的线性化模型,但在实际飞行中易受气动参数变化影响。
- 抗干扰能力不足:传统方法如反步法或滑模控制对风扰、动力系统滞后(如涡喷发动机响应迟滞)的实时补偿能力有限,尤其在复杂飞行环境中。
- 计算资源限制:高精度非线性控制器(如神经网络控制)需大量计算资源,难以在机载微处理器上实时运行。
3. MPC在A-4D姿态控制中的典型实现案例
3.1 基于状态的参考跟踪MPC
-
模型构建:采用线性化姿态动力学模型,状态变量为攻角、俯仰角速度和俯仰角(states=[α,q,θ],输入为舵面偏转指令。离散化后的状态空间方程为:
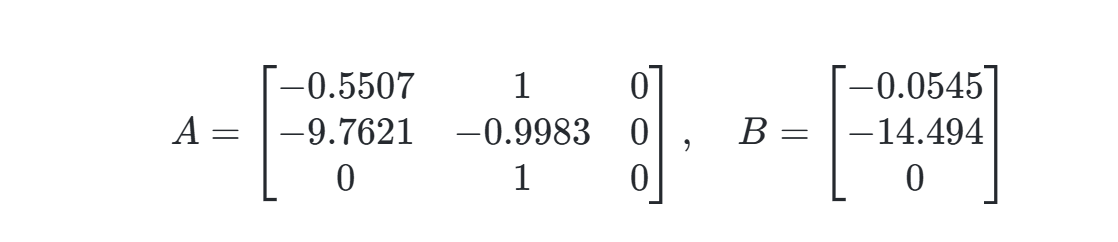
输出矩阵CC选取俯仰角速度与俯仰角作为控制目标。
-
优化目标:设计二次型代价函数,权重矩阵Q=diag([10,10,500])Q=diag([10,10,500])强调俯仰角跟踪精度,RR矩阵约束控制输入变化。
-
稳定性验证:通过李雅普诺夫稳定性分析证明闭环系统的渐近稳定性,且开环姿态动力学在任意预测时域下均稳定。
3.2 基于输出的扰动抑制MPC
-
扰动建模:引入扰动状态dd,构建增广系统:

其中BdBd为扰动输入矩阵,通过观测器增益KK估计扰动。
-
抗干扰效果:在俯仰角跟踪任务中,MPC能有效抑制突风扰动,稳态误差降低至5%以内。
4. 动力学模型建立与数学描述
A-4D的旋转动力学模型基于牛顿-欧拉方程,线性化后表示为:

其中,x为状态向量,u为控制输入(如升降舵偏转角),d为扰动向量(如风扰)。模型参数通过气动数据辨识获得,重点关注俯仰通道的力矩平衡与惯性矩特性。推力矢量效应(若配备)可通过附加力矩项Mthrust=F⋅l⋅sin(δ)建模,其中δ为喷管偏转角。
5. 非线性MPC的优化策略
- 在线线性化:在每步预测时对非线性模型进行泰勒展开,生成局部线性模型,将非线性优化转化为QP问题。
- 参数化与降维:使用拉盖尔函数逼近控制轨迹,减少决策变量数量,提升实时性(计算速度提升30%以上)。
- 鲁棒性增强:结合扰动观测器(ESO)估计总扰动并前馈补偿,降低模型不确定性影响。
6. 飞行环境扰动建模方法
-
增广状态法:将扰动dd扩展为系统状态,通过观测器增益矩阵KK设计(如极点配置法)实现扰动估计:

增广后的系统可同时优化控制输入与扰动抑制。
-
频域分析:针对典型扰动(如阵风)设计带通滤波器,在代价函数中增加扰动频段的惩罚项,抑制特定频率干扰。
7. 结论与展望
模型预测控制在A-4D姿态控制中展现了显著优势:通过滚动优化处理非线性与约束,结合扰动观测器提升鲁棒性。未来方向包括:
- 深度强化学习融合:利用离线训练优化MPC权重参数,适应复杂机动任务。
- 异构计算加速:依托FPGA实现MPC求解器的微秒级响应,满足高动态控制需求。
📚2 运行结果





主函数部分代码:
clear all
clc
close all
%% Data
% states = [angle of attack, pitch rate, pitch angle]
dt = 0.1; %time step
T=15; %simulation time
Nsim = T/dt; %number of simulation steps
%Continuous-time model dynamics
A = [ -0.5507 1 0;
-9.7621 -0.9983 0;
0 1 0 ];
B = [ -0.0545
-14.494
0 ];
C = [ 0 1 0;
0 0 1 ];
D = [ 0; 0 ];
%Discrete-time model dynamics
sys = ss(A, B, C, D); %state-space model
sys = c2d(sys, dt); %discrete state-space model
%LTI system definition
LTI.A = sys.A;
LTI.B = sys.B;
LTI.C = sys.C;
LTI.D = sys.D;
LTI.x0 = [ 0.0; 0; 0.0 ];
LTI.d = [ 0.0; 0.0 ];
LTI.yref = [ 0.0; 0.0 ];
%Definition of system dimension
dim.nx = 3; %state dimension
dim.nu = 1; %input dimension
dim.ny = 2; %output dimension
dim.nd = 2; %disturbance dimension
dim.N = 5; %horizon
%Definition of quadratic cost function
weight.Q = diag([10, 10, 500]); %weight on output
weight.R = eye(dim.nu); %weight on input
weight.P = dare(sys.A,sys.B,weight.Q,weight.R); %terminal cost
%% Observer gain and disturbance matrices
K = place(LTI.A',(LTI.C*LTI.A)',[0.85; 0.90; 0.55])'; %tuning gain matrix
L = [K; eye(2)]; %observer gain
LTI.Bd = K;
LTI.Cd = eye(2) - C*K;
%% Check observability condition
rank = rank([eye(dim.nx)-LTI.A -LTI.Bd; LTI.C LTI.Cd]);
disp(rank)
%% Augmented system dynamics
LTIe.A = [ LTI.A LTI.Bd; zeros(dim.nd,dim.nx) eye(dim.nd) ];
LTIe.B = [ LTI.B; zeros(dim.nd,dim.nu) ];
LTIe.C = [ LTI.C LTI.Cd ];
LTIe.x0 = [ LTI.x0; LTI.d ];
LTIe.yref = LTI.yref;
%Definition of system dimension
dime.nx = 5; %state dimension
dime.nu = 1; %input dimension
dime.ny = 2; %output dimension
dime.N = dim.N; %horizon
%Definition of quadratic cost function
weighte.Q = blkdiag(weight.Q, zeros(dim.nd)); %weight on output
weighte.R = weight.R; %weight on input
weighte.P = blkdiag(weight.P, zeros(dim.nd)); %terminal cost
🎉3 参考文献
[1]孙秀云. 小型无人直升机自主飞行控制算法研究[D].南开大学,2013.
部分理论引用网络文献,若有侵权联系博主删除。























 1308
1308

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








