【HUST】信道编码｜翻译《An LDPC Code Based Physical Layer Message Authentication Scheme With Prefect Security》

写在最前

《An LDPC Code Based Physical Layer Message Authentication Scheme With Prefect Security》 是物理层安全编码中基于LDPC码的一篇论文，其标题的中文翻译很直白，就是《一种基于 LDPC 码的具有完美安全性能的物理层消息安全认证方案》，美中不足的就是论文原文的标题单词打错了，Perfect 打成了 Prefect ……不过也不排除是我孤陋寡闻）。

• 我为什么要翻译它？
  因为我选了《信道编码》，这篇论文是老师给出的LDPC码中影响因子最高的一篇，原文链接。
  
• 为什么我要发出来？
  因为写都写了，和我的研究方向又没啥关系，要是不发出来，估计下一秒我再也找不到它了。
• 我咋翻译的？
  我的研究方向和这个实在没关系，我实在是中文都不一定看得懂，所以我采用了大量的翻译软件。小绿鲸、DeepL、ChatGPT、Kimi 一大堆都用了一遍。
• 看完这篇论文我有什么收获吗？
  我收获了一个宝藏翻译插件，虽然我并不是用它完成的翻译，有兴趣可看：【工具】浏览器插件｜沉浸式翻译，巨巨巨巨巨巨巨好用的浏览器翻译插件！！。

一种基于 LDPC 码的具有完美安全性能的物理层消息安全认证方案

摘要

在本文中，我们研究了无线网络的物理层消息认证，无论对手的计算能力如何，都能实现完美的安全性。具体而言，我们提出了一种基于低密度奇偶校验(LDPC)码和 ϵ-AU₂ 哈希函数的高效可行的认证方案，适用于二进制输入窃听信道。首先，利用新颖的 ϵ-AU₂ 哈希函数族和大环 LDPC 码的对偶，提出了一个针对无噪声主信道情况的多消息认证方案。具体而言，发送方 Alice 首先利用轻量级 ϵ-AU₂ 哈希函数使用消息 M 和密钥 K 生成消息标签 T；然后 Alice 将 T 编码为大环 LDPC 码的对偶的码字 Xⁿ；最后，Alice 将（M，Xⁿ）无噪声地发送给接收方 Bob。攻击者 Eve 具有无限的计算能力，他可以获得消息 M 和输入为 Xⁿ的 BEC 的输出 Zⁿ。然后，进一步开发了一个针对二元擦除信道和二进制输入窃听信道的认证方案，通过利用公开讨论，将嘈杂的主信道情况降低到无噪声主信道情况。我们在理论上证明，如果 Eve 的攻击次数受到关于 n 的多项式上界的限制，所提出的方案是完全安全的。此外，提供了模拟结果，证明了所提出的方案可以在低时间延迟下实现高认证率。

关键词——物理层安全，消息认证，二进制输入窃听信道，LDPC 码。

I. 引言

由于无线介质的广播特性，无线通信系统（例如，5G 网络、车辆通信网络和电子健康系统，如文献[1]和[2]中讨论的，面临几个严重的安全问题[3]，包括修改攻击、替换攻击和重放攻击。对于无线系统来说，提供数据完整性和高级别的安全性是核心要求，这保证了数据在传输过程中没有被更改，并且来自声明的发送者。文献[4]中提出的消息认证技术是确保数据完整性和识别的典型方法。在密码系统中，通常采用基于公钥基础设施（PKI）的数字签名认证进行消息认证。

然而，这些传统的基于密码的消息认证方案有几个局限性：1）由于无线网络（例如，车联网和大量物联网）的动态拓扑结构以及能量受限的终端设备（例如，传感器和移动电话），在无线网络中频繁的密钥分发是有问题的；2）基于 PKI 的方案严重依赖于某些数学问题的计算难度和对手具有有限计算能力的条件。随着对手计算能力的不断提高，这些系统变得脆弱。文献[5]中提出的具有完美安全性（或信息论安全性/无条件安全性）的多消息认证可以解决这些问题。然而，在无噪声信道模型上执行多消息认证时，如文献[4]中推导的，文献[5]证明在 l 次认证后成功攻击的概率至少为 $2^{-H(K)/(\ell +1)}$，随着 l 的增加，这个概率迅速接近 1。

利用物理层（PHY 层）基于秘密密钥的多消息认证可以通过探索底层的特性，例如信道、信号和硬件，实现完美安全性，如文献[9]中讨论的。它可以在对手拥有无限能力的情况下提供安全性，并且不需要频繁的密钥交换。实际上，大量的研究工作已经投入到使用物理层技术实现具有完美安全性的多消息认证上，如文献[10]、[11]、[29]和[30]中提出的。然而，大多数现有工作仍然集中在使用随机编码技术的理论研究上，迫切需要基于具有低复杂度编码和解码算法的编码方案的高效和可行的认证解决方案。

在本文中，我们研究了消息认证，其中 Alice 向 Bob 发送多个消息，同时存在对手 Eve。我们的目标是通过使用轻量级 ϵ-AU₂ 哈希函数和低密度奇偶校验（LDPC）码[12]，以实现相同的密钥 K 在二进制输入窃听信道（BIWC）模型上的完美安全性。实际上，LDPC 码已经被许多无线系统采用，特别是对于 5G 系统，如文献[13]中讨论的。这样，所提出的认证方案更适合 5G。我们考虑二进制输入窃听信道（BIWC）模型，因为它是一个非常通用的模型，许多实际的窃听场景，如二进制擦除窃听信道（BEWC）、二进制对称窃听信道（BSWC）和二进制输入高斯窃听信道（BIGWC）都属于这样的信道模型（详情请参见第 III 节）。

我们首先研究无噪声主信道情况下的多消息认证，其中窃听者的信道是二进制擦除信道（BEC）。考虑到 Eve 具有无限的计算能力，并且可以接收（M，Zⁿ），其中 M 是 Alice 向 Bob 发送的消息，Zⁿ 是给定输入 Xⁿ 的从 Alice 到 Eve 的 BEC 的输出。Eve 的目标是伪造一条消息 $\hat{M}$ 和一个代码 ${\hat{X}}^n$，如果 Bob 接受 $\hat{M}$ 作为有效消息，那么他是成功的。提出了如下的多消息方案。1）Alice 使用 ϵ-AU₂ 哈希函数和高效率生成消息标签 T 和 M 及 K；2）利用大回环 LDPC 码将 T 编码为 Xⁿ；3）通过无噪声信道传输（M，Xⁿ）给 Bob。接收到（M，Xⁿ）后，Bob 通过检查（M，Xⁿ）的一致性来决定拒绝或接受认证。讨论了所提出方案实现完美安全性的条件/要求。理论结果表明，为了实现完美安全性，该方案中使用的哈希函数族和 LDPC 码应满足某些要求（请参见第 V-B 节）。

基于上述结果，我们进一步研究了嘈杂主信道情况下的多消息认证，其中主信道和窃听者的信道都是 BECs。通过使用公开讨论，提出了这种情形下的一种新颖解决方案。主要思想是将嘈杂的主信道情况通过无噪声但不安全校验的信道上的信息交互（即公开讨论）简化为无噪声主信道情况。对于二进制擦除信道和二进制输入窃听者的信道的认证，可以通过使用随机降级信道技术（请参见第 VI 节）从上述方法中推广。

对于所提出方案的实现，提出了一种轻量级 ϵ-AU₂ 哈希函数算法，该算法使用有限域 G(2θ)中的快速乘法算法。此外，还讨论了大回环 LDPC 码序列的构造，以满足所提出方案的要求。理论分析表明，如果 Alice 认证多项式数量的消息，Eve 以 n 的多项式倍数攻击，那么所提出的方案是完美安全的。此外，模拟结果表明，所提出的方案可以实现低时间成本和高认证率。据我们所知，这项工作是第一次通过利用轻量级 ϵ-AU₂ 哈希函数族和大回环 LDPC 码实现具有完美安全性的消息认证。

本文的其余部分组织如下。第 II 节回顾了相关工作。第 III 节介绍了本文中将使用的基本概念和初步知识。第 IV 节介绍了认证模型和对手模型。第 V 节，我们提出了无噪声主信道情况下的认证方案。我们在第 VI 节提出了嘈杂主信道情况下的认证方案。第 VII 节讨论了 ϵ-AU₂ 哈希构造和大回环 LDPC 码设计。第 VIII 节提供了实验结果。第 IX 节提供了结论性评论。

II. 相关工作

A. LDPC 码用于物理层安全

物理层安全[5]-[8]已成为通过利用无线信道的特性、安全信道编码等提高无线通信安全性的新兴技术。相关研究可以追溯到 Wyner 关于窃听信道模型的工作[6]，该工作证明了当窃听信道是主信道的降级版本时，可以实现完美安全性。后来，Csiszár 和 Köner[7] 使用随机编码技术推广了 Wyner 的结果，在这种情况下，窃听信道不必是主信道的降级版本。从那时起，大量关于不同窃听信道模型下的秘密容量的理论研究已经进行[14]、[15]。

基于上述结果，提出了实现安全传输的编码方法[18]-[23]。Ozarow 和 Wyner[18]提出了为修改后的窃听信道构建代码的条件。作为开创性的工作，Thangaraj 等人[19]提出了一种使用 LDPC 码的对偶来实现二进制擦除窃听信道（BEWC）上的弱保密的共集编码方案。Suresh 等人[20]利用无短循环的 LDPC 码的对偶来实现 BEWC 上的强保密。[21]中提出了一种使用大回环 LDPC 码的二进制擦除窃听信道模型的强保密编码方案。[22]中为多个输入多个输出（MIMO）衰落认知多接入窃听信道提出了一种线性预编码器，以最大化平均保密总速率。此外，[23]中讨论了有限字母信号的低复杂度 MIMO 预编码。Polar 码方法用于窃听信道的研究[24]和[25]。[24]中提出了一种对于一般降级和对称窃听信道可实现秘密容量的 Polar 码方法。在[25]中，另一种使用 Polar 码的信道编码方案被提出，用于二进制对称窃听信道模型。

与上述关于安全容量的工作不同，在本文中，我们考虑了在具有完美安全性的窃听信道上进行消息认证的编码方法。使用安全 Polar 码的消息认证已在[31]中讨论。然而，如[21]中提到的，LDPC 码的阈值现象在短于极化的情况下观察到。因此，有足够的兴趣研究使用 LDPC 码进行消息认证。

B. 物理层消息认证

尽管物理层安全传输已经被广泛研究[14]-[17]，但对其姊妹领域物理层消息认证的关注还远远不够。Simmons 的工作[4]在无噪声信道上介绍了一个认证模型。在[26]-[30]中研究了有噪声信道模型上的消息认证。Korzhik 等人[26]讨论了在有（无噪声）公共讨论信道的噪声源模型上的认证。最近，Baracca 等人[27]和 Ferrante 等人[28]研究了在 MIMO 衰落窃听信道上的消息认证。最近，Jiang[29]、[30]考虑了在噪声信道模型上的无密钥认证问题。Lai 等人[10]研究了多消息认证，以实现在窃听信道上的完美安全性。Lai 方法的认证率可以由 Alice 到对手的信道容量界定。然而，这些工作基于随机编码技术，并且认证效率低。因此，这种工作在实践中不能有效实现。最近，Liu 等人[32]和 Ren 等人[33]通过使用信道状态信息提出了一种物理层认证机制。然而，所提出的方案不能提供完美安全性。

与现有工作不同，本文专注于设计实用的多消息认证方案，在 LDPC 码的协助下，在窃听信道上实现完美安全性。具体来说，我们将轻量级 ϵ-AU₂ 类哈希函数和大回环 LDPC 码集成到认证方案中，以实现完美安全性。

III. 初步知识

A. 概念

随机变量（RVs）用 X、Y、…表示，它们的实现用 x、y、…表示，它们的域用 X、Y、…表示。RVs X 和 X’ 在 X 上的对称距离是 $SD(X;X^{\prime })={\sum }_{x\in X}|P_X(x)-P_{X\prime }(x)|$。给定 Y 下 X 和 X’的条件下的距离定义为
$$SD(X|Y;X)=\sum _{y\in Y}P(y)\sum _{x\in X}|P(x|y)-P(x)|\text{\hspace{1em}(1)}$$
函数 negl(n) 在 n 上是可忽略的，如果对于任何多项式 poly(n)，$li{m}_{n\to \infty }negl(n)poly(n)=0$。对于任何正整数 n，[n]表示集合{1, 2, …, n}。|·|是集合的基数，⌊·⌋是向下取整函数。⊕和⊙分别是两个矩阵在有限域 GF(2)上的加法和乘法运算。对于任何矩阵 $A_{n\times r}$ 和 $B_{m\times r}$，矩阵 $A_{n\times r}^T$ 表示 $A_{n\times r}$ 的转置，并且
$$\left[A_{n\times r};B_{m\times r}\right]=\left[\begin{array}{c}{A}_{n\times r}\\ B_{m\times r}\end{array}\right]\text{\hspace{1em}(2)}$$
定义 1: 给定两个有限集合 M = {0, 1}ᵘ 和 T = {0, 1}ᵛ，一个函数族ₖ{φₖ : M → T}_{k∈K} 是 ϵ-almost strongly universal (简记为 ϵ-ASU₂)的，如果：(1) 对于任何 m ∈ M 和 t ∈ T，$P{r}_K({\phi }_k(m)=t)=\frac{1}{|T|}$；以及 (2) 对于任何不同的 m₁, m₂ ∈ M，以及任何 t₁, t₂ ∈ T，$P{r}_K({\phi }_k(m_1)=t_1,{\phi }_k(m_2)=t_2)\le \frac{ϵ}{|T|}$ 。{φₖ}ₖ是 ϵ-almost universal(简记为 ϵ-AU₂) 的，如果第二个条件被替换为：(3) 对于任何不同的 m₁, m₂ ∈ M，$P{r}_K({\phi }_k(m_1)={\phi }_k(m_2))\le ϵ$。

离散无记忆二进制输入信道（即 BIC）定义为一个随机矩阵 W = {W(y|x) : x ∈ {0, 1}, y ∈ Y}。信道 W 被称为二进制擦除信道，擦除概率为 ϵ，简称 BEC(ϵ)。信道 W 被称为二进制对称信道，交叉概率为 ϵ，简称 BSC(ϵ)。具有二进制输入 {-1, +1} 和噪声方差 σ² 的高斯信道被称为二进制输入高斯信道，简称 BIGC(0, δ²)。一个离散无记忆二进制输入窃听信道，简称 BIWC，由两个 BICs W₁ : X → Y 和 W₂ : X → Z 定义，其中 X = {0, 1}是发送方 Alice 的输入字母表，Y 是合法接收方 Bob 的输出字母表，Z 是窃听者 Eve 的输出字母表。

B. LDPC 码

低密度奇偶校验（LDPC）码是具有至少一个备用奇偶校验矩阵的线性码。设 C(λ(x), ρ(x))是 LDPC 码集合，Cⁿ(λ(x), ρ(x))是具有 n 个变量节点的 LDPC 码集合，其中 $\lambda (x)={\sum }_{i\ge 1}{\lambda }_i{x}^i$ 是左边度分布，$\rho (x)={\sum }_{i\ge 1}{\rho }_i{x}^i$ 是右边度分布。度分布 λ(x)和 ρ(x) 是从边的视角来看的，即 λᵢ（ρᵢ）是连接到度为 i 的变量（校验）节点的边的比例。换句话说，λᵢ（resp. ρᵢ）是从一个图中随机均匀选择的边连接到度为 i 的变量节点（resp. 校验节点）的概率。

如果每个变量节点和校验节点具有相同的度 dᵥ 和 $d_c$，即 $\lambda (x)=x^{(}{d}_v-1)$ 和 $\rho (x)=x^{(}{d}_c-1)$，那么在集合 $Cn(x^{(}{d}_v-1),x^{(}{d}_c-1))$ 中的码（简称为 C(n, dᵥ, $d_c$)）被称为规则 LDPC 码。每个 LDPC 码都可以对应一个二分图，称为 Tanner 图[34, 第 2.4 节]，如下所示。设 C 是 LDPC 码，H 是 C 的奇偶校验矩阵，其尺寸为 m × n。C 的 Tanner 图是图 G(P, E)，其中节点集 P = {c₁, ···, cₘ} ∪ {v₁, ···, vₙ}和边集 E = {(cᵢ, vⱼ)|if Hᵢⱼ = 1}，其中 cᵢ 是校验节点，vⱼ 是变量节点，对于任何 i ∈ {1, 2, ···, m} 和 j ∈ {1, 2, ···, n}。具有 n 个变量节点的 Tanner 图表示为 G(n, P, E)。图的回环长度是图中包含的最短循环的长度。

定义 2: 一个 Tanner 图序列{G(n, P, E)}ₙ 是大回环的，如果其回环长度随着 log n 的增加而增加。一个 LDPC 码序列被称为大回环 LDPC 码，如果它们对应的 Tanner 图序列是大回环的。

IV. 无线窃听信道上的消息认证

在本节中，首先介绍认证模型，然后是对手模型和安全认证方案的定义。

A. 认证模型

假设发送方 Alice 希望在对手 Eve 的参与下，传输并认证多个消息给接收方 Bob。如图 1 所示，存在一个从 Alice 到 Bob 的具有擦除概率 ${\xi }_m$ 的 BEC W₁ : X → Y，记为 BEC(${\xi }_m$)，以及一个从 Alice 到 Eve 的 BIC W₂ : X → Z。

为了防止 Eve 的攻击，Alice 和 Bob 在消息认证之前共享了一个秘密密钥 K。请注意，关于在嘈杂信道上进行密钥生成的问题，已经从理论和实施的角度进行了广泛研究，例如[36]和[35]。可以使用这些密钥生成方案获得认证密钥。

如图 2 所示，如果 Alice 希望认证消息 M，Alice 首先使用输入 K、M 和一个随机性 R 生成消息认证码（MAC）Xⁿ，即 Xⁿ = f(M, K, R)，其中 f 是编码函数；然后，Alice 将 M 和一个纠错码通过窃听信道（W₁, W₂）发送；最后，Alice 将 Xⁿ 通过(W₁, W₂)传输给 Bob。接收到(M, Yn)后，Bob 使用验证函数 g 计算 V er = g(M, K, Yn)，其中 V er ∈ {⊥, ⊤}。如果 V er = ⊤，Bob 接受 M 并给 Alice 发送决策位 1；否则，他拒绝它并给 Alice 发送决策位 0。假设 Eve 可以解码 M，并且可以查看 W₂ 的输出 Zⁿ。

B. 对手模型

在本文中，对手模型如下所示。(1) Eve 的计算能力被认为是无限的。Eve 知道整个认证方案和参数的值，除了 Alice 和 Bob 共享的秘密密钥；(2) Eve 被允许查看信道 W₂ : X → Z 的输出，以了解 Alice 认证的消息，并了解每次认证的决策位；(3) 存在一个从 Eve 到 Bob 的无噪声信道，Eve 可以无噪声地向 Bob 发送任何信息。这样的假设为对手提供了更多的优势。Eve 的目标是伪造一条消息 $\hat{M}$ 和一个 MAC ${\hat{Y}}^n$，使得当 Bob 接收到($\hat{M}$, ${\hat{Y}}^n$)时，他接受 $\hat{M}$ 作为合法消息。

我们希望确保即使 Eve 自适应地攻击了 n 的多项式次，他仍然不能欺骗 Bob 接受一个虚假的认证。正式的攻击模型（包括类型 I 和类型 II 攻击）如下。让 Mᵢ（i = 1, 2, …）是 Alice 认证的消息序列，$X_i^n$ 是 Mᵢ 的码字。根据对手模型，Eve 可以接收到消息 Mᵢ 和 W₂ 的输出 Zⁿ i，即 Eve 也可以了解决策位 bi。

类型 I：Eve 可以通过在 Alice 发送(Mᵢ, $X_i^n$ )给 Bob 时，用 M’ᵢ 替换 Mᵢ 来发动攻击。这里，伪造的消息 M’ᵢ 是基于 Mᵢ、Eve 的本地随机源 R 以及之前收集的信息：{(Mⱼ, $Z_j^n$)}${}_{j=1}^{i-1}$ 和决策位{bⱼ}${}_{j=1}^{i-1}$ 第一阶段的信息；以及第二阶段的{(${\hat{M}}_t$, ${\widehat{Z^n}}_t$)}ₜ 和决策位{${\hat{b}}_t$}ₜ。

类型 II：Eve 可以自适应地向 Bob 无噪声地发送(${\hat{M}}_t$, ${\hat{X}}_t^n$)。Eve 将了解 Bob 的决策位 ${\hat{b}}_t$。这里(${\hat{M}}_t$, ${\hat{X}}_t^n$)是根据 R 和之前收集的信息：第一阶段的{(Mⱼ, $Z_j^n$, bⱼ)}ⱼ 和第二阶段的{(${\hat{M}}_j$, ${\widehat{Z^n}}_j$),${\hat{b}}_j$}${}_{j=1}^{t-1}$ 发送的。

在这个模型中，我们允许 Eve 任意交错类型 I 攻击和类型 II 攻击。我们使用 succ 表示 Eve 成功进行类型 I 或类型 II 攻击的事件。考虑 Eve 可以了解验证结果的模型已经在[41]中考虑过。这是实际的，因为接收方在拒绝或接受后的行动可能是可见的。

C. 安全认证方案

如果一个密码方案即使在对手拥有无限计算能力的情况下也无法被破解，则该密码方案是完美安全的。在本文的其余部分，除非另有说明，“安全”意味着“完美安全”。

定义 3: 对于一个窃听信道 W₁ : X → Y, W₂ : X → Z 的密码方案 Πₙ 是安全认证方案，如果满足以下条件（保持模型中的概念）。

1. 完备性：当窃听者 Eve 不出现时，存在 α > 0，使得 Pr(D = ⊥) ≤ exp(-nα)，其中 n 是窃听信道(W₁, W₂)的使用次数。
2. 认证性：对于任何窃听者 Eve，成功概率 Pr(Succ(Eve))在 n 的多项式倍数攻击后是可忽略的。除了安全性要求，我们还定义认证率为效率指标。认证率 ${\rho }_{auth}$ 是源消息长度与码字长度的比率，即 ${\rho }_{auth}$ = $\frac{1}{n}$ * log|M|，其中 |M| 是消息空间 M 的基数。

V. 无噪声主信道情况下的认证

在本节中，我们研究了主信道无噪声的无线窃听信道模型上的认证。首先，我们为二进制擦除窃听者的信道提出了一种新的认证方案。然后，讨论了所提出方案实现完美安全性的要求。

A. 无噪声主信道情况下的认证

我们考虑在主信道无噪声且窃听信道是二进制擦除信道 BEC(ζ)的情况下的消息认证，其中 ζ 是窃听者信道中的擦除概率。设置：设 Φ = {φₖ}k∈K 是从 M = {0, 1}ᵘ 到 T = {0, 1}ᵛ 的 ϵ-AU₂ 哈希函数集合。设 C 是(n, l)线性码，v ≤ n - l，G 是 C 的生成矩阵，其行是 g1, g2, …, gl。在码 C 的 $2^{(}n-l)$ 个共轭类中，Alice 从{0, 1}ⁿ/C 中选择 v 个线性独立的向量 r1, r2, …, rv，并向 Bob 宣布它们。认证：假设 Alice 和 Bob 共享一个秘密密钥 k ∈ K。如果 Alice 想要认证消息 m ∈ M 到 Bob，他们如下交互：

1. Alice 首先计算 t = φₖ(m) = [t₁, t₂, …, tᵥ]（称为消息标签），然后，使用以下步骤对 t 进行编码以得到 xⁿ：

   • 随机选择一个向量 s = [s₁, s₂, …, sₗ]在向量空间{0, 1}ˡ 中；
   • 计算 xⁿ 通过
     $$x^n=t\odot [r_1;r_2;...;r_v]\oplus s\odot [g_1;g_2;...;g_l]\text{\hspace{1em}(3)}$$
     最后，Alice 通过窃听信道(W₁, W₂)发送 m 和 Xⁿ。

2. 假设 Bob 接收到 m’和 yⁿ，Eve 分别接收到 m 和 Zⁿ，其中 m’和 yⁿ 的值取决于是否发生了攻击（即，如果没有发生攻击，m’ = m 且 yⁿ 是信道 W₁ 的输出；否则，m’（= m）是 Eve 想发送给 Bob 的伪造消息，yⁿ 可以等于或不等于信道 W₁ 的输出，这取决于对手的策略）。在接收到 m’和 yⁿ 后，Bob 首先计算 t’ = φₖ(m’)，然后验证
   $$a^n\triangleq t^{\prime }\odot [r_1;r_2;...;r_v]\oplus y^n\in C\text{\hspace{1em}(4)}$$
   如果 aⁿ ∈ C，Bob 接受它；否则，他拒绝它。请注意，如果 H 是 C 的奇偶校验矩阵，那么 aⁿ ∈ C 当且仅当 H · $[a^n{]}^T=[0^n{]}^T$，其中[aⁿ] = [a₁, a₂, …, aₙ]。有关使用二进制擦除窃听信道的无噪声主信道情况的提出的方案的详细信息，请参阅算法 1。

---

算法 1 无噪声主信道情况下的认证
加密：如果 Alice 想要认证消息 m，她 1. 计算消息标签 t = φₖ(m) = [t₁, t₂, …, tᵥ]； 2. 随机选择一个向量 s = [s₁, s₂, …, sₗ]在{0, 1}ˡ 中； 3. 通过 Xⁿ = t ⊙ [r₁; r₂; …; rᵥ] ⊕ s ⊙ [g₁; g₂; …; gₗ]计算消息认证码 Xⁿ； 4. 通过窃听信道(W₁, W₂)发送(m, Xⁿ)给 Bob。 验证：在接收到(m’, yⁿ)后，Bob 1. 计算 aₙ = [a1, …, aₙ] = φₖ(m’) ⊙ [r₁; r₂; …; rᵥ] ⊕ yⁿ； 2. 计算 H · $[a_n{]}^T$，并验证 H · $[a_n{]}^T=[0^n{]}^T$； 3. 如果 $H\cdot [a_n{]}^T=[0^n{]}^T$，他接受 m’并向 Alice 发送决策位 1；否则，他拒绝它，并向 Alice 发送 0。

B. 完美安全性的条件

接下来，我们给出了关于算法 1 实现完美安全性的条件的认证定理。

定理 1：给定一个窃听信道(W₁, W₂)，其中无噪声主信道 W₁ 和噪声窃听者的信道 W₂ = BEC(ζ)，设 P(n)_e(ξ)是来自 Cn(λ, ρ)的码在 BEC(ξ)上的块错误概率。如果以下条件成立：

(1) ϵ-AU₂ 哈希函数族{φₖ : M → T}${}_{k\in K}$ 满足 ϵ 和|T|/|K|在 n 上是可忽略的；

(2) 存在 η ∈ [0, 1]，使得对于任何 ξ < η，$P(n{)}_e(\xi )<ex{p}^{(}-\alpha n)$（对于某个常数 α > 0），则在算法 1 中使用的 ϵ-AU₂ 哈希函数和 Cn(λ, ρ)的码的对偶可以在(W₁, W₂)上实现完美保密，对于 ζ > 1 - η。

这个定理的详细证明将在附录 B 中提供。有了这个定理，我们只需要构造一个满足条件(1)的哈希函数族和一个满足条件(2)的 LDPC 码，以确保所提出的认证方案的安全性。我们将在第 VII 节讨论如何设计计算效率高的 ϵ-AU₂ 类哈希函数和 LDPC 码以满足这些要求。

VI. 嘈杂主信道情况下的认证

在本节中，我们研究嘈杂主信道情况下的消息认证。首先，我们提出了一个带有公开讨论的 BEWC 上的新颖认证方案。然后，通过利用随机降级信道技术，提出了一个二进制擦除主信道和二进制输入窃听者的信道上的认证方案。

A. 在 BEWC 上的提出的认证方案

我们首先考虑在 BEWC (W₁, W₂)上的消息认证，其中 W₁ = BEC(${\xi }_m$)且 W₂ = BEC(${\xi }_w$)。在这种情况下，实现完美安全认证的一个直观方法是设计一个具有生成矩阵 G 的 LDPC 码 C，并选择一组向量 r₁, r₂, …, rᵥ 在{0, 1}ⁿ/C 中，具有以下属性：(1) 安全性：C 的对偶在 BEC(${\xi }_w$)上的块错误概率随着 n 呈指数下降；以及(2) 可靠性：G = [G; D]是 LDPC 码 C 的生成矩阵，使得在 BEC(${\xi }_m$)上的块错误概率足够小，其中 D = [r₁; r₂; …; rᵥ]。然而，如[19]中提到的，构造这样的码是困难的。

一个有希望的解决方案是使用公开讨论进行消息认证。如图 3 所示，认证信道模型包括一个窃听信道(BEC(${\xi }_m$), BEC(${\xi }_w$))。此外，为了简化解释，我们假设 Alice 和 Bob 之间有一个不安全且无噪声的公共信道，称为公共信道，该信道完全受到 Eve 的控制。请注意，1) 公共信道可以被视为具有纠错码的噪声信道；以及 2) 由于通过公共信道传输的信息已经使用某种纠错码进行了编码，我们不能保证 Eve 不能解码它。因此，假设公共信道完全受到 Eve 的控制是合理的，甚至加强了 Eve 的能力。

然后，我们提出了一个新颖的认证方案，用于二进制擦除主信道情况。主要思想是通过公开讨论将嘈杂的主信道情况简化为无噪声的主信道情况，如下所示。当 Bob 接收到来自 Alice 的输入 xⁿ 的 BEC(${\xi }_m$)的输出 yⁿ 时，他将擦除位置的索引集 $E{P}_B$（即，$E{P}_B$ = {i : yᵢ =?}）通过无噪声的公共信道发送给 Alice。收到 $E{P}_B$ 后，Alice 通过公共信道将 xⁿ($E{P}_B$) = {xᵢ : i ∈ $E{P}_B$}传输给 Bob。相应地，Bob 在接收到 xⁿ($E{P}_B$)后可以获得 xⁿ。为了安全，我们需要确定在算法 1 中用于生成 xⁿ 的窃听者的信道。根据大数定律，如果 n 足够大，那么擦除位置集 $E{P}_B$ 的基数小于或等于 n(${\xi }_m$ + 1/2σ)，而 $E{P}_E$ 的基数大于 n(${\xi }_w$ - 1/2σ)，其中 σ = σ(n)，当 n 趋向于无穷大时，σ(n)趋向于 0。对于合法用户来说，最坏的情况是 $E{P}_B$ ⊆ $E{P}_E$，这意味着 Eve 可以从 Zⁿ 和 xⁿ($E{P}_B$)中学习到最多的 xᵢ（i = 1, …, n）。因此，我们有
$$|E{P}_E|-|E{P}_B|\ge n({\xi }_w-{\xi }_m-\sigma )\text{\hspace{1em}(5)}$$
对于足够大的 n。在最坏的情况下，即|$E{P}_E$| - |$E{P}_B$| = n(${\xi }_w$ - ${\xi }_m$ - σ)，如果使用算法 1 生成 xⁿ，并将窃听者的信道视为 BEC(${\xi }_w$ - ${\xi }_m$ - σ)，其中 0 < σ < min{${\xi }_w$ - ${\xi }_m$, 1/2${\xi }_w$}，则可以提供安全性。

值得一提的是，在一般情况下，|$E{P}_B$| < n(${\xi }_w$ + 1/2σ)。设 b = ⌊(${\xi }_m$ + 1/2σ)n - |$E{P}_B$|⌋，则在一般情况下 b > 0。基于上述讨论，我们在公开讨论阶段改进了我们的方法，以进一步防止 Eve 篡改响应 xⁿ($E{P}_B$)。具体来说，Bob 首先从[n]/$E{P}_B$ 中随机选择一个索引集 $R{P}_B$ = {j1, …, jb}，并将 $E{P}_B$ ∪ $R{P}_B$（而不是 $E{P}_B$）通过公共信道发送给 Alice。接收到 $E{P}_B$ ∪ $R{P}_B$ 后，Alice 通过公共信道传输 xⁿ($E{P}_B$ ∪ $R{P}_B$)作为响应。由于 Bob 知道 xⁿ($R{P}_B$)，他可以检查响应 xⁿ($E{P}_B$ ∪ $R{P}_B$)是否被篡改。由于 Eve 不能区分 $R{P}_B$ 和 $E{P}_B$ ∪ $R{P}_B$，因此很难伪造一个响应ˆxⁿ($E{P}_B$ ∪ $R{P}_B$)，使得该响应能够通过 Bob 的检查（即，ˆxⁿ($R{P}_B$) = xⁿ($R{P}_B$)）。有关二进制擦除主信道情况下的提出的认证方案的详细信息，请参阅算法 2。

---

算法 2 二进制擦除主信道情况下的认证
1. 假设 BEWC $(W_1,W_2)$ 是一个窃听信道，其中主信道 $W_1=\text{BEC}({\xi }_m)$，窃听者的信道 $W_2=\text{BEC}({\xi }_w)$。 2. Alice 在算法 1 的编码过程中执行步骤 1-3，其中使用的是 BEWC $(W_1^{\prime },W_2^{\prime })$，$W_1^{\prime }$ 是一个无噪声信道，$W_2^{\prime }=\text{BEC}({\xi }_w-{\xi }_m-\sigma )$，其中 $\sigma$ 是一个常数，满足 0 < σ < min ⁡ { ξ w − ξ m , 1 2 ξ w } 0 < \sigma < \min\{\xi_w - \xi_m, \frac{1}{2}\xi_w\} 0<σ<min{ξw​−ξm​,21​ξw​}。 3. Alice 通过窃听信道 $(W_1,W_2)$ 发送 $m$ 和 $x^n$ 给 Bob。 4. 让 $(m,y^n)$ 是 Bob 接收到的信息， E P B = { i : y i = ? } = { i 1 , . . . , i a } EP_B = \{i : y_i = ?\} = \{i_1, ..., i_a\} EPB​={i:yi​=?}={i1​,...,ia​} 是擦除位置。Bob 首先计算 $b=\lfloor ({\xi }_m+\frac{1}{2}\sigma )n-|E{P}_B|\rfloor$。然后，Bob 从 { 1 , . . . , n } / E P B \{1, ..., n\} / EP_B {1,...,n}/EPB​ 中随机选择一个索引集 R P B = { j 1 , . . . , j b } RP_B = \{j_1, ..., j_b\} RPB​={j1​,...,jb​}。最后，Bob 通过公共信道将 $E{P}_B\cup R{P}_B$ 传输给 Alice。 5. Alice 检查 $|E{P}_B\cup R{P}_B|$ 是否小于或等于 $n({\xi }_w+\frac{1}{2}\sigma )$。如果是，Alice 通过公共信道将 $x^n(E{P}_B\cup R{P}_B)$ 发送给 Bob；如果不是，Alice 返回步骤 2。这里的 $x^n(E{P}_B\cup R{P}_B)$ 是对应于索引集 $E{P}_B\cup R{P}_B$ 的 $x^n$ 中的元素。 6. Bob 首先检查 $x^n(R{P}_B)$ 是否等于 $y^n(R{P}_B)$。如果是，Bob 使用 BEWC $(W_1^{\prime },W_2^{\prime })$ 执行算法 1 中的验证过程；如果不是，Bob 拒绝 $m$。

B. 完美安全性的条件

基于上述讨论，我们得到了算法 2 实现完美安全性的条件。定理 2：假设(W₁, W₂)是一个窃听信道，其中 W₁ = BEC(${\xi }_m$)且 W₂ = BEC(${\xi }_w$)，且 ${\xi }_m$ < ${\xi }_w$。如果哈希函数和 LDPC 码的对偶满足定理 1 中的条件(1)和(2)，并且在(W₁, W₂)上使用算法 2，其中 σ 是一个常数，满足 0 < σ < min{${\xi }_w$ - ${\xi }_m$, 1/2${\xi }_w$}，W′1 是一个无噪声信道，W′2 = BEC(${\xi }_w$ - ${\xi }_m$ - σ)。那么，当 n 足够大时，可以为 ζ > 1 - η 提供算法 2 的完美安全性。

这个定理的详细证明将在附录 C 中给出。这个定理表明，通过利用公开讨论方法，可以在二进制擦除窃听信道上实现完美安全认证。为了进一步说明所提出的方案，我们有以下示例。考虑一个 BIWC(W₁, W₂)，其中 W₁ 是 BEC(0.1)，W₂ = BEC(0.617)。取 δ = 0.017，Alice 可以使用 BEWC(W′1, W′2)执行算法 1 来生成一个码字，其中 W′1 是一个无噪声的主信道，W′2 = BEC(0.5)是一个噪声窃听者的信道。然后，Alice 和 Bob 按照算法 2 的步骤 3-6 进行完美安全认证。

为了进一步说明算法 2 的主要思想，我们使用一个简单的例子来展示它的工作原理，而不考虑安全性和认证效率。在这个例子中，使用具有生成矩阵 G 的汉明(15, 4)码，并且从{0, 1}ⁿ/G 中随机选择了线性独立的向量[r₁; …; r₄]。如图 4 所示，Alice 首先计算 t = φₖ(m)（详细信息将在第 VII 节-B 中提供）；然后，计算 x¹⁵ = t ⊙ [r₁; …; r₄] ⊕ s ⊙ G，其中 s 是从{0, 1}^11 中随机选择的。如图 5 所示，当 Alice 通过(BEC(${\xi }_m$), BEC(${\xi }_w$))传输 x¹⁵ 和 m 时，Bob 和 Eve 分别接收到(m′, yⁿ)和(m, Zⁿ)，其中 m′取决于 Eve 的攻击。然后，Bob 检查 y15 的擦除位置 $E{P}_B$ = {3, 4, 13}，并将其通过公共信道发送给 Alice。接下来，Alice 通过公共信道将 x¹⁵($E{P}_B$) = {0, 0, 1}发送给 Bob 作为响应。获得 x¹⁵($E{P}_B$)后，Bob 恢复 x¹⁵ 并计算 $H\odot [y15\oplus {\phi }_k(m\prime ){]}^T$，其中 H 是汉明(15, 4)码的奇偶校验矩阵。如果结果为$[0^n{]}^T$，Bob 接受 m；否则，Bob 拒绝它。同时，Eve 可以恢复擦除位集合 $E{P}_E$ 中的擦除位。

C. 二进制输入窃听者的信道上的认证

现在我们考虑在二进制擦除主信道和二进制输入窃听者的信道上的消息认证。首先，我们引入两个无记忆嘈杂信道之间的基本关系。

定义 4：如果存在一个信道 W3 : Y → Z，使得对于任何(x, z) ∈ X × Z，有 W₁(z|x) = ∑y∈Y W₂(z|y)W3(y|x)，则称信道 W₁ : X → Z 相对于信道 W₂ : X → Y 是随机降级的。根据[37, Prop. 6.4]，任何二进制输入信道都相对于二进制擦除信道是随机降级的。

---

算法 3 二进制擦除主信道和二进制输入窃听者的信道上的认证
1. 给定一个 BIWC (W₁, W3)，其中主信道 W₁ = BEC(${\xi }_m$)，窃听者的信道 W3 是二进制输入信道。 2. 通过计算 ζ 的方程(6)，创建一个二进制擦除信道 W₂ = BEC(${\xi }_w$)，其中方程(6)中的 W 是 W3。 3. 使用 BEWC (W₁, W₂)执行算法 2。

具体来说，如果 W : {0, 1} → Z 是一个二进制输入信道，信道 W 相对于 BEC(${\xi }_w$)是随机降级的其中
ξ w = ∫ z min ⁡ u ∈ { 0 , 1 } W ( z ∣ u ) d z (6) \xi _ { w } = \int _ { z } \min _ { u \in \left\{ 0 , 1 \right\} } W ( z | u ) d z \tag{6} ξw​=∫z​u∈{0,1}min​W(z∣u)dz(6)
认证方案对于二进制擦除主信道和二进制输入窃听者信道（BE-BI 情况）可以通过以下算法（例如，算法 3）获得。

我们推广了在 BEWC 上的提出的认证方案的理论结果到二进制输入窃听者信道情况。

定理 3：假设(W₁, W3)是一个窃听信道，其中 W₁ = BEC(${\xi }_m$)，W3 是二进制输入窃听者信道。假设 W3 相对于擦除信道 W₂ = BEC(${\xi }_w$)是随机降级的。如果在算法 3 中使用的哈希函数和 LDPC 码的对偶满足定理 2 中的条件(1)和(2)，并且用于(W₁, W3)上的算法 3，它可以为 ζ > 1 - η 提供算法 3 的完美安全性。

详细的证明将在附录 D 中提供。这个定理表明，即使在窃听者的信道是 BIC 的情况下，也可以通过使用随机降级信道技术实现完美安全认证。

我们用以下示例来说明这个方案。考虑一个 BIWC(W₁, W3)，其中 W₁ = BEC(${\xi }_m$)，${\xi }_m$ = 0.1，W3 是具有输入{-1, +1}和噪声方差 1 的二进制输入高斯信道。根据方程 6，我们可以创建一个二进制擦除信道 W₂ = BEC(${\xi }_w$)，其中
ξ w = ∫ z min ⁡ u ∈ { − 1 , 1 } W ( z ∣ u ) d z (7) \xi _ { w } = \int _ { z } \min _ { u \in \left\{ - 1 , 1 \right\} } W ( z | u ) d z \tag{7} ξw​=∫z​u∈{−1,1}min​W(z∣u)dz(7)
$$=2{\int }_1^{+\infty }\frac{1}{\sqrt{2\pi }}{e}^{-\frac{x^2}{2}}dx=0.317\text{\hspace{1em}(8)}$$

因此，Alice 和 Bob 可以使用 BEWC(W₁, W₂)执行算法 2 来实现安全认证。

VII. 提出方案的实现

在本节中，我们讨论了所提出认证方案的实现。关键步骤是设计一个计算效率高的 ϵ-AU₂ 类哈希函数和一系列大回环规则 LDPC 码，以满足秘密定理（即，定理 1、2 和 3）的安全要求。

A. 有限域 GF($2^{\theta }$)的生成

对于实现，有必要提出一个 ϵ-AU₂ 哈希方案，以满足定理 1 的要求，并具有高计算效率。第一步是生成一个有限域 GF($2^{\theta }$)。让 θ 是多项式
$$\Psi (x)=x^{\theta }+x^{(}\theta -1)+...+x+1\text{\hspace{1em}(9)}$$

的度数，具有以下属性：(1) θ + 1 是素数；以及(2) 2 是模 θ + 1 的原根，即，对于任何素数 p 整除 θ，有 $2^{\theta /p}$ ≢ 1 mod (θ + 1)。如[40]中提到的，有许多正整数满足这些属性，其中一些在表 1 中给出。

从有限域理论的基本知识中，Ψ(x)在 GF(2)[x]中是不可约的，并且商环 GF(2)[x]/(Ψ(x))可以用来描述 GF($2^{\theta }$)，其中 GF(2)[x]是 GF(2)上的多项式环，(Ψ(x))是由 Ψ(x)生成的 GF(2)[x]的理想。在这种情况下，GF($2^{\theta }$)中的任何元素(α0, …, α^(θ-1))可以表示为 $\alpha (x)\triangleq \alpha 0+\alpha 1x+...+{\alpha }^{(}\theta -1)x^{(}\theta -1)$。

B. 轻量级 ϵ-AU₂ 方案

在[39]中，den Boer 提出了一个哈希函数族，如下所示。

定义 5：设 $q$ 是一个素数幂，$\tau$ 是一个正整数，$GF(q)$ 是一个有限域。设 $M=(GF(q){)}^{\tau }$，$K=(GF(q){)}^2$，$T=GF(q)$。对于任何密钥 $k=(k_0,k_1)\in K$，其中 $k_0,k_1\in GF(q)$，定义 ${\varphi }_k:M\to T$ 为
$${\varphi }_k(a_1,\cdots ,a_{\tau })=k_0+a_1{k}_1+\cdots +a_{\tau }{k}_1^{\tau }\text{\hspace{1em}(10)}$$
对于每个 $(a_1,...,a_{\tau })\in M$。

根据[39]，哈希族 { ϕ k } k \{\phi_k\}_k {ϕk​}k​ 是 $ϵ$-AU${}_2$ 的，其中 $|M|=q^{\tau }$，$|K|=q^2$，$|T|=q$，并且 $ϵ=\tau /q$。显然，通过取 $q=2^{\theta }$ 和 $\tau =\text{poly}(\theta )$，由定义 5 构造的 $\text{poly}(\theta )/2^{\theta }$-AU${}_2$（以及 $\text{poly}(\theta )/2^{\theta }$-AU${}_2$）类哈希函数满足定理 1 的要求。

为了有效地进行哈希计算，我们需要考虑 $GF(2^{\theta })$ 中乘法的轻量级算法。幸运的是，Silverman 提出了一个在 $GF(2^{\theta })$ 中进行乘法的算法，其复杂度为 $\theta +1$ [40]。为了方便，Silverman 乘法算法执行的操作用 Mul(·)表示。

基于上述讨论，我们提出了一个轻量级哈希算法，如下所示：

1. 我们选择一个正整数 $\theta$，并使用第 VII-A 节中的方法生成一个有限域 $GF(2^{\theta })$；选择两个正整数 ${\tau }_0$ 和 $\tau$，使得 $\tau =\text{poly}(\theta )$ 对于一个多项式函数 $\text{poly}(\cdot )$，并且 $\tau$ 可以被 ${\tau }_0$ 整除（记为 $\pi =\tau /{\tau }_0$）。
2. 如果 $(k_0,k_1)$ 是安全密钥，我们预先计算 ${\tau }_0$-向量 $[k_1^1,k_2^1,...,k_{{\tau }_0}^1]$，$\pi$-向量 $[k_{{\tau }_0}^1,k_{2{\tau }_0}^1,...,k_{\pi {\tau }_0}^1]$，然后保存它们。
3. 对于任何 $m=(a_1,...,a_{\tau })$，我们可以通过
   $${\varphi }_k(m)=k_0+\sum _{i=0}^{\pi -1}{k}_1^{i{\tau }_0}\sum _{j=1}^{{\tau }_0}{a}_{i{\tau }_0+j}{k}_1^j\text{\hspace{1em}(11)}$$
   计算 ${\varphi }_k(m)$。

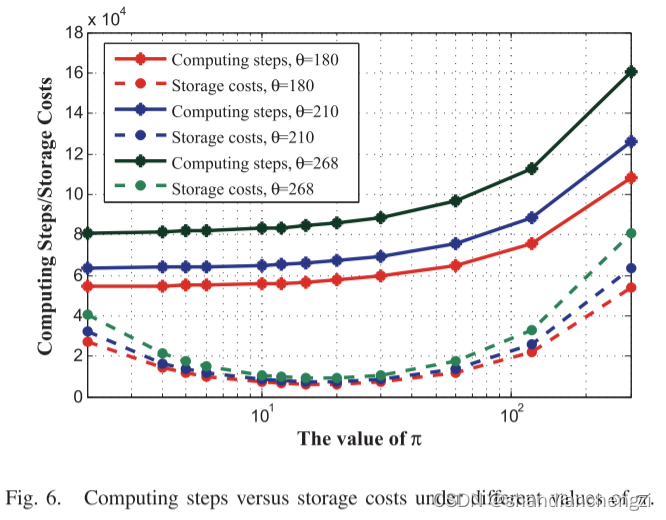
图 6 显示了在不同 π 值下，计算步骤与存储成本的关系。例如，如果 θ = 268，τ = 300，τ0 = 15，消息长度约为 80KB，密钥长度为 536 位，标签长度为 268 位， ϵ ≈ $2^{-260}$，计算步骤的数量约为 $8.4\times 10^4$，存储成本约为 9 KB。然而，如果 θ = 268，τ = 300，τ0 = 50，计算步骤的数量约为 $7.3\times 10^4$，存储成本约为 15 KB。

C. 大回环规则 LDPC 码的构造

我们展示了如何找到一个大回环规则 LDPC 码以满足所提出认证方案的安全要求。根据[34, 第 2.5 节]，C(n, dᵥ, $d_c$)的设计速率可以表示为
$$r(n,d_v,d_c)=1-\frac{{\int }_0^1\rho (x)}{{\int }_0^1\lambda (x)}=1-\frac{d_c}{d_v}\text{\hspace{1em}(12)}$$

由于任何实数 r 在[0, 1]内都可以通过 1 - $d_c$/dᵥ 无限逼近，其中 $d_c$ 和 dᵥ 可以是任何正整数。我们只需要利用规则 LDPC 码实现所提出的方案，以满足不同窃听者信道中的码率要求。这里，我们采用了大回环规则 LDPC 码的编码方案，该方案可以在二进制擦除信道上实现块错误概率双指数下降[21]。有关编码方案的详细信息，请参见[21]。根据[21, Th. 9]，我们有以下结果。定理 4：让{Cn}n 是使用[21, 算法 4]的大回环(dᵥ, $d_c$)-规则 LDPC 码序列。如果 ϵ < εth，我们有

$$P_e(C_n,\epsilon )\le O(ex{p}^{-\beta n^{\alpha \log (d_v-1)}})\text{\hspace{1em}(13)}$$
对于一些正常数 α 和 β。

证明：让 $P_B^{MP}$ (Cn, ε)是在 BEC( ϵ)上对码 Cn 进行 MAP 解码的块错误概率。那么，我们有

$$P_e(C_n,\epsilon )\le P_B^{MP}(C_n,\epsilon )\le n{P}_b^{MP}(C_n,\epsilon )\text{\hspace{1em}(14)}$$

$$\le O(ex{p}^{-\beta n^{\alpha \log (d_v-1)})}\text{\hspace{1em}(15)}$$

VIII. 性能评估

在本节中，我们使用 MATLAB R2012a 在一台装有 2.50 GHz Intel CPU、8GB RAM 和 Windows 10 操作系统的台式电脑上评估所提出方案的性能。

A. 提出方案的开销

我们考虑了 ϵ-AU₂ 哈希函数的时间成本、Alice 处的编码以及 Bob 处的验证。按照第 VII-C 节中提到的方法，我们生成了三个 LDPC 码集合 C(x3, x6)：C(504, 252)、C(1008, 504)和 C(10080, 5040)。图 7 显示了码 C(1008, 504)的奇偶校验矩阵的稀疏模式。在我们的实验中，它们的对偶码将被用于所提出的认证方案中。值得注意的是，算法 2 和算法 3 基于算法 1，并且前两个算法的时间复杂度严重依赖于最后一个算法。因此，我们只需要考虑算法 1 的开销。

取 τ0 = 50，图 8 显示了在不同 θ 值下，哈希、编码和验证的时间成本与 τ 的关系，其中使用了 C(10080, 5040)的对偶码。可以看出：(1) 两者的时间成本对 τ 的值呈近线性依赖；(2) θ 的值越大，相应线的斜率越大；(3) 哈希的时间成本几乎占据了编码和验证总成本的 99.5%。

为了进一步降低时间成本，一种可能的解决方案是使用并行方法进行哈希计算。注意，可以直接从第 VII-B 节中提出的哈希方案中修改一个使用 π 个处理器具有时间复杂度(τ0 + 1)θ + 1 的并行算法。另一种可能的解决方案是使用现有的轻量级密钥哈希函数，如 MD5、SHA1、SHA2 和 SHA3。该方法的负面影响是会削弱所提出方案的安全性。

B. 提出方案的效率

表 II 显示了在不同参数设置下算法 1 的认证率，其中 τ0 = 50。由于 C(x3, x6)的密度演化阈值是 0.429，即 ϵth = 0.429。根据定理 4，由使用[21, 算法 4]生成的大回环(3, 6)-规则 LDPC 码序列在 BEC( ϵ)上的块错误概率可以是指数级的（以 n 为单位）小，当 ϵ < 0.429。根据定理 3，如果窃听者的信道（即，从 Alice 到 Carol 的信道）可以相对于擦除信道 W₂ = BEC(ζ)随机降级，其中 ζ > 1 - εth = 0.571，所提出的认证方案在表 II 中的不同参数设置下是安全的，认证率如下，其中 log|M|是消息的长度。

从表 II 中，我们发现认证率随着 LDPC 码的长度增加而降低。为了进一步提高认证率，只需要对我们的方案进行微小的修改。让 LDPC 码是 C(n, r)。算法 1 中 v 的最大值是 n - r，即存在最多 n - r 个线性独立的向量从{0, 1}ⁿ/C(n, r)中。让˜v 是一个正整数，满足˜v ≤ ⌊(n-r)/θ⌋。记 v = ˜vθ，让 r1, r2, …, rv 是来自{0, 1}ⁿ/C(n, r)的线性独立向量。定义一个新的哈希族为
$${\tilde{\varphi }}_{\tilde{k}}={\varphi }_{k_1}\times \cdots \times {\varphi }_{k_{\tilde{v}}}\text{\hspace{1em}(16)}$$

对于任何 $\tilde{k}$ = (k1, …, $k_{\tilde{v}}$) ∈ $K^{\tilde{v}}$，其中 M = {0, 1}${}^{\tau }\theta$，T = ${0,1}^{\theta }$，K = {0, 1}${}^{2\theta }$，且 ${\phi }_k$ : M → T。对于任何 $\tilde{m}$ = (m₁, …, m$\tilde{v}$) ∈ M，标签可以通过
$$\hat{t}=(t1,...,tv)=\hat{\phi }k(\hat{\phi }m)\text{\hspace{1em}(17)}$$
计算得出。

很明显，如果 { φ k ~ } k ~ \{φ_{\tilde{k}}\}_{\tilde{k}} {φk~​}k~​ 是 ϵ-AU2 的，那么 { φ k } k \{φ_k\}_{k} {φk​}k​ 也是 ϵ-AU2 的。修正后的方案遵循算法 1 的编码过程和验证过程，通过用 m 替换 $\tilde{m}$，用 k 替换 $\tilde{k}$，以及用 { φ k } k \{φ_k\}_{k} {φk​}k​ 替换 { φ k ~ } k ~ \{φ_{\tilde{k}}\}_{\tilde{k}} {φk~​}k~​。修正方案的性能在表 III 中给出。结果表明，与旧方案相比，修正方案的认证率显著提高，特别是在大码长场景下。

C. 提出方案的性能

表 III 显示了在不同参数设置下修正方案的性能。可以看出，与原始方案相比，修正方案的认证率显著提高，尤其是在大码长的情况下。

IX. 结论

在本文中，我们提出了一种高效实用的无线通信多消息认证方案，以提供数据完整性和识别。所提出的方案可以通过利用轻量级 ϵ-AU₂ 哈希函数和大回环 LDPC 码的对偶来实现完美安全性。理论分析已经验证了所提出的方案在给定 Eve 可以通过审查 Alice 认证的消息的多项式数量，并且可以自适应地发起多项式数量的攻击时是完美安全的。模拟结果也提供了，以证明所提出的方案可以实现高认证率和低时间延迟。未来的工作将开发一种针对高斯二进制输入窃听信道模型的计算效率高的方案。

附录

附录我就不翻译了吧。。。。。

参考文献

[1] J. G. Andrews et al., “What will 5G be?” IEEE J. Sel. Areas Commun., vol. 32, no. 6, pp. 1065–1082, Jun. 2014.
[2] N. Zhang et al., “Software defined networking enabled wireless network virtualization: Challenges and solutions,” IEEE Netw., vol. 31, no. 5, pp. 42–49, May 2017.
[3] K. Zhang, K. Yang, X. Liang, Z. Su, X. Shen, and H. H. Luo, “SecuriSecurity and privacy for mobile healthcare networks: From a quality of protection perspective,” IEEE Wireless Commun., vol. 22, no. 4, pp. 104–112, Aug. 2015.
[4] G. J. Simmons, “Authentication theory/coding theory,” in Adᵥances in Cryptology-CRYPTO. New York, NY, USA: Springer-Verlag, 1985, pp. 411–431.
[5] U. M. Maurer, “Authentication theory and hypothesis testing,” IEEE Trans. Inf. Theory, vol. 46, no. 4, pp. 1350–1356, Jul. 2000.
[6] A. D. Wyner, “The wire-tap channel,” Bell Syst. Tech. J., vol. 54, pp. 1355–1387, Oct. 1975.
[7] I. Csiszár and J. Köner, “Broadcast channels with confidential messages,” IEEE Trans. Inf. Theory, vol. IT-24, no. 3, pp. 339–348, May 1978.
[8] D. Chen et al., “S2M: A lightweight acoustic fingerprints-based wireless device authentication protocol,” IEEE Internet Things J., vol. 4, no. 1, pp. 88–100, Feb. 2017.
[9] Y. Zhu, L. Wang, K.-K. Wong, and R. W. Heath, “Physical layer security in large-scale millimeter wave ad hoc networks,” in Proc. IEEE Globcom, Washington, DC, USA, Dec. 2016, pp. 4–8.
[10] L. Lai, H. El Gamal, and H. V. Poor, “Authentication over noisy channels,” IEEE Trans. Inf. Theory, vol. 55, no. 2, pp. 906–916, Feb. 2009.
[11] D. Chen, S. Jiang, and Z. Qin, “Message authentication code over a wiretap channel,” in Proc. ISIT, 2015, pp. 2301–2305.
[12] J. Bao, X. Gao, X. G. Xu, R. Guo, and B. Jiang, “Low rate QC LDPC codes with reconfigurable structures for space information networks,” J. Commun., vol. 11, no. 3, pp. 255–262, Mar. 2016.
[13] R. G. Maunder, “A vision for 5G channel coding,” AccelerComm, Hampshire, U.K., White Paper, 2016. [Online]. Available: https://www.accelercomm.com/download/pdf/5G-Channel-Coding.pdf
[14] U. Maurer and S. Wolf, “Secret-key agreement over unauthenticated public channels—Part I: Definitions and a completeness result,” IEEE Trans. Inf. Theory, vol. 49, no. 4, pp. 822–831, Apr. 2003.
[15] R. Ahlswede and I. Csiszar, “Common randomness in information theory and cryptography. II. CR capacity,” IEEE Trans. Inf. Theory, vol. 44, no. 1, pp. 225–240, Jan. 1998.
[16] N. Zhang, N. Cheng, N. Lu, X. Zhang, J. W. Mark, and X. Shen, “Partner selection and incentive mechanism for physical layer security,” IEEE Trans. Wireless Commun., vol. 14, no. 8, pp. 4265–4276, Aug. 2015.
[17] X. Fang, N. Zhang, S. Zhang, D. Chen, X. Sha, and X. Shen, “On physical layer security: Weighted fractional Fourier transform based user cooperation,” IEEE Trans. Wireless Commun., vol. 16, no. 8, pp. 5498–5510, Aug. 2017.
[18] L. H. Ozarow and A. D. Wyner, “Wire-tap channel II,” ATT Bell Lab. Tech. J., vol. 63, no. 10, pp. 2135–2157, 1984.
[19] A. Thangaraj, S. Dihidar, A. R. Calderbank, S. W. McLaughlin, and J.-M. Merolla, “Applications of LDPC codes to the wiretap channel,” IEEE Trans. Inf. Theory, vol. 53, no. 8, pp. 2933–2945, Aug. 2007.
[20] A. T. Suresh, A. Subramanian, A. Thangaraj, M. Bloch, and S. W. McLaughlin, “Strong secrecy for erasure wiretap channels,” in Proc. IEEE Inf. Theory Workshop, Dublin, Ireland, Sep. 2010, pp. 1–5.
[21] A. Subramanian, A. Thangaraj, M. Bloch, and S. W. McLaughlin, “Strong secrecy on the binary erasure wiretap channel using large-girth LDPC codes,” IEEE Trans. Inf. Forensics Security, vol. 6, no. 3, pp. 585–594, Sep. 2011.
[22] J. Jin, C. Xiao, M. Tao, and W. Chen, “Linear precoding for fading cognitive multiple-access wiretap channel with finite-alphabet inputs,” IEEE Trans. Veh. Technol., vol. 66, no. 4, pp. 3059–3070, Apr. 2017.
[23] Y. Wu et al., “Low-complexity MIMO precoding for finite-alphabet signals,” IEEE Trans. Wireless Commun., vol. 16, no. 7, pp. 4571–4584, May 2017.
[24] E. Hof and S. Shamai (Shitz), “Secrecy-achieving polar-coding,” in Proc. IEEE Inf. Theory Workshop, Dublin, Ireland, Sep. 2010, pp. 1–5.
[25] H. Mahdavifar and A. Vardy, “Achieving the secrecy capacity of wiretap channels using polar codes,” IEEE Trans. Inf. Theory, vol. 57, no. 10, pp. 6428–6443, Oct. 2011.
[26] V. Korzhik, V. Yakovlev, G. Morales-Luna, and R. Chesnokov, “Performance evaluation of keyless authentication based on noisy channel,” in Proc. MMM-ACNS, Heidelberg, Germany, 2007, pp. 115–126.
[27] P. Baracca, N. Laurenti, and S. Tomasin, “Physical layer authentication over MIMO fading wiretap channels,” IEEE Trans. Wireless Commun., vol. 11, no. 7, pp. 2564–2573, Jul. 2012.
[28] A. Ferrante, N. Laurenti, C. Masiero, M. Pavon, and S. Tomasin. (2013). “On the achievable error region of physical layer authentication techniques over Rayleigh fading channels.” [Online]. Available: https://arxiv.org/abs/1303.0707
[29] S. Jiang, “Keyless authentication in a noisy model,” IEEE Trans. Inf. Forensics Security, vol. 9, no. 6, pp. 1024–1033, Apr. 2014.
[30] S. Jiang, “On the Optimality of Keyless Authentication in a Noisy Model,” IEEE Trans. Inf. Forensics Security, vol. 10, no. 6, pp. 1250–1261, Jun. 2015.
[31] D. Chen, N. Cheng, N. Zhang, K. Zhang, Z. Qin, and X. Shen, “Multimessage authentication over noisy channel with polar codes,” in Proc. IEEE MASS, Orlando, FL, USA, Oct. 2017, pp. 46–54.
[32] S. Fang, Y. Liu, and P. Ning, “Mimicry attacks against wireless link signature and new defense using time-synched link signature,” IEEE Trans. Inf. Forensics Security, vol. 11, no. 7, pp. 1515–1527, Jul. 2016.
[33] W. Wang, Z. Sun, S. Piao, B. Zhu, and K. Ren, “Wireless physical-layer identification: Modeling and validation,” IEEE Trans. Inf. Forensics Security, vol. 11, no. 9, pp. 2091–2106, Sep. 2016.
[34] T. Richardson and R. Urbanke, Modern Coding Theory. Cambridge, U.K.: Cambridge Univ. Press, 2008.
[35] D. Chen, Z. Qin, X. Mao, P. Yang, Z. Qin, and R. Wang, “SmokeGrenade: An efficient key generation protocol with artificial interference,” IEEE Trans. Inf. Forensics Security, vol. 8, no. 11, pp. 1731–1745, Nov. 2013.
[36] Q. Wang, K. Xu, and K. Ren, “Cooperative secret key generation from phase estimation in narrowband fading channels,” IEEE J. Sel. Areas Commun., vol. 30, no. 9, pp. 1666–1674, Oct. 2012.
[37] M. Bloch and J. Barros, Physical-Layer Security: From Information Theory to Security Engineering. Cambridge, U.K.: Cambridge Univ. Press, 2011.
[38] I. Csiszár, “Almost independence and secrecy capacity,” Problems Inf. Transmiss., vol. 32, no. 1, pp. 40–47, 1996.
[39] B. den Boer, “A simple and key-economical unconditional authentication scheme,” J. Comput. Security, vol. 2, no. 1, pp. 65–71, 1993.
[40] J. H. Silverman, “Fast multiplication in finite field GF (2^n),” in Proc. CHES, 1999, pp. 122–134.
[41] R. Safavi-Naini and P. R. Wild, “Information theoretic bounds on authentication systems in query model,” IEEE Trans. Inf. Theory, vol. 54, no. 6, pp. 2426–2436, Jun. 2008.

翻译致谢：感谢翻译过程中帮到我的 Kimi 翻译通、Quicker 公式识别3 动作、VSCode 编辑器、小绿鲸。