切比雪夫阻抗变换器设计与仿真

一、切比雪夫阻抗变换器简介
  阻抗变换器是一种常用的双端口元件，通过插入阻抗变换器可以消除因负载和传输线特性阻抗不 匹配而产生的反射．理论上说，一段 1/4 波长的均匀传输线就可以实现阻抗变换的功能，但只能在很窄的频带上工作，通过增加阻抗变换器的节数可以在较宽的频带上获得理想的匹配特性．在工程设计上一个重要的课题是对于给定的频响特性，应该用什么样的结构来实现，即网络综合问题．
  切比雪夫阻抗变换器是一类很常用的多节阻抗变换器，它的频响曲线为切比雪夫函数的平方，其主要特点是通带内具有等波纹的特性，且在通带内最大反射系数和总长度固定的情况下具有最宽的频带．
二、设计过程
   设计切比雪夫阻抗变换器的核心就是使Г(θ)等于切比雪夫多项式，因为切比雪夫多项式具有这类变换器所需的最佳特性。所以我们首先要讨论切比雪夫多项式的特性，然后用小反射理论推导出切比雪夫阻抗变换器的设计步骤。
 
1.切比雪夫多项式
   第n阶切比雪夫多项式是用Tn(x)表示的n次多项式。前四阶切比雪夫多项式是
T1(x) = x,
T2(x) = 2x^2 − 1,
T3(x) = 4x^3− 3x,
T4(x) = 8x^4 −x^2 + 1.
   更高阶的多项式可以由下面的递归公式求出：
Tn(x) = 2xTn−1(x) − Tn−2(x).
   前四项切比雪夫多项式如下图所示，从中可以看出切比切夫多项式的以下非常有用的性质：
  1.对于−1≤x≤1，| Tn(x)|≤1。在此范围内，切比雪夫多项式在±1之间振荡。这是等纹波特性，该区域将映射到匹配变压器的通带。
2.  对于|x|>1、| Tn(x)|>1。该区域将映射到通带以外的频率范围。
3.  对于|x|>1，| Tn(x)|会随着x和n的增加而快速增加。

  现在令x=cosθ，其中|x|<1。然后可以证明切比雪夫多项式可以表示为
Tn(cos θ) = cos nθ,
  或者更一般地表示为
Tn(x) = cos(n cos−1 x) for |x| < 1,
Tn(x) = cosh(n cosh−1 x) for x > 1.
  我们希望变换器的通带响应具有相等的波纹，因此需要将θm与x=1对应，π−θm与x=−1对应，其中θm和π−θm分别是通带的上下边缘，这可以通过将cosθ在上式中替换为cosθ/cosθm来完成：
    
  则对于 θm <θ<π − θm有|sec θm cos θ| ≤ 1，所以在同样的范围内有 |Tn(sec θm cos θ)| ≤ 1。

  由于 cos^n(θ)可以展开为cos(n-2m)θ形式的多项和，所以切比雪夫多项式可以改写为以下有用的形式：

T1(sec θm cos θ) = sec θm cos θ
T2(sec θm cos θ) = sec2 θm(1 + cos 2θ) – 1
T3(sec θm cos θ) = sec3 θm(cos 3θ + 3 cos θ) − 3 sec θm cos θ
T4(sec θm cos θ) = sec4 θm(cos 4θ + 4 cos 2θ + 3) −4 sec2 θm(cos 2θ + 1) + 1
 
2.切比雪夫阻抗变换器的设计
  我们现在可以通过使Г(θ)与TN(sec θm cos θ)成比例来综合一个切比雪夫等纹波通带，其中N是变换器的节数。
Г(θ) = 2e− j Nθ [0 cos Nθ + 1 cos(N − 2)θ +···+ n cos(N − 2n)θ + · · ·]
= Ae− j Nθ TN (sec θm cos θ),
  我们可以通过令θ=0求出常数A：
        
  如果通带中的最大允许反射系数大小为Гm，则Гm=|A|，因为通带中的最大值TN(sec θm cos θ)是1.因此，使用近似法可得出θm为
        

  进而计算出相对带宽：
            

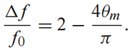
  上面的结果是近似的，因为它是以小反射理论为依据的。更多的示例可见下表：

3. 具体计算
  本文设计的三阶切比雪夫变换器用于将100Ω阻抗变换为50Ω。将N=3，A=Г(θ)=0.05代入前文公式可得：
 
cos 3θ:  2Г0 = A sec^3 θm,  Г0 = 0.0698;
cos θ:  2Г1 = 3A(sec^3 θm − sec θm),  Г1 = 0.1037.
 
 由对称性可得：
 
Г3 = Г0 = 0.0698,
Г2 = Г1 = 0.1037.

 那么，特征阻抗为：

n = 0:   ln Z1 = ln Z0 + 2Г0 = ln 50 + 2(0.0698) = 4.051
Z1 = 57.5Ω ;
n = 1:   ln Z2 = ln Z1 + 2Г1 = ln 57.5 + 2(0.1037) = 4.259
Z2 = 70.7 Ω;
n = 2:   ln Z3 = ln Z2 + 2Г2 = ln 70.7 + 2(0.1037) = 4.466
Z3 = 87.0 Ω

三、指标

频段：100MHZ～400MHz
VSWR＜1.5

四、仿真结果与分析
  本文设计的三阶切比雪夫变换器用于将100Ω阻抗变换为50Ω。使用仿真软件ADS，原理图如下：

得到的驻波比图像：

S（1，1）图像如下：

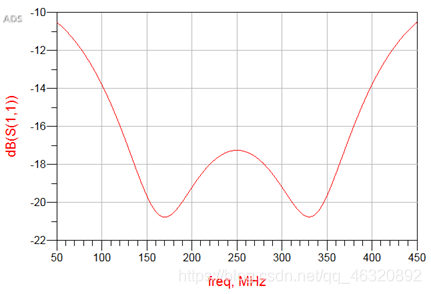
  由图像可见该变换器的驻波比在100MHz到400MHz之间均小于1.5，符合指标要求。

五、参考文献

[1]David M. Pozar 《微波工程》 ［M］ ． 3 版． 北京: 电子工业出版社， 2009:209-219．

 
 
本文内容是一次课程作业的报告。才疏学浅，如有纰漏，恳请指正。