【GCN_ICLR2017】论文笔记001：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS（理解+推导+翻译）

声明

本文仅供自己学习、和未来查阅所用，如果有错误欢迎大家批评指正，如果有存在内容使用而未标注出处，可联系下我！！

原文连接：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
Code relizes in github（By Tensorflow）：Graph Convolutional Networks To Implement
Code reliaze By Pytorch：Graph Convolutional Networks To Implement

---

SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

Author：

• ①Thomas N. Kipf（University of Amsterdam）
• ②Max Welling（University of Amsterdam、Canadian Institute for Advanced Research）

基于图卷积网络的半监督分类

Abstract

• 提出模型（即基于图结构数据的半监督学习方法，高效、可扩展）：卷积神将网络的有效变体，能够在图上直接操作
• 谱图卷积（spectral graph convolutions）的局部一阶近似$⟶$确定模型图卷积结构
• 该模型能够在图的边数上进行线性缩放
• 该模型能够学习隐藏层表示（隐藏层表示可以编码局部图结构和节点的特征）
• 在引文网络和知识图数据上进行实验，证明该模型比其他模型有很大优势

1 Introduction

• ①基于图的半监督学习：对图结构数据(由很多节点构成)进行分类，标签只对一小部分节点有作用
  ②标签信息通过对基于显示图的某种形式正则化而被在图上平滑，比如在损失函数上使用图的拉普拉斯正则化：
  $$\pounds ={\pounds }_0+\lambda {\pounds }_{reg}$$
  $$with,{\pounds }_{reg}=\sum _{i,j}{A}_{i,j}||f(X_i)-f(X_j)|{|}^2=f(X{)}^T\Delta f(X)(1)$$
  其中${\pounds }_0$表示图中标签部分的监督损失，$f(\cdot )$可以是类似神经网络的可微函数，$\lambda$是权重，$X$是节点特征向量$X_i$的矩阵。
  $\Delta =D-A$表示无向图$G=(V,E)$的非归一化图拉普拉斯算子（无向图G图具有：N个节点$v_i\in V$, 边$(v_i,v_j)\in E$，一个相邻矩阵$A\in {\mathbb{R}}^{N\times N}$(二进制或者加权)和一个度矩阵$D_{i,i}={\sum }_j{A}_{ij}$）。
  ③公式（1）依赖于在图中的连接点可能共享相同标签的假设。然而，这种假设可能会限制建模能力，因为图边不一定要编码节点相似性，但可能包含额外的信息。

• ① 神经网络模型$f(X,A)$ 进行图结构的编码,对带标签的所有节点在监督目标${\pounds }_0$上进行训练，从而在损失函数中避免了基于显示图的正则化
  ② 在图的邻接矩阵中施加条件$f(\cdot )$将允许模型从监督损失${\pounds }_0$中分配梯度信息，并使其能够学习有标签和无标签节点的表示

• 两贡献：
  ① 为神将网络模型引入层智能传播规则（简单、表现好）：该规则直接作用于图，且展示其是如何从谱图卷积一阶近似中获取$(Hammondetal.,2011)$
  ② 证明了这种基于图的神经网络模型在图中如何被用于节点的快速和可扩展的半监督分类。
  结论：在大量数据集上的实验表明，我们的模型在分类精度和效率(以挂钟时间衡量)方面都优于最先进的半监督学习方法。

2 图的快速近似卷积

作者经过一些列推导，得出图卷积网络的最终形式（单层）：
$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})(2)$$
其中：

• $\tilde{A}=A+I_N$：带有自环的无向图的邻接矩阵，${\tilde{D}}_{ii}$为度矩阵， ${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$
• $W^{(l)}$: 待训练层权重矩阵，$I_N$: 单位矩阵
• 第$l$层的的输入矩阵（即，激活矩阵）为$H^{(l)}\in {\mathbb{R}}^{N\times D}$,其中$H^{(0)}=X$
• $\sigma (\cdot )$: 表示激活函数，如$ReLU(\cdot )=max(0,\cdot )$

2.1 谱图卷积

(1) 谱图卷积定义
将图的谱卷积定义为信号$x\in {\mathbb{R}}^N$（通常是节点的特征向量）与滤波器$g_{\theta }=diag(\theta )$在傅里叶域中的相乘(滤波器是以参数为$\theta \in {\mathbb{R}}^N$得到)，即：
$$g_{\theta }\ast x=U{g}_{\theta }{U}^{T}x(3)$$
其中：

• $U$是对称归一化拉普拉斯矩阵的特征向量矩阵,对称归一化的拉谱拉斯矩阵：
  $$L^{sys}=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}=U\Lambda U^T$$
  推导：
  $$\begin{array}{rl}{L}^{sys}& =D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}\\ & =D^{-\frac{1}{2}}(D-A)D^{-\frac{1}{2}}\\ & =D^{-\frac{1}{2}}D{D}^{-\frac{1}{2}}-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\\ & =I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\end{array}$$
  $$由于L^{sys}是对称矩阵,因此其特征向量矩阵U是正交矩阵,即U{U}^T=I_N$$
• $\Lambda$是$L$的特征值的对角矩阵,$U^{T}x$是$x$的傅里叶变换。
• 我们可以认为$g_{\theta }$是$L$的特征值的一个函数，如，$g_{\theta }(\Lambda )$：
  $$g_{\theta }=g_{\theta }(\Lambda )$$
• 拉普拉斯举证定义为: $L=D-A$（用于上文的推导）
• 而以下篇章中的$L$我的理解均是对称归一化矩阵，即$L^{sys}$。

(2)切比雪夫近似谱卷积

• 式（3）的计算成本很大，因为特征向量矩阵$U$的复杂度是$O(N^2)$。此外，对于大型图来说，$L$的特征分解计算代价也很大。为了解决这个问题，$Hammondetal.(2011)$指出$g_{\theta }(\Lambda )$可以很好的通过切比雪夫多项式$T_k(x)$到$K^{th}$截断展开来近似:
  $$g_{\theta }(\Lambda )\approx \sum _{k=0}^K{\theta }_k{T}_K(\tilde{\Lambda })(4)$$
  其中：
• 重新调整$\tilde{\Lambda }=\frac{2}{{\lambda }_{max}}\Lambda -I_N$。
• ${\lambda }_{max}$表示$L$的最大特征值。
• $\theta \in {\mathbb{R}}^K$是切比雪夫系数的向量。
• 切比雪夫多项式递归定义为：
  $$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x)$$
  $$其中:T_0(x)=1，T_1(x)=x$$

(3) 写回谱图卷积（图卷积神经网络中的单个卷积层）
对信号$x$与滤波器$g_{\theta }\prime$的卷积的定义，我们现在有:
$$g_{\theta }\ast x=\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x(5)$$
其中：

• $\tilde{L}=\frac{2}{{\lambda }_{max}}L-I_N$
• 易证$(U\Lambda U^T{)}^k=U\Lambda U^T$。

注意:此表达式现在是$K-localized$，因为它是拉普拉斯算子中的$K^{th}$-阶多项式,即它仅取决于离中央节点($K$阶邻域)最大$K$步的节点。$Defferrardetal.(2016)$使用这个$K-localized$卷积来定义在图上的卷积神经网络。

式（5）的复杂度为$O(|E|)$,即边数是线性的。

---

补充：公式（4）和公式（5）的证明补充：
① 数学归纳法证明：$U{T}_k(\tilde{\Lambda })U^T=T_k(U\tilde{\Lambda }{U}^T)$(在③中求解式（5）
会使用到)
数学归纳法证明思路：当n=1时，所证显然成立，假设n=k时成立，只需要证明n=k+1时所证成立即可
证明：
根据切比雪夫多项式定义$(T_0(x)=1，T_1(x)=x)$，已知：
$$\begin{array}{rl}U{T}_0(\tilde{\Lambda })U^T& =U{U}^T=1=T_0(U\tilde{\Lambda }{U}^T)\\ U{T}_1(\tilde{\Lambda })U^T& =U\tilde{\Lambda }{U}^T=T_0(U\tilde{\Lambda }{U}^T)\end{array}$$
成立
假设n=k>1成立，因此：
$$\begin{array}{rl}U{T}_{k-2}(\tilde{\Lambda })U^T& =T_{k-2}(U\tilde{\Lambda }{U}^T)\\ U{T}_{k-1}(\tilde{\Lambda })U^T& =T_{k-1}(U\tilde{\Lambda }{U}^T)\end{array}$$成立

当n=k+1时，根据切比雪夫多项式递推定义，可证得：
$$\begin{array}{rl}U{T}_k(\tilde{\Lambda })U^T& =2U\tilde{\Lambda }{T}_{k-1}(\tilde{\Lambda })U^T-U{T}_{k-2}(\tilde{\Lambda })U^T\\ & =2U\tilde{\Lambda }{U}^T[U{T}_{k-1}(\tilde{\Lambda })U^T]-U{T}_{k-2}(\tilde{\Lambda })U^T\\ & =2(U\tilde{\Lambda }{U}^T)T_{k-1}(U\tilde{\Lambda }{U}^T)-T_{k-2}(U\tilde{\Lambda }{U}^T)\\ & =T_k(U\tilde{\Lambda }{U}^T)\end{array}$$
因此，根据数学归纳法，证毕。

② 已知：$$\tilde{L}=U\tilde{\Lambda }{U}^T$$
③ 将①和②中公式带入卷积公式：
$$\begin{array}{rl}{g}_{\theta }\ast x& =U{g}_{\theta }{U}^{T}x\\ & =U{g}_{\theta }(\Lambda )U^{T}x\\ & =U(\sum _{k=0}^K{\theta }_k{T}_K(\tilde{\Lambda }))U^{T}x利用公式①\\ & =(\sum _{k=0}^K{\theta }_k{T}_K(U\tilde{\Lambda }{U}^T))x利用公式②\\ & =(\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L}))x(5)\end{array}$$

---

2.2 逐层（LAYER-WISE）线性模型

(1) 简化：K=1（2个参数的模型）

因此，图卷积神经网络模型可以通过堆叠多个式（5）形式的卷积层来建立。作者将分层卷积操作限制为$K=1$（式（5）），即关于L是一个线性函数，因此在图拉普拉斯谱上具有线性函数。

---

在GCN这个线性公式中，现在近似取${\lambda }_{max}\approx 2$,可以预期到GCN参数能够在训练中适应这种规模变化，式(5)简化为：
$$\begin{array}{rl}{g}_{\theta }\ast x& =\sum _{k=0}^K{\theta }_k{T}_K(\tilde{L})x\\ & =\sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\frac{2}{{\lambda }_{max}}L-I_N)x\\ & =\sum _{k=0}^K{\theta }_k^{\prime }{T}_k(L-I_N)x将{\lambda }_{max}\approx 2带入后所得\\ & =[{\theta }_0^{\prime }{T}_0(L-I_N)+{\theta }_1^{\prime }{T}_1(L-I_N)]x\\ & ={\theta }_0^{\prime }x+{\theta }_1^{\prime }(L-I_N)x由T_0(x)=1,T_1(x)=x获得\\ & ={\theta }_0^{\prime }x+{\theta }_1^{\prime }(I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}-I_N)xL=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\\ & ={\theta }_0^{\prime }x-{\theta }_1^{\prime }{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x\end{array}$$
即：$$g_{\theta }^{\prime }\ast x={\theta }_0^{\prime }x-{\theta }_1^{\prime }{D}^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}x(6)$$

上式中，有两个自由参数${\theta }_0^{\prime }和{\theta }_1^{\prime }$。过滤器参数可以在整个图中共享。这种形式的滤波器的连续应用有效第对节点的$k$阶领域进行卷积,其中 $k$ 是神经网络模型中连续滤波操作或卷积层的数量。

---

(2) 简化：K=1（一个参数）

进一步限制参数的数量，目的是解决过拟合和最小化每层的操作（例如矩阵乘法）数量可能是有益的。得到如下的公式：
$$g_{\theta }\ast x\approx \theta (I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})x(7)$$
其中：

• 令参数$\theta ={\theta }_0=-{\theta }_1$
• 注意目前$I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$在范围$[0,2]$存在有特征值，因此当在深度神经网络模型中使用该算子时，重复应用该算子会导致数值不稳定和梯度爆炸/消失
• 为解决上面的问题，引入$renormalizationtrick：$
  $$\begin{array}{r}{I}_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}⟶{\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}\end{array}$$
• 其中：$\tilde{A}=A+I_N，{\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$，即图上加上自环

进一步推导，因此式（7）的公式可以写成：
$$\begin{array}{r}{g}_{\theta }\ast x\approx \theta {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}x\end{array}$$
在添加一个激活函数$\sigma$，即可得到快速卷积公式：
$$H^{(l+1)}=f(H^l,A)=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$

• 其中参数$\theta$替代为$W^{(l)}$,$x$替代为$H^{(l)}$

(3) 推广：多通道的特征映射

将这个定义推广到具有C个输入通道（即每个节点的C维特征向量)和$F$个过滤器或特征映射的信号$X\in {\mathbb{R}}^{N\times C}$,公式如下：
$$Z={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X\Theta (8)$$
其中：

• $\Theta \in {\mathbb{R}}^{C\times F}$表示为过滤器参数矩阵
• $Z\in {\mathbb{R}}^{N\times F}$是卷积信号矩阵

这个过滤操作的复杂度为$O(\mid E\mid FC)$,因为$\tilde{A}X$能够有效地实现为稀疏矩阵与密集矩阵的乘积。
至此，以上就是从频域角度推导图卷神经网络的全部过程！！！

3 半监督节点分类

3.1 实例

接下来，考虑在具有对称邻接矩阵 A（二进制或加权）的图上采用一个两层的$GCN$用于对其进行半监督节点分类。

(1)预处理操作
首先在预处理步骤中计算：
$$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$
进一步，前向模型就能写成简单的形式：
$$Z=f(X,A)=softmax\left(\hat{A}ReLU\right(\hat{A}X{W}^{(0)}\left)W^{(1)}\right)(9)$$
其中：

• $W^0\in {\mathbb{R}}^{C\times H}$是输入到隐藏层（有H个特征）的权重矩阵
• $W^1\in {\mathbb{R}}^{H\times F}$是隐藏层到输出层的权重矩阵
• $softmax$激活函数为：
  $$softmax(x_i)=\frac{1}{Z}exp(x_i)$$
  其中：$Z={\sum }_{i}exp(x_i),softmax$作用于每一行

(2) 损失函数：交叉熵误差
对于半监督的多分类问题，我们使用交叉熵误差对所有的标记样本误差进行评估：
$$\mathcal{L}=-\sum _{l\in {\mathcal{Y}}_L}\sum _{f=1}^F{Y}_{lf}\ln Z_{lf}(10)$$
其中：

• ${\mathcal{Y}}_L$：表示带标签的节点集

(3) 训练

• 神经网络中的权重参数$W^{(0)}$和$W^{(1)}$使用梯度下降进行训练更新
• 每次训练迭代（即，epoch）使用完整的训练集进行批量梯度下降(前提: 数据集适合内存，当内存不够可适当调小训练批次)
• 邻接矩阵$A$使用稀疏矩阵表示，内存要求为$O(E)$,其中$E$为边数，即和边数呈线性关系
• 引入$Dropout$实现训练过程具有随机性
• 文章中说：未来进行关于内存效率扩展与小批量随机梯度下降工作

3.2 实现

在实践中，利用TensorFlow,采用稀疏-密集矩阵乘法的方法高效的在基于-GPU上实现了式(9)：
$$Z=f(X,A)=softmax\left(\hat{A}ReLU\right(\hat{A}X{W}^{(0)}\left)W^{(1)}\right)(9)$$
其中：

• 式(9)的计算复杂度为:$O(|E|CHF)$,即图中的边数呈现线性关系

4 相关工作

作者提出的模型灵感来源两个领域：

• 基于图的半监督学习
• 图中的神经网络

作者对这两个领域的相关工作进行简要的概括。

4.1 基于图的半监督学习

基于图的半监督学习方法分为两大类：

• 基于某种形式的显式图拉普拉斯正则化(标签传播、流行正则化、深度半监督嵌入)
• 基于图嵌入

4.2 图中的神经网络

• 介绍前人们(2015、2009)的在图上的神经网络框架需要重复的压缩映射作为传播函数，直到节点稳定
• 2015年，前人提出类似于卷积的图传播规则和图级分类方法（限制：学习节点度数特定的权重矩阵）
• 2016年，前人提出基于图的神经网络进行节点分类，但复杂度有$ O(N2 )$ ，限制可能的应用范围
• 作者，介绍自己模型：相对前人，提高了在大规模网络中的可扩展性和分类性能。

5 实验

模型测试的的实验任务：

• 半监督文本分类：引文网络
• 半监督实体分类：知识图谱中提取的二部图
• 多种图传播模型评价
• 随机图中运行时间分析

5.1 数据集

数据集统计如下：

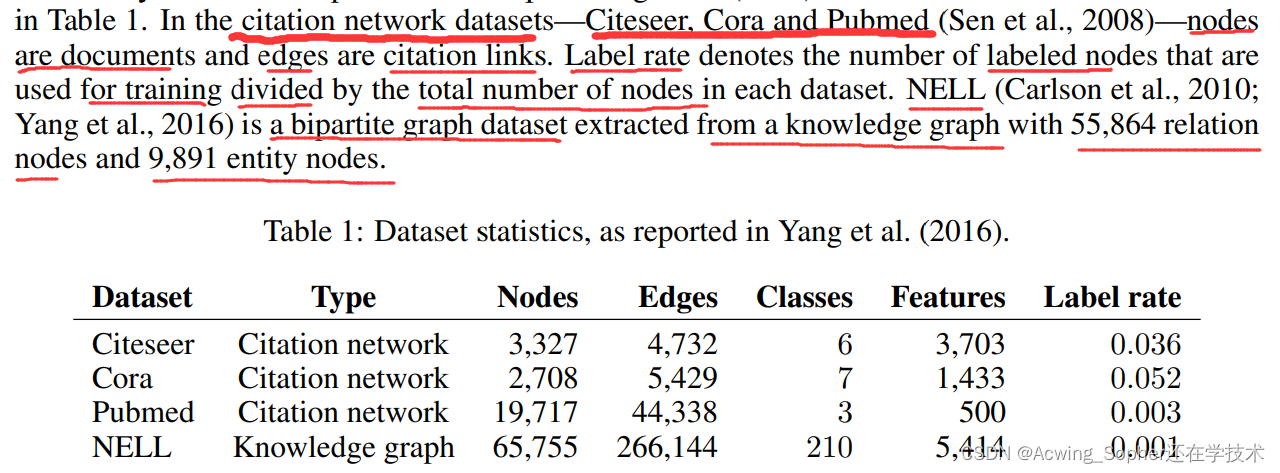
(1) Citation networks

• 三个引文网络数据集：Citeseer、Cora和PubMed
• 数据集中包含：
  ① 每个文档的稀疏bag-of-words特征向量
  ② 文档之间的引用链接列表
• 引用链接视为（无向）边，其构造为二元对称邻接矩阵$A$
• 每个文档都有一个类标签，训练时，每个类只使用20个标签，但包含所有的特征向量

(2) NELL

• 知识图谱是一组与有向标记边（关系）相连的实体
• 遵循$Yangetal.(2016)$所述的预处理方案
• 文中为每个实体对$(e_1,r,e_2)$分配单独的关系节点 $r_1$ 和 $r_2$ 作为 $(e_1,r_1)$ 和 $(e_2,r_2)$,实体节点由稀疏特征向量描述
• 通过为每个关系节点分配一个唯一的one-hot表示来扩展NELL中的特征数量，从而有效地为每个节点生成61278维稀疏特征向量
• 半监督任务只考虑训练集中每个类一个标记示例的极端情况。如果节点 $i$和 $j$ 之间存在一条或多条边，通过设置 $A_{ij}=1$,从该图中构造一个二元对称邻接矩阵

(3) Random graphs

• 通过模拟大小不同的随机图数据集进行测量每个epoch的训练时间。对于$N$节点数据集，创建一个随机图，随机均匀地分配$2N$条边。将单位矩阵$I_N$作为输入矩阵$X$，进而隐含地采用无特征方法，其中模型仅被告知每个节点的身份，节点由唯一的$one-hot$向量指定。 我们为每个节点添加dummy标签 $Y_i=1$

5.2 实验布置

说明：

• 按照3.1部分进行两层的GCN实验，且在具有1000标记样本的测试集上进行评估预测
• 附录 B 中提供了使用最多 10 层的更深模型的额外实验

参数设置

• 优化器：Adam，学习率设置为0.01
• 最大200 epoch
• 停止条件：连续10个epoch中，验证集损失没有减少
• 归一化输入特征向量：行归一化
• 权重初始化：采用在$Glorot\&Bengio(2010)$ 中描述的方法
• 随机图数据集上：隐藏层32个单元，省略dropout和L2正则化

5.3 基准

(1) 与$Yangetal.(2016)$的相同基线方法进行比较，即:

• $labelpropagation(LP)$
• $semi-supervisedembedding(SemiEmb)$
• $manifoldregularization(ManiReg)$
• $skip-grambasedgraphembeddings(DeepWalk)$
• 省略$TSVM$,其它不能扩展到一个数据集中的大量类

(2) 与$Lu\&Getoor(2003)$提出的迭代分类器算法$(ICA)$以及结合两个逻辑回归分类器进行比较
(3) 与$Planetoid$进行比较，选择其最好的模型变体作为基线

6 结果

6.1 半监督节点分裂

(1) 对于$Citeseer,CoraandPubmed$三个数据集使用如下的超参数：

• $dropoutrate$:0.5
• $L2regularization$:$5\cdot 10^{-5}$
• 隐藏单元数量：16

(2) 对于$NELL$数据集使用如下超参数：

• $dropoutrate$:0.1
• $L2regularization$:$1\cdot 10^{-5}$
• 隐藏单元数量：64

6.2 传播模型的评价

表中的数字表示使用随机权重矩阵初始化的 100 次重复运行的平均分类准确度。在每层${\Theta }_i$有多个变量的情况下，文中对第一层的所有权重矩阵施加$L2$正则化。

6.3 每个epoch的训练时间

在模拟随机图上进行100个epochs的训练，得到每个epoch（包括：前向传播、交叉熵计算、后向传播）的平均时间的结果，以秒为单位的wall-clock时间。

解释Wall-clock时间：响应时间，指计算机完成某一个任务所花的全部时间，也叫墙上时间（wall clock）或流逝时间(elapsed time)。

7 讨论

7.1 半监督模型

• 与$basedongraph-Laplacianregularization、Skip-gram$相比，模型有优势
• 模型在时间效率方面也很不错，且特征信息传播过程中能提高分类效果
• $renormalizationtrick$作用：①效率提高(更少的参数和操作，如乘法或加法)、②更好的预测性能

7.2 局限性和未来工作

(1) Memory requirement

• 使用全批次梯度下降，内存和数据集成线性关系
• 对大数据，如果$GPU$不行，可使用$CPU$代替或者可尝试小批量随机梯度下降
• 当使用小批量随机梯度下降，要考虑GCN模型中的层数（K 层GCN 的 K 阶邻域必须存储在内存中为了进行精确的过程）
• 对于非常大且连接紧密的图数据集，需要进一步处理近似

(2) Directed edges and edge features

• 局限：框架目前并不自然地支持边缘特征，并且仅限于无向图(加权或非加权)
• 解决办法：通过将原始有向图表示为无向二分图以及表示原始图中边的附加节点，进而实现处理有向边和边缘特征

(3) Limiting assumptions
文中在前部分介绍邻接矩阵只介绍：$\tilde{A}=A+I_N$的由来及作用。但对于某些数据集，在$A$的定义中引入一个权衡参数λ可能是有益的：
$$\tilde{A}=A+\lambda I_N$$

8 结论

我们的GCN模型使用了一种高效的分层(layer-wise)传播规则，该规则基于图上的谱卷积的一阶近似。通过实验，证明所提出的 GCN 模型能够以对半监督分类有用的方式对图结构和节点特征进行编码。

---

图卷积网络具有的特点：

(1) 局部特性

• GCN关注的是图中以某节点为中心，其$K$阶领域内的相邻信息，这一点**与GNN有本质的区别

(2)一阶特性

• 经过多种近似之后，GCN变成了一个一阶模型（即，单层的GCN可以被用于处理图中一阶领域内的信息),若要处理K阶领域，可以采用多层GCN来实现

(3)参数共享

• 对于每个节点，其上的权重矩阵(即，过滤器参数)$W$是共享的

参考

[1]GCN - Semi-Supervised Classification with Graph Convolutional Networks 用图卷积进行半监督节点分类 ICLR 2017
[2]https://blog.csdn.net/qq_35812205/article/details/120575563

$QWQ，如果错误，请点出，相互学习！！！！$