
开源内容:https://github.com/TommyZihao/zihao_course/tree/main/CS224W
子豪兄B 站视频:https://space.bilibili.com/1900783/channel/collectiondetail?sid=915098
斯坦福官方课程主页:https://web.stanford.edu/class/cs224w
目录
PageRank冷知识
- Google最早的搜索引擎算法。给每个网页重要度打分,高分靠前。Page既有“网页”的意思,也有“拉里·佩奇”的意思
- 两位作者当年只有24岁,是斯坦福大学的phD
- 谷歌最早的办公场地是车库里的乒乓球桌
- 1997年之前的搜索引擎︰网页收录少、相关率20%、排序效果差
- 1997年之后,斯坦福大学Google搜索结果,相关率80%
- 搜索引擎成为互联网第一个Killer App,开启互联网时代PageRank申请专利后,谷歌一举超过雅虎、微软
- 拉里·佩奇凭借PageRank,在30岁当选美国工程院院士
- 斯坦福大学拥有超过1%的Google股票。收益超过10亿美元
PageRank简介
PageRank是1997年谷歌第一代搜索引擎的底层算法。大幅提高了搜索结果的相关率和质量,成为互联网第一个爆款应用,造就了传奇的谷歌公司。
应用场景
PageRank把互联网表示为由网页节点和引用链接构成的有向图,通过链接结构,计算网页节点重要度。来自重要网页节点的引用链接,权重更高。

理解PageRank的五种角度
我们可以通过线性方程组、矩阵乘法、特征值和特征向量、随机游走、马尔科夫链这五种角度,理解并求解PageRank值。
线性方程组
重要节点引出的稀少链接,权重更高


矩阵乘法
迭代左乘M矩阵



特征值和特征向量
对于Column Stochastic矩阵,由Perreon-Frobenius定理︰最大的特征值为1,存在唯一的主特征向量(特征值1对应的特征向量),向量所有元素求和为1

随机游走
浏览者顺着连接随机游走,一个网页的访问次数比较多则说明这个网页比较重要



马尔科夫链
每个节点表示一种状态,节点之间的连接表示状态的转移,根据状态转移矩阵,可以计算下一个时刻的状态转移概率

求解PageRank
- 迭代求解线性方程组( O ( n 3 ) O(n^{3}) O(n3),不推荐)
- 迭代左乘M矩阵(推荐,幂迭代)
- 矩阵的特征向量( O ( n 3 ) O(n^3) O(n3),不推荐)
- 随机游走(需模拟很多游走,不推荐)
- 马尔科夫链(和求解矩阵特征向量等价,不推荐)
迭代左乘M矩阵


PageRank收敛性分析
Ergodic定理:如果满足irreducible(非彼此孤立)和aperiodic(非周期性质震荡)的马尔科夫链,则一定满足:
- 存在唯一的解 π \pi π
- 能从
π
0
\pi_0
π0收敛到
π
\pi
π


PageRank存在的问题

仅指向自己的节点(刷抖音刷的停不下来)
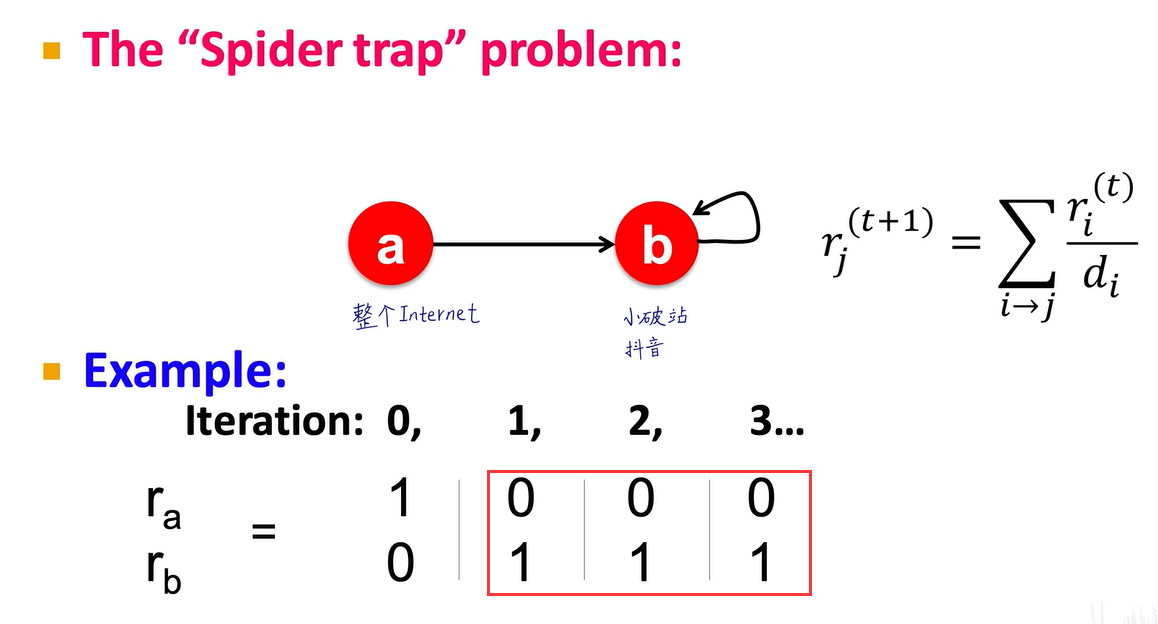
没有出连接(看到这个网页之后全部退网了)

违背了每一列求和为1的假设

PageRank解决方案




PageRank其它应用

-
寻找与指定节点最相似的节点(Proximity on graphs):同一个用户访问过的节点更可能是相似的(基本假设)
-
PageRank变种::将“随机传送到任一节点”优化为“随机传送到指定的一些节点”或“随机传送到指定的一个节点”,用访问次数来反映节点的亲疏远近。
- Topic-Specific PageRank或Personalized PageRank:随机传送到指定的一些节点
- Random Walk with Restarts:随机传送到指定的一个节点
代码实战
import networkx as nx # 图数据挖掘
import numpy as np # 数据分析
import random # 随机数
import pandas as pd
# 数据可视化
import matplotlib.pyplot as plt
import matplotlib as mpl
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
构建图并进行可视化
OpenKG-四大名著人物关系知识图谱和OWL本体:http://www.openkg.cn/dataset/ch4masterpieces
df = pd.read_csv('data/三国演义/triples.csv')
df

edges = [edge for edge in zip(df['head'], df['tail'])]
G = nx.DiGraph()
G.add_edges_from(edges)
# 可视化
plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, iterations=3, seed=5)
nx.draw(G, pos, with_labels=True)
plt.show()

对PageRank得分进行排名
pagerank = nx.pagerank(G, # NetworkX graph 有向图,如果是无向图则自动转为双向有向图
alpha=0.85, # Damping Factor
personalization=None, # 是否开启Personalized PageRank,随机传送至指定节点集合的概率更高或更低
max_iter=100, # 最大迭代次数
tol=1e-06, # 判定收敛的误差
nstart=None, # 每个节点初始PageRank值
dangling=None, # Dead End死胡同节点
)
sorted(pagerank.items(),key=lambda x : x[1], reverse=True)
用节点尺寸可视化PageRank值
# 节点尺寸
node_sizes = (np.array(list(pagerank.values())) * 8000).astype(int)
# 节点颜色
M = G.number_of_edges()
edge_colors = range(2, M + 2)
plt.figure(figsize=(15,14))
# 绘制节点
nodes = nx.draw_networkx_nodes(G, pos, node_size=node_sizes, node_color=node_sizes)
# 绘制连接
edges = nx.draw_networkx_edges(
G,
pos,
node_size=node_sizes, # 节点尺寸
arrowstyle="->", # 箭头样式
arrowsize=20, # 箭头尺寸
edge_color=edge_colors, # 连接颜色
edge_cmap=plt.cm.plasma,# 连接配色方案,可选:plt.cm.Blues
width=4 # 连接线宽
)
# 设置每个连接的透明度
edge_alphas = [(5 + i) / (M + 4) for i in range(M)]
for i in range(M):
edges[i].set_alpha(edge_alphas[i])
# # 图例
# pc = mpl.collections.PatchCollection(edges, cmap=cmap)
# pc.set_array(edge_colors)
# plt.colorbar(pc)
ax = plt.gca()
ax.set_axis_off()
plt.show()

总结
PageRank是1997年谷歌第一代搜索引擎的底层算法。大幅提高了搜索结果的相关率和质量,成为互联网第一个爆款应用,造就了传奇的谷歌公司。PageRank把互联网表示为由网页节点和引用链接构成的有向图,通过链接结构,计算网页节点重要度。来自重要网页节点的引用链接,权重更高。
我们可以通过线性方程组、矩阵乘法、特征值和特征向量、随机游走、马尔科夫链,五种角度,理解并求解PageRank值。之后对PageRank的收敛性分析并针对特殊节点的进行改进,最后扩展PageRank在推荐系统中计算节点相似度排序的升级变种。
在代码实战中,使用Networkx计算三国演义人物有向图的节点重要度。










 PageRank是谷歌早期搜索引擎的关键算法,通过链接结构计算网页重要性。它涉及线性方程组、矩阵乘法、特征值理论、随机游走和马尔科夫链等概念。文章介绍了PageRank的起源、解决的问题、收敛性分析及在实际中的应用,包括代码示例展示了如何使用NetworkX计算图的PageRank值。
PageRank是谷歌早期搜索引擎的关键算法,通过链接结构计算网页重要性。它涉及线性方程组、矩阵乘法、特征值理论、随机游走和马尔科夫链等概念。文章介绍了PageRank的起源、解决的问题、收敛性分析及在实际中的应用,包括代码示例展示了如何使用NetworkX计算图的PageRank值。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










