【遗传算法】模拟二进制交叉SBX与多项式变异

0 前言

Gitee 代码地址： https://gitee.com/futurelqh/GA

模拟二进制交叉：Simulated binary crossover

Introduction

• SBX 是模拟二进制编码的遗传算法中的单点交叉 ，对于后者简单示意图如下图所示:

交叉前后解码实数值的平均相等

$$\frac{p_1+p_2}{2}=\frac{c_1+c_2}{2}$$

交叉前后解码实数值差的商 ≈ 1

• 思想即为子代会离其父代较近(传播因子 β 定义为子女与父母之间距离的比值)
• Spread Factor 分布系数

$$\beta =|\frac{c_1+c_2}{p_1+p_2}|$$

Spread Factor 的分布 （β）

基于此，考虑一个长度为15 的二进制编码的个体，之间随机挑选所有可能的分割位点进行单点变异后的子代和父代计算的 β 数值，从而观察 β 的分布

Computer for Matlab

根据：

$$p_1+p_2=c_1+c_2(1)$$
$$\beta =|\frac{c_1+c_2}{p_1+p_2}|(2)$$
反解出子代：

$$c_1=1/2\ast (p_1+p_2)-1/2\ast \beta \ast (p_2-p_1)$$
$$c_2=1/2\ast (p_1+p_2)+1/2\ast \beta \ast (p_2-p_1)$$

通过概率密度函数拟合β

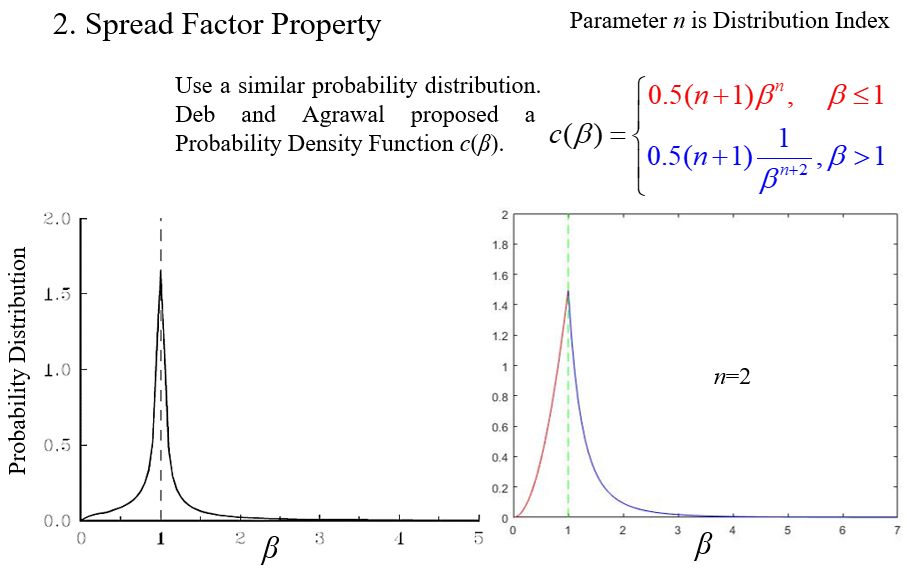
更大的分布指标 n 意味着子代和父代更接近

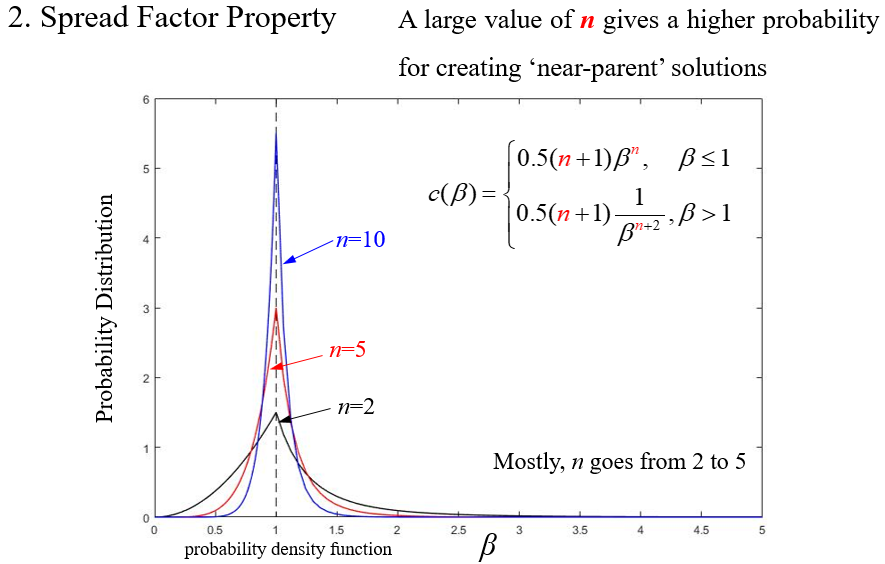
通过概率密度求出分布函数

conclusion

SBX 在实数编码中的运用

SBX MATLAB 代码实现

% Simulated binary crossover
beta = zeros(N, D);
mu   = rand(N , D);

beta(mu<=0.5) = (2*mu(mu<=0.5)).^(1/(disC+1));
beta(mu>0.5)  = (2-2*mu(mu>0.5)).^(-1/(disC+1));
beta = beta.*(-1).^randi([0, 1], N, D);
beta(repmat(rand(N, 1)>proC, 1, D)) = 1;

Offspring = [(Parent1+Parent2)/2 + beta.*(Parent1-Parent2)/2
             (Parent1+Parent2)/2 - beta.*(Parent1-Parent2)/2];

多项式变异

（2-11）式中 $v_k$ 表示上一代的种群，$v_{k^{{}^{\prime }}}$ 表示多项式变异后新产生的种群， $u_k$ 表示 upper ：变量的上界， $l_k$ 表示 lower ：变量的下界。 $(u_k-l_k)：{\Delta }_{max}$

• 在Deb K , Goyal M . A Combined Genetic Adaptive Search (GeneAS) for Engineering Design[C]// 1996.原文中，其是这样描述的

%% Polynomial mutation
% 定义变异的边界
MinValue = repmat(lower, N, D);
MaxValue = repmat(upper, N, D);

k    = rand(N,D); % 随机选定要变异的基因位
mu   = rand(N,D); % 采用多项式变异，此为式中的 u

Temp = k<=ProM & mu<0.5;   % 要变异的基因位，ProM：变异概率
Offspring(Temp) = Offspring(Temp)+(MaxValue(Temp)-MinValue(Temp))...
    .*((2.*mu(Temp)+(1-2.*mu(Temp)).*(1-(Offspring(Temp)-MinValue(Temp))./(MaxValue(Temp)-MinValue(Temp))).^(DisM+1)).^(1/(DisM+1))-1);

Temp = k<=ProM & mu>=0.5;
Offspring(Temp) = Offspring(Temp)+(MaxValue(Temp)-MinValue(Temp))...
    .*(1-(2.*(1-mu(Temp))+2.*(mu(Temp)-0.5).*(1-(MaxValue(Temp)-Offspring(Temp))./(MaxValue(Temp)-MinValue(Temp))).^(DisM+1)).^(1/(DisM+1)));

% 越界处理 
Offspring(Offspring>MaxValue) = MaxValue(Offspring>MaxValue); % 子代越上界处理
Offspring(Offspring<MinValue) = MinValue(Offspring<MinValue); % 子代越下界处理

Reference

[1] CSDN 字体编辑实例

[2] MarkDown 公式指导手册

[3] SBX(Simulated binary crossover)模拟二进制交叉算子和DE(differential evolution)差分进化算子 强推☆☆☆ 感谢作者的分享，受益匪浅，附原文在此