2018， Strategies for reducing the size of the search space in semantic genetic programming

本文链接：https://blog.csdn.net/qq_46450354/article/details/135440387

Abstract

在解决优化问题时，遗传编程(GP)算法应用生物启发操作(例如,交叉和变异)，以便在可能的解空间中找到满意的解决方案。通常，这类算法用于解决一个称为符号回归的问题，其目标是找到一个数学表达式，其对应的曲线近似由一组训练实例诱导的曲线。

典型的GP算子没有考虑到语义方面，这往往会恶化使用它们的方法的性能和鲁棒性。另一方面，语义遗传算子聚合了语义的概念，允许对搜索空间进行更一致的探索。另一个改进是利用n维语义空间中描述可能解之间空间关系的几何性质，其中n等于训练实例的数量。在此背景下通常作为参考的方法被称为几何语义遗传规划( Geometric Semantic Genetic Programming，GSGP )。然而，在n值较高的问题中- -在实际应用中的常见场景- -搜索过程可能变得过于复杂，因为语义空间的大小随着维度数的增加而呈指数增长。在本文中，我们旨在通过实例选择方法来减少语义遗传编程背景下搜索空间的维度，从而缓解这一问题。

我们的主要目标是设计、实现和验证减少搜索空间大小的方法。更准确地说，我们想了解语义空间维度的数量能够在多大程度上影响搜索过程，以及选择方法的应用对GSGP执行的搜索的影响。此外，我们试图理解噪声对遗传规划方法和所提出的实例选择策略的影响。

考虑了两种方法：(i)应用实例选择方法作为预处理步骤，即在GSGP提供训练实例之前；(ii)将实例选择纳入GSGP的进化过程，在一组真实世界和合成数据集上进行了实验。实验分析表明，所提出的一些方法实际上可以改进与GSGP执行的搜索相关的方面。

Keywords: Geometric Semantic Genetic Programming, Symbolic Regression, Instance Selection, Supervised Learning.

Introduction

进化计算是一个总括性的术语，用于指一组问题解决技术，其使用的计算模型受到著名的进化机制[福格尔, 2006]的启发。这些技术共享一个共同的概念基础，即通过模拟生物操作的过程来模拟个体结构的进化，并取决于这些结构的感知性能(适应度)，由它们周围的环境定义。

进化算法保持一个种群结构- -代表待求解问题的候选解- -根据选择规则和其他操作(如重组(又称交叉)和变异)进行进化。一个适应度值归属于种群中的每个个体，反映了其在环境中的行为。选择过程包含一个概率过程，能够将搜索引导到具有高适应度个体的区域，从而利用关于搜索空间的可用信息。重组和变异扰动了这些个体，为探索提供了一般性的启发。虽然从生物学家的观点来看，这些算法非常简单，但它们足够复杂，以提供健壮和强大的自适应搜索机制[Spears et al , 1993]。

在本文中，我们关注进化计算的一个分支，称为遗传编程(Genetic Programming，GP)，它与其他进化算法的区别在于将每个个体表示为一个可解释的程序，长度可变，通常表示为语法树(如图1.1所示)，为了评估其适应度，必须执行该语法树。在进化过程中，GP通过随机变换，逐代进化一个程序种群，这个种群进化成一个新的、有希望的更好的程序种群 population of programs [Banzhaf et al., 1998; Poli et al., 2008].

GP已经成功地用于解决一个称为符号回归的监督学习任务，在这个任务中，我们希望找到一个数学表达式，以符号形式表示。fits (或近似符合)是训练集中实例的集合。我们可以通过预测一组测试实例(其中,我们知道实际产出值)的输出值来衡量生成模型的质量。预测值与实际输出值的平均距离越小，模型越好。一旦找到一个令人满意的模型，我们就可以使用它来插值未知实例的输出值，这反过来又可以使我们进行预测，获得见解，并找到底层响应面中的最优区域。

传统上，GP通过使用两种不同的遗传算子(称为交叉和变异)来进化语法树的种群，它们的原始形式通过操纵父代的语法(即结构)来产生后代。这两种算子都保证得到的子代将代表有效个体，但都无法保证子代的行为在某种程度上与父代的行为相似。这一事实- -典型的GP算子在纯句法层面上(syntactic level)的作用意味着，子代个体往往代表更差的候选解，恶化了搜索过程。

考虑到这一点，研究人员专注于考虑个体的行为或语义的GP方法的概念。这些新方法将语义感知融入到进化过程中，修改搜索算子，使其产生与父代行为相似的后代[Vanneschi et al., 2014a]，迄今为止取得了很好的效果。

在监督学习环境中，程序的语义被描述为程序在应用于由训练实例集定义的输入集合时产生的输出的向量。这个向量可以表示为n维度量空间 $S$ (称为语义空间)中的一个点，其中n是训练集的大小。图1.2说明了对GP个体语义的评估及其在语义空间中的表示。目标输出- -即搜索到的真实值(actual values)的向量，由训练集中给定的输出定义–也可以在语义空间中表示。适应度值正比于将个体表示的函数应用到输入集合后生成的输出向量与目标输出向量之间的距离。在这种情况下，语义GP搜索中的目标可以看作是试图通过使 $S$ 中的个体更接近目标输出来修改 $S$ 中个体的语义。

图1.2：适应度评价和语义空间。在适应度评估过程中，GP方法将个体表示的函数应用到输入 $x$ 的集合中，生成一个输出向量 $y^′$ ，该向量可以在语义空间中表示。目标输出向量 $y$ 在语义空间中也是可表示的，个体的适应度与 $y$ 和 $y'$ 之间的距离成正比。

尽管语义GP方法带来了新的视角和优越的性能，但它们是间接的：它们的运算符作用于父代的语法以产生后代，如果满足某种语义标准，这些后代就被接受。Moraglio et al. [2012] 描述了与这种方法相关的两个缺陷：(i)它是非常浪费的，因为它严重基于试错法；(ii)它没有提供关于句法和语义搜索如何相互联系的见解。他们还提出了一个新的GP框架，能够操纵个体在语义空间中的配置具有几何意义的句法。该框架称为几何语义GP (Geometric Semantic GP，GSGP)，用几何语义算子代替传统的交叉和变异算子，利用语义感知和几何形状来描述父代和子代之间的空间关系，将精确的几何属性引入到语义空间中。基于欧氏距离的几何语义交叉算子，例如，返回父代的凸组合，在父代输出向量之间的片段中生成输出向量的子代。这些算子直接搜索程序的底层语义空间，从而产生一个单峰的适应度景观- -它可以通过进化算法进行优化，对几乎任何度量[Moraglio, 2011].都有很好的结果。

Castelli, M., Manzoni, L., and Vanneschi, L. (2012). An efficient genetic programming system with geometric semantic operators and its application to human oral bioavailability prediction. arXiv preprint arXiv:1208.2437.

通过构造，几何语义算子受到语义空间维度增加的影响。这种影响与搜索空间随维度数 $S$ 的指数增加所导致的维度灾难有关，而维度灾难取决于训练实例的数量。在这个数量很高的问题中- -在现实世界应用中的一个常见场景- -我们最终会有一个极大的搜索空间，更难搜索，并且可能会带来代表相同类型信息的不同实例。在这种情况下，通过减少实例的数量，我们自动降低了语义空间的维度数量，进而降低了其复杂度。直观上，随着复杂度的降低，可能的组合数量会减少，这可能会提高收敛到最优的速度。解决这一问题的新策略是本论文的主要目标。

除了使用GSGP代替GP的所有优点外，文献中的一些论文也声称，与经典的GP技术 [Vanneschi et al., 2013; Castelli et al., 2012, 2013a; Vanneschi et al., 2014b; Vanneschi, 2014]. 相比，GSGP对由噪声数据点引起的过拟合具有更强的鲁棒性。起初，这甚至可能是违背直觉的，因为GSGP导致的解的指数增长甚至会恶化过拟合的效果。然而，没有系统的研究来评估是否和/或在哪些情况下可能是真的，以及噪声数据点如何影响GSGP的性能。考虑到这一点，在深入到与语义空间的维度相关的问题之前，我们研究了噪声对GSGP执行回归的影响。

1.1 Motivation

在过去的几十年里，海量数据集的数量急剧增长，涵盖了电子商务、金融市场、图像处理和生物信息学等众多领域。超大型数据库的可用性不断挑战着机器学习和数据挖掘界提出快速、可扩展和准确的方法 [Peteiro-Barral and Guijarro-Berdiñas, 2013].

在符号回归情境下, 通过移除海量数据集的部分实例使得变得更小可以减少用于诱导回归模型的计算工作量。此外，实例可能集中在输入空间的某些特定区域，导致回归方法过度专门化模型来映射这些区域，而实例较少的区域没有得到必要的关注。在这种情况下，从这些密集区域中移除实例可以通过引入回归方法来考虑具有相似重要性 [Cardie and Howe, 1997] 的整个输入空间来改进诱导模型。减少训练集大小和语义空间维度的一种直观策略是通过执行机器学习文献中的数据实例选择 [Domingos, 2012]。

在GSGP背景下，正如我们所提到的，通过减小训练集的大小，语义空间的维度数量也随之减少，导致搜索空间更小更简单。图1.3说明了维度的数量如何可以修改搜索的一个方面。它描述了一个 $2 D$ 语义空间(也就是说, 训练集中只存在两个例子)，并给出了问题的两个候选解(父代 $p_1$ 和 $p_2$ )。还描述了 $p_1$ 和 $p_2$ (蓝色虚线)之间的几何交叉产生的子代所能占据的目标输出和位置集合，其中 $o_1$ 代表该集合中的特定子代。图1.3 b 显示了由交叉(在这种情况下,由于适应度值表示已知输出和预测输出之间的误差,较低的值表示较好的解决方案)产生的可能后代的适应度函数。绿色点代表了 $o_1$ 的适应度值，在这个场景中， $o_1$ 在可能的后代中具有最好的适应度。正如我们所说，训练集中的每个实例对应语义空间中的一个维度。现在考虑，例如， $dim_1$ 是由一个实例诱导的，这个实例实际上是一个异常值。如果我们去掉这个实例，我们可以用简化的方式看到语义空间，其中只有 $dim_2$ 轴是重要的。在这种情况下，适应度函数将发生变化，变成图1.3 c 所表示的适应度函数，并且最佳的适应度值将不再等于 $o_1$ 的适应度。

图1.3：实例选择方法在适应度计算中的可能影响。

实例选择方法可以改变搜索过程的事实并不一定意味着找到的解会得到改善或者收敛速度会提高。我们提出猜想，这些改进可能是基于这样一个假设：在维数较低的语义空间上，如果这些维数是由相关的实例诱导的，那么依赖几何性质和操作的方法，如GSGP，可以利用在简化的搜索空间中工作的优势。但是，也存在一些可能的弊端。例如，如果实例选择方法删除了对搜索过程实际上至关重要的实例，那么一个重要的信息源就会丢失，得到的解决方案肯定会有缺陷。考虑到这一情景，我们的主要研究假设是：通过减少训练案例的数量，从而减少语义空间的维数，我们可以改进GSGP的搜索过程，使其更加简单和高效。

1.2 Objectives

为了验证我们的假设，本文主要关注以下研究问题：

在符号回归问题中，与GP相比，噪声数据对GSGP的性能有何影响?
维度的数量能够在多大程度上重塑语义空间，帮助搜索过程?
实例选择方法对GSGP执行的搜索结果有什么影响?
噪声数据对所提出的实例选择方法的性能有何影响?

为了回答Q1，我们对GSGP在噪声存在下的性能做了深入的分析。Q2通过分析实例选择方法对GP和GSGP的影响来解决。这样，我们就可以验证对搜索的改进是否可以与语义空间的一个更小的维度联系起来。Q3的答案是通过分析作为预处理步骤和作为集成的实例选择如何影响GSGP的预测能力来获得的。最后，Q4考察了在噪声存在的情况下，哪种实例选择方法表现更好。

1.3 Contributions

关于噪声数据对GSGP搜索的影响的研究： 在符号回归问题中，与GP相比，我们对噪声实例对GSGP性能的影响进行了分析研究。使用15个合成数据集，我们添加了不同比例的噪声，并将得到的结果与标准GP的结果进行了比较。两种方法的性能均使用传统的误差度量和从分类文献中改编的新的鲁棒性度量来衡量。本研究结果发表在 Miranda et al. [2017] 上。

Miranda, L. F., Oliveira, L. O. V. B., Martins, J. F. B. S., and Pappa, G. L. (2017). How noisy data affects geometric semantic genetic programming. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO ’17, pages 985–992, New York, NY, USA. ACM.

关于现有实例选择方法的研究和新策略的引入： 通过分析和扩展现有的实例选择方法，我们还研究了实例选择方法对GSGP的影响，所有这些都作为预处理步骤实现。我们通过使用多样化的真实数据集和合成数据集进行实验分析来验证我们的研究。我们还提出了一种新的方法，称为基于误差的概率实例选择，它允许在进化过程中通过选择实例来缩小语义空间，同时考虑每个实例对搜索的影响。本研究的初步结果发表在 Oliveira et al. [2016],，并提交给进化计算期刊，版本较为完整。

Arnaiz-González, Á., Blachnik, M., Kordos, M., and García-Osorio, C. (2016). Fusion of instance selection methods in regression tasks. Information Fusion, 30:69–79.

Arnaiz-González, A., Díez-Pastor, J. F., Rodríguez, J. J., and García-Osori, C. (2016). Instance selection for regression: Adapting drop. Neurocomputing, 201(Supplement C):66 – 81. ISSN 0925-2312.

1.4 Thesis Organization

本文余下部分结构安排如下：第2章介绍了语义遗传规划的主要概念，并详细介绍了本文要解决的问题。第3章介绍了相关工作，第4章分析了噪声数据对GP和GSGP的影响。第5章描述并评估了我们在语义GP中减少搜索空间大小的策略。最后，第六章对全文进行了总结，并对未来的工作进行了展望。

Chapter 2 Concepts and Problem Definition

本章在2.1节中讨论了进化算法的主要概念，以及遗传编程背后的特殊性。在2.2节中，还描述了与语义和几何语义遗传编程有关的基本要素。在第2.3节中，讨论了涉及实例选择任务的关键因素。在这一章中，我们介绍了评价指标，并详细介绍了我们试图解决的问题。

2.1 Genetic Programming

推动进化向前发展的三种主要机制是繁殖、突变和自然选择(也就是说,达尔文的适者生存原则)、[Raidl, 2005]。进化算法以一种简化的方式采用这些自然进化机制，以逐代改进代表给定优化问题 [Back and Schwefel, 1996]. 潜在解的种群个体的质量或适应度。

在遗传程序设计中，种群中的个体是可解释的程序，通常用语法树来表示。这个种群是通过反复选择最适合的程序并从中产生新的程序 [Langdon, 1996] 进化而来的。此外，种群规模通常是固定的，每一个新的程序都会替换一个现有的成员。通过在一组训练实例的输入属性上运行，并验证它们产生的输出与这些实例的实际输出值之间的接近程度，计算每个个体的适应度值。

图2.1给出了GP算法的传统步骤。它首先随机创建候选解的初始种群。然后，在每一代，基于适应度函数对种群成员进行评估，为其分配一个适应度，一些个体根据与其适应度成正比的概率进行选择，并提交给遗传算子。由此产生的个体替代当前种群，世代结束。该算法验证是否有一个停止准则满足(通常通过达到最大代数或找到满意解来实现)，并且在肯定的情况下，它停止执行并返回找到的最佳个体；否则，它就开始了新的一代。

遗传编程已成功应用于自动设计 [Nguyen et al., 2014]、模式识别 [Liu et al., 2016]、机器人控制 [Busch et al., 2002]、人工神经网络合成 [Ritchie et al., 2003]、生物信息学 [Langdon, 2015]、音乐 [Kunimatsu et al., 2015] 和图片生成 [Alsing, 2008] 等大量问题。我们在一种称为符号回归的特定类型的监督学习任务中使用GP，该任务涉及寻找一个数学表达式，以符号形式表示，它适合(或近似符合)的一组训练实例。与传统的线性和多项式回归方法将参数拟合为给定形式的方程不同，符号回归同时搜索参数和方程的形式 [Koza, 1992].

2.1.1 Representation and initialization

GP中个体表示结构的选择影响遗传算子的执行顺序、内存的使用和局部性以及遗传算子 [Banzhaf et al., 1998] 的应用。最常见的表达形式有线性结构、树结构和图结构。然而，这些结构在内存中实际持有的方式可能与它们被执行和修改的虚拟表示不同，以改善算法的一些与性能相关的方面。

从3种基本结构来看，语法树是GP中最常见的候选解表示形式。演化后的树由终端和功能集合中的元素组成。图1.1作为例子，给出了一个表示函数 $x^2 + 2x + 1$ 的语法树。程序 $(x, 1 和 2)$ 中的变量和常量组成的终端集是树的叶子，而算术运算子 $(+ 和 *)$ 是树的内部节点，构成函数集。

与其他进化算法类似，在GP中，初始种群的个体通常是随机产生的。有许多不同的方法来产生这种随机初始种群，但最常用和已知的是由Koza [ 1992 ]提出的，并被称为 grow, full and ramped half-and-half.

这三种方法都是以自顶向下的方式生成树，每次选择一个节点。完整的方法只选择函数，直到节点处于最大预定义树深度。然后它只选择终端。其结果是树的每一个分支都走向了全最大深度。反过来， the grow 包括生长形状可变的树，节点从函数中随机选择，终端集在整个树(除根节点外,它总是一个函数)中随机选择。一旦一个分支包含一个终端节点，那个分支就结束了，即使最大深度还没有达到。

The ramped half-and-half method 包括 both full and grow methods，并涉及使用深度参数创建相等数量的树木，其范围介于2和最大指定深度之间。例如，如果指定的最大深度为6，则有20 %的树木深度为2，20 %的树木深度为3，以此类推，直到深度为6。然后，对于每个深度值，一半的树是通过完全方法创建的，一半是通过生长方法生成的。

2.1.2 Individual Evaluation and Selection

决定选择哪些个体进行遗传操作的过程需要为每个新个体分配一个适应度值。一个个体所代表的解决方案越好，它就越有可能存活下来组成下一代。在符号回归情境中，我们感兴趣的是每个个体产生的输出，即从根节点开始评估其语法树时返回的值。在这种情况下，适应度函数可以被看作是捕获程序输出和一些已知的期望输出之间的差异(误差)的度量，通常由训练实例的输出值集合 [Krawiec and Pawlak, 2012]. 给出。

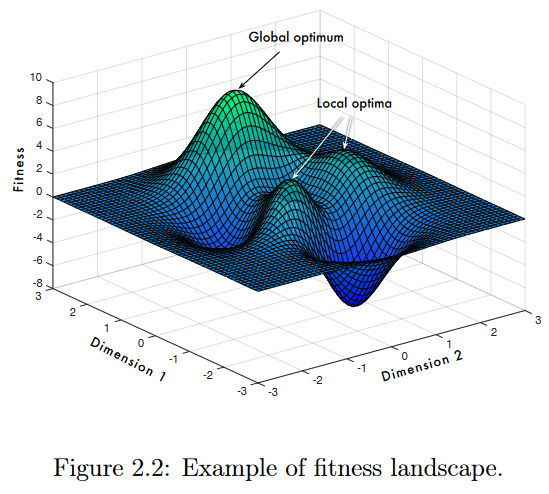
一个解的表示，称为基因型（genotype），其应用到问题中的用途或效果在逻辑上是分离的, 称为表型。在这个意义上，基因型编码了相应的表型，就像在自然界中，DNA编码了一个人类[Pawlak , 2015]的实际外观和操作。遗传编程与所有依赖于某种形式的进化适应的算法一样，都是在适应度景观的背景下运行的，它指的是从种群个体的基因型到其适应度的映射，并将该映射可视化[Kinnear, 1994]。在最简单的形式中，如图2.2所示的适应度景观可以被看作是一个图，其中水平方向上的每个点代表特定个体的基因型，其适应度被绘制为高度。如果基因型可以在两个维度上可视化，那么该图可以看成是一张三维图，其中可能包含丘陵和山谷，其顶点对应最优解的适应度值。

有许多不同的方法可以用于决定哪些个体将繁殖，哪些将从种群中移除。最常用的个体选择方法是锦标赛选择[Banzhaf et al., 1998]。本质上，该方法是以均匀概率从当前种群中随机选择k个个体组成的群体。选择该组内最优个体作为父代(或作为 parents 之一)进行下一步遗传操作。参数k称为锦标赛规模，可以用来修正方法(k值越高,选择高于平均质量的个体的压力就越大,这通常意味着更高的收敛速度) [Poli , 2005]施加的选择压力。

2.1.3 Genetic Operators

在GP中，初始化过程产生随机生成的个体通常意味着初始种群的平均适应度很低。因此，GP方法必须依赖搜索算子(也被称为遗传算子,在此背景下)，才能将搜索扩展到适应度景观[Oliveira, 2016]的高适应度区域。GP在这些算子 [Banzhaf et al., 1998] 的实现上与其他进化算法有很大的不同。虽然其中有很多，但通常只有三种，即交叉、变异和复制。

在交叉中，从两个父代中随机选择的子树进行交换，形成两个新的个体(子代)，如图2.3所示。其思想是在种群中积累对问题求解有用的构建块，交叉允许将它们聚集成更好的解[Koza , 1992]. 另一方面，变异算子通过挑选父代的随机子树并将其替换为新的随机生成的子树，仅创建一个子代，如图2.4所示。其思想是通过在种群中引入新的代码片段来给GP带来创新。因此，变异算子被用作多样性丧失和停滞的解决方法，特别是在小种群[ Pawlak , 2015]中。

图2.3：交叉算子的应用实例。虚线表示子树交换的点。

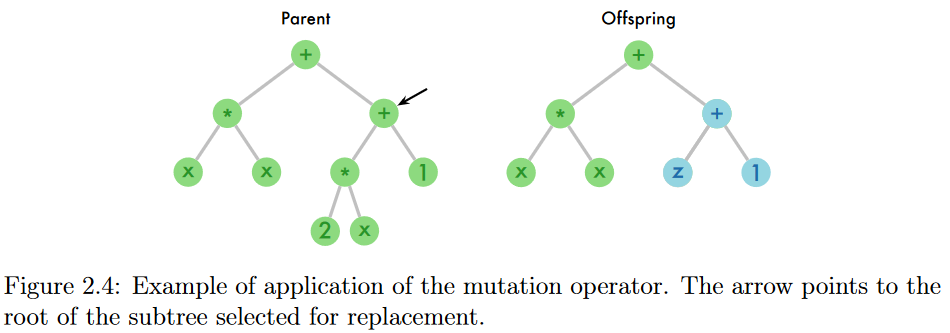
图2.4：变异算子的应用实例。箭头指向选择替换的子树的根。

GP中常用的第三种遗传算子称为繁殖。与其他算子不同的是，它不对所选择的父代进行任何修改，只需将父代简单地复制到下一个种群中，而不需要进行任何改变。

每个遗传算子的应用概率通常通过用户定义的参数来定义。交叉通常以高概率(90% ~ 95%之间)应用，而变异通常不应用或以极低概率(通常小于5%)应用。剩余概率，即完成100%，对应应用再生产算子[Poli et al , 2008]的概率。

2.2 Semantic GP

语义遗传编程( Semantic Genetic Programming，SGP )是遗传编程研究中一个较新的思路，起源于进化程序合成中基因型-表型映射的高度复杂性[Krawiec, 2016]。在其最初的定义中，GP只是在纯粹的句法层面操纵总体，从每个个体的语义(即行为)中抽象出来。这一方面使得它可以依赖简单的、通用的搜索操作符，但这种选择的主要后果是，很难预测程序中的修改将如何影响其语义[Vanneschi et al., 2014a]。因此，在GP中，即使对个体的结构进行微小的修改，也可能导致根本不同的行为，因此，标准遗传算子无法保证由它们生成的后代共享其父母的某些语义特征。

最近在GP领域的工作表明，程序的语义在的演化过程中可以起到至关重要的作用 [Vanneschi et al., 2014a]。为此，研究人员提出了多种利用语义感知的方法将搜索引导到搜索空间中更有前途的区域，从而提高获得更好解决方案的机会。

在GP文献中有不同的语义定义，例如，简约有序二元决策图( BDD ) [Beadle and Johnson, 2008] 和逻辑形式 [Johnson, 2007]。我们采用了一种与符号回归直接相关的语义定义。给定一个训练集 $T=\{(\mathbf{x}_i,y_i)\}_{i=1}^n$ 其中 $\mathrm{x} _i, y_i) \in \mathbb{R} ^d\times \mathbb{R}(i=1,2,\ldots,n)$ -一个代表程序p的个体的语义，记为 s§，定义为它应用于由T定义的输入集合时产生的输出的向量，即 $\mathbf{x} _1) , p( \mathbf{x} _2) , \ldots , p( \mathbf{x} _n) ] ^T.$

利用这个定义，个体的语义可以看成是n维语义空间中的一个点，其中n是训练实例(如图1.2所示)的个数。这种框架的优点之一是确定个体的语义本质上是 for free，因为每棵树都必须在训练实例上进行评估，以计算其适应度。然后，计算程序的语义是适应度计算的副作用，没有额外的计算成本 [Krawiec and Pawlak, 2013]。然而，更重要的是，这种对语义的理解将其与适应度函数紧密地绑定在一起，捕获了个体的输出与期望输出之间的差异。

2.2.1 GSGP

语义GP方法带来了一个新的视角，使得研究人员意识到提出程序合成任务的更深层次的含义是搜索具有某种语义的程序，而不是具有某种适应度函数的程序。GP中通常使用的适应度函数可以看作是 $S$ 中的一个度量，从而可以将集合 $S$ 形式化地转化为一个具有一定几何结构的空间，以用于搜索 [Krawiec, 2016].

以 $S$ 为度量空间，个体的适应度可以通过衡量其在 $S$ 中的表示与目标语义(t)之间的距离来确定，该距离由训练实例的实际输出值指定。这意味着，对于欧氏距离，例如，绘制关于S的评价函数的曲面具有锥的形式，其顶点对应于 $t$ ，如图2.5 a所示。

继语义空间概念之后，Moraglio et al. [2012] 提出了一个新的GP框架，该框架能够操纵个体在语义空间中的句法位置。该框架称为几何语义GP ( Geometric Semantic GP，GSGP )，直接在底层语义的空间中进行搜索, 诱导出如图2.5 a所示的单峰适应度景观。Moraglio [2011] 给出了正式的证据，证明了具有几何算子的进化算法可以优化锥景观，并且对几乎任何度量都有很好的结果。在实际应用中，GSGP引入了一类新的遗传算子，这些遗传算子作用于父代程序的语法，通过构造保证产生的子代程序满足一定的语义准则。

对于欧氏空间，几何语义交叉( Geometric Semantic Crossover，GSX )算子将两个父代结合起来，产生的一个子代表现为它们的凸组合，即对于任意输入，子代都位于父代之间的度量段中。这一特性保证了子代误差- -目标输出与个体产生的输出之间的散度- -被其父代最坏误差的下界所限制。对于基于曼哈顿距离的空间，由几何语义交叉产生的子代被放置在由其父代定义的超矩形内部。图2.5 b展示了GSX算子在使用欧氏距离定义的二维语义空间中的表示。

几何语义变异( GSM )算子通过对父代施加扰动生成子代，确保子代置于以父代p为中心、半径为ε [ Moraglio et al , 2012]的闭球 $B(p;\varepsilon)$ 内，其中 $\epsilon\in\mathbb{R}$ 与变异步长参数成正比。图2.5 c显示了GSM算子在二维语义空间中的表示，再次使用欧氏距离定义。

GSGP自提出以来，已成功应用于不同领域，如不同药代动力学参数的行为建模 [Vanneschi et al., 2013, 2014b]、高性能混凝土强度预测 [Castelli et al., 2013c]、涉及土地覆盖/土地利用应用的多分类 [Castelli et al., 2013b]、住宅建筑能源性能预测 [Castelli et al., 2015c]、能耗预测 [Castelli et al., 2015b,e]、森林火灾过火面积预测 [Castelli et al., 2015d] 以及海事意识应用 [Vanneschi et al., 2015]。

2.3 Instance Selection

在这一部分中，我们讨论了有关实例选择方法的关键因素。我们首先讨论了它们的优点和缺点，然后讨论了它们的划分和基本要素。虽然我们只关注这些方法在回归问题中的应用，但这里的讨论也可以扩展到分类问题中。同样，本部分所描述的大多数一般思想并不与特定类型的学习者联系在一起，这意味着，虽然在本文中，我们将实例选择过程与GSGP执行的回归结合在一起，但它们实际上可以被视为独立的主题。

简而言之，实例选择方法试图找到原始训练集T的一个子集S，使得|S| < |T|，并且由S诱导的模型的预测能力与由T诱导的模型的预测能力相似 [Arnaiz-González et al., 2016]。

在某种程度上，实例选择方法可以被认为是多目标问题：一方面，它们试图减少结果数据集的大小；另一方面，它们试图最小化某个误差度量[ Leyva et al , 2015b]。

实例选择方法的主要目标之一是加快学习过程。数据集规模的减少通常会导致处理所有训练实例和归纳模型所需时间的相应减少。也就是说，随着数据库的规模越来越大，实例选择方法的诱惑力也越来越强，这使得在合理的时间内得到结果是不可行的 [Leyva et al., 2015a].

然而，选择过程并不总是以与 performance-related 的问题为动机。在一些数据集中，输入空间的某些区域可能被过度覆盖，而另一些区域可能缺乏代表性。这可能导致由学习方法诱导的回归模型仅在这些过度表示的区域上表现良好，从而降低了它们的泛化能力。在这种情况下，从这些密集区域中移除实例可以通过引导回归模型考虑具有相似兴趣[ Cardie和Howe , 1997]的整个输入空间来改进诱导模型。

然而，在这项工作的背景下，实例选择方法最重要的好处是与GSGP执行的回归有关。正如我们所提到的，GSGP中的语义被定义为一个空间中的点，其维度与训练实例的数量相当。因此，通过减少实例的数量，我们自动降低了语义空间的维度数量，进而降低了搜索空间的复杂度。复杂度越小，可能的组合数量越少，可能会提高收敛到最优的速度。在本工作中，我们使用了两种策略来减少语义空间的维度数。第一种是在给定数据作为GSGP的输入之前应用的，只取决于数据集的特征。第二种策略依次考虑GSGP进化过程中每个实例的中值绝对误差来选择最合适的实例。

此外，还可以使用实例选择方法来降低存储需求，提高泛化性和准确性(当它被用来过滤原始数据集中的噪声时)。然而，尽管期望是获得一个等于或优于原始数据集的准确率，但在实践中这并不总是能够实现的- -即如果选择过程移除了对搜索过程实际上至关重要的实例，那么一个重要的信息源就会被浪费，一定的准确率损失可能是不可避免的 [Calvo-Zaragoza et al., 2015]。

根据选择子集的构建方式，实例选择方法可以分为增量式、减量式或批量式 [Arnaiz-González et al., 2016]。增量方法从空集开始，并向空集添加实例。实例在原始集合中的顺序对这些方法很重要，并将决定它们的有效性，因为当前实例的选择取决于已添加到集合中的实例。与之相反的方法是所谓的递减方法，它从原始数据集开始，并根据一定的标准删除他们认为"可废弃的"的实例。再次，顺序是重要的，但并不像增量方法那样重要，因为整个样本从一开始就可用来帮助做出决策。批处理方法依次标记正在进行的待淘汰候选实例, 一旦它们都被分析，它们就从数据集中移除。该技术保证了一个实例被淘汰后对完整子集的影响是已知的 [Wilson and Martinez, 2000].

区分实例约简技术的另一个方面是它们是否移除内部或边界实例 [Wilson and Martinez, 2000]。去除内部实例的想法是，它们不像边界实例那样影响学习过程，并且可以在对产生的回归模型影响相对较小的情况下被去除。我们利用这一思想并结合直觉，即如果学习器考虑的是具有相似重要性的整个输入空间，那么它可以更加准确，即我们寻求保留边界实例，同时删除输入空间中过度表示的区域的内部实例。侧重于消除边界实例的方法常被用来去除噪声。

还有一些方法应用加权函数来估计输入空间每个区域的相对重要性，以便在选择过程中考虑每个实例的影响。由于这是与本文提出的实例选择方法之一相关的一个关键方面，我们将在第5章对此进行更详细的讨论。

Chapter 3 Related Work

本章讨论了测量噪声对GP方法的影响和处理实例选择(IS)的现有策略。The first topic——噪声对GP的影响——通过分析两个方面来解决：(i)噪声数据的影响，GP Section 3.1.1其中我们提出了现有的策略，以减少噪声数据对GP搜索的影响；(ii)量化噪声鲁棒性的策略3.1.2节中，我们提出了一组度量，以估计由噪声实例引起的精度损失。关于第二个主题，在3.2节中，我们介绍了为处理分类上下文而构建的IS方法，以及将其用于处理回归任务的尝试。

3.1 Noise Impact

本部分重点介绍了在GP中为分析和最小化噪声数据的影响而进行的工作。此外，据我们所知，迄今为止，在符号回归问题的GP诱导模型中，还没有量化噪声影响的措施。因此，我们还概述了衡量噪声数据对分类技术性能影响的技术，这些技术我们适应于回归领域。

3.1.1 Genetic Programming with Noisy Data

在符号回归中已经提出了不同的策略来研究和最小化噪声数据对GP执行的搜索的影响。一方面，在进行回归之前，可以尝试过滤掉噪声数据, 另一方面，人们可以改进方法来简单地处理问题- -一种更普遍的方法。

遵循第一种策略 Sivapragasam et al. [2007] 在对短的两周河流流量时间序列进行符号回归之前，使用奇异谱分析(Singular Spectrum Analysis，SSA)过滤掉噪声成分。实验研究表明，当从短期和有噪声的时间序列中去除随机(噪声)成分时，可以改善短期预测。

关于尝试处理该问题的方法， Borrelli et al. [2006] 使用Pareto多目标GP对带有加性和乘性噪声的时间序列进行符号回归。作者采用了两种不同的配置，使用统计指标来实现适应度目标：(1)结合前两个矩的均方误差(MSE)；(2)加入峰度的偏度的MSE - -关于期望和评估输出计算的所有指标。对文献中50个函数生成的时间序列的实验分析表明，尽管多目标方法减少了过拟合和膨胀，但当噪声水平过高时，多目标方法并没有表现出良好的性能。然而，对于中等噪声水平，该方法可以成功地发现序列的趋势。

De Falco et al. [2007] 依次提出了两种以上下文无关文法为指导的GP方法，它们具有不同的适应度函数，考虑了吝啬和解的简单性。基于吝啬的适应度算法( PFA )和基于所罗门诺夫的适应度算法( SFA )分别采用基于吝啬思想的适应度函数和基于所罗门诺夫概率归纳的概念。这些方法在四个由已知函数生成的数据集上进行了比较，其中有五个不同程度的加性噪声。实验分析表明，与PFA相比，SFA在所有数据集和噪声水平下都具有更小的误差。

Imada and Ross [2008] 也提出了一个适合度函数，替代了基于误差和的函数，其中分数由目标值和评估值之间的标准化差异之和决定，考虑了不同的统计特征。对2个含2个水平加性噪声的数据集的实验分析表明，本文提出的适应度函数优于基于误差和的适应度。

尽管上述工作在符号回归的背景下处理了噪声，但在基于GP的回归方法中，缺乏直接量化噪声影响的研究。下一部分介绍了从机器学习文献中量化分类算法中噪声影响的措施。在第4章中，我们选择并调整这些指标来处理回归问题。

3.1.2 Quantifying Noise Robustness

当一种机器学习方法能够从数据中归纳出不受噪声影响的模型时，我们称其对噪声具有鲁棒性，即对噪声越鲁棒的方法，从有噪声和无噪声的数据[ S á ez等, 2016]中归纳出的模型越相似。

遵循这一前提，分类文献中的工作采用了在数据集中存在和不存在噪声的情况下比较模型性能的措施，以评估学习器的鲁棒性。在这里，我们介绍了其中的三个度量指标：相对风险偏差、相对准确性损失和均衡准确性损失。

相对风险偏差( RRB ) [ Kharin和Zhuk , 1994]衡量了最优决策规则的鲁棒性，即在训练数据没有"污染"的情况下，提供最小风险的贝叶斯决策规则。S á ez等人[ 2016 ]将该度量推广到任意分类器，由：

在这里插入图片描述

式中： $R_x \%$ 为分类器在噪声水平为 $x$ % 的数据集中得到的分类错误率，R为无噪声贝叶斯决策规则(这是一个理论上的决策规则,不是从数据中学习得到的,取决于数据生成过程)的分类错误率，定义为任意决策规则所能达到的最小期望误差。

相对精度损失( Relative Loss of Accuracy，RLA ) [ S á ez等, 2011]反过来量化了与没有噪声的情况相比，噪声水平的增加对分类器模型精度的影响。噪声水平等于x %的RLA测度定义为：

在这里插入图片描述

其中A0 %和Ax %分别是噪声水平为0 %和x %的分类器的准确率。RLA被认为比RRB更直观，因为在没有噪声( A0 % )的情况下获得高精度的方法将具有较低的RLA值。

最后，受Kharin和Zhuk [ 1994 ]度量的启发，提出了相等的Loss of Accuracy ( ELA ) [ S á ez等, 2016]作为RLA的修正，克服了RRB和RLA的局限性。初始性能( A0 % )在RLA方程中具有非常低的影响，与初始精度低的方法相比，具有高A0 %的方法的精度损失可以负向偏倚。例如，设A0 % = A10 % = 50为方法α的精度，A′0 % = 80和A′10 % = 75为方法α的精度方法的精度β。虽然方法β对10 %的噪声有很低的精度损失，但α分类器具有更好的RLA10 % -等于0。ELA测度由下式给出：
在这里插入图片描述
式中：Ax %和A0 %定义同式3.2。ELAx %等价于RLAx % + f ( A0 % ) - -参见S á ez等[ 2016 ]的推导- -其中因子f ( A0 % ) = ( 100 ~ A0 %) / A0 %等价于ELA0 %，仅取决于初始精度A0 %。因此，方法的ELAx %值是基于其鲁棒性，用RLAx %来衡量，并基于干净数据的行为- -即没有受控噪声- -用ELA0 %来衡量。

3.2 Instance Selection

用于分类任务的实例选择(instance selection，IS)方法种类繁多，各种调查也展示了当前最先进的技术[Olvera-López et al., 2010] 与回归问题类似，分类问题是用ML技术解决的，其中训练实例由一个输入向量和一个输出组成，但在分类中，输出是称为类的离散变量，而不是连续变量的值。

IS技术通常被用作预处理阶段，从训练集中选择- -有时甚至修改- -一组实例作为分类算法的输入。虽然实例选择可以用于不同的分类算法[Grochowski and Jankowski, 2004]，但它通常用于预处理k-最近邻(k-Nearest Neighbor，k-NN)算法 [Grochowski and Jankowski, 2004] 的训练集，这些工作的综述可以在[ Garcia et al . , 2012 ; Olvera-López et al , 2010 ; Cano et al , 2003]中找到

与用于分类任务的各种实例选择技术相比，用于回归问题的IS方法的数量相对较少。这种差异可以用后者相对于前者 [Kordos and Blachnik, 2012] 的复杂度增加来解释。例如，在回归问题中定义的实例的输出的连续性质允许系统预测无限多个可能的值，而在分类问题中，可能的结果的数量是有限的，由类的数量来定义。这两个任务之间的不相似性也阻碍了实例选择方法从回归域的分类的直接应用。尽管如此，文献中还有一些工作对分类问题的实例选择技术进行了一些调整，以便将其应用于回归领域。

用于回归的CNN (RegCNN)和用于回归的ENN (RegENN) [Kordos and Blachnik, 2012] 将用于分类问题中实例选择的密集最近邻(CNN) [Hart, 1968] 和编辑最近邻(ENN) [Wilson, 1972] 方法应用于回归领域。RegCNN和RegENN将其分类版本中使用的标签比较替换为基于误差的比较。RegCNN和RegENN不是通过比较k-NN分类器预测的标签和期望的标签来做出决策，而是通过比较回归方法预测的输出和期望的输出之间的误差到一个阈值，从而做出移除或保留一个实例的决策。

使用相同的阈值策略来适应两个版本的递减缩减优化程序(DROP) - -最初用于分类问题的实例选择- -回归任务 [Arnaiz-González et al., 2016]。作者还提出了DROP2和DROP3版本，其中分类模型正确分类的实例数由回归模型诱导的绝对误差之和代替。

RegCNN和RegENN方法在[Arnaiz-González et al., 2016]中被重新命名为Threshold ENN和Threshold CNN，并与一种离散化方法进行了比较，该方法将实例的连续输出转换为代表其标签的离散值，然后应用原始的ENN和CNN来选择实例。他们还使用Boosting集成技术将多个实例选择算法的输出进行组合，以选择最终的训练集。

回归类条件实例选择(CCISR) [ Rodriguez Fdez et al , 2013]将类条件实例选择方法从分类领域扩展到回归问题。CCISR使用类最近邻关系的修订版来计算用于从训练集中选择子集的实例打分函数。

另一方面，互信息(MI)原型选择 [Guillen et al., 2010] 从信息论领域获得灵感，而不是将IS方法从分类问题调整到回归问题。对于训练集中的每个实例，该方法计算不包含该实例的训练集的MI。如果一个实例的删除所引起的MI下降与它的一个邻居的删除所引起的MI下降相比并不显著，则该方法推断该实例并不重要，并将其删除。

简单多维迭代欠采样技术(Smits) [ Vladislavleva et al , 2010] 使用四种不同的度量标准之一- -邻近性、周围性、远程性和非线性偏差- -根据输入空间中的最近邻居来衡量实例的重要性。这些指标用于两种不同的方法：(i)生成用于适应度函数内部的权重，赋予每个实例对最终适应度值的不同重要性；(ii)从训练集中选择一个子集，由度量值最高的实例组成。

Chapter 4 Noise Impact

数据中噪声的存在是机器学习领域中经常出现的问题。噪声数据会严重影响机器学习技术的性能，导致过拟合和较差的数据泛化能力[Nettleton et al., 2010]。我们将噪声定义为模糊了问题 [Hickey, 1996] 的预测变量和目标变量之间关系的任何东西。在分类和回归问题中，噪声既可以出现在输入(预测)变量中，也可以出现在输出(目标)变量中，或者两者兼而有之，通常是数据生成过程中非系统误差的结果。

在过去的几年中，GSGP表现出了较强的鲁棒性和较高的泛化能力。研究人员认为这些特征可能与对噪声数据的敏感性较低有关。然而，目前还没有关于这一问题的系统研究。本章对GSGP在噪声环境下的性能进行了深入的分析。利用可以控制噪声的合成数据集，我们在数据中添加了不同比例的噪声，并将得到的结果与标准GP的结果进行了比较。

在回归问题的背景下，robust regression methods 已经被提出，以解决有噪声的数据点或异常值1，同时也处理大多数回归方法 do not respect [Rousseeuw and Leroy, 2005]的其他数据假设，如输入变量之间的独立性。尽管由于计算成本的原因，稳健回归在一段时间内并不受欢迎，但它为处理噪声提供了一种替代方法。在对遗传编程( Genetic Programming，GP )进行建模以解决符号回归问题时，仅有少数研究关注了噪声对数据泛化和过拟合结果的影响[Borrelli et al., 2006; Sivapragasam et al., 2007; De Falcoet al., 2007; Imada and Ross, 2008].

¹我们认为噪声点和离群点都是模式实例之外应该被识别的点。我们不去研究噪声点是否对任务实际有用的优点，并代表一个离群点。

相反，the community 已经非常关注复杂性、过拟合和泛化之间的关系，以及它与膨胀和简约 (bloat and parsimony) [Fitzgerald and Ryan, 2014; Vanneschi et al., 2010] 之间的关系。前者是指代码增长过度而适应度没有相应提高的现象，后者是指在函数集中只使用解决问题所需的函数的期望性质。这些的确是GP中与之密切相关的问题，但它们并不能说明不是GP搜索固有的问题，而是输入数据固有的问题。考虑到GP在输入数据中加入加性噪声时的表现，也有一些工作对此进行了研究 [Borrelli et al., 2006; Sivapragasam et al., 2007; De Falco et al., 2007; Imada and Ross, 2008].

如前所述，在本章中我们研究了噪声数据对GP和GSGP的影响。主要目的不是看标准GP如何处理噪声，而是研究与GP相比，考虑语义的GP如何处理该问题。我们首先在4.1.1节中描述了实验中使用的 the test bed。在4.1.2节中，我们概述了噪声对GSGP影响的研究现状。在4.1.3节中，我们分析了与GP相比，GSGP在不同噪声水平下的符号回归问题中的表现。

我们特别感兴趣的是在符号回归问题的输出变量中发现的噪声。这是因为GSGP操作在一个语义空间中，由训练集定义的输出向量引导。因此，输出中的噪声对GSGP中搜索过程的影响比预测变量中的噪声大得多。

4.1 Methodology

本部分介绍了分析GSGP在不同噪声水平的符号回归问题中与GP相比的表现的方法。我们介绍了我们研究中考虑的数据集，以及向数据中增量添加噪声的策略，以及我们采取的措施，以评估不同程度的噪声对GSGP和GP性能的影响。

4.1.1 Test Bed

由于真实世界的问题在从环境[Nettleton et al., 2010]获取数据并进行预处理时插入了固有噪声，我们采用了一个由合成数据组成的 test bed，该合成数据是从 [McDermott et al., 2012] 中提出的符号回归GP的基准候选列表中选出的15个已知函数生成的，然后根据一些质量标准从GP和GSGP文献中列举基准。

表4.1给出了构建数据集所采用的函数集和采样策略。训练集和测试集按照两种策略独立采样。 $U [a, b, c]$ 表示从区间 [ a , b] 中抽取的大小为 c 的均匀随机样本， $E [a 、 b 、 c]$ 表示以c为间隔均匀间隔的点的网格，从a到b，包括在内。对于前一种策略，我们生成了5组样本；对于后一种策略，由于过程是确定性的，我们只生成了一个样本。

在这里插入图片描述

为了评估噪声对GSGP和GP性能的影响，将训练实例的响应变量(期望输出)被一个具有零均值和酉标准差的加性高斯噪声扰动，并以r给出的概率施加。我们生成了r从0到0.2的数据集，步长为0.02，产生了11种不同程度的噪声，总共分析了165个数据集。

使用²给出的归一化均方根误差(Normalized Root Mean Square Error，NRMSE) [Keijzer, 2003; De Falco et al., 2007] 来衡量数据集中方法的性能：

在这里插入图片描述
其中 $\bar{t}$ 和 $\sigma_t$ 分别是目标输出向量 $t$ 和 $f$ 的均值和标准差，是由回归方法导出的模型(函数)。当模型等价于 $\bar{t}$ 时，NRMSE等于1；当模型完美拟合数据时，NRMSE等于0。我们使用标准化版本的RMSE，以便能够以公平的方式比较来自不同噪声水平和数据集的结果，如下一部分所述。

4.1.2 Noise Robustness in Regression

GSGP和GP在具有不同噪声水平的同一数据集中的性能通过第3.1. 2节中提出的适应于回归域的鲁棒性度量，即RLA和ELA进行评估。而不是使用分类方法的性能度量- -准确率- -我们采用了NRMSE。

值得注意的是，准确度定义在[0%、100%] -或[0、1] -，其值越高，意味着准确度越高，因此，误差越小。因此，RLA或ELA测量值越大，该方法对各自噪声水平的鲁棒性越差。另一方面，NRMSE定义在[0，+∞)，取值越高，误差越大。

在此背景下，我们引入相对误差增加( Relative Increase in Error，RIE )和相等的增加误差(相等的Increase in Error，EIE )度量分别作为RLA和ELA的替代，来量化回归域中的噪声鲁棒性。RIE和EIE分别由方程4.2和4.3给出，其中 $E_x$ %是模型在含 $x$ %噪声的数据集上得到的NRMSE。 $E_0$ %为模型在没有噪声的数据集中得到的NRMSE，并且在两个分母中加入一个加一项，以避免除以零。这两个测度的值越高，说明模型对各自的噪声水平越敏感。
在这里插入图片描述

类似于ELA，我们可以根据方程4.4推导出EIE，使得 $EIE_x$ %等于 $RIE_x$ %加上一个仅依赖于模型NRMSE而没有噪声的项 $EIE_0$ %。

在这里插入图片描述

4.1.3 Experimental Analysis

本部分对GSGP在带噪声数据的符号回归问题中的性能进行了实验分析。我们使用4.1.2节中介绍的噪声鲁棒性度量和表4.1中提出的15个数据集，在11个不同的噪声水平下，将结果与标准GP [Banzhaf et al., 1998] 进行了比较。考虑到GSGP和GP的非确定性，每个实验重复50次。如第4.1.1节所述，我们对均匀策略随机获得的数据进行了五次重采样。在该采样策略的数据集中，每个样本重复10次实验，共50次重复。

所有的执行使用了一个由1000个个体进化了2000代的种群，GP和GSGP的锦标赛选择分别为7和10。采用生长法生成几何语义算子内部的随机函数，采用 ramped half-and-half method 生成初始种群，两者最大个体深度均为 6。终端集包括每个数据集的输入变量和从区间[- 1、1]中随机挑选的常数值。该函数集包括3个二元算术算子(+ , - , ×)和一个解析商(AQ) [ Ni et al , 2013]，它是算术除法的一种替代，具有相似的性质，但没有不连续性，由下式给出：
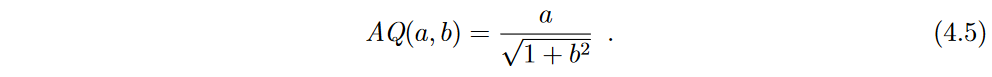
在这里插入图片描述
对于GP，交叉概率和变异概率分别定义为0.9和0.1。对于GSGP，我们采用了基于曼哈顿的适应度函数的交叉和[Castelli et al., 2015a]的变异算子，两者的概率均为0.5。变异算子所需的变异步长定义为训练数据给出的输出( Y )的标准差的10%。

尽管在实际场景中，训练数据和测试数据中都存在噪声，但在这个控制实验中，我们只在训练集中添加了噪声。虽然这个决定最初可能看起来是不合理的，但它的动机是，为了衡量GP方法生成的模型在噪声存在的情况下是否有效，我们必须验证它在没有噪声(也就是说,如果它产生的模型可以逼近原始函数的曲线,而不管它是在有噪声的情况下训练的)的情况下如何工作。如果在测试集中插入噪声，良好的结果可以表明模型学习到了由训练集和测试集表示的曲线的噪声区域。

由于这个决定，训练值和测试值不能互相比较(这并不是一个问题,因为我们专注于比较GP和GSGP的测试结果)。这就是为什么总体上呈现的测试误差小于训练误差的原因。为了研究这一方面，我们进行了不同的实验，其中我们还在测试集上插入了噪声。例如，对于10%的噪声水平，8个数据中有7个数据的训练误差小于测试误差。

图4.1显示了当增加噪声实例的百分比时，中值训练和测试NRMSE是如何受到影响的。对于无噪声数据的结果，除 keijzer-6 and vladislavleva-5 两个数据集外，GSGP在所有数据集上都表现出更好的中位数检验NRMSE。然而，当噪声水平大于或等于18% keijzer-1，6% keijzer-1，2% (vladislavleva-1)和 14% vladislavleva-4时，观察到相反的行为。此外，当数据集keijzer-2, keijzer-3, keijzer-4, keijzer-7, keijzer-8, vladislavleva-2 and vladislavleva-8 的噪声水平增加时，GSGP测试NRMSE与GP近似。这种行为可能表明，尽管在大多数数据集中，GSGP在低噪声水平下的性能优于GP，但当噪声水平增加时，其性能恶化的速度比GP更快。值得注意的是，无论两种方法在测试数据中的表现如何，在所有实验中GSGP的训练中值NRMSE都小于GP的训练中值NRMSE，这可能表明GSGP比GP有更大的倾向于过拟合噪声数据。

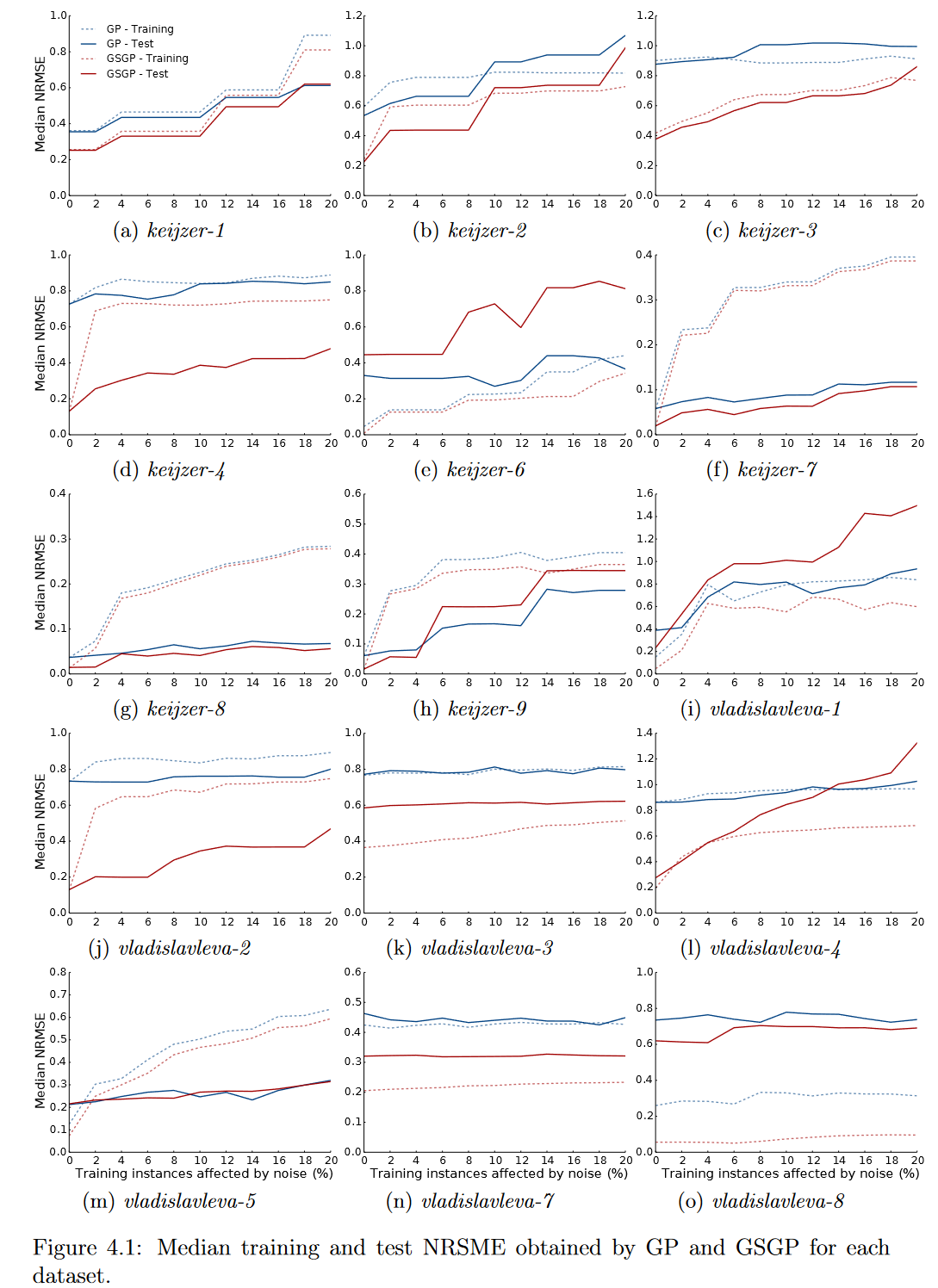
在这里插入图片描述
图4.1：GP和GSGP对每个数据集得到的NRSME进行中位数训练和测试。

图4.2依次显示了4.1.2节中提出的EIE和RIE度量的中值，由GSGP和GP方法在仅考虑测试集的不同噪声水平下获得。在分析RIE值时，我们验证了在10个数据集keijzer-4, keijzer-6, keijzer-7, keijzer-9, vladislavleva-1, vladislavleva-2, vladislavleva-4 and vladislavleva-7中的所有噪声水平下，GSGP比GP对噪声的鲁棒性更低。对于噪声水平大于等于4%的 keijzer-1 和 keijzer-8 以及数据集 vladislavleva-8. 中的6%。

在这里插入图片描述

然而，当我们观察EIE的值时，这种情况发生了变化。在6个数据集keijzer-4, keijzer-7, keijzer8, vladislavleva-2, vladislavleva-3 and vladislavleva-7中，GSGP在所有噪声水平下都比GP更鲁棒，而在2个数据集 keijzer-6 and vladislavleva-1 中则相反。此外，在数据集凯泽- 1和凯泽- 3中，当噪声水平小于18 %时，GSGP比GP获得更小的EIE值。另一方面，在数据集凯泽- 9和vladislavleva - 4中，当噪声水平大于4 %时，GP在EIE方面优于GSGP。这些分析表明，总体而言，根据EIE测度，GSGP比GP对噪声更加鲁棒。

产生这些矛盾结果的主要原因在于这些措施对于量化噪声鲁棒性的重要性。如4.1.2节所示，在无噪声数据集中，方法性能在RLA测度中的影响非常低，从而在其回归对应物( RIE )中的影响也非常低。另一方面，ELA和EIE在各自的方程中加入一个项来表示模型在无控制噪声数据中的行为。由于在没有噪声的情况下，GSGP在大多数场景中的表现优于GP，因此EIE认为它比RIE对噪声更鲁棒是很自然的。

为了比较图4.1和图4.2中的结果，我们进行了三个配对的单尾Wilcoxon检验，比较GP和GSGP，在原假设下，它们的中位数表现- -在所有数据集的中位数检验NRMSE，RIE和EIE - -是相等的。根据图4.1和4.2所示的总体结果，所采用的备选假设有所不同：GSGP在NRMSE和EIE方面优于GP，GP在RIE方面优于GSGP。试验报告的p值见表4.2。在95%的置信水平下，符号表示没有放弃原假设，符号N(H)表示GSGP在统计上优于(差于) GP。对于NMRSE测度，GSGP在噪声为 0%, 2%, 4%, 6%, 8% and 12% 的数据集上优于GP。然而，当噪声水平大于12%时，GSGP和GP之间没有统计学差异，这表明GSGP的性能接近于GP。在分析鲁棒性度量时，RIE表明，在所有噪声水平下，GP比GSGP具有更强的鲁棒性。然而，EIE测度的结果并非如此，这表明在噪声水平( 2%和4%)较低的情况下，GSGP比GP更稳健，并且在噪声水平大于4%的情况下没有显著差异。

在这里插入图片描述

总之，这些结果表明当使用RIE措施来分析结果时, GP比GSGP对所有级别的噪声都具有更强的鲁棒性. 另一方面，当分析NRMSE或EIE值时，GSGP在对较低水平噪声的鲁棒性方面优于GP，而在较高水平噪声中，GP没有显著差异。因此，虽然GSGP在较低的噪声水平下表现优于GP，但对于较大的噪声水平，两种方法往往表现相当。

Chapter 5 Instance Selection for Regression

正如我们所提到的，当GSGP用于符号回归时，任何个体的语义都可以表示为n维语义空间中的点。现实应用中使用的大多数数据集包含相当数量的实例，这意味着搜索发生在高维语义空间中，复杂且通常难以处理。在这种背景下，我们通过减少输入实例的数量来自动降低维度的数量和搜索空间的复杂度。直觉上，与搜索空间相关的较低复杂度可以导致增强的回归模型。

对于规范GP框架，这种关于语义空间复杂性的论证并不适用- - GP所采用的规范遗传算子并不能保证语义空间中的任何几何性质。然而，根据数据集的不同，许多实例可能代表同一信息- -例如输入空间的特定区域。因此，通过从该空间的过度代表区域中移除实例，我们可以在不显著恶化回归模型质量的情况下减少执行时间。同样，这种潜在的好处也延伸到了GSGP。

本章提出了我们的方法，通过实例选择方法的应用来探索和评估降低语义空间维度数量的影响。

我们首先介绍了在本文的后面部分使用的数据实例的标记。给定输入训练集 $T=\{(\mathbf{x}_i,y_i)\}_{i=1}^n$ ，其中 $(\mathrm{x} _i, y_i) \in \mathbb{R} ^d\times \mathbb{R}$ 和 $\mathrm{~x_i= [ x_{i1}, x_{i2}, \ldots , x_{id}] , ~for~}i= \{ 1, 2, \ldots , n\}$ ，我们定义 $\mathbf{x} _1, \mathbf{x} _2, \ldots , \mathbf{x} _n] ^T$ 和 $Y=[y_1,y_2,\ldots,y_n]^T$ 分别为 $n\times d$ 的输入矩阵和n元输出向量。两个实例在输入空间中的距离 $I_i，I_j$ 为

其中 $u||_p$ 表示给定向量 $\mathbf{u}\in\mathbb{R}^{d}$ 的输入空间中的p-范数，定义为：

该距离用于计算给定实例 $I_i=(\mathbf{x}_i,y_i)$ — $N_i=\{n_{i1},n_{i2},...,n_{ik}\}$ -的k个最近邻点的集合，以及它的关联集合 $A_i= \{ I_j|I_i\in N_j for j\in \{ 1, 2, \ldots , n\} ~and~ i \neq j\}$ -即在它们的k个最近邻点中具有 $I_i$ 的实例。

本章的结构如下：首先，在5.1节中，我们描述了我们的思路和利用现有的实例选择预处理策略的特殊方式。在5.2节中，我们介绍了一种新的集成IS方法，称为基于误差的概率实例选择(PSE)，它根据实例的中值绝对误差来选择实例。在5.3节中，我们对本章所讨论的IS策略进行了实验分析，并将其应用于一组真实数据集和合成数据集，并讨论了所获得的结果。最后，在5.4节中，我们验证了PSE方法是否也能在噪声场景下提供良好的结果。

5.1 Pre-Processing Strategies

在这一部分，我们探讨了作为预处理步骤的IS策略。我们首先在5.1.1节中描述了3.2节中提出的方法TCNN和TENN。这些方法遵循了用于分类领域的IS方法中使用的相同思想，但进行了调整，以便它们能够处理回归任务。在5.1.2节中，我们探讨了实例加权的思想，作为一种根据实例重要性来区分实例的方法。我们还探索了与输入空间相关的降维技术，以产生低维嵌入作为增强实例之间紧密度的一种尝试。

5.1.1 TENN and TCNN

如前所述，阈值编辑最近邻(TENN)和阈值压缩最近邻(TCNN) [Kordos and Blachnik, 2012] 适应分类问题的实例选择算法- -编辑最近邻(ENN) [Wil-son, 1972]. 和压缩最近邻(Condensed Nearest Neighbor，CNN) [Hart, 1968]- -分别到回归域。它们在算法1和算法2中给出。

这些算法根据基于相似度的误差，采用内部回归(internal regression method)的方法对实例进行评估。从训练集中保留或移除第 $i$ 个实例的决策是基于实例预测 $\hat{y}_i$ 和期望输出 $y_i$ 的偏差，由 $|\hat{y} _i- y_i|$ 给出。如果这个差值小于一个阈值 $\theta$ ，则 $\hat{y}_i$ 和 $y_i$ 被认为是相似的，根据算法的不同，该实例被接受或拒绝。阈值θ根据数据集的局部特性计算，由 $\alpha\cdot sd(N)$ 给出，其中 $\alpha$ 是控制灵敏度的参数， $s d (N)$ 返回由实例的k个最近邻组成的集合N的输出的标准差。

TCNN和TENN采用的内部回归方法(internal regression method)- -算法1和2中提出的过程回归- -可以被任何回归方法所取代。我们的实现使用版本为kNN (k-nearest neighbor)的算法进行回归来推断( $\hat{y}$ )的值。除了训练集T外，这些算法还接收待考虑的邻居数和一个参数α作为输入，它控制着如何计算阈值。最后，返回用于训练外部回归方法的实例集合P。

TENN是一种递减的方法，从集合P中的所有训练案例开始，迭代地移除偏离其邻域的实例。一个实例 $(\mathbf{x}_i,y_i)$ 被认为是 divergent，如果没有该实例学习的模型推断的输出( $\hat{y}$ )与其输出( $y_i)$ )是不相似的。另一方面，TCNN是一种增量式的方法，从P中的训练集中仅有一个实例开始，并迭代地只添加那些可以改善搜索的实例。只有当P学习到的模型推断的输出( $\hat{y}$ )偏离 $y_i$ 时，才添加实例( $(\mathrm{x}_i,y_i)$ )。

5.1.2 Instance Weighting

本节介绍一种方法，该方法基于输入空间中实例的集中程度对回归方法执行的训练阶段有至关重要的影响这一假设，包括基于GP的方法。这个假设来自于一个事实，用于指导GP执行的搜索的错误度量对每个实例赋予相同的权重。因此，具有较高实例浓度的输入空间的区域偏向于搜索，因为适应度函数对在这些密集区域上具有良好性能的个体给予了更好的奖励。

图5.1给出了这样一个行为的例子。考虑一个由60个均匀分布在输入空间[ -1.5 , 4.5]中的点组成的训练集T，其输出由方程5.3定义，表示为图中的圆(充满和空洞)。值得注意的是，区间[-1.5, - 0.5]和[1, 4.5]虽然在输入空间中具有相同的实例分布，但与区间(0.5, 1 )相比，在输出空间中具有更密集的分布。为了使输出空间中的分布更加均衡，我们从T中选取子集S，用填充圆来表示。红色和蓝色曲线分别代表使用T和S作为训练集的GP诱导的函数。红色曲线在稠密区域收敛到一个使误差最小化的常数，而蓝色曲线能够捕获原始函数的趋势。

图5.1：不平衡数据集示例及实例选择方法对回归的影响。

5.1.2.1 Weighting Process

Vladislavleva et al. [2010] 提出了四种不同的度量方法来估计训练数据集中每个实例的重要性。 Harmeling et al. [2006] 提出的 The proximity and surrounding metrics 分别度量了给定实例的邻居之间的 the degree of isolation and the degree of spread。反过来，the nonlinearity metric 是基于通过k个最近邻的最小二乘超平面的偏差。最后，the remoteness metric 是 the proximity and surrounding metrics. 的组合。

The proximity function γ 试图通过测量一个实例到它的k个最近邻的平均距离来估计它是多么的孤立：

然而，the proximity function 没有考虑实例与其邻居之间的相对方向。因此，类似于图5.2所描述的情况是无法区分的。这种信息可以通过测量从 $I_i$ 到它的k个最近邻点的向量的平均长度来捕获，该函数δ试图识别位于响应面边缘的实例- -即不均匀地被它的邻居包围的实例：

图5.2：由于周围函数也考虑到了邻居的方向，当邻居位于同一方向时，周围函数赋予了更高的权重值。

5.1.2.2 Input Space Dimensionality Reduction

在现实应用中使用的大多数数据集- -以及在我们的实验中使用的数据集- -代表了一个复杂的高维输入空间。在最后一节中提出的权重函数严重依赖于每个实例与其最近邻之间的紧密度的概念，这在高维空间中可能是欺骗的。为了减轻这个潜在的问题，以及获得一些关于数据集的见解，我们将降维技术 作为实例选择过程中的步骤之一。

降维方法允许我们将高维数据集转换为二维或三维映射，低维表示中的实例之间的距离尽可能地反映了高维数据集中实例之间的相似性。理想情况下，这样的方法可以让我们观察到数据的许多潜在结构，并了解实例是如何在原始输入空间中排列的。

通过在我们的实例选择过程中结合降维方法，我们期望增强实例之间邻接关系的感知，最终提高权重函数产生的值的显著性。

我们将所有包含4个或4个以上属性的数据集的输入属性通过以下降维技术嵌入到二维输入空间中：

主成分分析( Principal Component Analysis，PCA) [Hotelling, 1933]：利用正交变换将一组可能相关变量的观测值转换为一组线性不相关变量的值，称为主成分。
Isomap Mapping [Tenenbaum et al., 2000]：寻找一个低维嵌入来保持所有点之间的测地距离。
多维尺度分析( Multi-dimensional Scaling，MDS ) [Torgerson, 1952; Borg and Groenen, 1997]：寻求数据的低维表示，其中的距离很好地尊重了原始高维空间中的距离。
t-分布随机邻域嵌入(t-SNE) [Maaten and Hinton, 2008]：将数据点的相似度转换为概率。原始空间中的亲和力用高斯联合概率表示，嵌入空间中的亲和力用 Student’s t-distributions. 表示。

图5.5展示了 energy-cooling dataset- -我们在实验中使用的数据集之一- -在应用4种降维技术后的一种表示方式。

通过将降维方法应用于数据集 energy-heating 的其中一个训练折叠上创建的投影和嵌入，其中组件的数量设置为2。

5.1.2.3 Selection process

我们采用了算法3中提出的基于SMITS过程[Vladislavleva et al , 2010]的实例选择方法。它以一个训练集T、一个加权函数和一些控制变量为参数，输出一组实例S，并根据它们的信息含量进行选择。该算法开始于测量T中每对实例之间的距离，即第二行。值得注意的是，这些距离只考虑输入空间，因为如果我们还包括输出空间，它们之间的接近可能会被误导。在第3 - 6行中，算法为每个实例建立它们的初始邻居集和关联集。然后，在第7 - 10行中，它衡量了整个数据集。当我们使用邻近、周围或非线性函数时，这是一个相当直观的过程。而对于距离函数，则需要执行一个归一化步骤，并增加一个参数m。这个参数表明，如果组合方法应该是有序的，如公式5.7所定义的，或者组合权重应该通过简单地取邻近权重和周围权重之间的平均值来计算。在12-17行中，算法迭代地对整个数据集进行排名。它通过寻找权重最低的实例并将其注册在一个排序数组中开始每次迭代。此后，该实例不得不被忽略，这是由将其权重设置为∞所迫。之后，算法更新其k个最近邻(第16行)中存在Il的实例的权重。该算法在第18行创建具有所选实例的集合S后终止，该集合是根据创建的排序从T中选择一个实例子集完成的。子集的大小由参数s来定义。

图5.6展示了实例选择过程应用于Kotanchek数据集的结果。图5.3a中所示为相同的响应面，但是，使用5.1. 2.1节中给出的权重函数删除了25%的实例。

图5.6：实例选择过程应用于kotanchek数据集的结果。每个图表示相同的响应面，见图5.3 a，但使用四个权重函数中的一个删除了25%的实例。对于所有的执行，邻域大小设置为4。

我们实现SMITS过程所花费时间取决于每个实例的实例数 $n$ 、维度数 $d$ 和邻居数 $k$ 。在算法3的第4行，我们计算了距离矩阵，这需要 $O(n^2d )$ 次运算。The proximity and surrounding functions 需要所有的 $k$ 个邻居，如果我们对邻居进行排序，可以在 $O (kn)$ (在期望线性时间内使用 $k$ 次选择)或 $O (n l o g n)$ 中找到。在我们的实现中，我们选择了后一种方法，因为考虑到通常会使用较大的 $k$ 值。因此，the proximity and surrounding functions 的复杂性为 $O( n^2d + n^2max ( k , log n )))$ 。

对于 the nonlinearity function，确定逼近 $k$ 近邻的平面的过程需要求解 $k$ 个线性方程组，这使得非线性函数的复杂度等于 $O(nk^3)$ 。

5.2 PSE

迄今为止提出的方法都忽略了外部回归算法的任何信息，因为它们都是在预处理阶段使用的。为了克服这一限制，我们提出了一种基于中值绝对误差的实例选择方法，该方法考虑了当前种群中程序的输出。该方法称为基于误差的概率实例选择(PSE)，每隔ρ代从原始训练集中概率地选择一个子集，如算法4所示。中值绝对误差越大，则一个实例被选中组成GSGP使用的训练子集的概率越高。该方法的基本原理是对那些在理论上更难被GSGP演化的当前种群所预测的实例赋予更高的概率。

给定一个GSGP总体 $P=\{p_1,p_2,\ldots,p_m\}$ ，第 $i$ 个实例 $(\mathbf{x}_i,y_i)\in T$ 的中值绝对误差由集合 $E=\{|p_1(\mathbf{x}_i)-$ $y_i|,|p_2(\mathbf{x}_i)-y_i|,\ldots,|p_m(\mathbf{x}_i)-y_i|\}$ 的中值给出.利用这些值对T进行降序排序，并利用实例在T中的位置计算其被选入训练集的概率。

为了计算这个概率，该方法将实例在T中的排序归一化到[ 0、1 ] by的范围内
在这里插入图片描述
其中 $i$ 是实例在有序集T中的位置，|.| 表示集合的基数， $\tilde{r}∈[0、1]$ 是规范化秩. $\tilde{r}$ 的值用于计算选择实例的概率，由

其中λ是一个确定概率函数下界的参数. λ值越高，选择的实例越多。该函数下的面积相当于 $\frac{2+\lambda}3$ ,，对应于从T中选择的实例比例。图5.7以λ = 0.3为例，根据" r "给出了问题的值。由此得到的实例数与曲线下面积(图中的阴影区域)成正比，相当于2 + λ 3。

## 5.3 Experimental Analysis 在这一部分中，我们对应用于各种真实世界和合成数据集的实例选择方法进行了实验分析。本质上，我们的目标是分析GSGP的预测能力如何受到本章迄今为止提出的实例选择方法的影响。我们首先在5.3.1节介绍了实验中采用的实验设计。在5.3.2节中，我们用TCNN和TENN进行实例选择来评估GSGP得到的结果。在5.3.3节中，我们对GP和GSGP中的权重函数和输入空间降维的效果进行了推理，并对它们进行了对比，以分离语义空间降维的影响。最后，在5.3.4节中，我们通过讨论PSE获得的性能来结束我们的实验分析。

5.3.1 Experimental Design

我们使用了一组从UCI机器学习库[Lichman, 2015]中选取的15个数据集，GP基准测试集[McDermott et al., 2012]和文献[Albinati et al., 2015; Chen et al., 2017]中的GP研究进行了实验，如表5.1所示。我们根据数据集的性质和来源为实验定义了不同的策略，详见表5.1的最后一列。对于真实数据集，我们将数据随机划分为5个相同大小的不相交集合，并使用5折交叉验证(10 × 5 - CV)执行方法10次。对于人工合成的数据集，我们根据其原始工作中定义数据集的方式，采用了两种不同的策略：对 non-deterministic sampling functions 生成的数据集重采样5次，每次采样(10 × 5-ND)重复实验10次；采用 deterministically sampled 的数据集，以相同的数据覆盖率(50 × D)重复进行了50次实验。采用相同的策略对训练集和测试集进行采样。唯一的例外是Vladislavleva - 1数据集，其中训练集按照10个5-ND策略(10 × 5-ND)进行采样，测试集按照原实验[McDermott et al., 2012]只进行一次确定性采样。最终，所有方法都执行了50次。

我们采用配对Wilcoxon检验来分析在该 test bed[Demšar, 2006] 上进行的实验结果的统计学差异。我们采用R语言的stats包提供的Wilcoxon检验，并进行连续性校正和精确p值计算[R Core Team, 2015]。对于所有这些测试，我们认为置信水平为95%。

本节实验采用的参数配置与4.1.3节相同，只是代数不同，本例中GP和GSGP均设置为250代。我们使用均方根误差(RMSE)作为适应度函数。

5.3.2 TCNN and TENN

在这一部分中，我们比较了在进化阶段(预处理)之前进行实例选择和不进行实例选择的GSGP所获得的结果，使用TCNN (GSGP-TCNN )和TENN (GSGP-TENN )方法，对α分别在区间[0.1,1]和[5、5、10]中平均分配10个不同的值，并在初步实验中测试了一系列值后采用k = 9。表5.2给出了训练和测试的RMSE的中位数和用α得到的数据缩减，使得TCNN和TENN方法的数据缩减最大，分别为1和5.5。

表5.2：每个数据集的算法实现的中位数训练和测试RMSE和减少(%red.)。根据Wilcoxon检验，在95%的置信度下，黑体高亮显示的值对应于检验RMSE静态地比GSGP得到的值差。

为了研究实例选择方法在GSGP中的重要性，我们将其与第三种策略进行了比较，其中我们从每个数据集中随机选择 $l$ 个实例，不进行替换，以组成新的训练集，作为GSGP的输入。 $l$ 的值被定义为由TENN和TCNN产生的集合的最小尺寸。表5.2给出了这些实验在最后两列(记为’ GSGP-Rnd ')的训练和测试RMSE的中位数。得到的结果表明，使用TCNN和TENN并没有对GSGP结果进行系统性的改进。而且，它们得到的结果并不比随机产生的结果好.因此，这些方法所使用的策略似乎并不适合我们所拥有的情景。

5.3.3 Instance Weighting

在这一部分中，我们对5.1.2节中描述的实例选择方法进行了实验分析。我们的主要目标是分析GP和GSGP的预测能力是如何被作为预处理步骤的实例选择所影响的，当使用所提出的权重函数和嵌入创建方法时。

5.3.3.1 Parameter Tuning

为了避免属性值范围的差异导致数据加权过程偏向于高范围属性，我们将test bed中所有数据集的输入和输出值缩放到区间[0、1]。然而，值得注意的是，尽管这些比例值被实例选择方法用来决定保留哪些实例，但最终得到的子集总是由原始训练实例组成。

我们进行了初步的实验，以确定加权函数应该使用哪个邻域大小(k)。除了常量之外，我们还包括相对于每个数据集的实例数和属性数的值。这些实验使用表5.1中列出的相同数据集执行，并表明当考虑所有数据集和邻近、周边和远程功能时，值5提供了最佳结果。非线性函数需要确定一个唯一的超平面，该超平面尽可能地靠近每个实例的邻居集，要求邻域大小至少与属性个数成正比。因此，在本节的实验中，我们在使用非线性函数时采用属性个数作为邻域大小，在使用其他任何函数时采用5作为邻域大小。

我们还分析了用于寻找最近邻居的距离函数如何影响实例选择过程。对于式(5.1)和式(5.2)中使用的参数p，我们采用了4种配置：p=1和p=2，分别对应曼哈顿距离和欧氏距离；p=0.1和p=0.5，一般称为分数距离(实际上,当p < 1时,我们不能把它看成是一个距离函数,因为它违反了三角等式)。所有实验均在4种构型下进行。根据Vladislavleva等人[2010]的观点，当数据集的维数较大时，应该使用分数距离度量来寻找最近邻。然而，我们的实验并没有证实这一假设，

对于属性个数大于100的数据集。为了避免不必要的广泛性，我们在本节中只给出了关于欧氏距离的结果，从而得到了最好的结果。

5.3.3.2 Experimental results - GP

在定义邻域大小和距离度量的基础上，重点研究实例选择过程对GP和GSGP搜索的影响。为了量化这种影响，我们采用两个指标：测试均方根误差(test RMSE) - -衡量回归模型产生的误差和执行时间，因为加权过程增加了计算复杂度。

我们首先讨论了GP得到的结果。对于每个数据集，除了从训练集中移除的实例数量，我们给算法提供了相同的参数集，这导致训练集的大小相对于它们的原始大小从75%到99%不等。例如，对于 keijzer-6 and parkinsons datasets- -我们测试平台中最小的数据集和最大的数据集- -这些选择因子分别对应于从1到13和从59到1469不等的删除实例。

我们使用上一部分提出的四种加权函数构建的子集进行了实验：proximity, surrounding, remoteness, and nonlinearity 。表5.3、5.4、5.5和5.6分别给出了这些实验对应的中位数检验均方根误差。

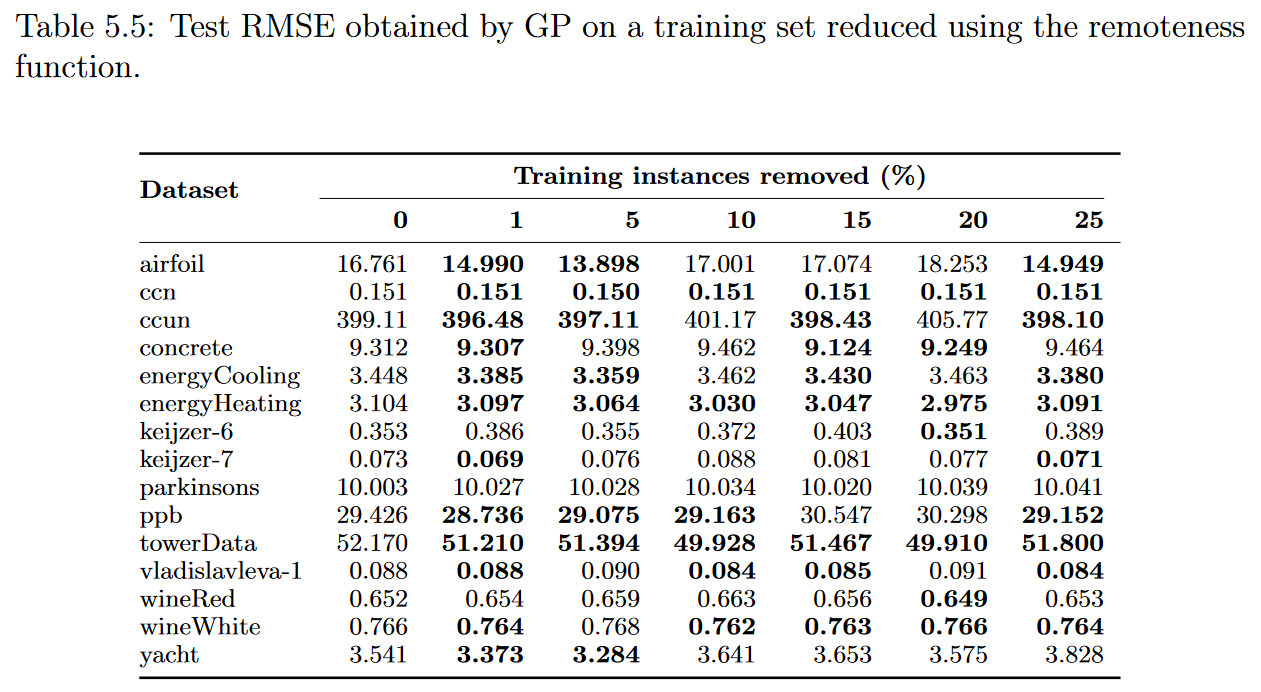
为了防止不必要的广泛性，我们在这一部分中只给出了对于测试集所得到的结果。所有训练集的结果如附录A所示，通过与测试结果的对比，我们观察到基于实例加权的实例选择过程并没有导致任何过拟合的情况(这一结论与分析其他IS方法时得到的结论一致)

为了得到结果的直观概览，我们分析了随着移除实例数量的增加，测试RMSE值的百分比变化。由于重叠线条较多，我们将分析的重点放在数据显示的总体趋势上，只突出特别糟糕或没有定论的结果。图5.8给出了GP运行对应的结果。

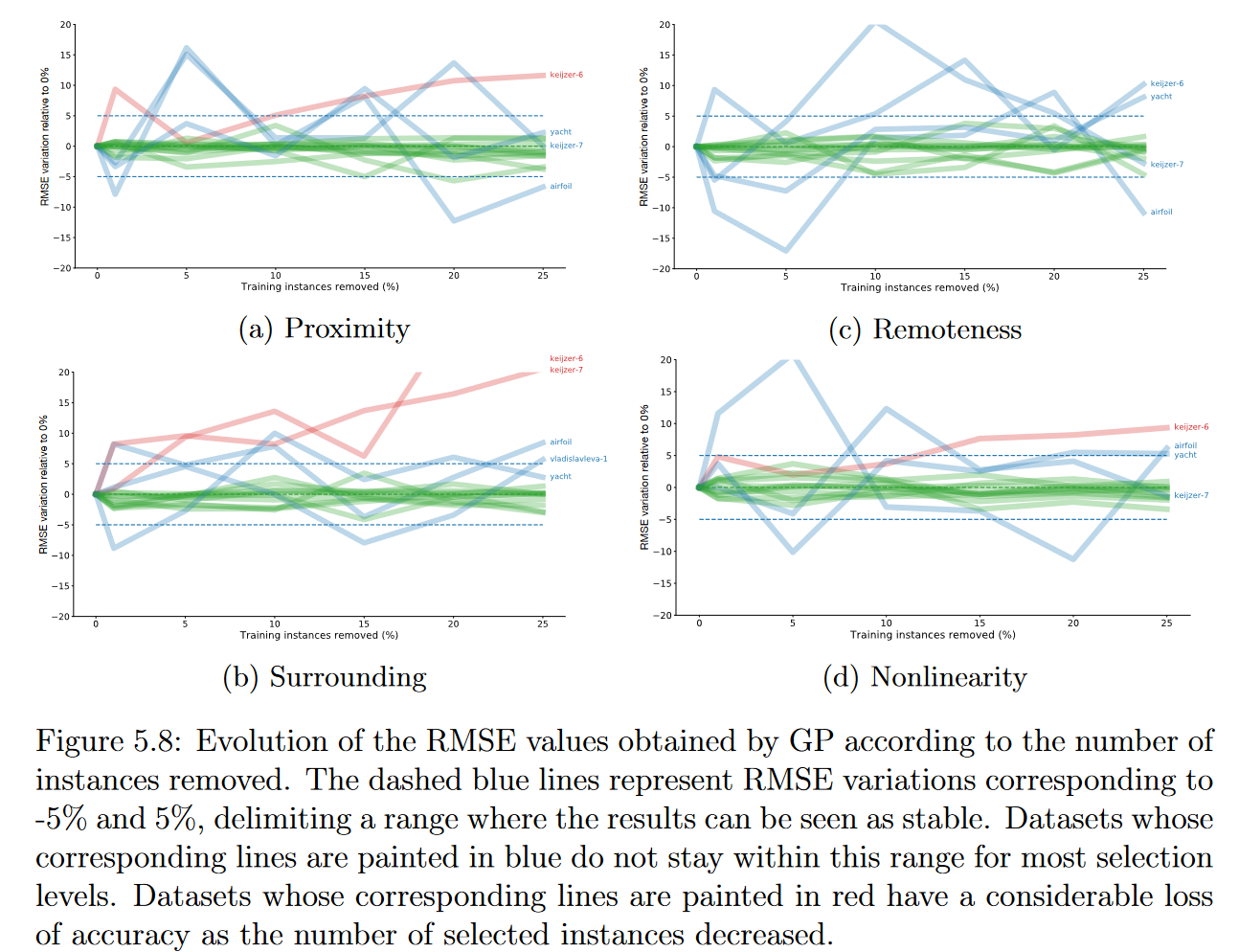
结果表明，对于我们的测试床中的大多数数据集，选择过程对GP执行的回归没有产生强烈的影响，这意味着压缩后的训练集成功地捕获了数据的信息内容。更准确地说，无论使用何种加权函数，对于15个数据集( 14个非线性函数中有9个)中的10个，当使用原始和压缩数据集建立的模型进行比较时，测试的RMSE值没有显著的质量变化，因为对于任何选择水平，相应的RMSE变化都限制在- 5 %至5 %范围内。特别地，对于邻近度和偏远度函数，去除25 %的实例后，在10个数据集中得到的误差值都有所下降。我们观察到对airfoil, keijzer-6, keijzer7, vladislavleva-1, and yacht. 数据集的结果较差或包含结果，其中误差值似乎随着我们选择水平的增加而任意增长或移动。

对于 keijzer-6 and keijzer-7 datasets，这种行为可以解释为，我们使用奇数邻域大小( 5 )，以便为只有一个输入属性的实例分配权重值，其值沿单个均匀分布，在这种情况下，分配给不在输入空间边缘的实例的初始权重肯定是有缺陷的。例如，考虑keijzer-6数据集的一个实例的初始权重计算，如图5.9所示。四个最近邻可以很容易地确定，但是第五个邻居的选择需要在两个与我们想要权衡的实例之间进行任意决策。随着选择的进行，这一问题有减少的趋势，但并没有减轻。然而，如果邻域大小实际上是这些结果背后的唯一原因，那么当我们使用非线性函数时，这两个数据集的行为应该会发生变化，因为对于它们我们使用了k = 2。然而，我们看到结果的随机性水平有所降低，但与其他数据集相比，误差值仍然表明结果较差。

同样有趣的是，结果较差的5个数据集也是输入属性个数( 1 ~ 6)最少的数据集。这可能表明，使用较低的邻域大小- -接近输入属性的数量- -会损害选择过程。如果是这样的话，这种行为应该在GSGP (因为在一个孤立的过程中就会发生破坏)中重复。然而，相反在进行新的实验时，我们将在GSGP结果分析中回到这个问题。

为了验证GP的时间复杂度如何受选择过程的影响，我们分析了该方法为每个数据集创建回归模型所需的中位执行时间。该分析如图5.10所示。尽管结果有一定的不稳定性，但可以看到时间复杂度如预期的那样下降，随着删除实例数量的增加而线性下降。例如，对于keijzer-6和parkinsons数据集，每次执行的时间分别从5秒减少到4秒和从9.7分钟减少到6.6分钟。当然，要充分分析这一方面，就必须考虑到执行选择本身所花费的时间。我们决定不将这些时间包含在分析中，原因有二：( i )在实验过程中，可以看到，与GP诱导其回归模型所花费的时间相比，该任务所花费的时间总是较小的(不到2分钟,即使是最大的数据集)；( ii )我们的实现在创建子集(这样在一次执行中就可以生成尽可能多的子集)之前执行完整的实例排序。因此，用于做出选择的时间不依赖于移除的实例数。为了避免不必要的排序操作，可以对代码进行优化，但这并不能带来任何具体的好处。

图5.10：GP运行的中位执行时间随移除实例数的变化情况。预期的变化对应着时间复杂度的线性下降。

5.3.3.3 Experimental results - GSGP

在这一部分中，我们分析了GSGP结果与准确性和运行时间的关系如何受实例选择过程的影响，重点关注它们与GP获得的结果之间的差异。这种比较的主要目的是研究是否以及在多大程度上，较小的实例数量和由此产生的语义空间的降维能够改善GSGP执行的搜索。实验采用与GP执行中相同的策略进行。表5.7、5.8、5.9和5.10分别给出了使用proximity, surrounding, remoteness, and nonlinearity functions构建的子集训练的GSGP的中位数测试均方根误差。

图5.11遵循与图5.8相同的思路，对结果进行了概述，并展示了随着移除实例数量的增加，误差的变化情况。

上一节的结果表明，使用适当的加权函数，可以压缩训练集，并在使用GP时保持相似的精度。因此，似乎有理由推断，GSGP所产生的回归模型的准确性显著提高的结果可能与其语义空间的维度较小有关。尽管如此，实验表明，尽管语义空间的尺寸较小，GSGP也没有提高其对大多数数据集的预测能力。在去除25%的训练实例后，在15个数据集中的9个数据中，周围函数达到了最好的结果，与原始数据集相比，RMSE变化为负。因此，在这些实验的背景下，没有进一步的证据表明语义空间维度的降低有助于提高GSGP结果。

呈现不确定结果的数据集被缩小到合成数据集：keijzer-6, keijzer-7, and vladislavleva-1.。再次，较小数量的输入属性似乎与这些结果有关，但我们未能证实这一论断。

第二点需要分析的是选择过程对GSGP执行时间的影响。图5.12显示了随着移除实例数量的增加，GSGP执行过程中的时间- -考虑训练和测试阶段- -是如何变化的。与GP的结果相比，执行时间的波动要小得多，并且对于大多数数据集，结果仍然是一致的,与我们的预期一致，呈现线性下降，尽管方式不太明显。合成基再次表现出矛盾的行为，无论删除的实例数多少，执行时间基本上是不变的。

5.3.3.4 Experimental results - Dimensionality reduction methods

在这一部分中，我们分析了应用输入空间降维方法作为选择过程的第一步是否会导致更好的误差值。

我们将Isomap, MDS, PCA, and t-SNE四种方法应用到所有维数≥3的数据集的训练实例中。得到的嵌入用来决定在选择过程中移除哪些实例。然而，所选择的实例具有原始的输入属性数量。所有方法表现相似，由于空间限制，我们将自己限制在GSGP的最佳结果( t-SNE )的方法。

表5.11，5.12，5.13和5.14显示了测试集的中值RMSE，根据50次执行，结果可以更好地可视化在图5.13中。总的来说，结果与前一部分中得到的结果相似。尽管如此，似乎输入降维方法的使用对实例选择过程产生了负面影响。例如，使用非线性函数，GSGP在移除25%的训练实例后，仅在2个数据集中达到了更好的解决方案。

5.3.4 PSE

在这一部分中，我们首先研究了PSE参数的敏感性，然后比较了有无PSE方法的GSGP的性能。PSE参数ρ和λ对选择的实例数量和如何选择有直接影响。为了分析它们对搜索的影响，我们固定了GSGP的参数，并重点研究了当我们改变这些参数时的结果。ρ的取值为分别取5、10和15，改变λ的取值为0.1、0.4和0.7。表5.15给出了这些PSE配置下GSGP得到的训练均方根误差中位数。

采用PSE的实验采用ρ和λ的值，导致中值训练RMSE最小，如表5.15所示。表5.16给出了GSGP和GSGP with PSE (GSGP-PSE)的训练和测试RMSE的中位数。为了确定具有统计学意义的差异，我们在95%的置信水平下进行了Wilcoxon检验，以检验两种方法在50次执行中的RMSE。最后一列的符号N ( H )表示GSGP - PSE比GSGP表现更好(差)的数据集。总体而言，有PSE的GSGP在测试RMSE方面比没有PSE的GSGP表现更好，在5个数据集中表现更好，在1个数据集中表现更差。

图5.14比较了GSGP和GSGP-PSE在两个不同数据集上的训练集和测试集中最优个体的适应度随世代的演化情况。值得注意的是，GSGP的误差总体上高于PSE。例如，从数据集TowerData的收敛性来看，如果我们在1000代停止进化，GSGP的测试误差为25.02，GSG -PSE为23.64。GSGP需要293代才能达到同样的误差。

# Chapter 6 Conclusions and Future Work 在本文中，我们分析了减少GSGP处理的搜索空间大小的方法，并研究了噪声对遗传规划和所提出的实例选择方法的影响。

我们首先分析了在符号回归问题中，与GP相比，噪声数据对GSGP性能的影响。两种方法的性能通过归一化RMSE和从分类文献到回归领域的两种鲁棒性度量，即相对误差增加(RIE)和均衡误差增加(EIE)来衡量，在由15个合成数据集组成的测试床中，每个数据集包含11个不同程度的噪声。

结果表明，当使用RIE度量来分析结果时，GP比GSGP对所有级别的噪声更加鲁棒。然而，当分析NRMSE或EIE值时，GSGP在较低的噪声水平下的鲁棒性优于GP，而在较高的噪声水平下，GP没有显著差异。总体而言，这些结果表明，尽管在低噪声水平下，GSGP的表现优于GP，但在更大的噪声水平下，这些方法的表现相当。

关于降低语义空间维度的策略，我们的工作基于三种主要的策略，包括通过(i)从分类领域调整现有方法来选择实例的方法，(ii)考虑它们的相对重要性，以及(iii)将选择集成到进化过程中的方法。

与第一种策略相关的方法–TCNN和TENN–由分类上下文中使用的著名实例选择方法的修改版本组成，因此它们能够处理回归任务。结果表明，在测试RMSE方面，GSGP在使用整个数据集时表现更好比起当它被使用TCNN或TENN建立的子集馈送时。

第二种策略涉及四个加权函数的应用，以估计每个实例相对于其k个最近邻的重要性。我们还应用了4种降维技术，以改进实例间的紧密度概念。在15个数据集上进行的实验表明，使用加权函数构建的子集能够捕获数据集的底层结构，从而使GSGP能够以相似的质量诱导出更快的模型。另一方面，这些功能的应用并不能证实语义空间大小的减少对GSGP的搜索是有利的。

最后一种策略引入了一种新的方法，称为PSE，它在进化过程中选择实例，同时考虑它们对搜索的影响。实验表明，GSGP与PSE的结合可以提高GSGP的测试RMSE，因此，搜索空间的减小可以对GSGP的搜索产生有利的影响。我们还分析了噪声数据对PSE性能的影响。结果表明，PSE可以像GSGP一样具有鲁棒性，因此，也可以应用在有噪声的现实场景中。

鉴于这些结论，未来可能的工作包括：

研究识别噪声实例的技术，以便在搜索过程中移除它们或最小化它们的重要性；
分析了语义空间维度权重对适应度函数的影响；
研究在实例选择过程中插入噪声实例信息的方法；
分析其他常用回归技术中的实例选择方法，如多项式回归。

References

Miranda L F. Strategies for reducing the size of the search space in semantic genetic programming[J]. 2018.

@article{miranda2018strategies,
  title={Strategies for reducing the size of the search space in semantic genetic programming},
  author={Miranda, Luis Fernando},
  year={2018},
  publisher={Universidade Federal de Minas Gerais}
}