工业控制——张力控制

工控——张力控制

---

提示：写完文章后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

张力控制对在两个加工设备之间作连续运动或静止的被加工材料所受的张力进行自动控制的技术。在各种连续生产线上，各种带材、线材、型材及其再制品，在轧制、拉拔、压花、涂层、印染、清洗以及卷绕等工序中常需要进行张力控制。

---

一、张力是什么？

张力是指在材料受到拉力后发生一定的形变，在其内部产生的一种相互牵引的力。、
在实际工程应用中，为了材料的正常工作，一般需要满足以下要求：

强度要求：在规定载荷作用下的构件不应破坏；
刚度要求：构件应有足够抵抗变形的能力；
稳定性要求：构件应有足够保持原有平衡形态的能力。

其中，变形的基本形式包括拉伸、压缩、剪切、扭转和弯曲等。材料拉伸可以分为4个阶段：即弹性阶段–屈服阶段–强化阶段–局部变形阶段。不是所有的材料都有明显的4个阶段，例如有些脆性材料的屈服阶段、强化阶段会很小。所以，对于未知材料需要通过测试来获取这些参数，从而加深对材料的认识。

在工程实际中，脆性材料在受到一定的力时，变形很小就会断裂；而塑性材料，在断裂前还会出现明显的塑性变形，这些现象都称之为失效。运用CAE进行强度分析，就是判断零件在一定的测试条件下是否会失效。

材料张力计算公式如下：
结合实际运动模型：
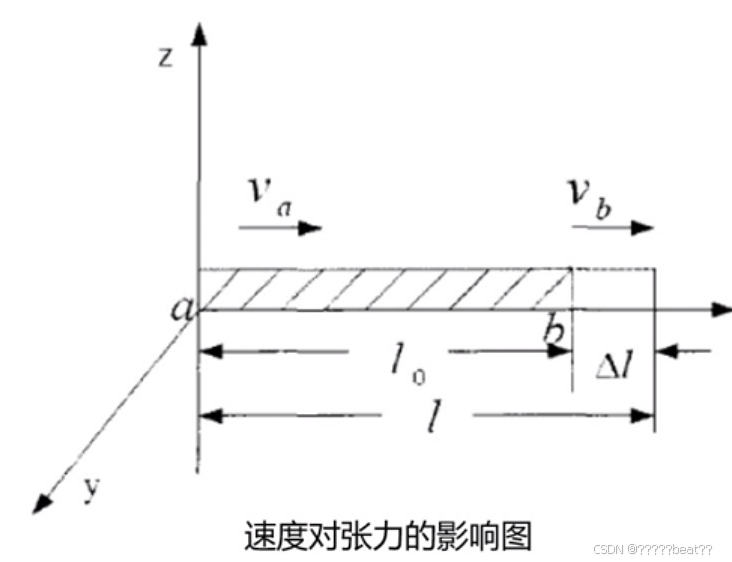张力可表示为：
$$F_n=\frac{AE}{l_0}\int (△v)dt=\frac{AE}{l_0}\int (△v)dt=\frac{AE}{l_0}\int (v_b-v_a)dt$$

张力模型如下：
类比弹簧质量块模型：
$$j\frac{d^{2}x}{dt}=F-kx-f$$
材料固有频率：
$$w_n=\sqrt{\frac{EA}{Jl}}$$
其中E：材料弹性模量、A：材料横截面积、J：电机的惯量、L：材料的长度。

二、张力控制应用场景

在工业生产的诸多行业，经常会遇到卷绕控制问题。如在纸张、纺织品、塑料薄膜、电线、印刷品、磁带、金属带线材等的生产过程中，带料或线材的开卷、卷取张力对产品的质量至关重要，为此要求进行恒张力控制，即在卷绕的过程中使产品承受最佳张力，且自始至终保持不变。若张力过大，会造成加工材料的拉伸变形；张力过小，会使卷取的材料的层与层之间的应力变形，造成收卷不整齐，影响加工质量。在带材卷取系统中，张力控制系统占有重要的位置，而且它相当复杂。

三、张力控制系统及常见张力控制方案

张力控制系统主要包括

• 检测装置：摆杆模拟量、摆杆编码器、张力传感器
• 控制器：PLC、专用控制器、专用变频器
• 执行机构：伺服电机、变频电机、磁粉制动器等。

按控制环路分为开环、闭环

• 开环控制
  没有上图的反馈环节；结构简单、成本低；控制稳定性好、控制精度不高。
• 闭环控制
  如上图所示，闭环调节精度高；需要安装检测机构、成本增加；稳定性不好。

按控制类型：
力矩控制
速度控制
$$F_n=\frac{AE}{l_0}\int (△v)dt=\frac{AE}{l_0}\int (△v)dt=\frac{AE}{l_0}\int (v_b-v_a)dt$$
常见张力控制方式：

四、张力控制卷径计算

在大多数系统中，测量或计算出的卷径直接影响力矩或者速度设定值

---