旋转矩阵的左乘与右乘

前言

  闲来无事把很早之前学习过的旋转矩阵左、右乘的内容回忆并记录一下。如果出现错误的话还请见谅！

---

一、背景

首先明确使用右手系。给出绕X、Y、Z轴旋转的旋转矩阵的定义：
$$R_x(\gamma )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos(\gamma )& -sin(\gamma )\\ 0& sin(\gamma )& cos(\gamma )\end{array}\right]$$
$$R_y(\beta )=\left[\begin{array}{ccc}cos(\beta )& 0& sin(\beta )\\ 0& 1& 0\\ -sin(\beta )& 0& cos(\beta )\end{array}\right]$$
$$R_z(\alpha )=\left[\begin{array}{ccc}cos(\alpha )& -sin(\alpha )& 0\\ sin(\alpha )& cos(\alpha )& 0\\ 0& 0& 1\end{array}\right]$$

明确以下：

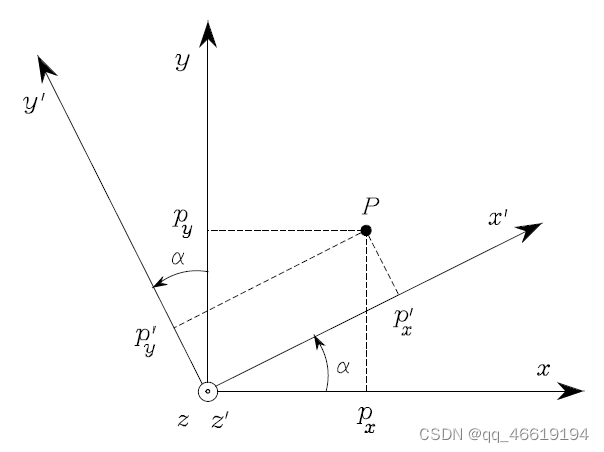
  上图中，坐标系$O-xyz$中$p$点保持不动，坐标系绕z轴旋转 $\alpha$得到新坐标系O-$x\prime y\prime z\prime$，在新坐标系中p的坐标为$p\prime$,则$p$与$p\prime$的关系为：
$$P=R_z(\alpha )P^{\prime }\text{\hspace{1em}(1)}$$
同理对于点旋转的情况，可以这样理解：
  例如在坐标系$O-x\prime y\prime z\prime$中的点$p\prime$绕$z\prime$轴旋转 $\alpha$得到点p，由相对性可知，这个过程可以看作点$p\prime$不动，坐标系$O-x\prime y\prime z\prime$绕$z\prime$轴旋转 $-\alpha$得到新坐标系$O-xyz$，此时$p\prime$在新坐标系$O-xyz$的坐标为$p$，由公式（1）可知，此时$p\prime$与$p$的关系为：
$$P^{\prime }=R_z(-\alpha )P\text{\hspace{1em}(2)}$$
且由于
$$R_z(-\alpha )=R_z^{-1}(\alpha )\text{\hspace{1em}(3)}$$
所以对于公式（2）左右两边同乘$R_z(\alpha )$，得到的点旋转公式同为公式（1）。
  坐标系旋转的公式（1）与点旋转的公式（2）其实物理意义是相同的，都是将空间中的点在新坐标系下的表示转换到旧坐标系下来表示；而坐标系旋转的公式（1）与点旋转的公式（1）物理意义刚好相反，坐标系旋转的公式（1）表示点在新坐标系下的表示转化到旧坐标系下来表示，而点旋转的公式（1）表示为点在旧坐标系下的表示转化到新坐标系下来表示，造成这种情况的原因是点旋转与坐标系旋转的相对性，即点绕某一轴旋转$\alpha$相对来说可以表示为坐标系绕该轴旋转$-\alpha$。在很多实际情况下，坐标系旋转与点旋转利用的都是公式（1），因此需弄清对应的物理意义。
  好了，其实上面不管是坐标系旋转还是点旋转核心都是空间中同一点在不同坐标系下的坐标表示。为了更好的推进以下内容，我们以坐标系旋转来说明旋转矩阵左右乘，并且为了给出一般性的结论，以下内容并不以特定的绕$x、y、z$轴旋转来表示旋转矩阵，而是可以绕任意过原点的轴进行旋转。例如坐标系{0}绕某一过原点的轴旋转得到坐标系{1}，则旋转矩阵表示为$R_0^1$。

二、旋转矩阵的右乘

首先给出结论：绕动坐标系旋转时，旋转矩阵按旋转顺序右乘。
坐标系{0}绕某一在坐标系{0}下过原点的轴旋转得到坐标系{1}，记旋转矩阵为$R_0^1$；
坐标系{1}绕某一在坐标系{1}下过原点的轴旋转得到坐标系{2}，记旋转矩阵为$R_1^2$；
现在坐标系{2}中有一点$p\prime \prime$，该点在坐标系{0}下表示为$p$，则$p\prime \prime$与$p$之间的关系如何表示呢？即$p=R_0^{2}p\prime \prime$中$R_0^2$是什么？
由公式（1）知，坐标系{2}中$p\prime \prime$在坐标系{1}中的表示$p\prime$之间的关系为$p\prime =R_1^{2}p\prime \prime$；同理坐标系{1}中的$p\prime$与坐标系{0}中的$p$之间的关系为$p=R_0^{1}p\prime$，进而$p=R_0^{1}p\prime =R_0^1{R}_1^{2}p\prime \prime$。
所以$R_0^2=R_0^1{R}_1^2$，即绕动坐标系旋转时，旋转矩阵按旋转顺序右乘。

三、旋转矩阵的左乘

首先给出结论：绕定坐标系旋转时，旋转矩阵按旋转顺序左乘。
坐标系{0}绕在坐标系{0}下过原点的$K1$轴旋转$\alpha$得到坐标系{1}，记旋转矩阵为${\bar{R}}_0^1$；
坐标系{1}绕在坐标系{0}下过原点的$K2$轴旋转$\beta$得到坐标系{2}，记旋转矩阵为${\bar{R}}_1^2$;
现在坐标系{2}中有一点$\bar{p}\prime \prime$，该点在坐标系{0}下表示为$\bar{p}$，则$\bar{p}\prime \prime$与$\bar{p}$之间的关系如何表示呢？即$\bar{p}={\bar{R}}_0^2\bar{p}\prime \prime$中${\bar{R}}_0^2$是什么？
思路如下：
  首先坐标系{0}绕在坐标系{0}下过原点的$K1$轴旋转$\alpha$得到坐标系{1}，记旋转矩阵为${\bar{R}}_0^1$，其中${\bar{R}}_0^1$=$R_0^1$。定义两个坐标系{$o\prime$}与{2}，且{$o\prime$}与{0}完全重合、{2}与{1}完全重合。之后将坐标系{$o\prime$}与{2}绕坐标系{0}下过原点的$K2$轴旋转$\beta$,旋转后的坐标系{2}即为上述的坐标系{2}，而坐标系{$o\prime$}为坐标系{0}绕坐标系{0}下过原点的$K2$轴旋转$\beta$得到，四个坐标系关系图如下：

上图中标出了${\bar{R}}_0^1$与${\bar{R}}_1^2$。对于需要求出的${\bar{R}}_0^2$其实与$R_0^2$相同，都是将坐标系{2}下的点转换为坐标系{0}下的点，所以${\bar{R}}_0^2$=$R_0^2$。至此，由上图中四坐标系关系图中的红色转换路线可知，有
$${\bar{R}}_0^2=R_0^2={\bar{R}}_0^1{\bar{R}}_1^2\text{\hspace{1em}(4)}$$
此时发现这并不是旋转矩阵按旋转顺序左乘啊！还是右乘啊！是的，此时还是右乘。那左乘是怎么来的呢？下面说明左乘是怎么来的！！！！！
  首先由坐标系旋转描述可知$R_{o\prime }^2$=${\bar{R}}_0^1$=$R_0^1$，则由上图中四坐标系关系图中的绿转换路线可知，有
$${\bar{R}}_0^2=R_0^2=R_0^{o\prime }{R}_{o\prime }^2=R_0^{o\prime }{R}_0^1\text{\hspace{1em}(5)}$$
没错，这个公式就是旋转矩阵按旋转顺序左乘！！！！
为什么呢？原因是对于旋转矩阵${\bar{R}}_1^2$，由四坐标系关系图发现其有${\bar{R}}_1^2$=${\bar{R}}_1^0{R}_0^{o\prime }{R}_{o\prime }^2=R_1^0{R}_0^{o\prime }{R}_0^1$，然而在实际情况中我们并不能给出像${\bar{R}}_1^2$这样的旋转矩阵，我们只能给出“单纯”的描述旋转的旋转矩阵。举一个具体的例子：
  坐标系{0}绕坐标系{0}的$z$轴旋转$\alpha$得到坐标系{1},而坐标系{1}绕坐标系{0}的$y$轴旋转$\beta$得到坐标系{2}，此时我们只能给出$R_z(\alpha )$与$R_y(\beta )$这样的简单描述旋转的矩阵，并不能得到上述${\bar{R}}_1^2$这样的旋转矩阵，在这个例子中$R_0^1=R_z(\alpha )、R_0^{o\prime }=R_y(\beta )$，所以$R_0^2=R_0^{o\prime }{R}_0^1=R_y(\beta )R_z(\alpha )$，这即为旋转矩阵左乘！即一般都是利用上图中四坐标系关系图中的绿转换路线。

总结

  旋转矩阵左右乘可能在不同领域表现形式不同，但是其核心是一样的。因为旋转矩阵左右乘学习是很早之前完成的，所以本文是按照保留的思路写下来的，可能存在一些错误，希望大家发现错误能及时的反馈给我。

2023/7/29附加

  再解析一下为什么大部分人理解的 “坐标系旋转是右乘，点旋转是左乘”的观点是片面的 。
  其实在文章开头部分就说明了点旋转与坐标系旋转的相对性。由上述背景部分说明了坐标系旋转的矩阵旋转公式$（1）$是将新坐标系下的点转为就旧坐标系下来表示，而点旋转是将旧坐标系下的点转为新坐标系下来表示。为更好的理解，用下面一个点旋转例子来进一步说明：
  eg:坐标系$O-xyz$中的一点$p$先绕$z$轴旋转$\alpha$，再绕$y$轴旋转$\beta$，得到点$p\prime$。
  现在利用点旋转与坐标系旋转的相对性来推到点旋转的旋转矩阵。首先我们得知道点旋转相对的坐标系旋转是绕动坐标轴旋转的，所以有$p=R_z(-\alpha )R_y(-\beta )p\prime$，但是点旋转是将旧坐标系下的点转为新坐标系下来表示，所以由上面的公式可推导出$p\prime =R_y(\beta )R_z(\alpha )p$，此时旋转矩阵$R=R_y(\beta )R_z(\alpha )$，这也就是所谓的“点旋转是左乘”！其实其本质还是在解释旋转矩阵右乘，只不过没有弄明白坐标系旋转和点旋转的相对性以及最终结果是在新坐标系还是旧坐标系下来表示，所以误将其认为是在解释旋转矩阵左乘。