【LGR-197-Div.2】洛谷 10 月月赛 I &「SFMOI」Round I 比赛 A ~ C 题解

【LGR-197-Div.2】洛谷 10 月月赛 I &「SFMOI」Round I

打舒服了。

A.Strange Cake Game

题面：

题目背景

English statement. You must submit your code at the Chinese version of >the statement.

小 $\mathcal{W}$ 和 小 $\mathcal{M}$ 在 CF 庄园里分蛋糕。

题目描述

有一块面积为 $n\times m$ 的矩形蛋糕。记其左上角顶点为 $(0,0)$，右下角顶点为 $(n,m)$，右上角顶点为 $(0,m)$。

蛋糕上分布着 $k$ 块巧克力，第 $i$ 块的位置为 $(x_i-0.5,y_i-0.5)$。一个点上可能有不止一块巧克力。

小 M 和 小 W 要切蛋糕。蛋糕刀起初在 $(0,0)$，小 W 先手，轮流移动蛋糕刀。设蛋糕刀在 $(x,y)$，则它可以被移动到 $(x,y+1)$ 或 $(x+1,y)$。

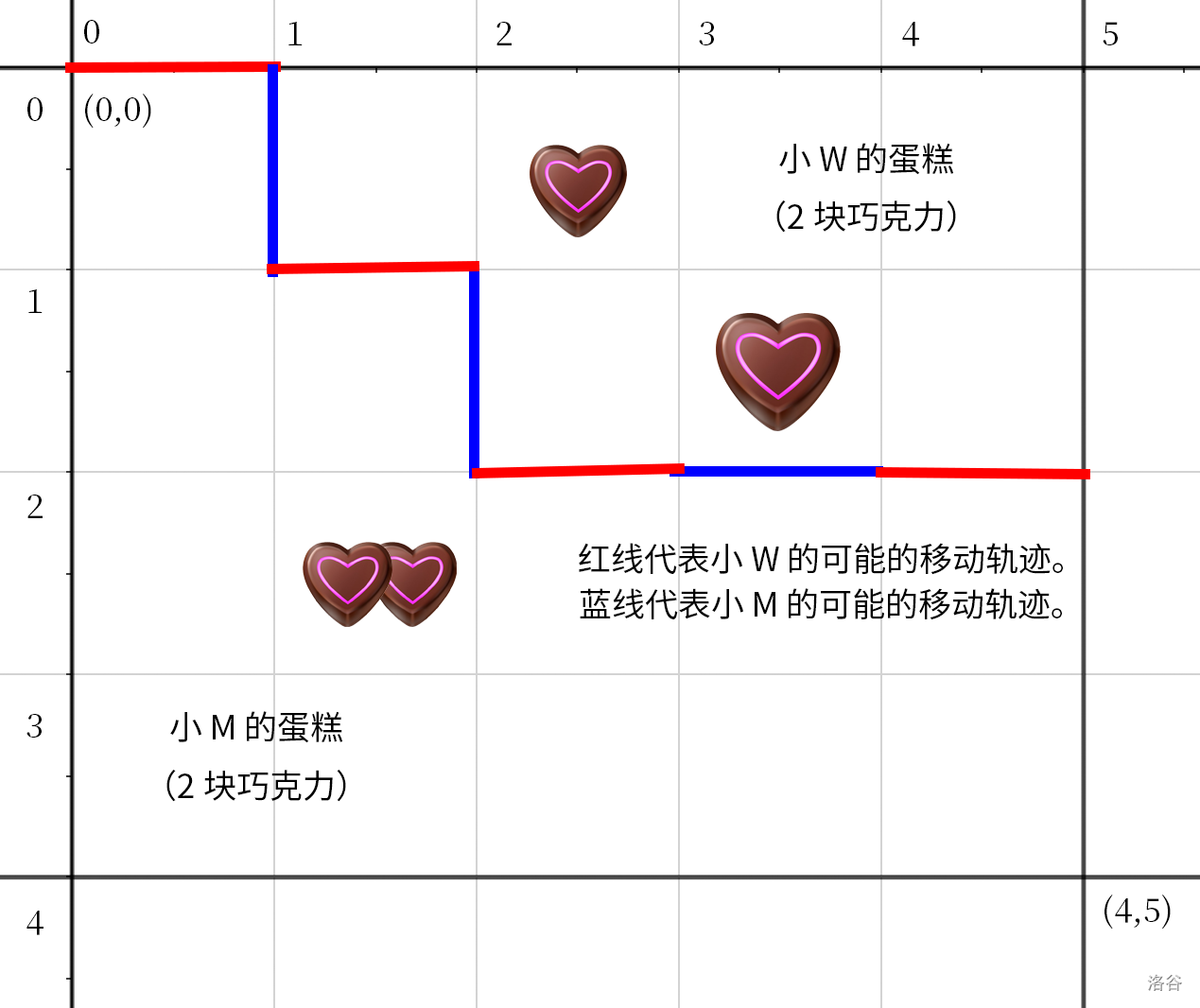
在若干步后，蛋糕会被切割轨迹完全分成两个部分——右上角的部分归小 W，左下角的部分归小 M。小 W 和小 M 都想吃到最多的巧克力，请帮他们计算：如果双方都按照最优策略行动，小 W 能分到几块巧克力。

如下是蛋糕的示例和一种可能的切蛋糕的方式。

输入格式

第一行，两个正整数 $n,m$，含义见题面。

第二行，一个整数 $k$ ，表示巧克力块数。

接下来 $k$ 行，每行两个正整数 $x_i,y_i$，表示第 $i$ 块巧克力的坐标为 $(x_i-0.5,y_i-0.5)$。

注意：第 $i$ 块巧克力的坐标为 $(x_i-0.5,y_i-0.5)$。一个格子上可能有多块巧克力。

输出格式

输出一个整数，代表小 W 最多能拿到的巧克力块数。

样例 #1

样例输入 #1

3 3
1
1 3

样例输出 #1

1

提示

数据范围

本题采用捆绑测试。

• Subtask 1（5 pts）：$n=m=1$；
• Subtask 2（10 pts）：$1\le n\times m\le 60$；
• Subtask 3（15 pts）：$1\le n\times m\le 10^5$；
• Subtask 4（20 pts）：$k=1$；
• Subtask 5（50 pts）：无特殊限制。

对于 $100\%$ 的数据，保证：

• $0\le k\le 2\times 10^5$；
• $1\le n,m\le 10^{18}$；
• $1\le x_i\le n$，$1\le y_i\le m$。

简单博弈，划分的面积肯定是越大越好，

所以从原点走一条折线到终点肯定最优，判断是否蛋糕在折线上方。

AC-code：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 2e5+5;
int n,m,k;
signed main() {
    n = rd(),m = rd();
    k = rd();
    int ans = 0;
    for(int i = 1;i<=k;i++) {
        int x = rd(),y = rd();
        if(x > y) ans++; 
    }
    wt(k - ans);
	return 0;
}

B1.Strange Madoka Game

题面：

题目背景

English statement. You must submit your code at the Chinese version of the statement.

いつも君の側にいるから / 无论何时我都与你同在
儚すぎて / 世界如此虚幻
消えて行きそうな世界 / 似乎随时随地都会消失
だけど君がいる / 然而只要有你
それだけで守りたいと思った / 我就心甘情愿将它守护

题目描述

本题和 B2 是不同的问题，请分别仔细阅读两题题面。

这是一道交互题。

提示：我们在题目描述的最后提供了一份简要的、形式化描述的题面。

圆和焰在玩游戏。

圆在心中想了一个非负整数 $m$，让焰猜出 $m$ 的值。当然，圆不会为难焰，所以 $0\le m\le 10^{17}$。圆不会作弊，也就是说，圆不会悄悄更换想好的数字。

焰可以问圆：对于正整数 $x$，$m\mathrm{mod}x$ 的值是多少。焰需要用最少的询问次数来猜出 $m$ 的值。（为了得到全部分数，最多只能使用 $2$ 次询问。）

圆一共和焰玩了 $T$ 次游戏。然而，焰的数学很差，于是她找来了你，来帮她猜出这 $T$ 次游戏的答案。

形式化地：有一个隐藏的非负整数 $m\in [0,10^{17}]$。每次询问给定正整数 $x$，回答 $m\mathrm{mod}x$。用最少的询问次数找出 $m$。共有 $T$ 组测试数据。$m$ 的数值在事先确定，不会根据询问变化，也就是说，交互库是非适应性的。

【实现细节】

对于每个测试点，输入一行一个正整数 $T$，表示游戏次数。

对于每组测试数据，你可以用以下的格式发起一次询问：

• $\text{? }x$：询问 $m\mathrm{mod}x$ 的值。你需要保证 $x$ 是正整数，且 $x\in [1,4\times 10^8]$。

  从标准输入流读入一个整数表示答案。特别地，若整数是 $\text{-1}$，你的程序已经被判定为 $\text{Wrong Answer}$，此时你需要立刻终止程序。

你可以用以下的格式回答答案：

• $\text{! }m$：回答 $m$ 的值。

在发起询问后，需要刷新缓冲区，否则可能导致 TLE。

• 在 C++ 中，使用 fflush(stdout) 或 cout.flush()。 特别地，利用 std::endl 来换行也会刷新缓冲区。
• 在 Pascal 中，使用 flush(output)。
• 在 Python 中，使用 stdout.flush()。
• 对于其它语言，可自行查阅文档。

输入格式

见【实现细节】。

输出格式

见【实现细节】。

样例 #1

样例输入 #1

1

1

2

样例输出 #1

? 2

? 3

! 5

提示

数据范围

对于 $100\%$ 的数据，保证 $1\le T\le 100$，$m$ 为非负整数，$0\le m\le 10^{17}$。

评分方式

记单个测试点中，你的询问次数的最大值为 $Q$。则得分 $\mathrm{score}$ 如下所示：

$$\begin{array}{r}\mathrm{score}=\{\begin{array}{ll}0,& Q\in [81,+\infty )\\ 10,& Q\in [11,81)\\ 25,& Q\in [3,11)\\ 50,& Q\in [0,3)\end{array}\end{array}$$

本题得分为所有测试点得分的最小值。

B1 交互题

考虑用两个相差为一的数 $x,y$ 去询问，

因为 $m=ax+by$ 必定成立，那么 $ax\equiv m(\mathrm{mod}y)$、$by\equiv m(\mathrm{mod}x)$ 也成立。

把 $m$ 看做未知数，套上 $\mathrm{CRT}$ 就可以求解了。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define LL long long
int query(int x) {
    cout<<"? "<<x<<endl;
    int c;
    cin>>c;
    return c;
}

void answer(int x) {
    cout<<"! "<<x<<endl;
}

void exgcd(int a,int b,int &x,int &y) {
	if(!b) {
		x = 1;
		y = 0;
	}else  {
		exgcd(b,a%b,x,y);
		int t = x;
		x = y;
		y = t - a/b * y;
	}
}

LL CRT(int k, LL* a, LL* r) {
  LL n = 1, ans = 0;
  for (int i = 1; i <= k; i++) n = n * r[i];
  for (int i = 1; i <= k; i++) {
    LL m = n / r[i], b, y;
    exgcd(m, r[i], b, y);  
    ans = (ans + a[i] * m * b % n) % n;
  }
  return (ans % n + n) % n;
}


void solve() {
    int x = query(399999999),y = query(400000000);
    int a[3] = {0,x,y},r[3] = {0,399999999,400000000};
    if(x == y) {answer(x);return;}
    else {
        int k = CRT(2,a,r);
        answer(k);
        return;
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int T;
    cin>>T;
    while(T--) solve();
	return 0;
}

B2.Strange Homura Game

题面：

题目背景

English statement. You must submit your code at the Chinese version of >the statement.

伝えたいコトバは たったひとつ / 想要传达的言语 唯有一个
キミがいたから 強くなれた / 因有你在 我变坚强了
2 人ならどんな空も飛べるね / 只要两人一起就能任意飞翔
キミをいつでも 信じてるから / 因为一直都 坚信着你
ずっとずっと夢を見ていよう / 能同做此梦不复醒吧

题目描述

本题和 B1 是不同的问题，请分别仔细阅读两题题面。

这是一道交互题。

提示：我们在题目描述的最后提供了一份简要的、形式化描述的题面。

焰和圆在玩游戏。

焰在心中想了一个正整数 $m$，让圆猜出 $m$ 的值。当然，焰不会为难圆，所以 $2\le m\le 10^{17}$。焰不会作弊，也就是说，焰不会悄悄更换想好的数字。

圆可以问焰：对于非负整数 $x$，$x\mathrm{mod}m$ 的值是多少。圆需要用最少的询问次数来猜出 $m$ 的值。（为了得到全部分数，最多只能使用 $2$ 次询问。）

焰一共和圆玩了 $T$ 次游戏。圆的数学很好，在 $\varepsilon $ 秒内就秒了这题，但是她在军训，于是她找来了你，来帮她猜出这 $T$ 次游戏的答案。

形式化地：有一个隐藏的正整数 $m\in [2,10^{17}]$。每次询问给定非负整数 $x$，回答 $x\mathrm{mod}m$。用最少的询问次数找出 $m$。共有 $T$ 组测试数据。$m$ 的数值在事先确定，不会根据询问变化，也就是说，交互库是非适应性的。

【实现细节】

对于每个测试点，输入一行一个正整数 $T$，表示游戏次数。

对于每组测试数据，你可以用以下的格式发起一次询问：

• $\text{? }x$：询问 $x\mathrm{mod}m$ 的值。你需要保证 $x$ 是非负整数，且 $x\in [0,10^{18}]$。

  从标准输入流读入一个整数表示答案。特别地，若整数是 $\text{-1}$，你的程序已经被判定为 $\text{Wrong Answer}$，此时你需要立刻终止程序。

你可以用以下的格式回答答案：

• $\text{! }m$：回答 $m$ 的值。

在发起询问后，需要刷新缓冲区，否则可能导致 TLE。

• 在 C++ 中，使用 fflush(stdout) 或 cout.flush()。 特别地，利用 std::endl 来换行也会刷新缓冲区。
• 在 Pascal 中，使用 flush(output)。
• 在 Python 中，使用 stdout.flush()。
• 对于其它语言，可自行查阅文档。

输入格式

见【实现细节】。

输出格式

见【实现细节】。

样例 #1

样例输入 #1

1

0

1

样例输出 #1

? 5

? 1

! 5

提示

数据范围

对于 $100\%$ 的数据，保证 $1\le T\le 100$，$m$ 为正整数，$2\le m\le 10^{17}$。

评分方式

记单个测试点中，你的询问次数的最大值为 $Q$。则得分 $\mathrm{score}$ 如下所示：

$$\begin{array}{r}\mathrm{score}=\{\begin{array}{ll}0,& Q\in [101,+\infty )\\ 30,& Q\in [3,101)\\ 50,& Q\in [0,3)\end{array}\end{array}$$

本题得分为所有测试点得分的最小值。

我们先考虑询问一个数后的信息：

我们假设询问一个数 $x$，我们可以得到 $x\equiv d(\mathrm{mod}m)$。

也就是 $x=d+km$，那么简单变形 $x-d=km$

那么询问 $x-d$ （$x>d$） 肯定是 $0$ （$x-d\equiv 0(\mathrm{mod}m)$）。

我们怎么通过这个信息解出 $m$ 呢？

发动人类智慧：$x-d-1\equiv m-1(\mathrm{mod}m)$。

我们只需要询问 $x-d-1$ 即可得到 $m-1$。

最后将询问的值加一作为答案回答！

因为 $x\in [0,10^{18}]$ 而 $m\in [0,10^{17}]$，所以当我们询问 $10^{18}$ 时必定有 $x>d$。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long

int query(int x) {
    cout<<"? "<<x<<endl;
    int c;
    cin>>c;
    return c;
}

void answer(int x) {
    cout<<"! "<<x<<endl;
}

void solve() {
    const int N = 1e18;
    int x = query(N);
    int k = N - x;
    int y = query(k - 1);
    answer(y + 1);
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);cout.tie(nullptr);
    int T;cin>>T;
    while(T--) solve();
	return 0;
}

C.Strange Train Game

题面：

题目背景

English statement. You must submit your code at the Chinese version of the statement.

SFM 团队又断网了，于是玩起了 Mini Metro，结果发现游戏更新了，列车要自己组装，于是有了这题。

题目描述

提示：我们在题目描述的最后提供了一份简要的、形式化描述的题面。

SFM 号列车由 $n$ 节车厢组成，编号为 $1\sim n$。每节车厢有一个舒适度 a i ∈ { 0 , 1 } a_i\in \{0,1\} ai​∈{0,1}，$0$ 代表不舒适，$1$ 代表舒适。管理组想要让舒适的车厢的编号尽小，也就是说，让 $a$ 的字典序最大。

为此，管理组运来了一辆 $n$ 节车厢的备用车，舒适度表示为 b i ∈ { 0 , 1 } b_i\in \{0,1\} bi​∈{0,1}。共有 $m$ 个可进行的操作，第 $i$ 个操作的操作参数为 $l_i,r_i$，表示 $\forall l_i\le k\le r_i$，交换 $a_k,b_k$。

可以从小到大依次决定是否执行每个操作，但是一共有 $2^m$ 种方案，于是，管理组找来了你，帮忙选出一种最优的方案，最大化 $a$ 的字典序。只需要输出最终得到的 $a$ 即可。

形式化地：给定长度为 $n$ 的 $01$ 串 $a,b$，给定 $2m$ 个正整数 $l_i,r_i$。对于 $i=1,2,\cdots ,m$，依次执行以下操作：

• 选择是否执行第 $i$ 次操作。
  • 如果执行，则对于 $k=l_i,l_i+1,\cdots ,r_i$，交换 $a_k,b_k$。

最大化 $a$ 的字典序并输出最终的结果。

输入格式

第一行，两个正整数 $n,m$，表示字符串的长度和操作次数。

第二行，一个长度为 $n$ 的 $01$ 串 $a$。

第三行，一个长度为 $n$ 的 $01$ 串 $b$。

接下来 $m$ 行，每行两个正整数 $l_i,r_i$，描述第 $i$ 个操作。

输出格式

输出一行长度为 $n$ 的 $01$ 串，表示最优操作后的 $a$。

样例 #1

样例输入 #1

10 5
0101011001
0101001110
5 10
2 6
1 10
6 6
3 4

样例输出 #1

0101011110

提示

本题采用捆绑测试。

• Subtask 1（20 pts）：$1\le n,m\le 20$；
• Subtask 2（30 pts）：$l_i$ 互不相同，$a_i\ne b_i$；
• Subtask 3（30 pts）：$1\le n,m\le 10^3$；
• Subtask 4（20 pts）：无限制；

对于 $100\%$ 的数据，保证：

• $1\le n,m\le 2\times 10^5$；
• $1\le l_i\le r_i\le n$。

我是蒟蒻，只想到了 $\mathcal{O}(n\log n)$ 的做法。

SubTask 1

考虑暴力，枚举每一种选择情况，时间复杂度 $\mathcal{O}(2^{m}n\log n)$ 。

code:

namespace baoli{
array<int,2> w[N];
string A,B;
void start() {
    auto cmp = [&](string x,string y) -> bool{
        for(int i = 0;i<x.size();i++) {
            if(x[i] < y[i]) 
                return true;
            else if(x[i] > y[i]) 
                return false;
        }
        return false;
    };
    for(int i = 0;i<m;i++) cin>>w[i][0]>>w[i][1];
    for(int i = 0;i<n;i++) A.push_back('0');
    for(int k = 0;k<(1<<m);k++) {
    	sgt::build(1,1,n);
        B.clear();
        for(int i = 0;i<m;i++) 
            if((k >> i) & 1)
				sgt::update(1,1,n,w[i][0],w[i][1],1); // <- 区间加单点查线段树的更新操作
        for(int i = 0;i<n;i++) {
            int re = sgt::query(1,1,n,i + 1) & 1; // <- 区间加单点查线段树的查询操作 （判断目前位是否被交换）
            if(re) B.push_back(b[i]);
            else B.push_back(a[i]);
        }
        if(cmp(A,B)) A = B;// 比较答案
    }
    cout<<A;
}
}

SubTask 2

当每一位 $a,b$ 字符都不同，且 $l_i$ 互不相同，我们贪心的使用区间交换。

从第 $1$ 位到最后 $1$ 位遍历，$a$ 中每有一位非 $1$ ，考虑是否有从当前点出发的区间交换操作并使用。

code:

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int s[N<<2],tag[N<<2];
void build(int p,int pl,int pr) {
    tag[p] = 0;
    s[p] = 0;
    if(pl == pr) {s[p] = 0;return;}
    build(ls,pl,mid);
    build(rs,mid+1,pr);
}
void addtag(int p,int pl,int pr,int d) {
    tag[p] += d;
    s[p] += (pr - pl + 1) * d;
} 
void push_down(int p,int pl,int pr) {
    if(tag[p]) {
        addtag(ls,pl,mid,tag[p]);
        addtag(rs,mid+1,pr,tag[p]);
        tag[p] = 0;
    }
}
void update(int p,int pl,int pr,int l,int r,int d) {
    if(l <= pl && pr <= r) {addtag(p,pl,pr,d);return;}
    push_down(p,pl,pr);
    if(l <= mid) update(ls,pl,mid,l,r,d);
    if(r > mid) update(rs,mid+1,pr,l,r,d);
}

int query(int p,int pl,int pr,int k) {
    if(pl == pr) return tag[p];
    push_down(p,pl,pr);
    if(k <= mid) return query(ls,pl,mid,k);
    else return query(rs,mid+1,pr,k);
}
}
signed main() {
    cin>>n>>m;
    cin>>a;
    cin>>b;
    for(int i = 1;i<=m;i++) {
        int x,y;
        cin>>x>>y;
        x--,y--;
        t[x].emplace_back(y);
    }
    
    for(int i = 0;i<n;i++) {
        int x = a[i] - '0',y = b[i] - '0';
        if(((sgt::query(1,1,n,i) & 1) ? y : x) == 1) {putchar('1');continue;}
        else {
            for(int v : t[i])
                sgt::update(1,1,n,i,v,1);
            
            putchar(((sgt::query(1,1,n,i) & 1) ? y : x) + '0');
        }
    }


	return 0;
}

Subtask 3

神秘做法，不清楚。

$\mathcal{O}(n\log n)$ 正解

考虑 SubTask 2 给我们带来的启示：

1. 只有 $a_i\ne b_i$ 时，才考虑交换操作。
2. 化归为 SubTask 2 的 $l_i$ 互不相等的情况，就可以求得正解。

针对第一条启示，我们可以挑出 $a_i\ne b_i$ 的位置 $s{t}_i$（加入栈中），同时将交换区间的 $l_i,r_i$ 改为 $st$ 中的一段连续区间，只在上面计算答案。

针对第二条启示，我们来看下面这张图：

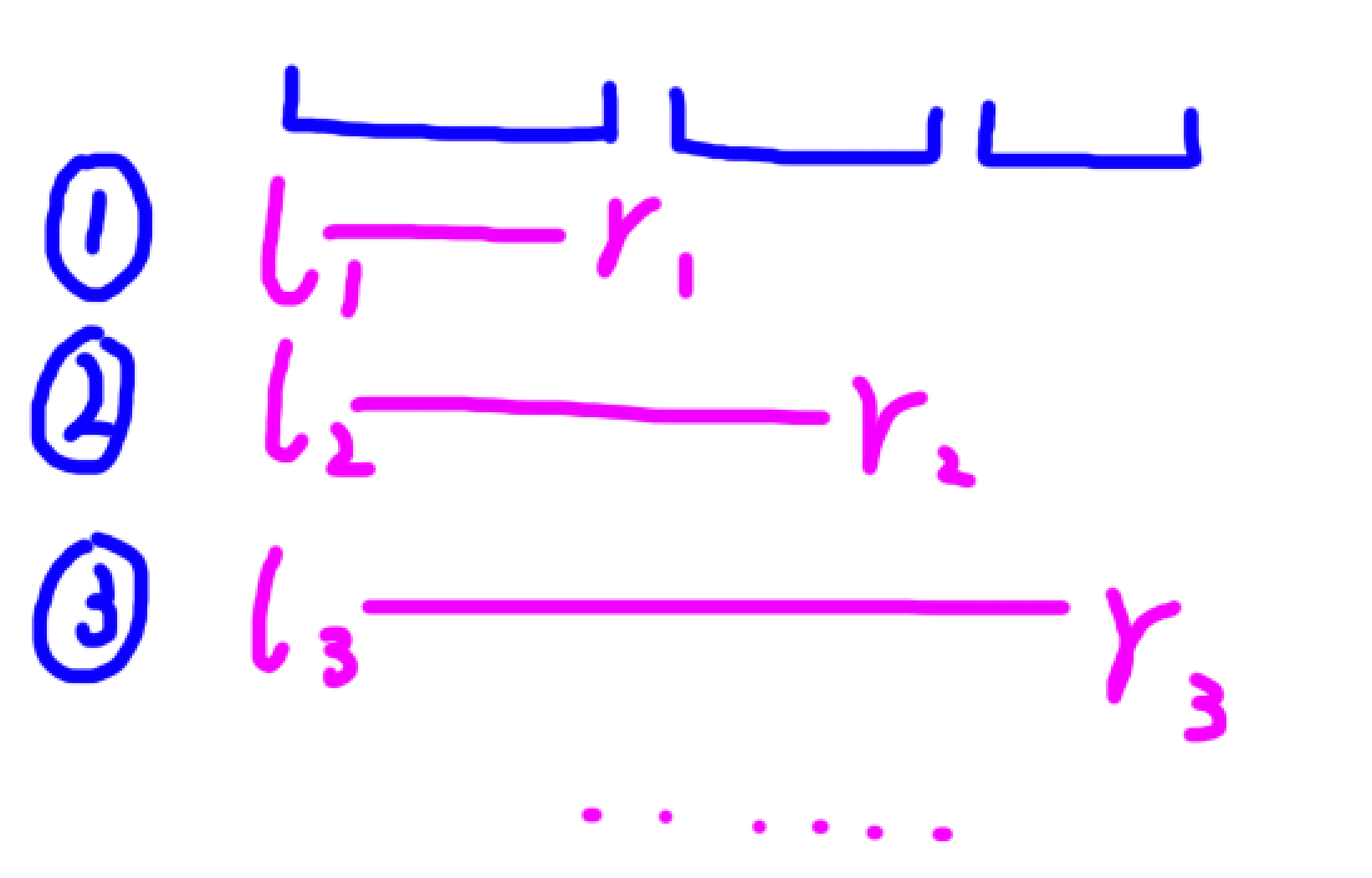
类似于异或线性基，我们可以将 任意选择这 $n$ 个同起点的区间交换操作 转变为 任意选择 $n$ 个互不相交的区间交换操作。

大家可以自行模拟一下。

那么，我们只需要将每个同起点的区间排序，去重（因为我们在做第一条启示时，可能会出现相同区间的情况），然后将大区间拆分成小区间，即可化归为 SubTask 2，AC 此题。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2e5+5;
int n,m,st[N],top;
char c[N],d[N];
vector<int> t[N];

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int s[N<<2],tag[N<<2];
void addtag(int p,int pl,int pr,int d) {
    tag[p] += d;
    s[p] += (pr - pl + 1) * d;
} 
void push_down(int p,int pl,int pr) {
    if(tag[p]) {
        addtag(ls,pl,mid,tag[p]);
        addtag(rs,mid+1,pr,tag[p]);
        tag[p] = 0;
    }
}
void update(int p,int pl,int pr,int l,int r,int d) {
    if(l <= pl && pr <= r) {addtag(p,pl,pr,d);return;}
    push_down(p,pl,pr);
    if(l <= mid) update(ls,pl,mid,l,r,d);
    if(r > mid) update(rs,mid+1,pr,l,r,d);
}

int query(int p,int pl,int pr,int k) {
    if(pl == pr) return tag[p];
    push_down(p,pl,pr);
    if(k <= mid) return query(ls,pl,mid,k);
    else return query(rs,mid+1,pr,k);
}
}

int ans[N];

signed main() {
    scanf("%lld %lld",&n,&m);
    scanf("%s %s",c + 1,d + 1);
    for(int i = 1;i<=n;i++) {
        if(c[i] != d[i])
            st[++top] = i;
        else ans[i] = c[i] - '0';
    }
    st[++top] = n + 1;
    for(int i = 1;i<=m;i++) {
        int x,y;
        scanf("%lld%lld",&x,&y);
        x = lower_bound(st + 1,st + top + 1,x) - st;
        y = upper_bound(st + 1,st + top + 1,y) - st - 1;
        if(x > y) continue;
        t[x].emplace_back(y);
    }
    for(int i = 1;i<top;i++) {
        int x = c[st[i]] - '0',y = d[st[i]] - '0';
        int r = i;
        sort(t[i].begin(),t[i].end());
        int tc = unique(t[i].begin(),t[i].end()) - t[i].begin() - 1;
        for(int v = 0;v<=tc;v++) {
                if(r^i) t[r].emplace_back(t[i][v]);
                else if((sgt::query(1,1,top,i) & 1 ? y : x) != 1) 
				    sgt::update(1,1,top,i,t[i][v],1);
                r = t[i][v] + 1;
        }
        ans[st[i]] = (sgt::query(1,1,top,i) & 1) ? y : x;
    }
    for(int i = 1;i<=n;i++) printf("%lld",ans[i]);
	return 0;
}

复杂度分析：

这里的拆区间操作最坏时间复杂度是 $O(m\log m)$。

最坏情况：

考虑对于每一位 $i$ ，都有 $[i\sim (i+1+n)/2]$ 和 $[i\sim i]$ 两个区间交换操作。

在 第 $1$ 位 额外有一个 $[1\sim n]$ 的区间交换操作，

这个 $[1\sim n]$ 区间交换操作会从大区间一路折半直到区间大小为 1 的时候才停止。

而这种区间只能存在一个，故时间复杂度最坏为 $O(m\log m)$。

线段树查询复杂度为 $O(n\log n)$

故复杂度大概是 $O(n\log n+m\log m)$ (因为拆区间的复杂度是独立的)

我赛时写代码比较唐，可以用异或前缀和取代线段树降为 $O(n+m\log m)$

因为 $n,m$ 同阶，所以复杂度 $O(m\log m)$不变