P8820 [CSP-S 2022] 数据传输
可怜的cnblog被(昨天DDos + 今天CC)攻击了(望周知!),只好先发在 CSDN
题面:
题目描述
小 C 正在设计计算机网络中的路由系统。
测试用的网络总共有 n n n 台主机,依次编号为 1 ∼ n 1 \sim n 1∼n。这 n n n 台主机之间由 n − 1 n - 1 n−1 根网线连接,第 i i i 条网线连接个主机 a i a_i ai 和 b i b_i bi。保证任意两台主机可以通过有限根网线直接或者间接地相连。受制于信息发送的功率,主机 a a a 能够直接将信息传输给主机 b b b 当且仅当两个主机在可以通过不超过 k k k 根网线直接或者间接的相连。
在计算机网络中,数据的传输往往需要通过若干次转发。假定小 C 需要将数据从主机 a a a 传输到主机 b b b( a ≠ b a \neq b a=b),则其会选择出若干台用于传输的主机 c 1 = a , c 2 , … , c m − 1 , c m = b c_1 = a, c_2, \ldots, c_{m - 1}, c_m = b c1=a,c2,…,cm−1,cm=b,并按照如下规则转发:对于所有的 1 ≤ i < m 1 \le i < m 1≤i<m,主机 c i c_i ci 将信息直接发送给 c i + 1 c_{i + 1} ci+1。
每台主机处理信息都需要一定的时间,第 i i i 台主机处理信息需要 v i v_i vi 单位的时间。数据在网络中的传输非常迅速,因此传输的时间可以忽略不计。据此,上述传输过程花费的时间为 ∑ i = 1 m v c i \sum_{i = 1}^{m} v_{c_i} ∑i=1mvci。
现在总共有 q q q 次数据发送请求,第 i i i 次请求会从主机 s i s_i si 发送数据到主机 t i t_i ti。小 C 想要知道,对于每一次请求至少需要花费多少单位时间才能完成传输。
输入格式
输入的第一行包含三个正整数 n , Q , k n, Q, k n,Q,k,分别表示网络主机个数,请求个数,传输参数。数据保证 1 ≤ n ≤ 2 × 10 5 1 \le n \le 2 \times {10}^5 1≤n≤2×105, 1 ≤ Q ≤ 2 × 10 5 1 \le Q \le 2 \times {10}^5 1≤Q≤2×105, 1 ≤ k ≤ 3 1 \le k \le 3 1≤k≤3。
输入的第二行包含 n n n 个正整数,第 i i i 个正整数表示 v i v_i vi,保证 1 ≤ v i ≤ 10 9 1 \le v_i \le {10}^9 1≤vi≤109。
接下来 n − 1 n - 1 n−1 行,第 i i i 行包含两个正整数 a i , b i a_i, b_i ai,bi,表示一条连接主机 a i , b i a_i, b_i ai,bi 的网线。保证 1 ≤ a i , b i ≤ n 1 \le a_i, b_i \le n 1≤ai,bi≤n。
接下来 Q Q Q 行,第 i i i 行包含两个正整数 s i , t i s_i, t_i si,ti,表示一次从主机 s i s_i si 发送数据到主机 t i t_i ti 的请求。保证 1 ≤ s i , t i ≤ n 1 \le s_i, t_i \le n 1≤si,ti≤n, s i ≠ t i s_i \ne t_i si=ti。
输出格式
Q Q Q 行,每行一个正整数,表示第 i i i 次请求在传输的时候至少需要花费多少单位的时间。
样例 #1
样例输入 #1
7 3 3 1 2 3 4 5 6 7 1 2 1 3 2 4 2 5 3 6 3 7 4 7 5 6 1 2样例输出 #1
12 12 3提示
【样例解释 #1】
对于第一组请求,由于主机 4 , 7 4, 7 4,7 之间需要至少 4 4 4 根网线才能连接,因此数据无法在两台主机之间直接传输,其至少需要一次转发;我们让其在主机 1 1 1 进行一次转发,不难发现主机 1 1 1 和主机 4 , 7 4, 7 4,7 之间都只需要两根网线即可连接,且主机 1 1 1 的数据处理时间仅为 1 1 1,为所有主机中最小,因此最少传输的时间为 4 + 1 + 7 = 12 4 + 1 + 7 = 12 4+1+7=12。
对于第三组请求,由于主机 1 , 2 1, 2 1,2 之间只需要 1 1 1 根网线就能连接,因此数据直接传输就是最优解,最少传输的时间为 1 + 2 = 3 1 + 2 = 3 1+2=3。
【样例 #2】
见附件中的
transmit/transmit2.in与transmit/transmit2.ans。该样例满足测试点 2 2 2 的限制。
【样例 #3】
见附件中的
transmit/transmit3.in与transmit/transmit3.ans。该样例满足测试点 3 3 3 的限制。
【样例 #4】
见附件中的
transmit/transmit4.in与transmit/transmit4.ans。该样例满足测试点 20 20 20 的限制。
【数据范围】
对于所有的测试数据,满足 1 ≤ n ≤ 2 × 10 5 1 \le n \le 2 \times {10}^5 1≤n≤2×105, 1 ≤ Q ≤ 2 × 10 5 1 \le Q \le 2 \times {10}^5 1≤Q≤2×105, 1 ≤ k ≤ 3 1 \le k \le 3 1≤k≤3, 1 ≤ a i , b i ≤ n 1 \le a_i, b_i \le n 1≤ai,bi≤n, 1 ≤ s i , t i ≤ n 1 \le s_i, t_i \le n 1≤si,ti≤n, s i ≠ t i s_i \ne t_i si=ti。
测试点 n ≤ n \le n≤ Q ≤ Q \le Q≤ k = k = k= 特殊性质 1 1 1 10 10 10 10 10 10 2 2 2 是 2 2 2 10 10 10 10 10 10 3 3 3 是 3 3 3 200 200 200 200 200 200 2 2 2 是 4 ∼ 5 4 \sim 5 4∼5 200 200 200 200 200 200 3 3 3 是 6 ∼ 7 6 \sim 7 6∼7 2000 2000 2000 2000 2000 2000 1 1 1 否 8 ∼ 9 8 \sim 9 8∼9 2000 2000 2000 2000 2000 2000 2 2 2 否 10 ∼ 11 10 \sim 11 10∼11 2000 2000 2000 2000 2000 2000 3 3 3 否 12 ∼ 13 12 \sim 13 12∼13 2 × 10 5 2 \times {10}^5 2×105 2 × 10 5 2 \times {10}^5 2×105 1 1 1 否 14 14 14 5 × 10 4 5 \times {10}^4 5×104 5 × 10 4 5 \times {10}^4 5×104 2 2 2 是 15 ∼ 16 15 \sim 16 15∼16 10 5 {10}^5 105 10 5 {10}^5 105 2 2 2 是 17 ∼ 19 17 \sim 19 17∼19 2 × 10 5 2 \times {10}^5 2×105 2 × 10 5 2 \times {10}^5 2×105 2 2 2 否 20 20 20 5 × 10 4 5 \times {10}^4 5×104 5 × 10 4 5 \times {10}^4 5×104 3 3 3 是 21 ∼ 22 21 \sim 22 21∼22 10 5 {10}^5 105 10 5 {10}^5 105 3 3 3 是 23 ∼ 25 23 \sim 25 23∼25 2 × 10 5 2 \times {10}^5 2×105 2 × 10 5 2 \times {10}^5 2×105 3 3 3 否 特殊性质:保证 a i = i + 1 a_i = i + 1 ai=i+1,而 b i b_i bi 则从 1 , 2 , … , i 1, 2, \ldots, i 1,2,…,i 中等概率选取。
这道题的 k k k 很小,又是 多测 + dp
自然让我们想到动态dp!
考虑 k = 1 k = 1 k=1 的情况:
很简单,就是链上求和
f
u
=
f
v
+
val
u
f_{u} = f_v + \operatorname{val}_u
fu=fv+valu
考虑 k = 2 k = 2 k=2 的情况:
这个也不难想到,直接在链上跳,因为跳出链需要
2
2
2,跳进链也需要
2
2
2,然后的目的地和出发点也只有
2
2
2,非常的不值啊!
故有转移:(我们定义
f
x
,
i
f_{x,i}
fx,i 表示到达离
x
x
x 距离为
i
i
i 的点的代价)
f
u
,
0
=
min
(
f
v
,
0
,
f
v
,
1
)
+
val
u
f
u
,
1
=
f
v
,
0
\begin{align*} f_{u,0} &= \min(f_{v,0},f_{v,1}) + \operatorname{val}_u \\ f_{u,1} &= f_{v,0} \end{align*}
fu,0fu,1=min(fv,0,fv,1)+valu=fv,0
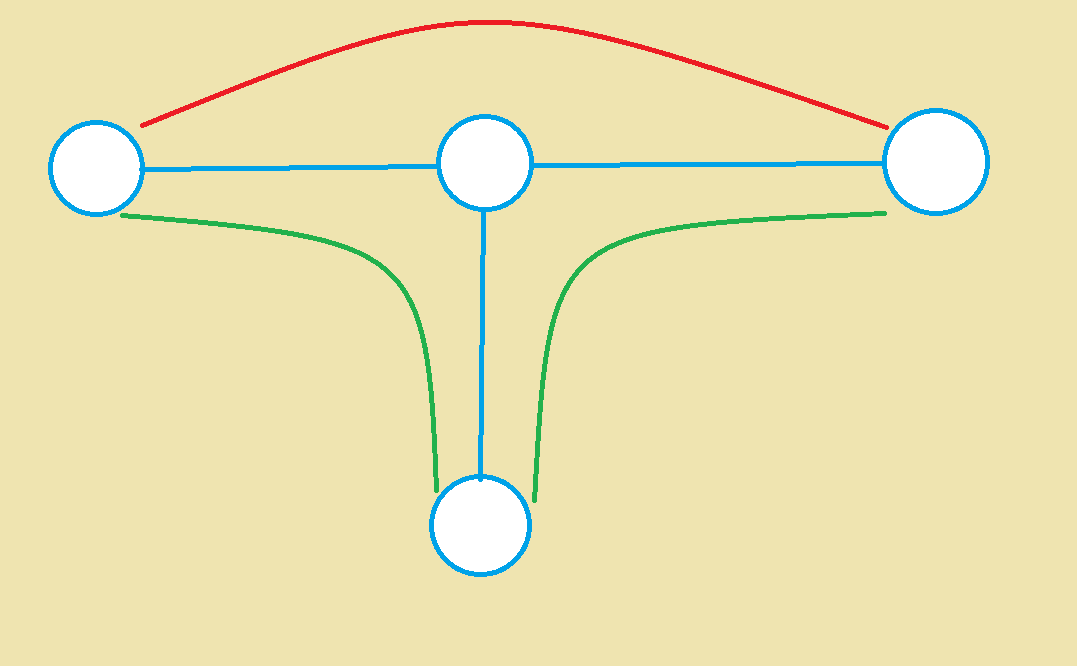
考虑 k = 3 k = 3 k=3 的情况:
这时情况略有不同,跳出链是否可行呢?
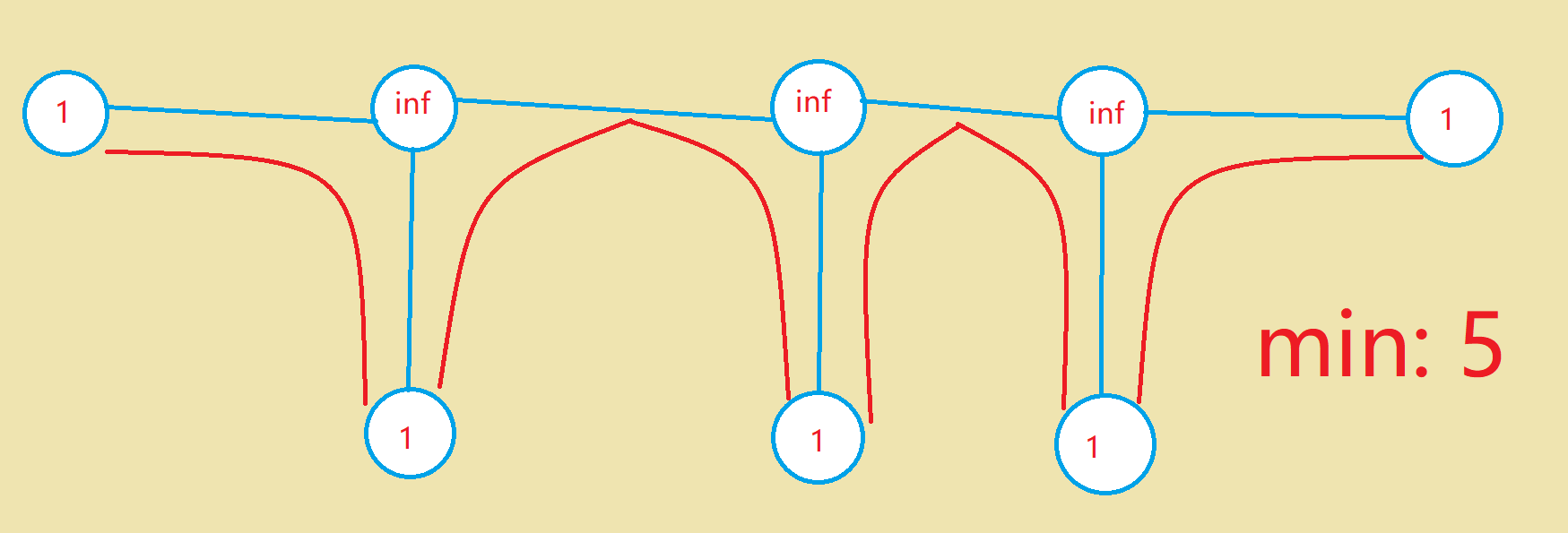
我们发现,跳出链可能更优秀!
有转移:
f
u
,
0
=
min
(
f
v
,
0
,
f
v
,
1
,
f
v
,
2
)
+
val
u
f
u
,
1
=
min
{
f
u
,
0
+
minn
u
min
(
f
v
,
0
,
f
v
,
1
)
+
minn
u
f
v
,
0
f
u
,
2
=
f
v
,
1
\begin{align*} f_{u,0} &= \min(f_{v,0},f_{v,1},f_{v,2}) + \operatorname{val}_u \\ f_{u,1} &= \min\begin{cases} f_{u,0} + \operatorname{minn}_u \\ \min(f_{v,0},f_{v,1}) + \operatorname{minn}_u \\ f_{v,0} \\ \end{cases} \\ f_{u,2} &= f_{v,1} \end{align*}
fu,0fu,1fu,2=min(fv,0,fv,1,fv,2)+valu=min⎩
⎨
⎧fu,0+minnumin(fv,0,fv,1)+minnufv,0=fv,1
这个 min \min min 里面套 min \min min 很烦人!
我们发现 f v , 0 + minn u > f v , 0 f_{v,0} + \operatorname{minn}_u > f_{v,0} fv,0+minnu>fv,0 !
而且, f u , 0 = min ( f v , 0 , f v , 1 , f v , 2 ) + val u f_{u,0} = \min(f_{v,0},f_{v,1},f_{v,2}) + \operatorname{val}_u fu,0=min(fv,0,fv,1,fv,2)+valu
所以, f u , 1 = min ( f v , 1 + minn u , f v , 0 , f v , 2 + val u + minn u ) f_{u,1} = \min(f_{v,1} + \operatorname{minn}_u,f_{v,0},f_{v,2} + \operatorname{val}_u +\operatorname{minn}_u) fu,1=min(fv,1+minnu,fv,0,fv,2+valu+minnu)
构造出矩阵:
k = 1 k = 1 k=1 时,
[ f v 0 0 ] × [ val u ∞ ∞ ∞ 0 ∞ ∞ ∞ 0 ] = [ f u 0 0 ] \begin{bmatrix} f_{v} & 0 & 0 \\ \end{bmatrix} \times\begin{bmatrix} \operatorname{val}_u & \infty & \infty \\ \infty & 0 & \infty \\ \infty & \infty & 0 \\ \end{bmatrix}=\begin{bmatrix} f_u & 0 & 0 \end{bmatrix} [fv00]× valu∞∞∞0∞∞∞0 =[fu00]
k
=
2
k = 2
k=2 时,
[
f
v
,
0
f
v
,
1
0
]
×
[
val
u
0
val
u
∞
]
=
[
f
u
,
0
f
u
,
1
]
\begin{bmatrix} f_{v,0} & f_{v,1} & 0 \end{bmatrix} \times \begin{bmatrix} \operatorname{val}_u & 0 \\ \operatorname{val}_u & \infty \\ \end{bmatrix} = \begin{bmatrix} f_{u,0} & f_{u,1} \end{bmatrix}
[fv,0fv,10]×[valuvalu0∞]=[fu,0fu,1]
k
=
3
k = 3
k=3 时,
[
f
v
,
0
f
v
,
1
f
v
,
2
]
×
[
val
u
0
∞
val
u
minn
u
∞
val
u
minn
u
+
val
u
0
]
=
[
f
u
,
0
f
u
,
1
f
u
,
2
]
\begin{bmatrix} f_{v,0} & f_{v,1} & f_{v,2} \end{bmatrix} \times \begin{bmatrix} \operatorname{val}_u & 0 & \infty \\ \operatorname{val}_u & \operatorname{minn}_u & \infty \\ \operatorname{val}_u & \operatorname{minn}_u + \operatorname{val}_u & 0 \\ \end{bmatrix} = \begin{bmatrix} f_{u,0} & f_{u,1} & f_{u,2} \end{bmatrix}
[fv,0fv,1fv,2]×
valuvaluvalu0minnuminnu+valu∞∞0
=[fu,0fu,1fu,2]
然后用树上倍增跑动态dp!
Tips : 本人对动态dp计算的误区——矩阵没有交换律!!!
为什么这个很重要呢?
看这段代码:
matrix<1,3> query(int x,int y) {
matrix<3,3> c;
for(int i = 0;i<3;i++) c[i][i] = 0;
while(top[x] ^ top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x,y);
c = c * sgt::query(1,1,n,id[top[x]],id[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y]) swap(x,y);
c = c * sgt::query(1,1,n,id[x],id[y]);
matrix<1,3> ans;
ans = ans * c;
return ans;
}
这个喜提
0
0
0 分,
因为他跳链计算的方式完全是乱的,但是这个广义矩阵乘法又没有交换律,故得出的答案也是完全错误!
而 P4719 这道题用树剖 + 线段树为什么是对的呢?
因为ta要求的答案是全局答案!并且修改的时候会对链头的父亲进行修改,而不是对整条链的修改!
而本题是一种类似于爬山的方式进行的矩阵乘法,如图:
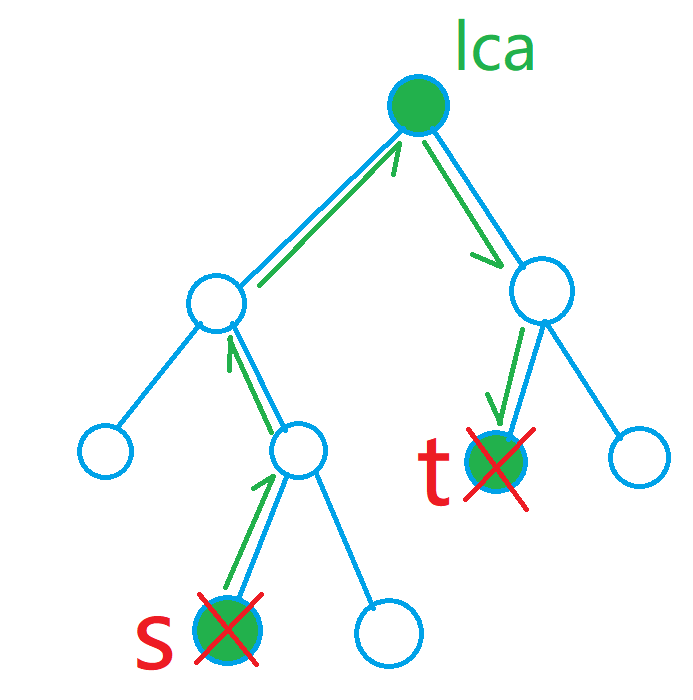
这个时候,我们考虑用树上倍增模拟这个爬山过程:
- 求出 lca ( s , t ) \operatorname{lca}(s,t) lca(s,t)
- 以上升的方式倍增求 mat 1 = ∏ i : [ s ∼ l c a ] [ val 0 ∞ val minn ∞ val minn + val 0 ] \operatorname{mat}_1 = \prod\limits_{i:[s \sim lca]} \begin{bmatrix} \operatorname{val} & 0 & \infty \\ \operatorname{val} & \operatorname{minn} & \infty \\ \operatorname{val} & \operatorname{minn} + \operatorname{val} & 0 \\ \end{bmatrix} mat1=i:[s∼lca]∏ valvalval0minnminn+val∞∞0
-
以下降的方式倍增求 mat 2 = ∏ i : [ l c a ∼ t ] [ val 0 ∞ val minn ∞ val minn + val 0 ] \operatorname{mat}_2 = \prod\limits_{i:[lca \sim t]} \begin{bmatrix} \operatorname{val} & 0 & \infty \\ \operatorname{val} & \operatorname{minn} & \infty \\ \operatorname{val} & \operatorname{minn} + \operatorname{val} & 0 \\ \end{bmatrix} mat2=i:[lca∼t]∏ valvalval0minnminn+val∞∞0
-
最后将答案 re = mat 1 × m a t [min{fa,minn}] × mat 2 \operatorname{re} = \operatorname{mat}_1 \times mat_{\operatorname{[min\{fa,minn\}]}} \times \operatorname{mat}_2 re=mat1×mat[min{fa,minn}]×mat2
答案就是 : r e 0 , 0 re_{0,0} re0,0
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define log2(x) __lg((x))
template<int N,int M,class T = long long>
struct matrix {
T m[N][M];
matrix(){memset(m,0x3f,sizeof(m));}
T* operator [] (const int pos) {return m[pos];}
};
template<int N,int M,int R,class T = long long>
matrix<N,R,T> operator * (matrix<N,M,T> a,matrix<M,R,T> b) {
matrix<N,R,T> c;
for(int i = 0;i<N;i++)
for(int j = 0;j<M;j++)
for(int k = 0;k<R;k++)
c[i][k] = min(c[i][k],a[i][j] + b[j][k]);
return c;
}
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
const int N = 2e5+5,inf = 0x3f3f3f3f3f3f3f3fLL;
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
int n,q,k,v[N],minn[N];
int head[N],nxt[N<<1],to[N<<1],cnt;
void init() {
memset(head,-1,sizeof(head));
cnt = 0;
}
void add(int u,int v) {
nxt[cnt] = head[u];
to[cnt] = v;
head[u] = cnt++;
}
int fa[19][N],dep[N];
matrix<3,3> down[19][N],up[19][N];
matrix<3,3> get(int id,int fav = inf) {
matrix<3,3> c;
switch(k) {
case 1:
c[0][0] = v[id];
break;
case 2:
c[0][1] = 0;
c[0][0] = c[1][0] = v[id];
break;
case 3:
c[0][0] = c[1][0] = c[2][0] = v[id];
c[1][1] = min(minn[id],fav);
c[2][1] = min(minn[id],fav) + v[id];
c[0][1] = c[1][2] = 0;
break;
}
return c;
}
void dfs(int x,int f){
fa[0][x] = f;
dep[x] = dep[f] + 1;
minn[x] = inf;
for(int i = head[x];~i;i = nxt[i]) {
int y = to[i];
if(y ^ f) {
dfs(y,x);
minn[x] = min(minn[x],v[y]);
}
}
down[0][x] = up[0][x] = get(x);
}
matrix<1,3> f;
int lca(int x,int y) {
if(dep[x] < dep[y]) swap(x,y);
int d = dep[x] - dep[y];
for(int j = 18;j >= 0;j--) if(d >> j & 1) x = fa[j][x];
if(x == y) return x;
for(int j = 18;j >=0;j--) if(fa[j][x] ^ fa[j][y]) x = fa[j][x],y = fa[j][y];
return fa[0][x];
}
matrix<3,3> getDown(int u,int k) {
matrix<3,3> re;
for(int i = 0;i<3;i++) re[i][i] = 0;
for(int j = 18;j >= 0;j--) if(k >> j & 1) re = down[j][u] * re,u = fa[j][u];
return re;
}
matrix<3,3> getUp(int u,int k) {
matrix<3,3> re;
for(int i = 0;i<3;i++) re[i][i] = 0;
for(int j = 18;j >= 0;j--) if(k >> j & 1) re = re * up[j][u],u = fa[j][u];
return re;
}
int query(int s,int t) {
int LCA = lca(s,t);
matrix<1,3> re = f * getUp(s,dep[s] - dep[LCA]) * get(LCA,v[fa[0][LCA]]) * getDown(t,dep[t] - dep[LCA]);
return min({re[0][0] - v[t],re[0][1],re[0][2]}) + v[t];
}
signed main() {
init();
n = rd(),q = rd(),k = rd();
f[0][k - 1] = 0;
v[0] = inf;
for(int i = 1;i<=n;i++) v[i] = rd();
for(int i = 1;i<n;i++) {
int u = rd(),v = rd();
add(u,v);add(v,u);
}
dfs(1,0);
for(int j = 1;j<=18;j++) {
for(int i = 1;i<=n;i++) fa[j][i] = fa[j - 1][fa[j - 1][i]];
for(int i = 1;i<=n;i++) down[j][i] = down[j - 1][fa[j - 1][i]] * down[j - 1][i];
for(int i = 1;i<=n;i++) up[j][i] = up[j - 1][i] * up[j - 1][fa[j - 1][i]];
}
while(q--) {
int s = rd(),t = rd();
wt(query(s,t));
putchar('\n');
}
return 0;
}






















 1970
1970

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








