RMSNorm原理详解

最新推荐文章于 2025-09-30 15:06:46 发布

原创最新推荐文章于 2025-09-30 15:06:46 发布 · 292 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#大模型 #机器学习 #transformer

大模型专栏收录该内容

56 篇文章

订阅专栏

背景和动机

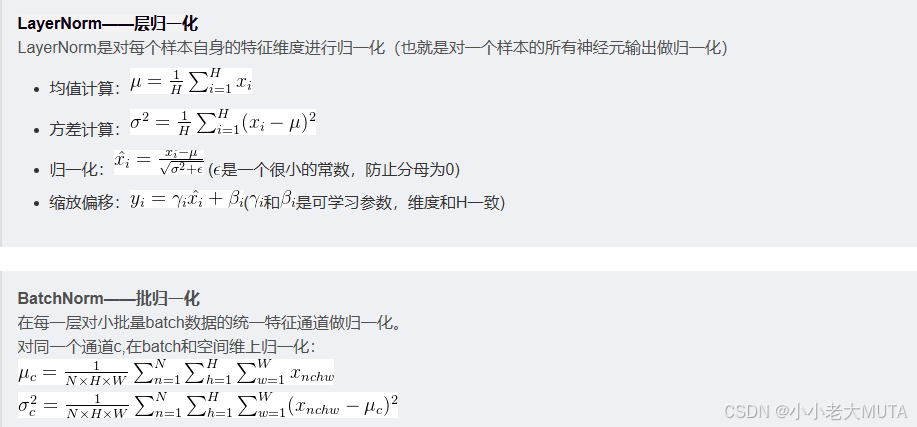
深度学习网络训练中，归一化Normalization 大大提升了训练稳定性和收敛速度，例如LayerNorm 和BatchNrom。

在Transformer中，使用的是LayerNorm对单个样本的所有特征维度做均值和方差归一化。

但是在LayerNorm计算中，包含均值和标准差的计算（涉及到平方、开方），且还有两个参数（scale 和 bias）进行仿射变换。

RMSNorm是一种轻量的归一化方案，最终目的是保持归一化效果的同时，减少计算开销和参数量。

Transformer内容详解（通透版）-CSDN博客

原理

假设输入向量为x=[x1,x2,...,xd](这里指网络某一层单个样本的特征维度)

1. 计算均方根RMS:

$RMS(x) = \sqrt{\frac{1}{d}\sum_{i-1}^{d}{x_i}^2}$

2. 归一化操作：用RMS代替LayerNorm中的均值和标准差进行归一化

$\hat{x} = \frac{x}{RMS(x)+\epsilon }$

$\epsilon$ 是一个很小的数，防止除0。

3. 缩放scale

$y_i = g_i \cdot \hat{x_i}$

通常没有偏置项bias,因为去除均值后，偏置的作用减小。

为什么去掉均值？

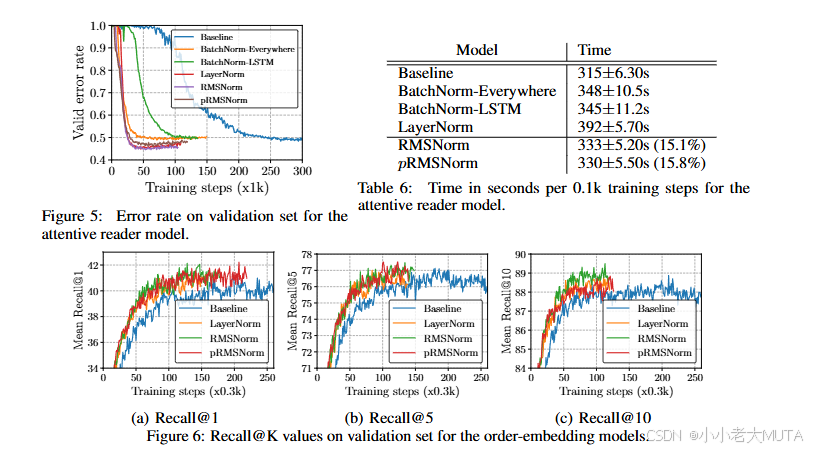
作者实验证明，去除均值计算并不会显著损害模型性能，反而降低了计算开销。

从理论上解释，因为均值的作用主要是把分布中心化，但网络的非线性和后续层的偏置参数等，也能补偿这一点。

代码

import torch
import torch.nn as nn

class RMSNorm(nn.Module):
    def __init__(self, dim, eps=1e-8):
        """
        RMSNorm实现
        :param dim: 输入特征的维度大小
        :param eps: 防止除零的小常数
        """
        super().__init__()
        self.eps = eps
        self.scale = nn.Parameter(torch.ones(dim))  # 可训练的缩放参数g

    def forward(self, x):
        # x的形状通常是 [batch_size, ..., dim]
        # 计算均方根（RMS）
        rms = x.pow(2).mean(dim=-1, keepdim=True).sqrt()  # shape: [..., 1]
        x_normed = x / (rms + self.eps)                   # 归一化操作
        return self.scale * x_normed                       # 乘以缩放参数

# 测试示例
if __name__ == "__main__":
    x = torch.randn(2, 3, 4)  # 例如形状为(batch=2, seq=3, dim=4)
    rmsnorm = RMSNorm(dim=4)
    y = rmsnorm(x)
    print(y)