Attention为什么要除以根号d

李学的博客

于 2024-06-09 19:08:44 发布

阅读量1.2k

点赞数 24

文章标签：人工智能机器学习深度学习

本文链接：https://blog.csdn.net/qq_50988647/article/details/139562650

版权

我们知道，attention 结构中注意力得分的计算公式为 $Attention(Q,K,V)) = softmax(\frac{QK^T}{\sqrt{d}})$ ，其中 $Q,K,V,d$ 分别表示 $query,key,value$ 及其维度，那么为什么在计算score的时候要除以 $\sqrt{d}$ 呢？这个问题比较考验各位同学的数学功底，我将从自己理解的角度进行分析，欢迎大家评论指正。

已有结论

在《Attention is All Your Need》的原始论文中，作者对这个问题给出一个比较粗略的答案

While for small values of the two mechanisms perform similarly, additive attention outperforms dot product attention without scaling for larger values of [3]. We suspect that for large values of, the dot products grow large in magnitude, pushing the softmax function into regions where it has extremely small gradients . To counteract this effect, we scale the dot products by $\frac{1}{\sqrt{d}}$ .

简而言之就是当维度 $d$ 的值变大的时候，softmax函数会造成梯度消失，所以设置了一个 softmax 的scale来缓解这个问题，原文中的 scale 设置成了 $\sqrt{d}$ 。但是由此衍生出来的以下两个问题作者并没有进一步解释：

1. 当维度 $d$ 的值变大的时候，为什么 softmax 函数会造成梯度消失？

2. scale 除了 $\sqrt{d}$ 外还有更优的值吗？

维度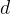 $d$ 变大为什么会导致梯度消失

先说明一下推导结论：

1. 如果 $d$ 变大，那么 $Q\cdot K^{T}$ 的方差也会变大。

2. $Q\cdot K^{T}$ 的方差变大会导致向量之间元素的差值变大。

3. 元素的差值变大会导致 softmax 退化为 argmax ，也就是 softmax 后向量的元素中只有一个等于1，其余都是0。

4. 若 softmax 后只有一个元素为非0值，那么反向传播的梯度就都会变成0，导致模型参数无法更新，也就是梯度消失。

分别对以上4点进行数学证明。

1. 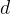$d$ 变大，那么 $Q\cdot K^{T}$ 的方差也会变大

先假设 Q 和 K 都是方差为1，均值为0的向量，并且长度都为 d。那么 Q 和 K 的点积的方差为：

$var[Q\cdot K^{T}] \\\\= var[\sum_{i=1}^{d}Q_{i}\cdot K_{i}]\\\\ =\sum_{i=1}^{d}var[Q_{i}\cdot K_{i]}\\\\=sum_{i=1}^{d}var[Q_{i}]\cdot var[K_{i}]\\\\=sum_{i=1}^{d}1\cdot 1\\\\=d$

可以看到在此假设下 Q 和 K 的方差就等于 d，所以当维度 d 变大时，方差也会跟着一起变大

2. 方差变大会导致向量之间元素的差值变大

方差变大显而易见就是代表数据之间的差异性变大了，那如何通过数学手段对此进行证明呢？我们可以通过换一个问题从侧面回答这个问题：假设向量是通过独立同分布采样出来的 n 个数据，那么这 n 个数的最大值的期望是多少呢？我这里仍然选用最常用的正态分布来证明。

2.1 期望值上界推导

首先假设 X 服从标准正态分布，即 $X_{i}\sim N(0,1), M_{n}=max_{1\leqslant i\leqslant n}X_{i}$ 。根据极值理论，可以推导得到 $M_{n}$ 得期望值为：

$E|M_{n}|\approx \sqrt{2\cdot logn}$

由此可以得到一般正态分布的最大值。假设 $Z_{i}\sim N(0,\sigma ^2)$ ，可以将其视为 $Z_{i}=\sigma \cdot X_{i}$

$Y=max_{1\leqslant i \leqslant n}Z_{i}=\sigma \cdot max_{1\leqslant i \leqslant n}X_{i}=\sigma \cdot M_{n}$

由此可以得到期望值的上界

$E|Y|\approx \sigma\sqrt{2\cdot logn}$

2.2 期望值下界推导

对于 $Z_{i}\sim N(0,\sigma ^2)$ ，其累积分布函数（CDF）为：

$F_{Z}(z)=\phi (\frac{z}{\sigma})$ ，其中 $\phi$ 是标准正态分布的 CDF。

那么最大值 Y 的 CDF 为：

$F_{Y}(y)=[\phi (\frac{y}{\sigma})]^n\\\\ E[Y]=\int_{}^{}yf_{Y}(y)dy$

其中 $f_{Y}(y)$ 是 Y 的概率密度函数（PDF），由 F_{Y}(y) 求导得到：

$f_Y(y)=\frac{\mathrm{d} F_{Y}(y)}{\mathrm{d} z}=n[\phi(\frac{y}{\sigma})]^(n-1)\cdot\phi_1(\frac{y}{\sigma})\cdot\frac{1}{\sigma}$

其中 $\phi_1$ 是标准正态分布的 PDF。综合极值理论，可以近似得到：

$E|Y|=\sigma\cdot\sqrt{2log n}-\frac{\sigma(logn+log4\pi)}{2\sqrt{2logn}}$

论文中经过近似后给的下界为：

$E[max_{1\leqslant i \leqslant n}Z_{i}]\geqslant \frac{\sigma}{\sqrt{\pi log2}}\sqrt{logn}$

综上所述，我们最终可以得到如下不等式：

$\frac{\sigma}{\sqrt{\pi log2}}\sqrt{logn} \leq E|Y| \leq \sigma\sqrt{2\cdot logn}$

从上式中的下界可以看出，随着方差的变大，最大值的期望也会跟着变大。正态分布的最小值就是最大值的相反数，因此可以证明方差变大时向量元素之间的差值也变大了。

3. softmax 退化为 argmax

softmax 函数的计算公式为：

$y_{i}=softmax(x_{i})=\frac{e^{x_{i}}}{\sum_{j=1}^{n}e^{x_{j}}}$

当 $x_{k}$ 是最大的元素时， $e^{x_{k}}$ 会显著大于其余 $e^{x_{i}}$ ，因此当且仅有 $i=k$ 时 softmax 值才为非0值，此时 softmax 就退化为了 argmax。下面用代码演示一下

import numpy as np

n = 20
def softmax(x):
    return np.exp(x) / np.sum(np.exp(x), keepdims=True)

x1 = np.random.normal(loc=0, scale=1, size=n)
x2 = np.random.normal(loc=0, scale=np.sqrt(1024), size=n)

print('x1最大值和最小值的差值:', max(x1) - min(x1))
print('x1最大值和最小值的差值:', max(x2) - min(x2))

soft1 = softmax(x1)
soft2 = softmax(x2)
print('softmax(x1) =', soft1)

print('softmax(x2) =', soft2)

x1最大值和最小值的差值:3.473771214845455
x2最大值和最小值的差值:115.85095739600229
('softmax(x1) =', array([0.02470037, 0.1853221 , 0.06719284, 0.02643318, 0.00741414,
       0.2391664 , 0.03484815, 0.03331956, 0.02722814, 0.07514086,
       0.01541654, 0.05519453, 0.03836135, 0.02359709, 0.01004924,
       0.01541326, 0.01339333, 0.02061181, 0.03638033, 0.05081677]))
('softmax(x2) =', array([1.62212649e-23, 3.95375402e-11, 1.10795601e-01, 2.51717170e-39,
       1.77253286e-10, 4.31994570e-51, 6.62804927e-39, 1.46486437e-27,
       1.46763464e-34, 2.01937638e-12, 1.86328705e-20, 3.00182725e-39,
       2.80124955e-11, 4.90632311e-30, 1.87925439e-04, 6.92457667e-19,
       1.51435108e-22, 8.89016472e-01, 7.43235548e-19, 1.77750861e-09]))

可以看到当方差为1是，softmax 各元素之间差异不是很大；当方差增大到 np.sqrt(1024) 时，softmax 只有一个元素（0.889）接近1，其余都几乎为0。

4. softmax 为什么会导致梯度消失

对 softmax 公式求导（这个比较简单，我这里就直接给结论了）：

$when\ i=k:\\ \\ \frac{\mathrm{d} y_{i}}{\mathrm{d} x_{i}}=y_{i}\cdot (1-y_{i})\\\\ when\ i!=k:\\\\ \frac{\mathrm{d} y_{i}}{\mathrm{d} x_{i}}=-y_{i}\cdot y_{k}$

将两种情况合并起来即得：

$\frac{\mathrm{d} y_{i}}{\mathrm{d} x_{i}}=y_{i}\cdot (\delta_{ik} - y_{i})\\\\ \delta_{ik} = \begin{cases} 1 & \text{ if } i=k \\ 0 & \text{ if } i!=k \end{cases}$

最终可以用 Jacobian 矩阵表示，Jacobians 矩阵的第 i 行和第 j 列元素是 $\frac{\mathrm{d} y_{i}}{\mathrm{d} x_{i}}$ ：

$J=\begin{bmatrix} y_{1}(1-y_{1}) &-y_{1}y_{2} &....... &-y_{1}y_{n} \\ -y_{2}y_{1}&y_{2}(1-y_{2}) &....... &-y_{2}y_{n} \\ ...&... &... &... \\ -y_{n}y_{1}&y_{n}(1-y_{2}) &....... &-y_{n}(1-y_{n}) \end{bmatrix}$

结合上面三步的证明，有意思的事情发生了。当方差变大时，softmax 退化成了只有一个值不为0的向量，将这个向量带入上面的 Jacobian 矩阵发现对任意的 $y_{k}=1,y_{j!=k}=0$ 的向量来说，Jacobian 矩阵变成了一个全0矩阵，也就是说梯度消失了。下面仍然用代码演示一下：

import numpy as np

n = 20
def softmax(x):
    return np.exp(x) / np.sum(np.exp(x), keepdims=True)

def softmax_grad(y):
    return np.diag(y) - np.outer(y, y)

x1 = np.random.normal(loc=0, scale=1, size=n)
x2 = np.random.normal(loc=0, scale=np.sqrt(1024), size=n)

soft1 = softmax(x1)
soft2 = softmax(x2)

print('x1最大值和最小值的差值:', max(x1) - min(x1))
print('x1最大值和最小值的差值:', max(x2) - min(x2))

print('softmax(x1) =', soft1)
print('softmax(x2) =', soft2)

print('max of gradiant of softmax(x1) =', np.max(softmax_grad(ex1)))
print('max gradiant of softmax(x2) =', np.max(softmax_grad(ex2)))

x1最大值和最小值的差值:3.671594098604443
x1最大值和最小值的差值:173.75440652168083

('softmax(x1) =', array([0.02007988, 0.02258829, 0.03580352, 0.00635528, 0.07158731,
       0.00884057, 0.05542608, 0.02338228, 0.0176709 , 0.04382125,
       0.01101102, 0.24985466, 0.0676969 , 0.01331248, 0.00777607,
       0.04515762, 0.16042938, 0.02530876, 0.09323235, 0.02066542]))

('softmax(x2) =', array([2.30464604e-46, 1.08831204e-60, 1.84173070e-52, 3.46274126e-76,
       2.08945145e-44, 1.17607261e-36, 1.93672935e-49, 1.26526171e-37,
       6.36817775e-62, 2.18779237e-60, 4.06001854e-63, 1.43342792e-30,
       4.84948070e-36, 2.13555102e-28, 8.59106456e-73, 5.11784352e-35,
       1.00000000e+00, 6.90781471e-52, 2.61753870e-45, 2.11786363e-55]))

('max of gradiant of softmax(x1) =', 0.1874273066304809)
('max gradiant of softmax(x2) =', 2.135551017312488e-28)

可以看到方差为1时，softmax 回传梯度还是比较正常的；而当方差为 np.sqrt(1024) 时，回传梯度已经全部为0了。

scale 除了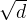 $\sqrt{d}$ 外还有更优的值吗？

这个问题在上面的证明过程中其实已经有过阐述了。当 scale 除 $\sqrt{d}$ 后，就可以将 $Q\cdot K^{T}$ 归一化成一个服从标准正态分布的向量。从熵不变性来看 scale 除 $\sqrt{d}$ 的确是目前最优的值了。大家如果感兴趣可以看看熵不变性看Attention的Scale操作

李学的博客

关注

24
点赞
踩
18

收藏

觉得还不错? 一键收藏
1
评论
Attention为什么要除以根号d

我们知道，attention结构中注意力得分的计算公式为，其中分别表示及其维度，那么为什么在计算score的时候要除以呢？这个问题比较考验各位同学的数学功底，我将从自己理解的角度进行分析，欢迎大家评论指正。
复制链接

扫一扫