2021-06-07 傅里叶变换之你死我活

参考文章：

https://blog.csdn.net/weixin_39504171/article/details/94553357

一、傅里叶

        傅里叶：让·巴普蒂斯·约瑟夫·傅里叶（Baron Jean Baptiste Joseph Fourier，1768年3月21日-1830年5月16日），法国欧塞尔人，著名数学家、物理学家。

        傅里叶是一位法国数学家和物理学家的名字，于1807年在法国科学学会上发表了一篇论文，运用正弦曲线来描述温度分布，也就是说傅里叶变换是应用在热物理领域，论文里有个在当时具有争议性的决断：任何连续周期信号可以由一组适当的正弦曲线组合而成。

        当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日和拉普拉斯，当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在他此后生命的六年中，拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，拒绝了傅里叶的工作，幸运的是，傅里叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。（名人一般都是死后才有的名）

        在一定程度上，拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，当我们学了极限之后，利用逼近的思想，我们可以用正弦曲线来非常逼近棱角信号，逼近到两种表示方法不存在能量差别，基于此，傅里叶是对的。

        第一次接触傅里叶及傅里叶变换是在大学的课堂上，当时心思没在学习上没有继续深究，现在在读研很不幸我又遇到了他，既然躲不掉我就想和他battle一下。总而言之他也是个人，就长下边的这个样子，不一定有你好看，没有好怕的，他能会的大家都可以会，就是多花些时间的问题嘛！就像这是我写的第一篇CSDN文章一样，前两天在课上单片机老师说了一句话我十分认同：谁也不是生下来就什么都会的！

二、傅里叶变换

        前面介绍了傅里叶，下边再介绍一下他的作品，傅里叶是他的名字，傅里叶变换是他的作品，但是变换是什么意思？变换是变换的什么？名字是一件事物的外表，就算是数学公式他也不会乱起名字，把内在的含义理解透了也就知道他为什么折磨起名字了。

        傅里叶变换原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

       和傅里叶变换算法对应的是反傅里叶变换算法。该反变换从本质上说也是一种累加处理，这样就可以将单独改变的正弦波信号转换成一个信号。因此，可以说，傅里叶变换将原来难以处理的时域信号转换成了易于分析的频域信号（信号的频谱），可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅里叶反变换将这些频域信号转换成时域信号。

       傅里叶变换中的变换就是实现时域空间向频域空间的转换，发挥你的想象力，把大家的生活由按照时间走，转换为按照频率走，说到这里你可能还不太明白，闲言少叙，ing。

三、时域与频域

       不知道名字的某位伟人曾经说过，通过频域空间来观察世界的话，你会发现世界是永恒不变的。第一次看见的时候我脑子里有一万个为什么？为什么？为什么？

        从我们出生，我们看到的世界都以时间贯穿，股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。那么时域是什么？时域就是以时间为变量的空间，简单表示为一个二维坐标系，横坐标是不断前进的时间。为了更通俗一点，在一维空间内，以声音为例证：

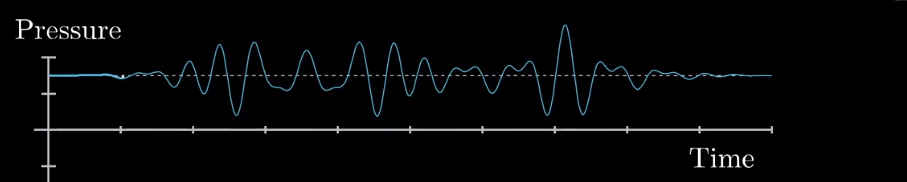
        这是我们通过传感器获取的一段声音音频，此坐标系横轴代表时间，纵轴代表声强（声波的能量），通过图片我们可以很容易的看出，声音强度会随着时间的变化不断变化，就像我们的生活一样，一切都是随着时间的发展不断变化，每一秒每一秒不断发展变化，如果用一个波形图来表示我们的生活，很自然的想象一下，他会杂乱无章，就像上边的这个音频图一样，在这个坐标系内他几乎没有什么规律。

       傅里叶的伟大之处，能让这么多学子对他都咬牙切齿的原因，就在于他在这个杂乱无章的波形图里边发现了规律。他将时域空间中的波形图通过数学计算的方法转换到频域空间中，有同学的同学又要问了，什么是频域？频域就是频率的空间，这是句废话，对你理解没有帮助。

        通过傅里叶变换，将上边杂乱无章的波形图，转换为不同频率的正弦波信号的无限叠加。如下图所示，一个声音波形图是由不同频率的几个正弦波叠加而成的。从事声音处理相关方向的学者，利用傅里叶变换将一段波形分解为n个不同频率的正弦波，从而对不同频率的声波就行处理获得自己想要的信息，例如去除一定频率的杂音或者进行声音识别等等。

两种声音合成，在任意时刻声强的变化就是每种声调产生的压强的总和，增强与抵消都会发生：

+

||

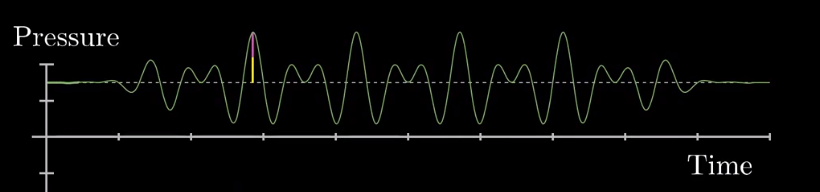
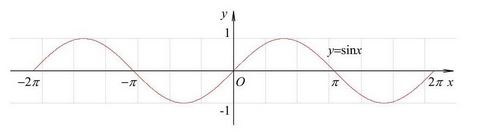
        说到这里，没有介绍傅里叶变换的公式，因为我认为理解底层的含义更加重要，到这里你应该理解了傅里叶就是找到了一个数学工具将杂乱无章的声波分解为不同频率的多个声波，多个声波相互叠加就形成了复杂的平常生活中的波形。而频域就是将横坐标时间，转换为频率，用来表示不同频率的正弦波，例如下边这种形式：

 

        在时域来看呢就是随时间不断变化的波形图，在频域来看呢，就可以理解为一个杂乱无章的波形图可以又n个不同频率的正弦波组成，而频域呢就是为了表示不同频率的正弦波而设计的一个空间，在右边的这个图里横坐标是频率，纵轴表示频幅，我个人认为只是这样表示起来更加简洁明了，说到这里就没有什么复杂难理解的内容了：傅里叶将复杂波形图由时域转换到频域，就是将一个复杂的波形，分解为n个不同频率的正弦波，为了便于表示这些正弦波就创建了频域，用频域来表示一个复杂的波形是由频率和幅值多大的正弦波组成的。

 

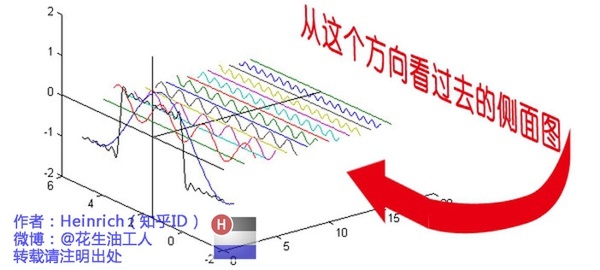
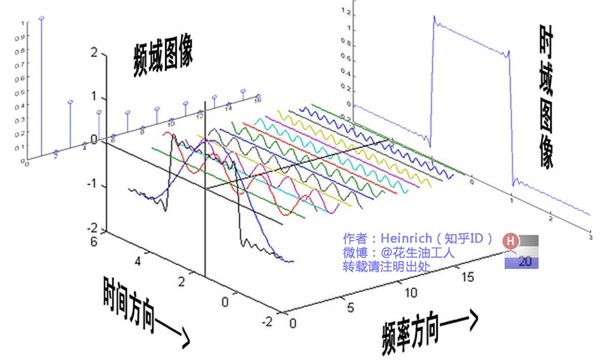
四、二维空间（图像）

        在上面介绍了一维声音的波形图，下面我们继续谈谈更加复杂的二维图像是如何进行傅里叶变换的，先看一下下边的图片。

        利用傅里叶变化将二维图像转换为频谱图，在刚开始看的时候我是真的蒙了，右边这个图是个什么鬼啊，我们先来了解一下频谱图。

频谱图简介:

       图像二维频谱图通过对输入图像进行水平和竖直两个方向的所有扫描线的一维傅立叶变换进行叠加得到,用来表示输入图像的频率分布。从事图像处理方向的同学应该清楚数字图像是又一个个紧密排列的像素点构成的，我们将离散的二维像素点从水平和竖直方向分别进行曲线拟合然后就可以获得复杂的波形图，利用上边讲的一维波形图分解的原理将拟合的波形图分解为不同的频率的正弦波，整幅图像从水平和竖直方向都进行扫描，获得了不同的频率、振幅、相位的正弦波。

      为了表示二维图像，不知道谁有发明了频谱图，和一维的频域类似都锻炼大家的空间想象力，我将其理解为一个只有频域没有时间，舍弃掉时间单位，以频率为计量单位的一个二维空间，在频谱图中以图像的中心为圆心,整幅图像由n个圆组成.圆上一点的相位对应原图中频率分量的相位,半径对应频率高低。低频半径小,高频半径大,中心为直流分量,某点的灰度值对应该频率的能量高低。波的能量与振幅成正比，即频谱图表示了不同正弦波的频率、相位及能量（振幅）。

频谱图的特征:

①在频谱图中,中心部分(u-v坐标系中点(0.0)附近)表示原图像中的低频部分。 

②如果原始图像具有十分明显的规律,在频谱图中也会有一定的规律。

③如果频谱图中暗的点数更多,那么实际图像是比较柔和的(各点与邻域差异都不大,梯度相对较小) ;反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的(边界分明且边界两边像素差异较大)。

④频谱图中心对称,并且将一张灰度图像反相后,其频谱样式不变。

⑤频谱图上的各点与图像上各点并不存在-对应的关系,频谱上每一点都与空域所有点有关,反之,空域每一点都与频谱上所有只有关。

(3)频谱图的表示：频谱图中的横纵坐标分别表示输入图像在横纵坐标的空间频率。

①一张全黑的图,频谱图为全黑。（图像无灰度变化,全部为黑色因此也无能量)

 ②一张灰色的图,频谱图表现为一个在中心上的单像素白色方块。(图像无灰度变化,因此能量集中在0频率点上)

③一张全白的图,频谱图表现为一个在中心上的单像素白色方块,方块能量值大于上面灰色图像频谱图的能量。（图像无灰度变化,因此能量集中在0频率点上)

        换一种更加宏观的角度去理解，一共有n张类似于下图的正弦图像，不同角度不同频率不同幅值，一张正弦图片可以由一对频谱点表示，频谱点距离表示频率，角度表示正弦图片的角度，灰度值表示幅值。与一维信号类似，二维图片也可以用多张不同方向和频谱的正弦图叠加表示。

        了解基本的傅里叶变换操作后，我们就可以对图像先进行傅里叶变换，然后在频率域上进行滤波操作后，再利用傅里叶逆变换得到处理之后的图像，利用低通滤波实现图像平滑处理。

        这是本学渣写的第一篇文章，没有去深究数学公式的推导，个人认为底层的只要底层思想明白了，数学公式应该不会有太大问题，毕竟我不是数学专业，会用就可以啦，有什么问题和错误希望大家不吝赐教！祝大家学业快乐！