[专业课]——数据结构&算法复习(1h)

木子一个Lee

已于 2023-08-02 18:01:23 修改

阅读量287

点赞数

分类专栏：保研升学数据结构文章标签：数据结构算法

于 2023-07-18 20:05:58 首次发布

原文链接：https://blog.csdn.net/jokerxsy/article/details/117433117

版权

数据结构同时被 2 个专栏收录

7 篇文章 5 订阅

订阅专栏

保研升学

6 篇文章 1 订阅

订阅专栏

排序

排序的分类:

稳定\不稳定
内部\外部

插入排序

直接插入排序

在这里插入图片描述
时间复杂度:O(n2)
空间复杂度:O(1)
稳定
内部

折半插入排序

在这里插入图片描述
时间复杂度:O(n2)(二分查找的过程只是减小了比较的次数，移动次数依然不变，所以还是O(n2))
空间复杂度:O(1)
稳定
内部

希尔排序

把元素按照下标的增量分组，组内用直接插入排序。增量较大时，使得元素能够大幅度的移动，解决了直插中大量移动的问题；增量减小到1时，变为直接插入排序，此时序列已经大致有序，只需简单微调即可完成。
在这里插入图片描述
时间复杂度:跟步长有关，O(n1.5)(最坏) O(nlogn)(最好)
空间复杂度:O(1)
不稳定
内部

交换排序

冒泡排序

在这里插入图片描述
时间复杂度:O(n2)
空间复杂度:O(1)
稳定
内部

快速排序

取首元素为基准元素，定义low指针和high指针。先从high指针出发，从右往左依次比较，如果当前high指针指向元素小于基准元素，则把该元素赋值到low指针所在位置，然后切换到low指针，开始从左往右依次比较；一旦low指针和high指针重合，就把基准元素赋到该位置，然后递归进行左右子数组的快排。
在这里插入图片描述
时间复杂度:O(nlogn)
空间复杂度:O(logn)
不稳定
内部

选择排序

直接选择排序

直接选择每一次都在乱序中依次比较，没有利用好上一次比较得到的部分信息，树形选择排序是对它的改进。
在这里插入图片描述
时间复杂度:O(n2)
空间复杂度:O(1)
不稳定
内部

树形选择排序

树形选择排序为什么是稳定的？–>对于左右孩子结点相同的情况，取坐标的元素作为它们的父亲结点即可。
树形选择排序是一个稳定的外部排序，堆排序针对此做了改进，但它变成了不稳定的。
如果待比较结点个数是奇数个，则最后一个结点直接”晋级“
在这里插入图片描述

时间复杂度:O(nlogn)
空间复杂度:O(n)(2n-1)
外部
稳定

堆排序

升序->大顶堆（a[i] > max(a[ix2+1], a[ix2+2])），降序->小顶堆。
【从1开始编号！->arr.length/2】在初始化堆时，因为是完全二叉树，1. 只存在n0和n2，又n0=n2+1，所以最后一个非叶子结点是第arr.length/2个结点；2. 只存在n0、n2和唯一一个n1，又n0=n2+1，所以最后一个非叶子结点是第arr.length/2个结点
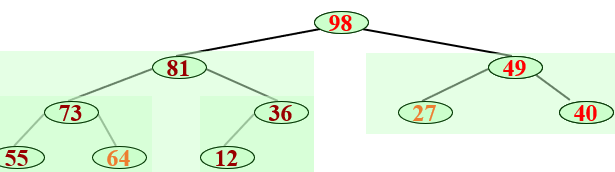
在这里插入图片描述
时间复杂度:O(nlogn)
大顶堆构建的时间复杂度: O(n)
空间复杂度:O(1)
内部
不稳定

归并排序

在这里插入图片描述
时间复杂度:O(nlogn)
空间复杂度:O(n)
外部
稳定

查找

基于静态表的查找

顺序查找

在这里插入图片描述
无序表
O(n)

折半查找

在这里插入图片描述
顺序表
O(logn)

索引查找

在这里插入图片描述
块间有序，块内可以无序，复杂度位于顺序查找和二分查找之间

基于动态表的查找

二叉查找树

查找

时间复杂度:依赖于二叉树的拓扑结构，最好O(logn) 最差O(n)
插入：同查找
删除：
- 删除叶子节点，删！
- 删除只有单侧子树的非叶子节点，父节点的单侧子树 = 删除节点的单侧子树
- 删除既有左也有右的非叶子节点，找到中序遍历的前驱(比它小的里面最大的)
  - 删除节点的左孩子(1)没有右孩子：删除节点的左孩子 = 删除节点的左孩子的左孩子，删除节点改值(1)
  - 删除节点的左孩子拥有右孩子：删除节点的左孩子的最右孩子(2)的父亲的左孩子 = 删除节点的左孩子的最右孩子的左孩子，删除结点改值(2)

二叉平衡树

任意一个结点的左右子树高度差不超过1

查找:O(logn)
插入: 插入之后，需要判断是否不平衡。如果不平衡，有左左、右右、左右、右左

四种调节方式:

左左:不平衡节点右转(不平衡节点的左孩子代替之，不平衡节点的新左孩子为其左孩子的右子树)
右右:不平衡节点左转(不平衡节点的右孩子代替之，不平衡节点的新右孩子为其右孩子的左子树)
左右:不平衡节点的左孩子先左转，成为左左，再右转
右左:不平衡节点的右孩子先右转，成为右右，再左转

删除:

删除叶子节点，删！
删除只有单侧子树的非叶子节点，父节点的单侧子树 = 删除节点的单侧子树
删除既有左也有右的非叶子节点，找到中序遍历的前驱
- 删除节点的左孩子(1)没有右孩子：删除节点的左孩子 = 删除节点的左孩子的左孩子，改值(1)
- 删除节点的左孩子拥有右孩子：删除节点的左孩子的最右孩子(2)的父亲 = 删除节点的左孩子的最右孩子的左孩子，改值(2)
注意：删完以后，从父节点一直到递归到根节点检查是否失衡，并调整

B树

待补充

平衡多叉树-B树的查找

关键字数=子节点数-1！！！
根节点的子节点个数: [2, m]
而除根节点以外的非叶子节点的子节点个数：[⌈m/2⌉, m]
根节点的关键字个数：[1, m-1]
而除根节点以外的其它节点的关键字个数：[⌈m/2⌉-1， m-1]

非叶子节点的存储结构如下:
在这里插入图片描述

n个关键字，可表示<=A0，[A0,A1]，[A1,A2]…n+1个区间（n+1个指针）
时间复杂度:

        O 
       
      
        ( 
       
      
        l 
       
      
        o 
       
       
       
         g 
        
       
         m 
        
       
      
        n 
       
      
        ) 
       
      
     
       O(log_mn) 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.02778em;">O</span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.01968em;">l</span><span class="mord mathdefault">o</span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.03588em;">g</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.151392em;"><span class="" style="top: -2.55em; margin-left: -0.03588em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">m</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mord mathdefault">n</span><span class="mclose">)</span></span></span></span></span></li></ul> </li></ul>

红黑树

https://www.cnblogs.com/skywang12345/p/3245399.html#!comments
性质：

结点要么黑要么红
根结点黑
红结点的子结点是黑(3)
所有结点到达叶子结点的所有路径中，黑色结点个数一致(4)
最长路径不超过最短路径的两倍

插入：

叔叔结点为红：父亲结点黑(3)、祖父结点红(4)、叔叔结点黑(4)，进一步祖父结点
叔叔结点为黑(或空)，当前结点是右孩子：把父亲结点看作当前结点，把当前(父亲)结点进行左旋，进一步父亲结点
叔叔结点为黑(或空)，当前结点是左孩子：父亲结点黑(3)、祖父结点红(4)，把祖父结点进行右旋

删除：
略

优点：
红黑树放宽了平衡的条件，即二叉平衡树要求任意结点的左右子树高度相差不超过1；红黑树则通过四个性质来使得最长路径不大于最短路径的两倍，满足近似的平衡。
这样带来的好处主要有二：1. 虽然插入时，若不平衡，红黑树和二叉平衡树的调整都为O(1)；查找时两者都为O(logn)；但在删除时，若不平衡，二叉平衡树需要从不平衡结点递归往上调整，而红黑树最多3次调整； 2. 由于红黑树的平衡条件有所放宽，发生不平衡的次数也会降低。

哈希表

哈希表构造（常用的哈希函数）:
- 除留余数法：H(key) = key % p，其中p为不大于表长的质数、或者是不包含20以下质因子的合数
- 直接定址法：H(key) = a x key + b
- 数字分析法：通过对关键字的分析，选择产生冲突较少的关键字
- 平方取中法：对关键字取平方的中间几位
- 折叠法：将关键字分割成数位相同的几部分，取这几部分的叠加作为地址
哈希表查找（主要是找到处理冲突的方法）
- 开放地址法
  - 线性探测法
  - 二次探测法
  - 双哈希函数探测法:H_i = (H(key) + i * RH(key)) % m (i=1,2,3…m-1)
- 链地址法:冲突的链接在同一链表中
- 公共溢出法:定义一个公共的溢出表
- 再哈希法:预先定义一个哈希函数序列
  时间复杂度:
  定义装载因子为α = n/m，时间复杂度是α的函数，且受处理冲突方法的影响:

树、二叉树、森林

树

树的基本概念：
- 树的度：树内所有结点度的最大值为树的度
- 树的深度：树中所有结点层次的最大值为树的深度（一般根的层次为1）

树的性质：

树的结点个数 = 树的所有结点的度数和+1
树的结点个数 = 树的边个数+1

度为k的树的第i层，最多有

         k 
        
        
        
          i 
         
        
          − 
         
        
          1 
         
        
       
      
     
       k^{i-1} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.824664em; vertical-align: 0em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.03148em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span></span>个结点(1)</li><li>深度为h、度为k的树，最多有<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
    
     
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          0 
         
        
        
        
          h 
         
        
          − 
         
        
          1 
         
        
       
       
       
         k 
        
       
         i 
        
       
      
     
       \sum_{i=0}^{h-1}{k^i} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28872em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.989008em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">h</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord"><span class="mord mathdefault" style="margin-right: 0.03148em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span></span>个结点 (2)</li><li>具有n个结点的、度为k的树的最小深度：n = <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
    
     
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          0 
         
        
        
        
          h 
         
        
          − 
         
        
          1 
         
        
       
       
       
         k 
        
       
         i 
        
       
      
     
       \sum_{i=0}^{h-1}{k^i} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28872em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.989008em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">h</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord"><span class="mord mathdefault" style="margin-right: 0.03148em;">k</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span></span>，求得h(3)</li></ul> </li></ul>

二叉树

二叉树的基本概念
- 二叉树的度：树内所有结点度的最大值为二叉树的度（<=2）
- 深度=高度

二叉树的性质

第i层，最多有

          2 
         
         
         
           i 
          
         
           − 
          
         
           1 
          
         
        
       
      
        2^{i-1} 
       
      
    </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.824664em; vertical-align: 0em;"></span><span class="mord"><span class="mord">2</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span></span></span></span></span></span></span></span></span>个结点(1)</strong></li><li>深度为k的二叉树，最多有<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
    
     
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          0 
         
        
        
        
          k 
         
        
          − 
         
        
          1 
         
        
       
       
       
         2 
        
       
         i 
        
       
      
     
       \sum_{i=0}^{k-1}{2^i} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28872em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.989008em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.03148em;">k</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord"><span class="mord">2</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span></span>个结点(2)</li><li><strong>n0\n1\n2定理</strong>（n0 = n2 + 1）: 二叉树的结点个数 = n0 + n1 + n2；二叉树的边的个数 = n1 x 1 + n2 x 2，又：结点个数=边的个数+1，所以：…</li><li><strong>满二叉树</strong>：深度为k的二叉树，有<span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
    
     
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          0 
         
        
        
        
          k 
         
        
          − 
         
        
          1 
         
        
       
       
       
         2 
        
       
         i 
        
       
      
     
       \sum_{i=0}^{k-1}{2^i} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28872em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.989008em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.03148em;">k</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord"><span class="mord">2</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span></span>个结点</li><li><strong>完全二叉树</strong>：满二叉树顺序删去部分结点 
<ul><li>对于完全二叉树，从1开始从上往下、从左往右编号，第i个结点的2xi是左孩子、2xi+1是右孩子。i/2向下取整是父亲</li></ul> </li><li>具有n个结点的二叉树的最小深度：n = <span class="katex--inline"><span class="katex"><span class="katex-mathml"> 
    
     
      
       
       
         ∑ 
        
        
        
          i 
         
        
          = 
         
        
          0 
         
        
        
        
          h 
         
        
          − 
         
        
          1 
         
        
       
       
       
         2 
        
       
         i 
        
       
      
     
       \sum_{i=0}^{h-1}{2^i} 
      
     
   </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1.28872em; vertical-align: -0.29971em;"></span><span class="mop"><span class="mop op-symbol small-op" style="position: relative; top: -5e-06em;">∑</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.989008em;"><span class="" style="top: -2.40029em; margin-left: 0em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">i</span><span class="mrel mtight">=</span><span class="mord mtight">0</span></span></span></span><span class="" style="top: -3.2029em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight">h</span><span class="mbin mtight">−</span><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height: 0.29971em;"><span class=""></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.166667em;"></span><span class="mord"><span class="mord"><span class="mord">2</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.824664em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">i</span></span></span></span></span></span></span></span></span></span></span></span></span>，求得h(3)</li></ul> </li><li>二叉树的遍历

层次遍历
先、中、后序遍历
后序+中序构造二叉树：看后序的最后一个元素确定根结点，再去中序中确定该根节点的左右子树，然后递归
先序+中序构造二叉树：看先序的第一个元素确定根结点，再去中序中确定该根节点的左右子树，然后递归

二叉树与表达式:
- 将中缀表达式转换成后缀表达式（栈中存运算符）：如果是运算符，判断和栈顶运算符的优先级，如果栈顶元素是"(“或者优先级更小，则当前运算符入栈，否则栈顶元素出栈加入到列表中，继续出栈新的元素判断；如果是”("，直接入栈；如果是")"，循环出栈，加入到列表，直到遇到"("；如果是数字，直接入列表。最后把栈中的剩余元素依次出栈加入到列表。
- 由后缀表达式构建一棵二叉树：如果是数字，创建单结点入栈；如果是运算符，创建单节点，并依次出栈元素2和元素1结点，设置运算符结点的左子树为元素1，右子树为元素2，然后将该结点入栈
- ？？？后缀表达式可以直接计算了。数字入栈，遇到运算符，依次出栈元素2和元素1，计算元素1 运算符元素2，并把结果入栈
- 先序遍历二叉树得到前缀表达式：这没什么好说
- 借助栈对前缀表达式求值（栈中存数字）：前缀表达式如“-×+3456”，所以从后往前遍历，如果是数字，则入栈；如果是运算符，则依次出栈元素1和元素2，计算结果继续入栈
线索二叉树
- 缘由：以链表形式存储的n个结点的二叉树中，一个有2n个指针，其中n+1个指针是没有被用到的。线索二叉树解决上述问题的同时，记录了结点的前驱后继的关系。（n+1的证明：n个节点，一共有2n个指针。其中空指针个数=2n_0+n_1，计算得。）
- 数据结构:[lchild, ltag, data, rtag, rchild]，如果一个结点左子树为空，则指向先驱结点；如果一个结点右子树为空，则指向后继结点。
哈夫曼树
- 概念：
 - 树的PL：所有结点到达根节点的路径长之和
 - 树的IPL：所有内部结点…
 - 树的EPL：所有外部结点…
 - 哈夫曼树：对于含有n个叶子结点的二叉树，假定它们各自有权重，哈夫曼树是带权路径之和最小的二叉树。哈夫曼树不存在度为1的结点。
- 应用：对于给定的一串字符串（报文），用最少的二进制代码对其进行编码，完成数据压缩。具体来讲，统计字符串中各个字符出现的次数，作为权值，构造哈夫曼树，使得权值大的字符结点距离根节点远，小的字符结点距离根节点近。另外，对字符的编码满足：任何一个字符的编码不是其它字符编码的前缀。
- 构造方法：把n个叶子结点看作n棵树。每一次循环，选择树中权重最小的两棵，构造一个新的二叉树，根的权重为两个子树根节点的权重之和。删除原来的两棵，加入新构造的二叉树。
- 应用：编码。给出现频率高（权重大）的字符以更短的PL，定义树的左分支代表编码’0’，右分支代表编码’1’。哈夫曼树用于编码是一种平均长度最短的前缀编码（任何符号的编码不是其它符号编码的前缀）。
图

图的相关术语
- 网:带权图
- 完全图：
 - 无向完全图:n个结点，n-1 + n-2 + … + 1 = n(n-1) / 2条边
 - 有向完全图:n个结点，n(n-1)条边
- 度：边数=图的度之和/2
- 路径:
 - 简单(初等)路径:路径对应的顶点序列中顶点不重复
 - 路径长度:边的个数(图)、边的权重之和(网)
 - 回路:路径的第一个顶点和最后一个顶点相同
 - 简单回路:同上，且没有重复顶点
- 连通：
 - 连通图:无向图，任意两个点连通
 - 连通分量:极大的连通子图，这里的极大是指点的个数尽可能多
 （给定一个图，如果是连通图，则它的连通分量就是它本身，否则…）
 - 强连通图:有向图，任意两条点存在路径
 - 强连通分量:极大的强连通子图
- 生成树与最小生成树:
 - 生成树:无权的连通图中，极小的连通子图，这里的极小是指边的个数尽可能少（n个结点-》n-1条边）
 - 最小生成树:有权的连通图中，极小的连通子图，n-1条边，且权重之和最小
 - 性质:有n个顶点、n-1条边，多一条->有环，少一条->不连通
图的表示方法:
- 数组:创建时间复杂度:O(n2(邻接矩阵)+e(遍历所有的输入边)n(根据输入顶点，在列表中索引，找到对应下标)) ；空间复杂度n2
- 邻接:邻接链表。创建时间复杂度:O(n+e)；空间复杂度n+e
图的遍历:
- 深
- 广
- 时间复杂度:邻接矩阵:O(n2(每一个结点遍历自己的邻接结点))、邻接链表:(O(n(初始化访问标志)+e(遍历所有的边)))
图的最小生成树:
- prim算法（点，适用于稠密图）：顶点集分为已经访问集和未访问集合。首先把开始顶点加入到已经访问集，每次循环，选择从已经访问集到达未访问集合的最小的边v1->v2。把v2加入到已经访问集，并更新。时间复杂度为O(n2)
- kruskal算法（边，适用于稀疏图）：给所有边排序。每次加入一条权重最小而且两个端点没有直接或间接相连的边。时间复杂度O(ElogE(排序))
图的最短路径:
- dijkstra算法（单源点）：顶点集分为已经访问集和为访问集。首先把开始顶点加入到已访问集，每次循环，选择从开始结点到达未访问集的最小的边start->v2。把v2加入到已经访问集，并更新开始结点与剩下为访问集各个顶点的最短距离。时间复杂度为O(n2)
- floyd算法（多源点）：每次选定一个顶点作为中间结点，遍历其它所有顶点对，更新之间的距离。时间复杂度为O(n3)
图的拓扑排序(AOV(activity on Vertex Network) | DAG(directed acyclic graph)):
- 广度优先搜索：初始化一个队列，把入度为0的结点放入。每一次pop一个顶点，加入拓扑序列。并删除它所有的出边，判断出边对应的另一个结点的度是否变为0，如变为0，则也入队列。时间复杂度为O(n(队列会pop n次)+E(删除了图中所有的边))
- 深度优先搜索：当一个结点没有出边，或者出边所对应的结点已经访问完了（已经加入到栈中），这个结点入栈。时间复杂度也是O(n+E)
常见问题

时间复杂度

函数增长符号

https://blog.csdn.net/hugebawu/article/details/86303539
- Ɵ：渐进紧确界（存在c1、c2，n0，当n>=n0时，满足0<c1g(n)<=f(n)<=c2g(n)，则f(n)=Ɵ(g(n)) )
- O：渐进上界（存在c1、n0，当n>=n0时，满足f(n)<=c1g(n)，则f(n) = O(g(n)) )
- Ω：渐进下界（存在c1、n0，当n>=n0时，满足f(n)>=c1g(n)，则f(n) = Ω(g(n)) ）
- o：非渐进紧确上界（任意正数c，存在n0，当n>=n0时，满足f(n)<c(g(n)) ）
- ω：非渐进紧确下界（任意正数c，存在n0，当n>=n0时，满足f(n)>c(g(n)) ）
常见时间复杂度

常对幂指阶
```
 O 
 
 
 ( 
 
 
 1 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 l 
 
 
 g 
 
 
 n 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 n 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 l 
 
 
 g 
 
 
 n 
 
 
 x 
 
 
 n 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 n 
 
 
 2 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 
 2 
 
 
 n 
 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 n 
 
 
 ! 
 
 
 ) 
 
 
 &lt; 
 
 
 O 
 
 
 ( 
 
 
 
 n 
 
 
 n 
 
 
 
 ) 
 
 
 
 O(1)&lt;O(lgn)&lt;O(n)&lt;O(lgnxn)&lt;O(n2)&lt;O(2^n)&lt;O(n!)&lt;O(n^n) 
 
 
 O(1)&lt;O(lgn)&lt;O(n)&lt;O(lgnxn)&lt;O(n2)&lt;O(2n)&lt;O(n!)&lt;O(nn) 
```
P&NP&NPC&NP-HARD

参考：什么是P问题、NP问题和NPC问题
P问题：能够在多项式的时间内找到解的问题
NP问题：不能确定是否能在多项式的时间内找到解，但是能在多项式内验证一个问题的解或者说在多项式时间内猜出一个问题的解，的问题。比如汉密尔顿回路问题（是否存在一条回路，恰好经过所有结点一次）：1. 运气足够好，猜一条路，只需要去观察这条路是否满足条件–>NP问题；2. 把问题改成给定一个图，是否不存在汉密尔顿回路，此时必须比较所有的路，才能得到答案–>不是NP问题。
NPC问题：1. 首先是一个NP问题 2. 所有的NP问题都可以约化到它（什么是约化？–>问题A转换到问题B，如果问题B解出，问题A就能解出），它是一个最为复杂的NP问题。如：逻辑电路问题。另：如何证明一个问题是NPC问题–>首先证明它是一个NP问题，然后证明一个已知的NPC问题能够约化到它（传递性）
NP-HARD问题：1. 所有NP问题都可以约化到它 2. 但它本身不一定是NP问题。

动态规划

https://www.cnblogs.com/aabbcc/p/6504597.html#q5

原理：

分治法得到的子问题相互独立，动态规划的子问题有重叠部分。
两种解法：1. 递归自顶向下算法（记忆化搜索） 2. 自底向上

应用：

硬币找零

给定：coins = [面值1，面值2，…面值n]，硬币数量不限，total = 待凑齐的零钱个数
求解：凑齐total，需要用到的最少硬币数目
转移方程：min_coin[i] = min(min_coin[i - coins[0]], min_coin[i - coins[1]], … min_coin[i - coins[n]]) + 1

单路取苹果

装配线调度

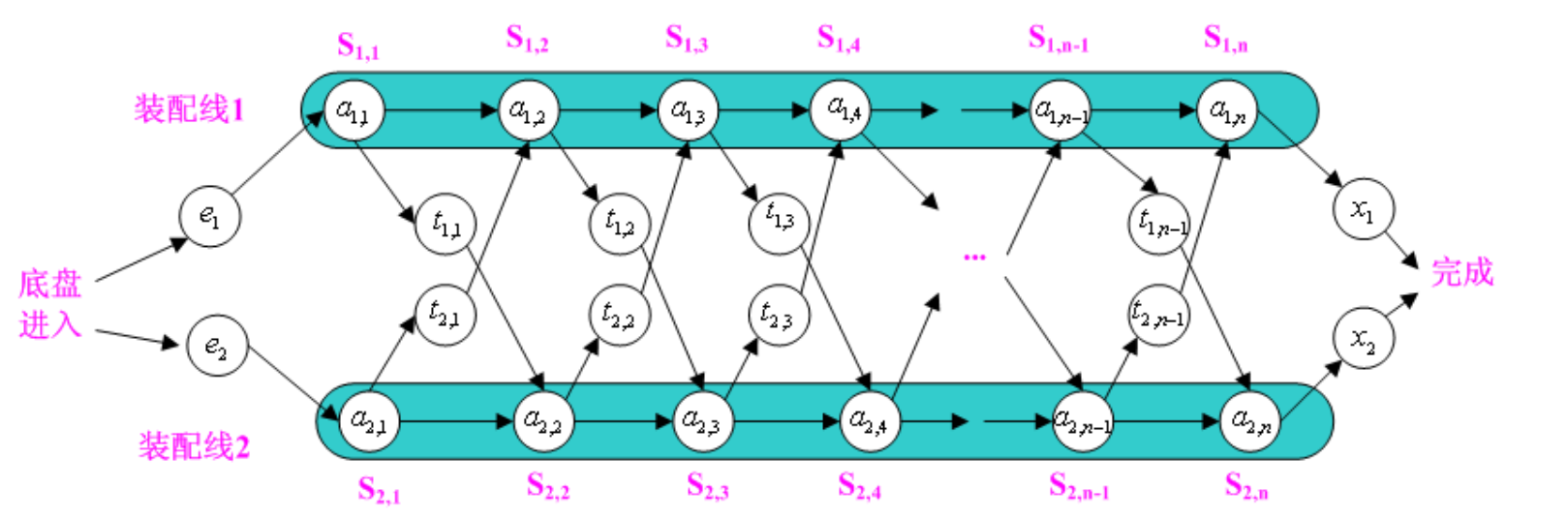
字符串相似度/编辑距离

看不懂

最长公共子序列

https://blog.csdn.net/hrn1216/article/details/51534607
给定：序列1 = {字符1，字符2，…字符m}，序列2 = {字符1，字符2，…字符n}
求解：序列1和序列2公共子序列的最大长度
转移方程：

最长递增子序列

https://blog.csdn.net/u012505432/article/details/52228945
给定：序列 = {字符1，字符2，…字符n}
求解：序列的最长递增子序列
求解思路：
- O(n)：dp[i]表示以第i个字符为末尾的递增子序列的最大长度（初始化为1）
 dp[i] = max(dp[k]) + 1，其中，序列[k] < 序列[i]
- O(nlogn)：dp[i]表示长度为i的递增子序列的末尾字符
 从左到右遍历序列，如果序列[j]大于dp[i]，则dp[i+1] = 序列[j]；否则通过二分查找，找到dp[k-1] < 序列[j] < dp[k]，并把dp[k] = 序列[j]
最大连续子序列和

给定：序列 = {数字1，数字2，…数字n}
求解：连续子序列的最大和
转移方程： dp[i] = max(序列[i], 序列[i] + dp[i-1])

最大连续子序列积

给定：序列 = {数字1，数字2，…数字n}
求解：连续子序列的最大积
求解思路：
max_[k] = max(max_[k-1] x 序列[k], min_[k-1] x 序列[k], 序列[k])
min_[k] = min(max_[k-1] x 序列[k], min_[k-1] x 序列[k], 序列[k])
ans = max(max_)
这里的min_是因为：负负得正，能够翻盘

最长公共子串

tbc

矩阵连乘

给定：矩阵序列 = {p_0xp_1, p_1xp_2, p2xp3, … }
求解：矩阵乘法所需要的最少计算次数
求解思路：
对于i…j的矩阵子序列，遍历划分点k，dp[i][j] = min[dp[i][k] + dp[k+1][j] + (p_i-1)(p_k)(p_j)]

分治

原理：
和动态规划一样，分治问题也具有最优子结构，即可以把原问题分解为若干个较小规模的子问题。这些子问题是相互独立的，如果得到求解，则可以通过合并，来解决原问题。

应用：
- 二分查找
- 汉诺塔问题：把原问题分解为：1. 最大圆盘以上的圆盘从A借助B移动到C；2. 把最大圆盘从A移动到B； 3. 把最大圆盘以上的圆盘从C借助A移动到B。
- 快速排序：每次选择一个基准元素，把小于该元素的元素移动到左侧，大于该元素的元素移动到右侧。递归求解左右子序列。基准元素的选择方法：1. 固定选择序列头\尾的元素； 2. 随机选择； 3. 三数取中选择（头、尾、中）（其中的思想，选择的基准元素大小刚好能够把当前序列等分，则性能最好）
- 归并排序
贪心

原理：
贪心问题具有最优子结构，且要保证每一个子问题的局部最优解能够导致原问题的最优解

应用：
- 最小生成树：prim、kruskal
- 最短路径：dijisktra
并查集

原理：用于元素分组的问题，维护两个操作：合并（将不属于同一组的元素合并为同一组，具体为将某一个元素的祖先节点更改为另一个元素的祖先节点）；查询（判断两个元素是否属于同一组）。并查集使用一个元素来作为一个组的祖先。另外，为解决所形成的树深度太大的问题，可以在查询时动态修改元素的父亲就是他的祖先。

回溯剪枝

原理：深度优先搜索，每一步按一定条件进行选择，直到达到最终的目标。如果到达某一步时，发现无法到达最终目标，则退回到之前步，尝试新的选择。
应用：
- n皇后：按行搜索。每一行遍历n个可能的列，如果某一列上，满足1. 没有列重复 2. 没有斜对角重复，则放，开始下一行的搜索。时间复杂度：O(n!)
KMP算法

https://www.zhihu.com/question/21923021
字符串匹配算法，利用next数组存储公共前后缀，来扩大匹配失败后的移动步长。
利用字符串匹配、动态规划的思想，优化创建next数组的过程。
最终达到O(m(主串长度)+n(模式串长度))的时间复杂度。