图论-第二章 图

前言

主要写的目的是方便期末复习图论（张清华等老师）的各个章节，不适于零基础。

一、图的基本概念

1.图的定义及相关概念

1.无序对

无序对：任意两个元素构成为（a，b）的形式

无序积：两个集合的无序对组成的集合

2.无向图

用集合G表示=<V,E>,即<结点，边>的集合

3.有向图

D=<V,E>

4.标定图

图的结点和边都标记名称的标定图

5.点和边的关系

一条边关联的两个结点重合（即为同一个结点）称为环或回路

无边关联的结点称为孤立点

6.图的阶数

平凡图：只有一个结点，且无边

7.边的重数

关联于同一个结点的多条边称为平行边（有向图需要方向一致）

不含平行边的和环称为简单图

2.结点的度

1.度数

与结点相关联的边数即为度数，用deg（v）表示度数(奇度、偶度、最大度、最小度)

2.出度+、入度-

 环既是出，又是入，无向图度+2，有向图出度+1，入度+1

3.悬挂

度为1的点为悬挂点 、其关联的边为悬挂边

4.度序列

按照点V（v1...）序列，构造的度序列（deg（v1）...）

5.握手定理

-------------------------------12.21

(1)边数为m，则图共2m度segema deg（vi）=2m

(2)有向图的segema deg+=segema deg-=2m

(3)奇度结点的个数必为偶数

两个例子：

握手定理的应用例子（握手定理第三条）：

 3.完全图、正则图、补图、子图

完全图Kn：任意两结点都有边相连，边数为n*(n-1)/2

有向完全图Dn：任意两结点都有一对方向相反的边相连边数为n*(n-1)

竞赛图：有向简单图任意两结点都有一条边相连，边数为n*(n-1)/2

正则图：在无向简单图，每个结点的度数为k，该图称为k-正则图（完全图为n-1-正则图）

补图：两个图的边集能组成完全图，则称这两个图互为补图

子图：边和顶点都属于

生成子图：顶点相同，边属于

导出子图：

结点属于，子图结点的所有边都存在在子图中（点导出子图），简称导出子图

结点属于，子图边的所有结点都存在在子图中（边导出子图）G[E']

4.图的同构

同构的必要条件：

（1）结点相同

（2）边数相同

（3）对应点的度数相同

例子：

例子：

但是结点相等，边数相等，度序列相同的两个图依旧可能不同构

5.图的运算

删除边G-E'、点G-V‘

收缩边G\e

加新边

G+（v2，v5）或者

---------------------------------------------------------12.22

二、图的连通性

1.通路

1. 通路 回路

通路中的结点和边可能重复（存在环）

简单通路：e1...en互不相同，无重复边（存在环）

路径：通路中的v1...vn互不相同，无重复点

回路：起点和终点相等

简单回路：e1...en互不相同

圈：回路中的v1...vn互不相同（长度为奇数的圈为奇圈，偶为偶圈）

2.图的连通性

1.结点的连通

一个无向图中的任意两个结点都是连通的，则称图G是连通图（平凡图就是连通图）

2.连通分支

分支数用w（G）表示

3.可达结点

4.结点间的距离

5.有向连通图

 定理：

有向连通图是强连通图当且仅当D存在一条经过每个结点至少一次的回路

3.无向图的连通性

1.点割集 割点

从连通图中删去一个点割集（删除点以及其点关联的边）得到的子图是不连通的（增加连通分支）

两个条件：

{v2,v3,v4}不是，因为它的子集{v2,v4}删去后，和原始图的连通分支=1不一样

2.点连通度

 从连通图中删去一个点割集后得到的子图是不连通的

连通度是为了产生一个不连通图所要删除结点的最少数目

规定平凡图的连通度是0，规定完全图Kn的连通度是n-1

非连通图的连通度为0

存在割点的连通图的连通度为1

k-连通图中任意删除k-1个结点后仍然连通

3.边割集 割边（桥）

从连通图中删去一个边割集得到的子图是不连通的

两个条件：

4.边连通度

5.连通度（有可能）

 6.割点和割边的判断（不重要）

定理：

定理：

定理：

7.扩大路径法（不重要）

定理：

4.二部图（有涉及）

1.二部图的定义

n阶零图为二部图

2.二部图的判定（有可能）

三、图的矩阵表示

1.关联矩阵

1.无向关联矩阵

结点和边的关系的矩阵（mij是结点与边关联的次数）

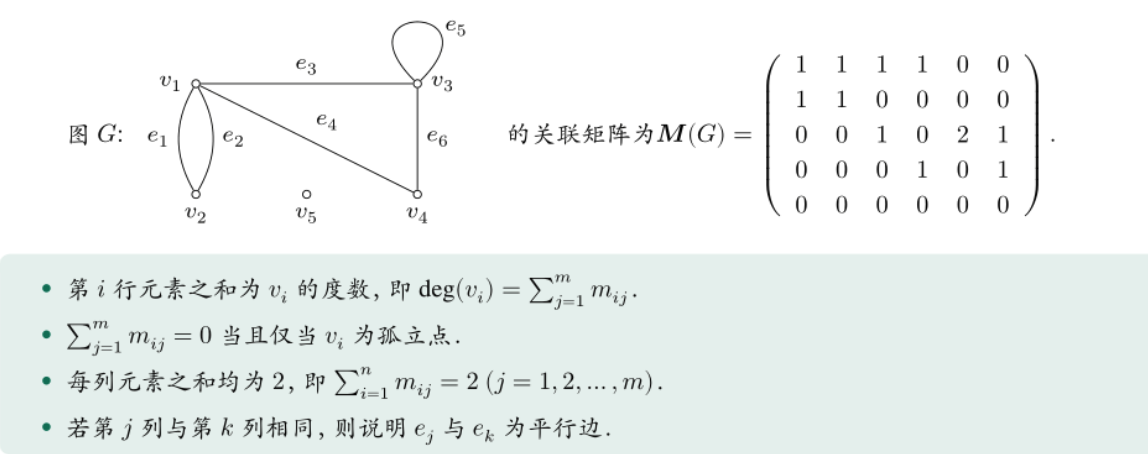
2.无环有向图关联矩阵

入度是-1

2.邻接矩阵

有向邻接矩阵

例子

行之和为出度，列之和为入度

2.无向简单图邻接矩阵

例子

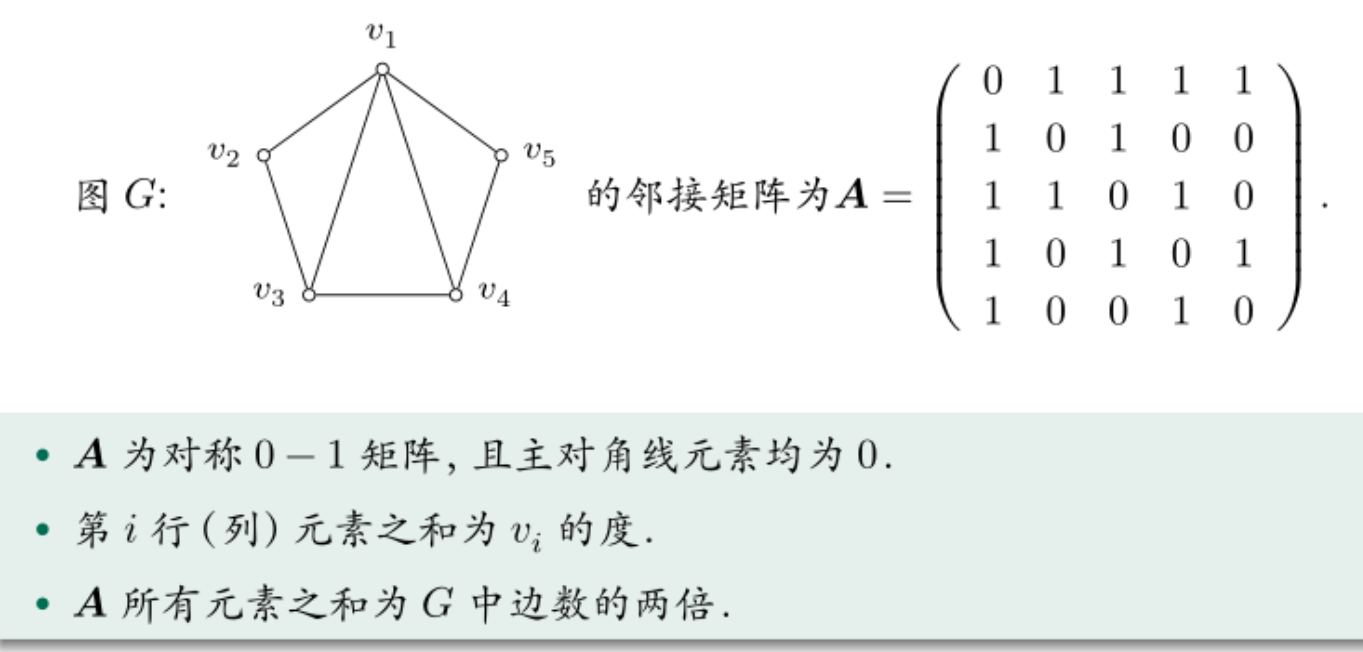
定理：

例子：

3.可达矩阵

例子

4.可达矩阵的计算

1.利用邻接矩阵A和单位矩阵E

B=E+A+A**2+...+A**(n-1)

可达矩阵P=B（Bij=0=0,Bij>0=1）

2.布尔运算

计算可达矩阵，只关心两结点是否存在通路。不用关心通过的长度以及数目

布尔积（矩阵的乘法）：A*A=A交A，

布尔和：A+A=A并A

此时可达矩阵的计算为

3.Warshall算法计算可达矩阵

如果是四阶矩阵进行warshall算法，

将第一行与其他第一列为1的行进行或运算得到A1，然后将得到的结果的第二行与其他第二列不为1的行进行或运算得到A2...最后得到A4，最后与单位矩阵E进行布尔和

-------------------------------------------------------12.24

四、欧拉图与哈密尔顿图

1.欧拉图

1.欧拉图的定义

欧拉图：经过图G每一条边一次且仅一次的回路，称为欧拉回路，图叫做欧拉图

半欧拉图：经过图G每一条边一次且仅一次的路，图称为半欧拉图

2.欧拉图的判定

欧拉图的必要条件（能推）：无向连通图G（欧拉图）中无奇度结点

半欧拉图的必要条件：当且仅当G中有且仅有两个奇度结点

例子：

3.半欧拉图的判定（省略）

4.有向欧拉图

2.哈密尔顿图

1.哈密尔顿图的定义

哈密尔顿图：经过图G每一个结点一次且仅一次的回路，称为哈密尔顿回路，图叫做哈密尔顿图

半哈密尔顿图：经过图G每一个结点一次且仅一次的路，图称为半哈密尔顿图

2.哈密尔顿图的判定

哈密尔顿图必要条件（不重要）

w是连通分支数

例子：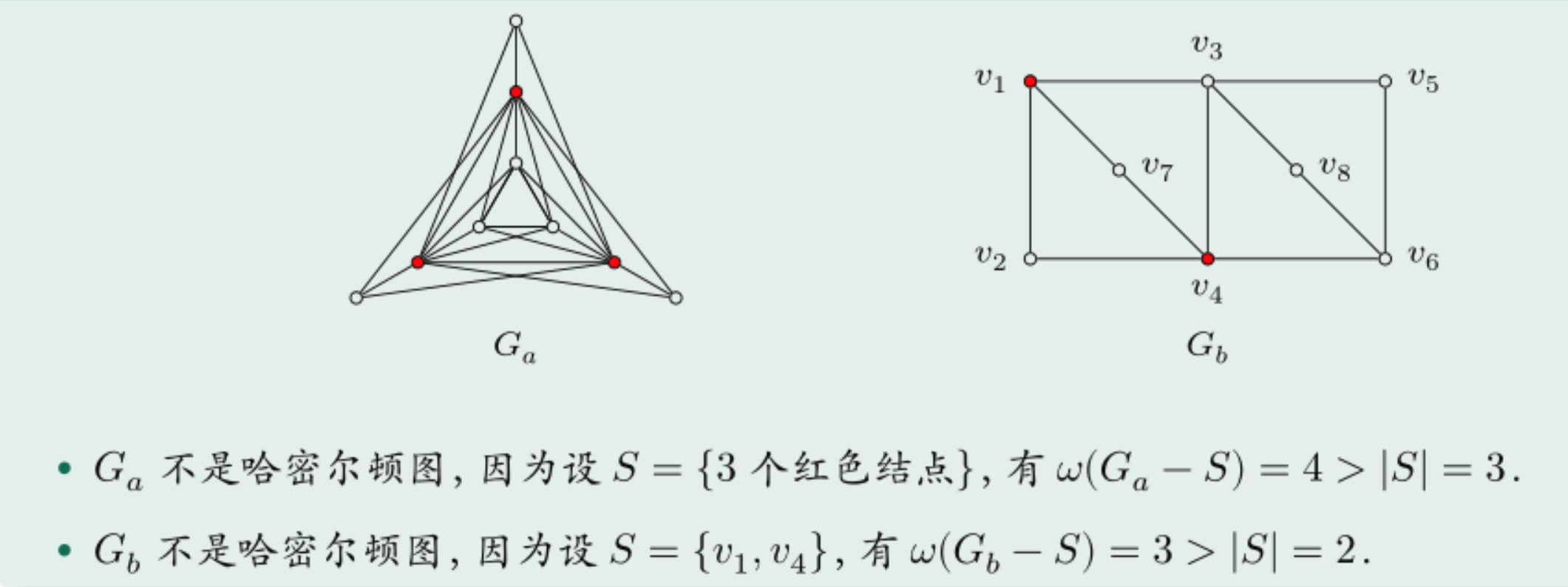

哈密尔顿图充分条件（重点）

例子：

含哈密尔顿路的充分条件（略）

半哈密尔顿图必要条件

3.旅行商问题