Network Applications of Bloom Filters: A Survey
一、False Positive rate 假阳性 / 误判率
Bloom Filter有一个可预测的误判率,可通过调整hash function数量k,以及位数组m大小来控制。
参数:
m:bloom filter size
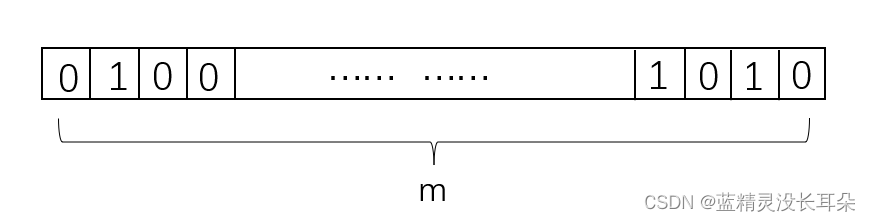
n:elements number
k:hash函数个数 / hash次数
assume:kn < m / m >> n(保证filter不满)
1. self
一个element,hash一次,某位置1的概率:
P
(
1
个
e
l
e
m
e
n
t
,
h
a
s
h
一次,某位置
1
)
=
1
m
P(1个element,hash一次,某位置1) = \frac {1} {m}
P(1个element,hash一次,某位置1)=m1
一个element,hash一次,该位不置1的概率:
P
(
1
个
e
l
e
m
e
n
t
,
h
a
s
h
一次,该位不置
1
)
=
1
−
1
m
P(1个element,hash一次,该位不置1) = 1 - \frac 1 m
P(1个element,hash一次,该位不置1)=1−m1
一个element,hash k次,该位不置1的概率:
P
(
1
个
e
l
e
m
e
n
t
,
h
a
s
h
k
次,该位不置
1
)
=
(
1
−
1
m
)
k
=
(
(
1
−
1
m
)
−
m
)
−
k
m
≈
e
−
k
m
\begin{aligned} P(1个element,hash \ k次,该位不置1) &= (1 - \frac 1 m)^k \\ &= ((1 - \frac 1 m)^{-m}) ^{- \frac k m}\\ &≈ e^{-\frac k m} \end{aligned}
P(1个element,hash k次,该位不置1)=(1−m1)k=((1−m1)−m)−mk≈e−mk
上式用e的极限:
lim
x
→
∞
(
1
+
1
x
)
x
=
e
lim
x
→
∞
(
1
−
1
x
)
x
=
lim
x
→
∞
(
(
1
+
(
−
1
x
)
)
−
x
)
−
1
=
e
−
1
\begin{aligned} \lim_{x\to \infty} (1 + \frac 1 x) ^x &= e\\ \lim_{x\to \infty} (1 - \frac 1 x) ^x &= \lim_{x\to \infty} ((1 + (- \frac 1 x)) ^{-x})^{-1} \\ &= e^{-1} \end{aligned}
x→∞lim(1+x1)xx→∞lim(1−x1)x=e=x→∞lim((1+(−x1))−x)−1=e−1
n个elements,hash k次,某位不置1的概率:
P
(
n
个
e
l
e
m
e
n
t
s
,
h
a
s
h
k
次,某位不置
1
)
=
(
1
−
1
m
)
k
n
≈
e
−
n
k
m
\begin{aligned} P(n个elements,hash \ k次,某位不置1)&=(1 - \frac 1 m)^{kn}\\ &≈ e^{-\frac {nk} m} \end{aligned}
P(n个elements,hash k次,某位不置1)=(1−m1)kn≈e−mnk
n个elements,hash k次,某位置1的概率:
这个概率是:n个elements,hash k次之后的状态中,bloom filter中1的概率。
P
(
n
个
e
l
e
m
e
n
t
s
,
h
a
s
h
k
次,某位置
1
)
=
1
−
(
1
−
1
m
)
k
n
≈
1
−
e
−
k
n
m
\begin{aligned} P(n个elements,hash \ k次,某位置1)&=1 - (1 - \frac 1 m)^{kn}\\ &≈ 1 - e^{-\frac {kn} m} \end{aligned}
P(n个elements,hash k次,某位置1)=1−(1−m1)kn≈1−e−mkn
PS:
以上,“置1” -> “不置1” -> “置1”,这样计算原因:hash k次,有重复置1。
假阳 / 误判:新的element来,hash k次之后,原本不应全为1,但事实是,得到的全是1。
(新来的需要hash k次)
P
(
f
a
l
s
e
p
o
s
i
t
i
v
e
)
=
(
1
−
(
1
−
1
m
)
k
n
)
k
≈
(
1
−
e
−
k
n
m
)
k
\begin{aligned} P(false \ positive) &=(1 - (1 - \frac 1 m)^{kn})^k\\ &≈ (1 - e^{-\frac {kn} m})^k \end{aligned}
P(false positive)=(1−(1−m1)kn)k≈(1−e−mkn)k
以上误判率中,m↑ p↓ / n↓ p↓,确定p随k的变化。
先定m,根据内存大小确定,给定一个合适的m值。
令
f
(
k
)
=
(
1
−
e
−
k
n
m
)
k
两边取
l
n
l
n
(
f
(
k
)
)
=
l
n
(
(
1
−
e
−
k
n
m
)
k
)
=
k
l
n
(
1
−
e
−
k
n
m
)
两边求导
1
f
(
k
)
f
′
(
k
)
=
l
n
(
1
−
e
−
k
n
m
)
+
k
(
l
n
(
1
−
e
−
k
n
m
)
)
′
=
l
n
(
1
−
e
−
k
n
m
)
+
k
(
1
1
−
e
−
k
n
m
)
(
1
−
e
−
k
n
m
)
′
=
l
n
(
1
−
e
−
k
n
m
)
+
k
(
1
1
−
e
−
k
n
m
)
(
−
e
−
k
n
m
)
(
−
k
n
m
)
′
=
l
n
(
1
−
e
−
k
n
m
)
+
k
(
1
1
−
e
−
k
n
m
)
(
−
e
−
k
n
m
)
(
−
n
m
)
=
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
1
−
e
−
k
n
m
导数
f
′
(
k
)
=
0
时,求一个极值:
1
f
(
k
)
f
′
(
k
)
=
1
f
(
k
)
⋅
0
=
0
=
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
1
−
e
−
k
n
m
去分母:
0
=
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
0
=
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
−
e
−
k
n
m
(
−
k
n
m
)
0
=
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
−
e
−
k
n
m
l
n
e
−
k
n
m
即:
e
−
k
n
m
l
n
e
−
k
n
m
=
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
\begin{aligned} 令 \qquad f(k) &= (1 - e^{-\frac {kn} m})^k \\ 两边取ln \quad ln(f(k)) &= ln((1 - e^{-\frac {kn} m})^k) \\ &= kln(1 - e^{-\frac {kn} m}) \\ 两边求导 \qquad \frac 1 {f(k)}f'(k) &= ln(1 - e^{-\frac {kn} m}) + k(ln(1 - e^{-\frac {kn} m}))' \\ &= ln(1 - e^{-\frac {kn} m}) + k(\frac 1 {1 - e^{-\frac {kn} m}})(1 - e^{-\frac {kn} m})' \\ &= ln(1 - e^{-\frac {kn} m}) + k(\frac 1 {1 - e^{-\frac {kn} m}})(- e^{-\frac {kn} m})(-\frac {kn} m)' \\ &= ln(1 - e^{-\frac {kn} m}) + k(\frac 1 {1 - e^{-\frac {kn} m}})(- e^{-\frac {kn} m})(-\frac n m) \\ &= ln(1 - e^{-\frac {kn} m}) + \frac {\frac {kn} m e^{-\frac {kn} m}} {1 - e^{-\frac {kn} m}}\\ 导数f'(k) = 0 时,求一个极值: \\ \frac 1 {f(k)}f'(k)&= \frac 1 {f(k)} · 0 \\ &= 0 \\ &= ln(1 - e^{-\frac {kn} m}) + \frac {\frac {kn} m e^{-\frac {kn} m}} {1 - e^{-\frac {kn} m}}\\ 去分母:0 &= (1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) + \frac {kn} m e^{-\frac {kn} m} \\ 0 &= (1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) - e^{-\frac {kn} m}(-\frac {kn} m) \\ 0 &= (1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) - e^{-\frac {kn} m}lne^{-\frac {kn} m} \\ 即:e^{-\frac {kn} m}lne^{-\frac {kn} m}&= (1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) \\ \end{aligned}
令f(k)两边取lnln(f(k))两边求导f(k)1f′(k)导数f′(k)=0时,求一个极值:f(k)1f′(k)去分母:000即:e−mknlne−mkn=(1−e−mkn)k=ln((1−e−mkn)k)=kln(1−e−mkn)=ln(1−e−mkn)+k(ln(1−e−mkn))′=ln(1−e−mkn)+k(1−e−mkn1)(1−e−mkn)′=ln(1−e−mkn)+k(1−e−mkn1)(−e−mkn)(−mkn)′=ln(1−e−mkn)+k(1−e−mkn1)(−e−mkn)(−mn)=ln(1−e−mkn)+1−e−mknmkne−mkn=f(k)1⋅0=0=ln(1−e−mkn)+1−e−mknmkne−mkn=(1−e−mkn)ln(1−e−mkn)+mkne−mkn=(1−e−mkn)ln(1−e−mkn)−e−mkn(−mkn)=(1−e−mkn)ln(1−e−mkn)−e−mknlne−mkn=(1−e−mkn)ln(1−e−mkn)
令:
{
x
=
e
−
k
n
m
y
=
1
−
e
−
k
n
m
,
x
+
y
=
1
上式可写为:
x
l
n
x
=
y
l
n
y
讨论
f
(
x
)
=
x
l
n
x
函数:
f
′
(
x
)
=
l
n
x
+
1
f
′
(
x
)
=
0
时,解得
x
=
1
e
f
(
1
e
)
=
−
1
e
,
f
(
0
)
=
0
,
f
(
1
)
=
0
\begin{aligned}&令: \begin {cases} x = e^{-\frac {kn} m} \\ y = 1 - e^{-\frac {kn} m} \end{cases},x + y = 1 \\ &上式可写为:xlnx = ylny \\ &讨论f(x) = xlnx 函数 :f'(x) = lnx + 1 \\ &f'(x) = 0时,解得x = \frac 1 e \\ &f(\frac 1 e) = -\frac 1 e,f(0) =0,f(1) = 0\end{aligned}
令:{x=e−mkny=1−e−mkn,x+y=1上式可写为:xlnx=ylny讨论f(x)=xlnx函数:f′(x)=lnx+1f′(x)=0时,解得x=e1f(e1)=−e1,f(0)=0,f(1)=0
绘制函数图像如图:
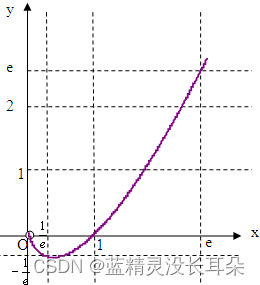
要求:
{
x
+
y
=
1
x
l
n
x
=
y
l
n
y
函数值相等
,唯一解:
x
=
y
=
1
2
\begin{aligned} 要求:\begin {cases} \begin{equation} x + y = 1\qquad\end{equation} \\ \begin{equation} xlnx = ylny \ 函数值相等\quad \end{equation} \end{cases},唯一解:x=y=\frac 1 2 \\ \end{aligned}
要求:{x+y=1xlnx=ylny 函数值相等,唯一解:x=y=21
解释:
因为函数值相等的解,只能在[0, 1]区间,
但是该区间内的解不满足(1)式,因为函数不对称。
具体如下图所示:
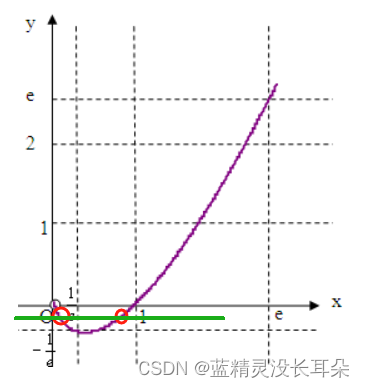
由以上可知,
x
=
y
=
1
2
即:
x
=
e
−
k
n
m
=
1
2
−
k
n
m
=
l
n
1
2
=
l
n
2
−
1
=
−
l
n
2
k
=
m
n
l
n
2
即:
f
′
(
k
)
=
0
时,
k
=
m
n
l
n
2
导数等于
0
的点,
说明
k
=
m
n
l
n
2
这是个极值点,需要讨论两侧单调性
\begin{aligned} 由以上可知,&x = y = \frac 1 2 \\ 即:&x = e^{-\frac {kn} m} = \frac 1 2 \\ -\frac {kn} m &=ln\frac 1 2 \\ &= ln2^{-1} \\ &= -ln2 \\ k &= \frac m nln2 \\ 即:&f'(k) = 0 时,k = \frac m nln2\\ 导数等于0的点,&说明k = \frac m nln2这是个极值点,需要讨论两侧单调性 \end{aligned}
由以上可知,即:−mknk即:导数等于0的点,x=y=21x=e−mkn=21=ln21=ln2−1=−ln2=nmln2f′(k)=0时,k=nmln2说明k=nmln2这是个极值点,需要讨论两侧单调性
f
(
k
)
=
(
1
−
e
−
k
n
m
)
k
f
′
(
k
)
=
0
时,
k
=
m
n
l
n
2
1
f
(
k
)
f
′
(
k
)
=
l
n
(
1
−
e
−
k
n
m
)
+
k
(
l
n
(
1
−
e
−
k
n
m
)
)
′
f
′
(
k
)
=
f
(
k
)
[
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
1
−
e
−
k
n
m
]
=
(
1
−
e
−
k
n
m
)
k
[
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
1
−
e
−
k
n
m
]
=
(
1
−
e
−
k
n
m
)
k
−
1
[
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
+
k
n
m
e
−
k
n
m
]
=
(
1
−
e
−
k
n
m
)
k
−
1
[
(
1
−
e
−
k
n
m
)
l
n
(
1
−
e
−
k
n
m
)
−
e
−
k
n
m
l
n
e
−
k
n
m
]
可以写成
=
(
1
−
e
−
k
n
m
)
k
−
1
(
y
l
n
y
−
x
l
n
x
)
的形式
\begin{aligned} f(k) &= (1 - e^{-\frac {kn} m})^k\\ f'(k) &= 0 时,k = \frac m nln2\\ \frac 1 {f(k)}f'(k) &= ln(1 - e^{-\frac {kn} m}) + k(ln(1 - e^{-\frac {kn} m}))' \\ f'(k) &= f(k)[ln(1 - e^{-\frac {kn} m}) +\frac {\frac {kn} m e^{-\frac {kn} m}} {1 - e^{-\frac {kn} m}}]\\ &= (1 - e^{-\frac {kn} m})^k[ln(1 - e^{-\frac {kn} m}) +\frac {\frac {kn} m e^{-\frac {kn} m}} {1 - e^{-\frac {kn} m}}]\\ &=(1 - e^{-\frac {kn} m})^{k-1}[(1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) +\frac {kn} m e^{-\frac {kn} m}]\\ &=(1 - e^{-\frac {kn} m})^{k-1}[(1 - e^{-\frac {kn} m})ln(1 - e^{-\frac {kn} m}) -e^{-\frac {kn} m}lne^{-\frac {kn} m}]\\ 可以写成 &= (1 - e^{-\frac {kn} m})^{k-1}(ylny - xlnx)的形式 \\ \end{aligned}
f(k)f′(k)f(k)1f′(k)f′(k)可以写成=(1−e−mkn)k=0时,k=nmln2=ln(1−e−mkn)+k(ln(1−e−mkn))′=f(k)[ln(1−e−mkn)+1−e−mknmkne−mkn]=(1−e−mkn)k[ln(1−e−mkn)+1−e−mknmkne−mkn]=(1−e−mkn)k−1[(1−e−mkn)ln(1−e−mkn)+mkne−mkn]=(1−e−mkn)k−1[(1−e−mkn)ln(1−e−mkn)−e−mknlne−mkn]=(1−e−mkn)k−1(ylny−xlnx)的形式
(
1
)
首先讨论
(
1
−
e
−
k
n
m
)
k
−
1
的符号:
由最初
a
s
s
u
m
e
:
k
n
<
m
可得:
k
n
m
<
1
∈
(
0
,
1
)
−
k
n
m
∈
(
−
1
,
0
)
e
−
k
n
m
∈
(
e
−
1
,
e
0
)
,即
(
e
−
1
,
1
)
1
−
e
−
k
n
m
∈
(
0
,
1
−
e
−
1
)
(
1
−
e
−
k
n
m
)
k
−
1
>
0
\begin{aligned}(1)首先讨论&(1 - e^{-\frac {kn} m})^{k-1}的符号:\\ 由最初assume&:kn < m可得:\frac {kn} m < 1 ∈(0,1) \\ -\frac {kn} m &∈(-1,0) \\ e^{-\frac {kn} m}&∈(e^{-1},e^0),即(e^{-1},1) \\ 1 - e^{-\frac {kn} m}&∈(0,1-e^{-1})\\ (1 - e^{-\frac {kn} m})^{k-1} &> 0 \end{aligned}
(1)首先讨论由最初assume−mkne−mkn1−e−mkn(1−e−mkn)k−1(1−e−mkn)k−1的符号::kn<m可得:mkn<1∈(0,1)∈(−1,0)∈(e−1,e0),即(e−1,1)∈(0,1−e−1)>0
(
2
)
再讨论
(
y
l
n
y
−
x
l
n
x
)的符号:
k
<
m
n
l
n
2
时
:
k
n
m
<
l
n
2
−
k
n
m
>
−
l
n
2
,即
−
k
n
m
>
l
n
1
2
e
−
k
n
m
>
e
l
n
1
2
,即
e
−
k
n
m
>
1
2
,即
x
>
1
2
根据
x
下图图像可得:
y
l
n
y
−
x
l
n
x
<
0
此时
f
′
(
k
)
<
0
,
f
(
k
)
递减
↓
同理,
k
>
m
n
l
n
2
时
:
x
>
1
2
,
y
l
n
y
−
x
l
n
x
>
0
,
f
′
(
k
)
>
0
,
f
(
k
)
递增
↑
\begin{aligned} (2)再讨论&(ylny - xlnx)的符号:\\ k < \frac m nln2时&:\\ \frac {kn} m &< ln2\\ -\frac {kn} m &> -ln2,即-\frac {kn} m > ln\frac 1 2\\ e^{-\frac {kn} m} &> e^{ln \frac 1 2},即e^{-\frac {kn} m} > \frac1 2 ,即 x > \frac 1 2\\ 根据&x下图图像可得:ylny - xlnx <0\\ 此时&f'(k) < 0,f(k)递减↓\\ 同理,k > \frac m nln2时&:x>\frac1 2 ,ylny - xlnx >0,f'(k) > 0,f(k)递增↑ \end{aligned}
(2)再讨论k<nmln2时mkn−mkne−mkn根据此时同理,k>nmln2时(ylny−xlnx)的符号::<ln2>−ln2,即−mkn>ln21>eln21,即e−mkn>21,即x>21x下图图像可得:ylny−xlnx<0f′(k)<0,f(k)递减↓:x>21,ylny−xlnx>0,f′(k)>0,f(k)递增↑
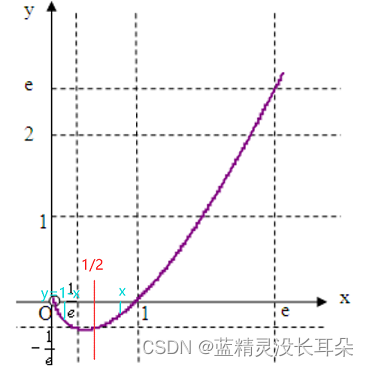
根据以上推理可得如下结论:
k
<
m
n
l
n
2
递减,
k
>
m
n
l
n
2
递增,在
k
=
m
n
l
n
2
处取得极小值(最小误判率)
k < \frac m nln2递减,k > \frac m nln2递增,在k=\frac m n ln2处取得极小值(最小误判率)
k<nmln2递减,k>nmln2递增,在k=nmln2处取得极小值(最小误判率)






















 30万+
30万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








